13.2作轴对称图形同步测试 2021-2022学年人教版八年级数学上册(第一课时 Word版 含答案)
文档属性
| 名称 | 13.2作轴对称图形同步测试 2021-2022学年人教版八年级数学上册(第一课时 Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 194.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 14:32:21 | ||
图片预览

文档简介
13.2
第1课时
画轴对称图形
同步测试
选择题
1.下列说法正确的是(
)
A.任何一个图形都有对称轴;
B.两个全等三角形一定关于某直线对称;
C.若△ABC与△A′B′C′成轴对称,则△ABC≌△A′B′C′;
D.点A,点B在直线1两旁,且AB与直线1交于点O,若AO=BO,则点A与点B关于直线l对称.
2.若在△ABC所在平面上求作一点P,使P到∠A的两边的距离相等,且PA=PB,那么下列确定P点的方法正确的是( )
A.P是∠A与∠B两角平分线的交点
B.P为AC、AB两边上的高的交点
C.P为∠A的角平分线与AB的垂直平分线的交点
D.P为∠A的角平分线与AB边上的中线的交点
3.如图,△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F为垂足,则下列四个结论,其中正确的个数是( )①∠DEF=∠DFE;②AE=AF;③AD垂直平分EF;④EF垂直平分AD.
1个
B.
2个
C.
3个
D.
4个
第3题
第5题
第6题
第7题
第8题
4.下列说法中,正确的是(
)
A.关于某直线对称的两个三角形是全等三角形
B.全等三角形是关于某直线对称的
C.两个图形关于某条直线对称,这两个图形一定分别位于这条直线的两侧
D.若点A、B关于直线MN对称,则AB垂直平分MN
5.如图,△ABC与△关于直线MN对称,P为MN上任一点,下列结论中错误的是(
)
A.△是等腰三角形
B.MN垂直平分,
C.△ABC与△面积相等
D.直线AB、的交点不一定在MN上
6.如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF
=150°,则∠AFE+∠BCD的大小是(
)
A.150°
B.300°
C.210°
D.330°
7.已知,为内一定点,上有一点,上有一点,当的周长取最小值时,的度数是
A.
B.
C.
D.
8.如图所示,在四边ABCD中,∠BAD=120°,∠B=∠D=90°,若在BC和CD上分别找一点M,使得△AMN的周长最小,则此时∠AMN+∠ANM的度数为(
)
A.110°
B.120°
C.140°
D.150°
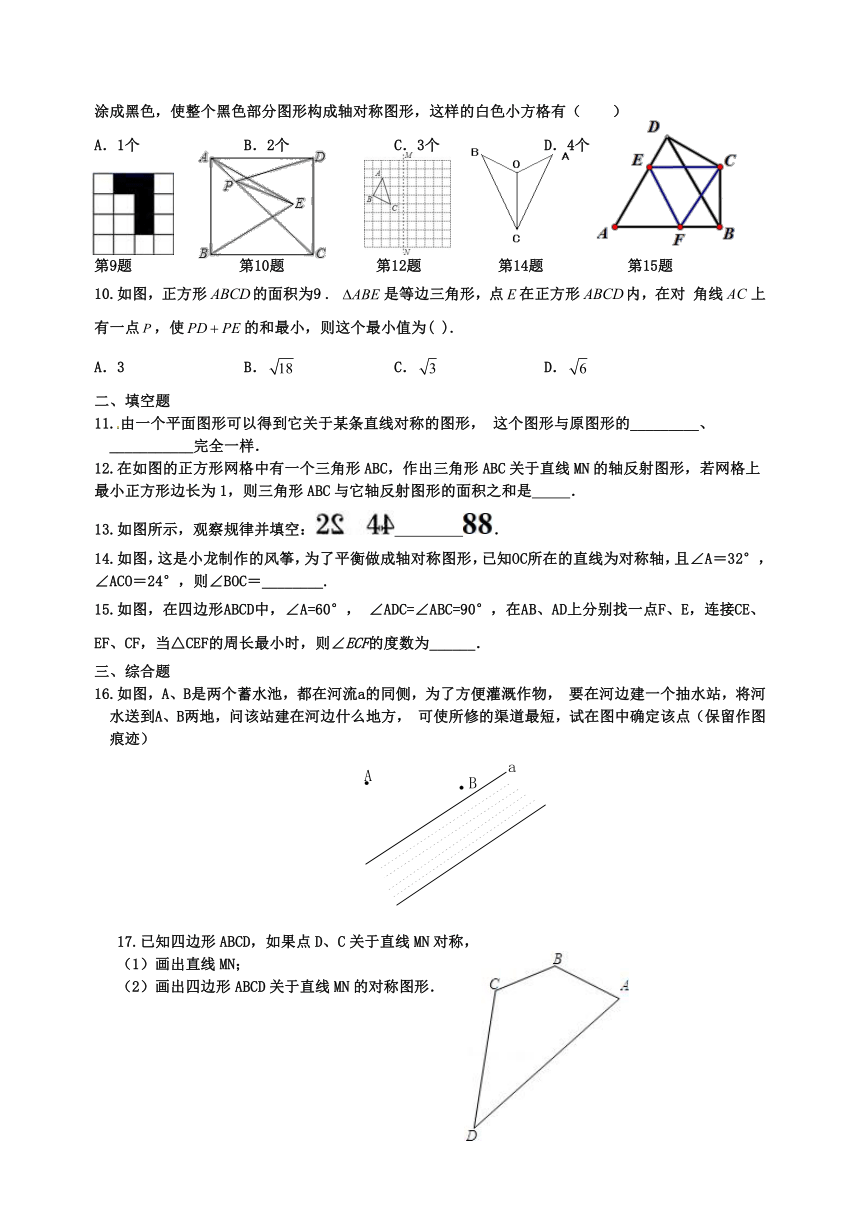
9.如图,是4×4正方形网格,其中已有4个小方格涂成了黑色.现在要从其余白色小方格中选出一个也涂成黑色,使整个黑色部分图形构成轴对称图形,这样的白色小方格有( )
A.1个
B.2个
C.3个
D.4个
第9题
第10题
第12题
第14题
第15题
10.如图,正方形的面积为9
.
是等边三角形,点在正方形内,在对
角线上有一点,使的和最小,则这个最小值为(
).
A.3
B.
C.
D.
填空题
11.由一个平面图形可以得到它关于某条直线对称的图形,这个图形与原图形的_________、___________完全一样.
12.在如图的正方形网格中有一个三角形ABC,作出三角形ABC关于直线MN的轴反射图形,若网格上最小正方形边长为1,则三角形ABC与它轴反射图形的面积之和是
.
13.如图所示,观察规律并填空:
.
14.如图,这是小龙制作的风筝,为了平衡做成轴对称图形,已知OC所在的直线为对称轴,且∠A=32°,
∠ACO=24°,则∠BOC=________.
15.如图,在四边形ABCD中,∠A=60°,
∠ADC=∠ABC=90°,在AB、AD上分别找一点F、E,连接CE、EF、CF,当△CEF的周长最小时,则∠ECF的度数为______.
综合题
16.如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点(保留作图痕迹)
17.已知四边形ABCD,如果点D、C关于直线MN对称,
(1)画出直线MN;
(2)画出四边形ABCD关于直线MN的对称图形.
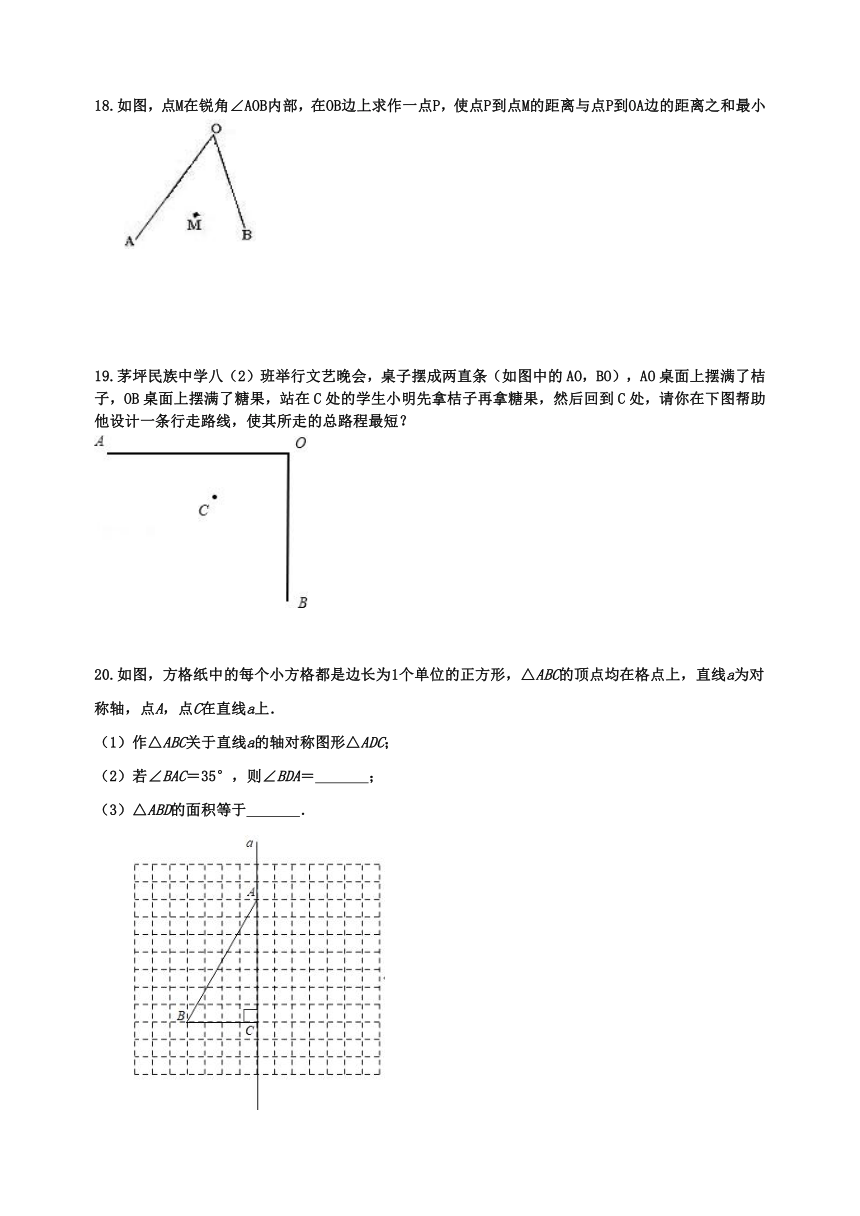
18.如图,点M在锐角∠AOB内部,在OB边上求作一点P,使点P到点M的距离与点P到OA边的距离之和最小
19.茅坪民族中学八(2)班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子,OB桌面上摆满了糖果,站在C处的学生小明先拿桔子再拿糖果,然后回到C处,请你在下图帮助他设计一条行走路线,使其所走的总路程最短?
20.如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上,直线a为对称轴,点A,点C在直线a上.
(1)作△ABC关于直线a的轴对称图形△ADC;
(2)若∠BAC=35°,则∠BDA=
;
(3)△ABD的面积等于
.
13.2
第1课时
画轴对称图形
同步测试答案
一、选择题
1.C
2.A
3.C
4.A
5.D
6.B
7.C
8.B
9.C
10.A
二、填空题
11.形状;大小
12.5.
.
13.
;.
14.124°
;
15.60°
三、综合题
16.解:作点A关于直线a对称的点C,连接BC交a于点P,则点P就是抽水站的位置
17.解:(1)如图,直线MN即为所求;
(2)四边形A′B′DC即为四边形ABDC关于直线MN的对称图形.
18.解:作法如下:
作M点关于OB的对称点,过作⊥于OA于H,交OB于P,点P为所求.
19.解:①分别作点C关于OA、OB的对称点是M、N,
②连接MN,分别交OA于D,OB于E.
则C→D→E→C为所求的行走路线.
20.解:(1)△ADC如图所示;
(2)∠BAD=2∠BAC=2×35°=70°,
∵AB=AD,
∴∠BDA=(180°-∠BAD)=55°;
故答案为:55°;
(3)△ABD的面积=×8×7=28,
故答案为:28.
第1课时
画轴对称图形
同步测试
选择题
1.下列说法正确的是(
)
A.任何一个图形都有对称轴;
B.两个全等三角形一定关于某直线对称;
C.若△ABC与△A′B′C′成轴对称,则△ABC≌△A′B′C′;
D.点A,点B在直线1两旁,且AB与直线1交于点O,若AO=BO,则点A与点B关于直线l对称.
2.若在△ABC所在平面上求作一点P,使P到∠A的两边的距离相等,且PA=PB,那么下列确定P点的方法正确的是( )
A.P是∠A与∠B两角平分线的交点
B.P为AC、AB两边上的高的交点
C.P为∠A的角平分线与AB的垂直平分线的交点
D.P为∠A的角平分线与AB边上的中线的交点
3.如图,△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F为垂足,则下列四个结论,其中正确的个数是( )①∠DEF=∠DFE;②AE=AF;③AD垂直平分EF;④EF垂直平分AD.
1个
B.
2个
C.
3个
D.
4个
第3题
第5题
第6题
第7题
第8题
4.下列说法中,正确的是(
)
A.关于某直线对称的两个三角形是全等三角形
B.全等三角形是关于某直线对称的
C.两个图形关于某条直线对称,这两个图形一定分别位于这条直线的两侧
D.若点A、B关于直线MN对称,则AB垂直平分MN
5.如图,△ABC与△关于直线MN对称,P为MN上任一点,下列结论中错误的是(
)
A.△是等腰三角形
B.MN垂直平分,
C.△ABC与△面积相等
D.直线AB、的交点不一定在MN上
6.如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF
=150°,则∠AFE+∠BCD的大小是(
)
A.150°
B.300°
C.210°
D.330°
7.已知,为内一定点,上有一点,上有一点,当的周长取最小值时,的度数是
A.
B.
C.
D.
8.如图所示,在四边ABCD中,∠BAD=120°,∠B=∠D=90°,若在BC和CD上分别找一点M,使得△AMN的周长最小,则此时∠AMN+∠ANM的度数为(
)
A.110°
B.120°
C.140°
D.150°
9.如图,是4×4正方形网格,其中已有4个小方格涂成了黑色.现在要从其余白色小方格中选出一个也涂成黑色,使整个黑色部分图形构成轴对称图形,这样的白色小方格有( )
A.1个
B.2个
C.3个
D.4个
第9题
第10题
第12题
第14题
第15题
10.如图,正方形的面积为9
.
是等边三角形,点在正方形内,在对
角线上有一点,使的和最小,则这个最小值为(
).
A.3
B.
C.
D.
填空题
11.由一个平面图形可以得到它关于某条直线对称的图形,这个图形与原图形的_________、___________完全一样.
12.在如图的正方形网格中有一个三角形ABC,作出三角形ABC关于直线MN的轴反射图形,若网格上最小正方形边长为1,则三角形ABC与它轴反射图形的面积之和是
.
13.如图所示,观察规律并填空:
.
14.如图,这是小龙制作的风筝,为了平衡做成轴对称图形,已知OC所在的直线为对称轴,且∠A=32°,
∠ACO=24°,则∠BOC=________.
15.如图,在四边形ABCD中,∠A=60°,
∠ADC=∠ABC=90°,在AB、AD上分别找一点F、E,连接CE、EF、CF,当△CEF的周长最小时,则∠ECF的度数为______.
综合题
16.如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点(保留作图痕迹)
17.已知四边形ABCD,如果点D、C关于直线MN对称,
(1)画出直线MN;
(2)画出四边形ABCD关于直线MN的对称图形.
18.如图,点M在锐角∠AOB内部,在OB边上求作一点P,使点P到点M的距离与点P到OA边的距离之和最小
19.茅坪民族中学八(2)班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子,OB桌面上摆满了糖果,站在C处的学生小明先拿桔子再拿糖果,然后回到C处,请你在下图帮助他设计一条行走路线,使其所走的总路程最短?
20.如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上,直线a为对称轴,点A,点C在直线a上.
(1)作△ABC关于直线a的轴对称图形△ADC;
(2)若∠BAC=35°,则∠BDA=
;
(3)△ABD的面积等于
.
13.2
第1课时
画轴对称图形
同步测试答案
一、选择题
1.C
2.A
3.C
4.A
5.D
6.B
7.C
8.B
9.C
10.A
二、填空题
11.形状;大小
12.5.
.
13.
;.
14.124°
;
15.60°
三、综合题
16.解:作点A关于直线a对称的点C,连接BC交a于点P,则点P就是抽水站的位置
17.解:(1)如图,直线MN即为所求;
(2)四边形A′B′DC即为四边形ABDC关于直线MN的对称图形.
18.解:作法如下:
作M点关于OB的对称点,过作⊥于OA于H,交OB于P,点P为所求.
19.解:①分别作点C关于OA、OB的对称点是M、N,
②连接MN,分别交OA于D,OB于E.
则C→D→E→C为所求的行走路线.
20.解:(1)△ADC如图所示;
(2)∠BAD=2∠BAC=2×35°=70°,
∵AB=AD,
∴∠BDA=(180°-∠BAD)=55°;
故答案为:55°;
(3)△ABD的面积=×8×7=28,
故答案为:28.
