溧水县第二高级中学数学教学案必修1:第16-17课时(函数单调性Ⅰ)(苏教版)
文档属性
| 名称 | 溧水县第二高级中学数学教学案必修1:第16-17课时(函数单调性Ⅰ)(苏教版) |

|
|
| 格式 | zip | ||
| 文件大小 | 711.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-23 16:58:23 | ||
图片预览

文档简介
总 课 题 函数概念与基本初等函数 分课时 第5、6课时 总课时 总第16、17课时
分 课 题 函数单调性(1) 课 型 新 授 课
教学目标 会运用图象判断单调性;理解函数的单调性,能判断或证明一些简单函数单调性;注意必须在定义域内或其子集内讨论函数的单调性。
重 点 函数单调性的证明及判断。
难 点 函数单调性证明及其应用。
一、复习引入
1、函数的定义域、值域、图象、表示方法
2、函数单调性
(1)单调增函数
(2)单调减函数
(3)单调区间
二、例题分析
例1、画出下列函数图象,并写出单调区间:
(1) (2) (2)
例2、求证:函数在区间上是单调增函数。
例3、讨论函数的单调性,并证明你的结论。
变(1)讨论函数的单调性,并证明你的结论
变(2)讨论函数的单调性,并证明你的结论。
例4、试判断函数在上的单调性。
三、随堂练习
1、判断下列说法正确的是 。
(1)若定义在上的函数满足,则函数是上的单调增函数;
(2)若定义在上的函数满足,则函数在上不是单调减函数;
(3)若定义在上的函数在区间上是单调增函数,在区间上也是单调增函数,则函数是上的单调增函数;
(4)若定义在上的函数在区间上是单调增函数,在区间上也是单调增函数,则函数是上的单调增函数。
2、若一次函数在上是单调减函数,则点在直角坐标平面的( )
A.上半平面 B.下半平面 C.左半平面 D.右半平面
3、函数在上是___ ___;函数在上是__ _____。
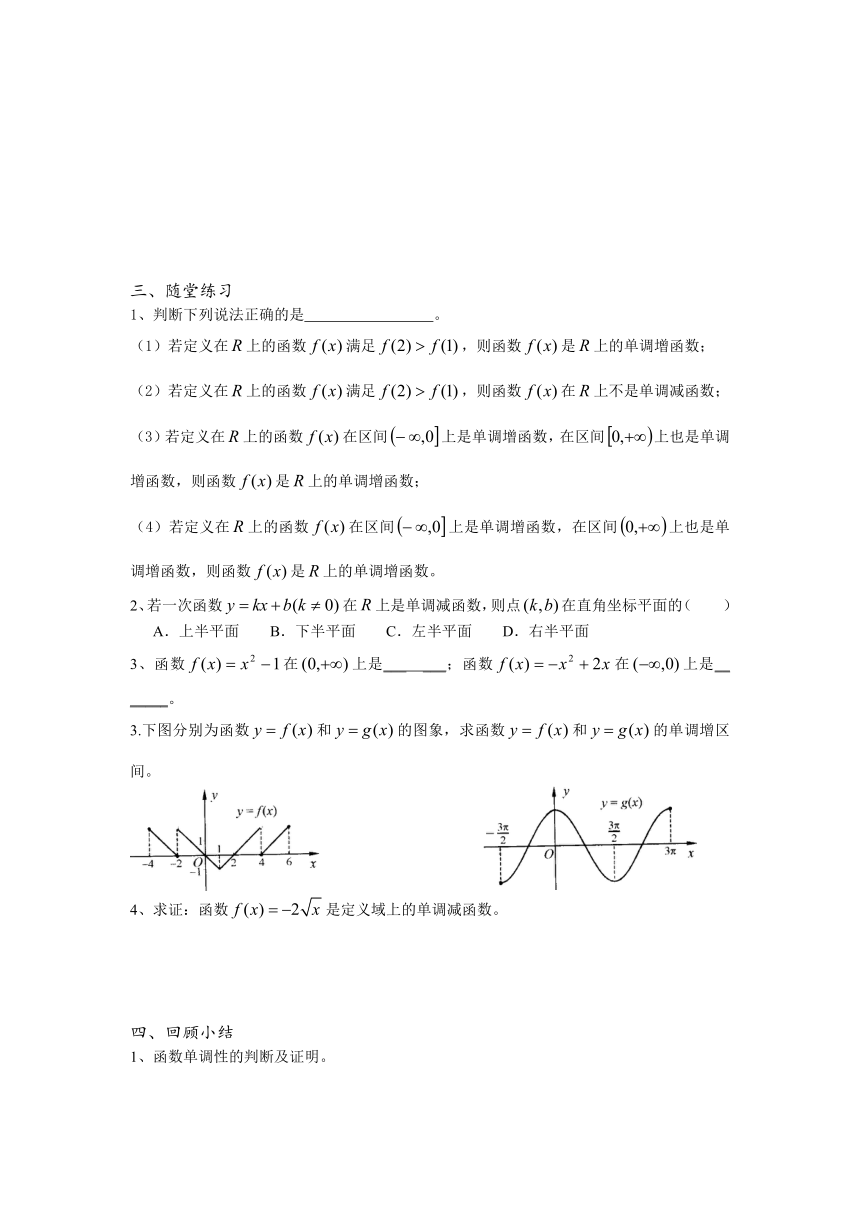
3.下图分别为函数和的图象,求函数和的单调增区间。
4、求证:函数是定义域上的单调减函数。
四、回顾小结
1、函数单调性的判断及证明。
课后作业
班级:高一( )班 姓名__________
一、基础题
1、求下列函数的单调区间
(1) (2)
(3) (4)=
2、画函数的图象,并写出单调区间。
二、提高题
3、求证:函数在上是单调增函数。
4、若函数,求函数的单调区间。
5、若函数在上是增函数,在上是减函数,试比较与的大小。
三、能力题
6、已知函数,试讨论函数f(x)在区间上的单调性。
变(1)已知函数,试讨论函数f(x)在区间上的单调性。
探究:函数的单调性。
得 分:____________________
批改时间:
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
分 课 题 函数单调性(1) 课 型 新 授 课
教学目标 会运用图象判断单调性;理解函数的单调性,能判断或证明一些简单函数单调性;注意必须在定义域内或其子集内讨论函数的单调性。
重 点 函数单调性的证明及判断。
难 点 函数单调性证明及其应用。
一、复习引入
1、函数的定义域、值域、图象、表示方法
2、函数单调性
(1)单调增函数
(2)单调减函数
(3)单调区间
二、例题分析
例1、画出下列函数图象,并写出单调区间:
(1) (2) (2)
例2、求证:函数在区间上是单调增函数。
例3、讨论函数的单调性,并证明你的结论。
变(1)讨论函数的单调性,并证明你的结论
变(2)讨论函数的单调性,并证明你的结论。
例4、试判断函数在上的单调性。
三、随堂练习
1、判断下列说法正确的是 。
(1)若定义在上的函数满足,则函数是上的单调增函数;
(2)若定义在上的函数满足,则函数在上不是单调减函数;
(3)若定义在上的函数在区间上是单调增函数,在区间上也是单调增函数,则函数是上的单调增函数;
(4)若定义在上的函数在区间上是单调增函数,在区间上也是单调增函数,则函数是上的单调增函数。
2、若一次函数在上是单调减函数,则点在直角坐标平面的( )
A.上半平面 B.下半平面 C.左半平面 D.右半平面
3、函数在上是___ ___;函数在上是__ _____。
3.下图分别为函数和的图象,求函数和的单调增区间。
4、求证:函数是定义域上的单调减函数。
四、回顾小结
1、函数单调性的判断及证明。
课后作业
班级:高一( )班 姓名__________
一、基础题
1、求下列函数的单调区间
(1) (2)
(3) (4)=
2、画函数的图象,并写出单调区间。
二、提高题
3、求证:函数在上是单调增函数。
4、若函数,求函数的单调区间。
5、若函数在上是增函数,在上是减函数,试比较与的大小。
三、能力题
6、已知函数,试讨论函数f(x)在区间上的单调性。
变(1)已知函数,试讨论函数f(x)在区间上的单调性。
探究:函数的单调性。
得 分:____________________
批改时间:
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
