人教版八年级数学上册12.3角平分线的性质课件(17张PPT)
文档属性
| 名称 | 人教版八年级数学上册12.3角平分线的性质课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 00:00:00 | ||
图片预览


文档简介
(共17张PPT)
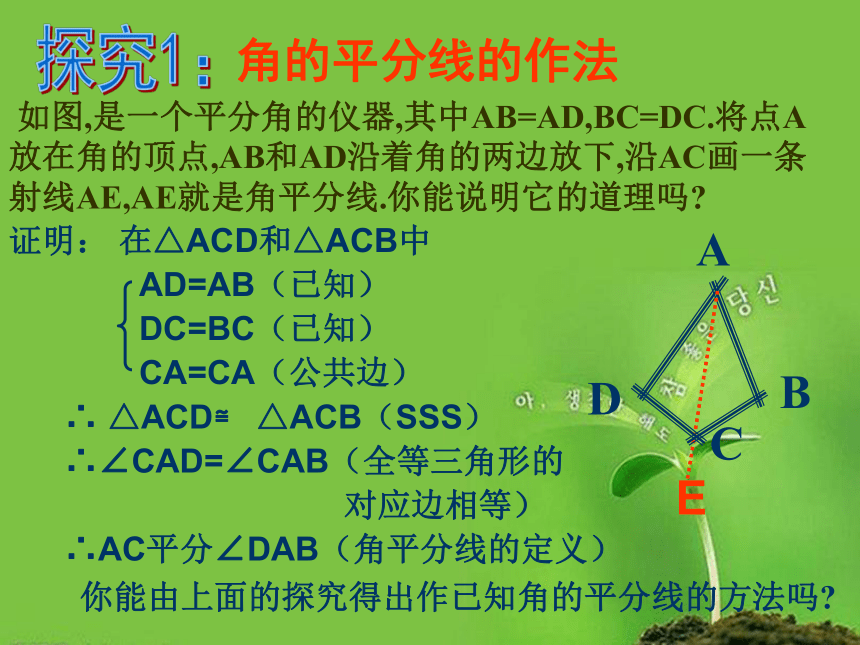
如图,是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线.你能说明它的道理吗?
C
A
D
B
你能由上面的探究得出作已知角的平分线的方法吗?
E
角的平分线的作法
证明:
在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∴
△ACD≌
△ACB(SSS)
∴∠CAD=∠CAB(全等三角形的
对应边相等)
∴AC平分∠DAB(角平分线的定义)
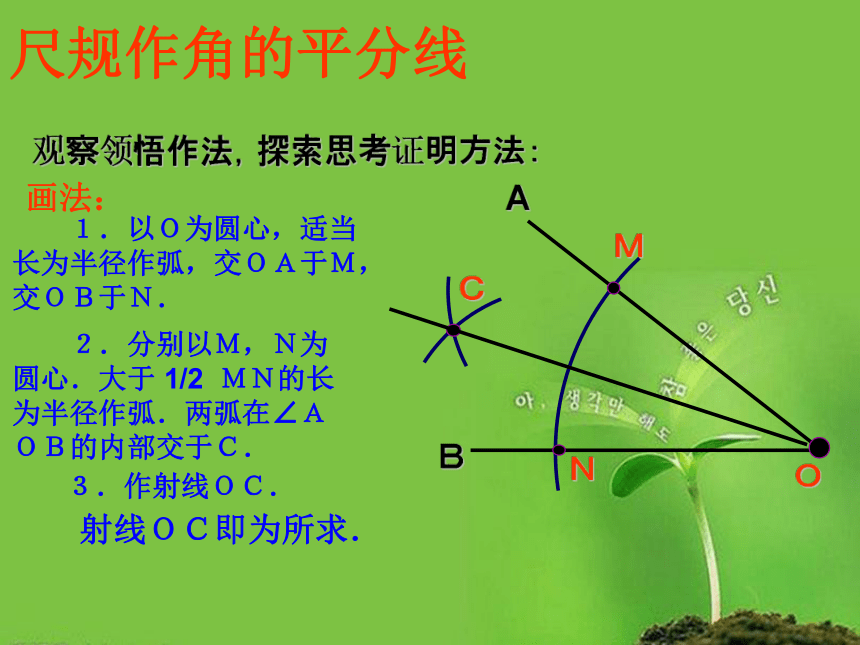
尺规作角的平分线
观察领悟作法,探索思考证明方法:
A
B
O
M
N
C
画法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
2.分别以M,N为圆心.大于
1/2
MN的长为半径作弧.两弧在∠AOB的内部交于C.
3.作射线OC.
射线OC即为所求.
A
B
M
N
C
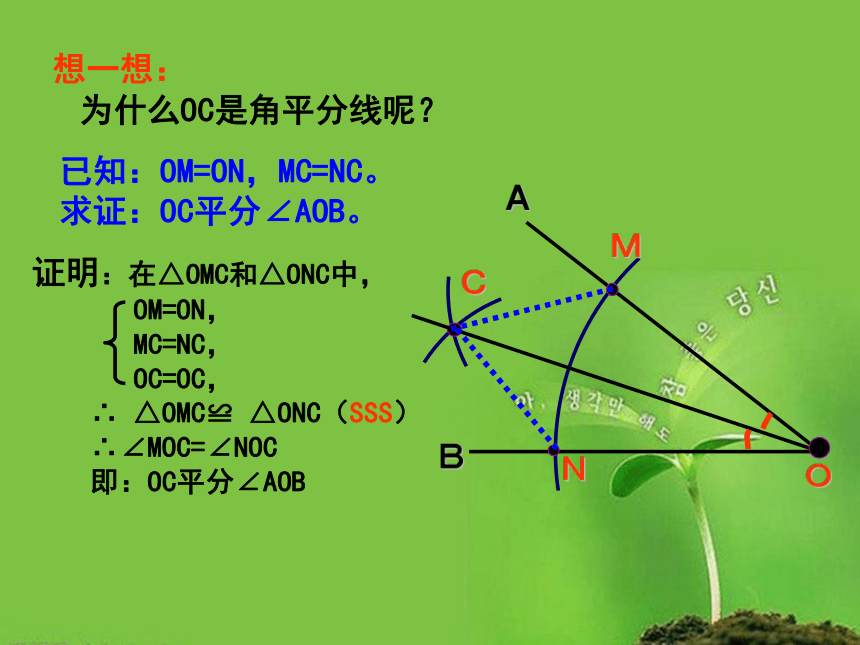
为什么OC是角平分线呢?
O
想一想:
已知:OM=ON,MC=NC。
求证:OC平分∠AOB。
证明:在△OMC和△ONC中,
OM=ON,
MC=NC,
OC=OC,
∴
△OMC≌
△ONC(SSS)
∴∠MOC=∠NOC
即:OC平分∠AOB
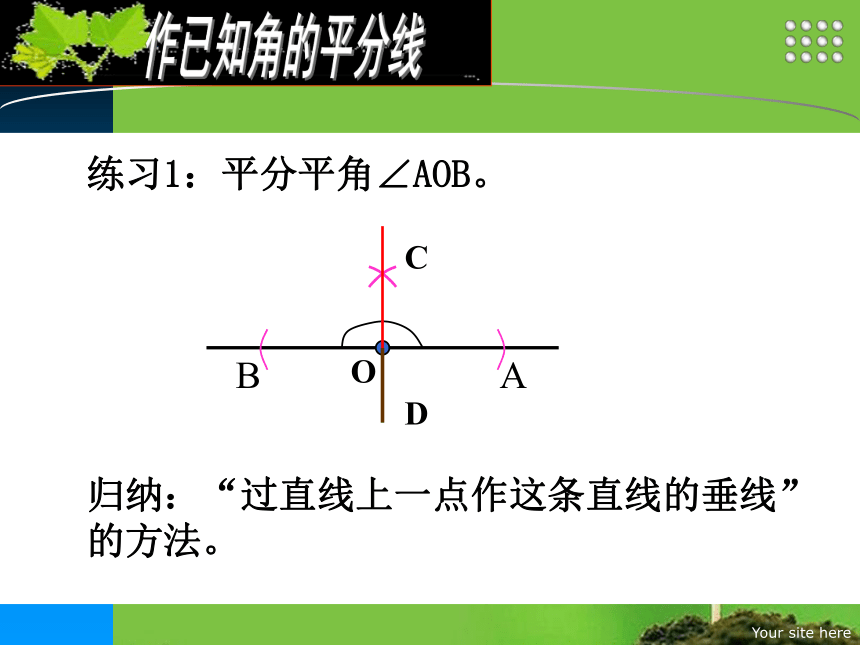
练习1:平分平角∠AOB。
归纳:“过直线上一点作这条直线的垂线”的方法。
A
B
O
C
D
A
B
O
A
O
E
B
C
P
D
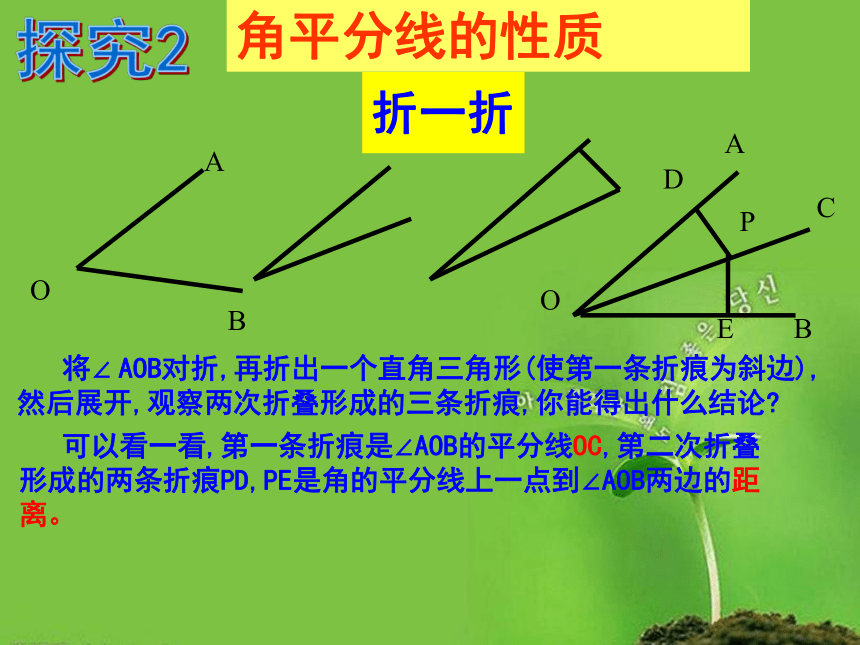
将∠
AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?
可以看一看,第一条折痕是∠AOB的平分线OC,第二次折叠形成的两条折痕PD,PE是角的平分线上一点到∠AOB两边的距离。
折一折
角平分线的性质
已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D,E。
求证:PD=PE
证明:∵
PD⊥OA,PE⊥OB(已知)
∴∠PDO=∠PEO=90(垂直的定义)
在△PDO和△PEO中
∴
PD=PE(全等三角形的对应边相等)
∠
PDO=
∠
PEO
∠
AOC=
∠
BOC
OP=OP
∴
△
PDO≌
△
PEO(AAS)
角的平分线上的点到这个角的两边的距离相等。
D
P
E
A
O
B
C
证明几何命题的一般步骤:
1、明确命题的已知和求证
2、根据题意,画出图形,并用数学符号表示已知和求证;
3、经过分析,找出由已知推出求证的途径,写出证明过程。
角平分线的性质
定理:角的平分线上的点到角的两边的距离相等
用符号语言表示为:
A
O
B
P
E
D
1
2
∵
∠1=
∠2
PD
⊥OA
,PE
⊥OB
∴PD=PE
(角的平分线上的点到角的两边的距离相等)
推理的理由有三个,必须写完全,不能少了任何一个。
角平分线的性质
角的平分线上的点到角的两边的距离相等。
B
A
D
O
P
E
C
定理应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离。
定理的作用:
证明线段相等。
∵
如图,AD平分∠BAC(已知)
∴
=
,(
)
在角的平分线上的点到这个角的两边的距离相等。
BD
CD
(×)
∵
如图,
DC⊥AC,DB⊥AB
(已知)
∴
=
,(
)
在角的平分线上的点到这个角的两边的距离相等。
BD
CD
(×)
∵
AD平分∠BAC,
DC⊥AC,DB⊥AB
(已知)
∴
=
,(
)
DB
DC
在角的平分线上的点到这个角的两边的距离相等。
√
不必再证全等
已知△ABC中,
∠C=900,AD平分∠
CAB,且
BC=8,BD=5,求点D到AB的距离是多少?
A
B
C
D
E
你会吗?
例
已知:如图,△ABC的角平分线BM、CN相交于点P.
求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD
、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE
(在角平分线上的点到角的两边的距离相等)
同理
PE=PF.
∴
PD=PE=PF.
即点P到边AB、BC、
CA的距离相等
A
B
C
M
N
P
D
E
F
◆这节课我们学习了哪些知识?
1、“作已知角的平分线”的尺规作图法;
2、角的平分线的性质:
111角的平分线上的点到角的两边的距离相等。
∵
OC是∠AOB的平分线,
又
PD⊥OA,PE⊥OB
∴
PD=PE
(角的平分线上的点
到角的两边距离相等).
E
D
O
A
B
P
C
几何语言:
3、角的平分线的判定:
到角的两边的距离相等的点在角的平分线上。
∵
PD⊥OA,PE⊥OB
又PD=PE
∴
OC是∠AOB的平分线
(角的平分线上的点到角的两边距离相等).
E
D
O
A
B
P
C
几何语言:
如图,是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线.你能说明它的道理吗?
C
A
D
B
你能由上面的探究得出作已知角的平分线的方法吗?
E
角的平分线的作法
证明:
在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∴
△ACD≌
△ACB(SSS)
∴∠CAD=∠CAB(全等三角形的
对应边相等)
∴AC平分∠DAB(角平分线的定义)
尺规作角的平分线
观察领悟作法,探索思考证明方法:
A
B
O
M
N
C
画法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
2.分别以M,N为圆心.大于
1/2
MN的长为半径作弧.两弧在∠AOB的内部交于C.
3.作射线OC.
射线OC即为所求.
A
B
M
N
C
为什么OC是角平分线呢?
O
想一想:
已知:OM=ON,MC=NC。
求证:OC平分∠AOB。
证明:在△OMC和△ONC中,
OM=ON,
MC=NC,
OC=OC,
∴
△OMC≌
△ONC(SSS)
∴∠MOC=∠NOC
即:OC平分∠AOB
练习1:平分平角∠AOB。
归纳:“过直线上一点作这条直线的垂线”的方法。
A
B
O
C
D
A
B
O
A
O
E
B
C
P
D
将∠
AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?
可以看一看,第一条折痕是∠AOB的平分线OC,第二次折叠形成的两条折痕PD,PE是角的平分线上一点到∠AOB两边的距离。
折一折
角平分线的性质
已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D,E。
求证:PD=PE
证明:∵
PD⊥OA,PE⊥OB(已知)
∴∠PDO=∠PEO=90(垂直的定义)
在△PDO和△PEO中
∴
PD=PE(全等三角形的对应边相等)
∠
PDO=
∠
PEO
∠
AOC=
∠
BOC
OP=OP
∴
△
PDO≌
△
PEO(AAS)
角的平分线上的点到这个角的两边的距离相等。
D
P
E
A
O
B
C
证明几何命题的一般步骤:
1、明确命题的已知和求证
2、根据题意,画出图形,并用数学符号表示已知和求证;
3、经过分析,找出由已知推出求证的途径,写出证明过程。
角平分线的性质
定理:角的平分线上的点到角的两边的距离相等
用符号语言表示为:
A
O
B
P
E
D
1
2
∵
∠1=
∠2
PD
⊥OA
,PE
⊥OB
∴PD=PE
(角的平分线上的点到角的两边的距离相等)
推理的理由有三个,必须写完全,不能少了任何一个。
角平分线的性质
角的平分线上的点到角的两边的距离相等。
B
A
D
O
P
E
C
定理应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离。
定理的作用:
证明线段相等。
∵
如图,AD平分∠BAC(已知)
∴
=
,(
)
在角的平分线上的点到这个角的两边的距离相等。
BD
CD
(×)
∵
如图,
DC⊥AC,DB⊥AB
(已知)
∴
=
,(
)
在角的平分线上的点到这个角的两边的距离相等。
BD
CD
(×)
∵
AD平分∠BAC,
DC⊥AC,DB⊥AB
(已知)
∴
=
,(
)
DB
DC
在角的平分线上的点到这个角的两边的距离相等。
√
不必再证全等
已知△ABC中,
∠C=900,AD平分∠
CAB,且
BC=8,BD=5,求点D到AB的距离是多少?
A
B
C
D
E
你会吗?
例
已知:如图,△ABC的角平分线BM、CN相交于点P.
求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD
、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE
(在角平分线上的点到角的两边的距离相等)
同理
PE=PF.
∴
PD=PE=PF.
即点P到边AB、BC、
CA的距离相等
A
B
C
M
N
P
D
E
F
◆这节课我们学习了哪些知识?
1、“作已知角的平分线”的尺规作图法;
2、角的平分线的性质:
111角的平分线上的点到角的两边的距离相等。
∵
OC是∠AOB的平分线,
又
PD⊥OA,PE⊥OB
∴
PD=PE
(角的平分线上的点
到角的两边距离相等).
E
D
O
A
B
P
C
几何语言:
3、角的平分线的判定:
到角的两边的距离相等的点在角的平分线上。
∵
PD⊥OA,PE⊥OB
又PD=PE
∴
OC是∠AOB的平分线
(角的平分线上的点到角的两边距离相等).
E
D
O
A
B
P
C
几何语言:
