人教版八年级数学上册13.3.1等腰三角形的判定 课件(共16张PPT)
文档属性
| 名称 | 人教版八年级数学上册13.3.1等腰三角形的判定 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 00:00:00 | ||
图片预览

文档简介
(共16张PPT)
13.3.1
等腰三角形的判定
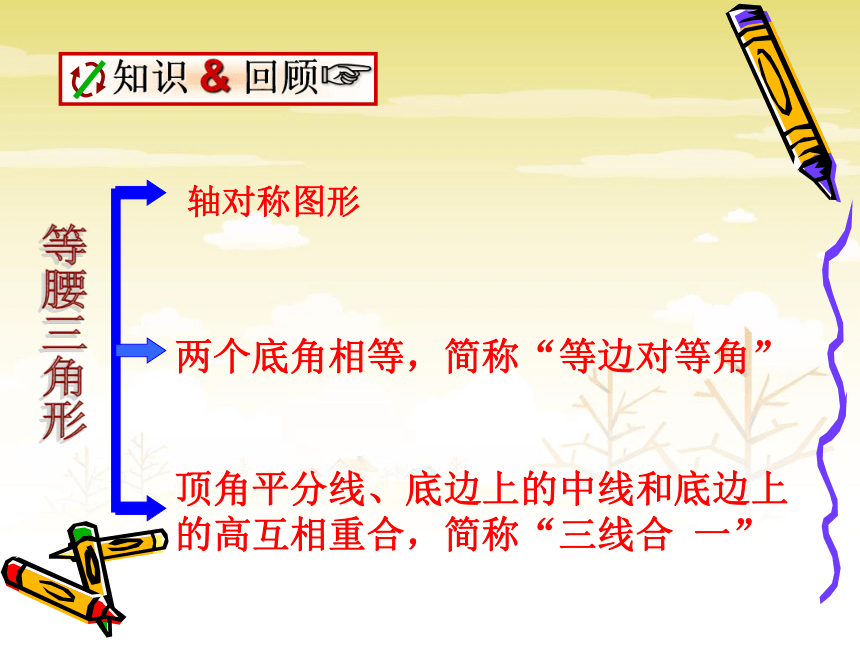
轴对称图形
两个底角相等,简称“等边对等角”
顶角平分线、底边上的中线和底边上的高互相重合,简称“三线合
一”
知识
&
回顾
?
A
B
O
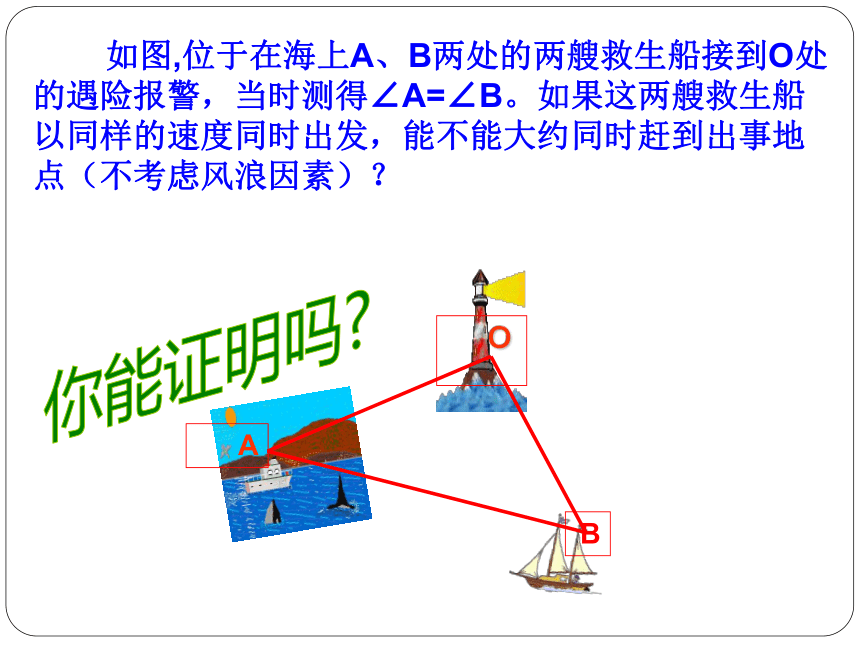
如图,位于在海上A、B两处的两艘救生船接到O处的遇险报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
A
B
O
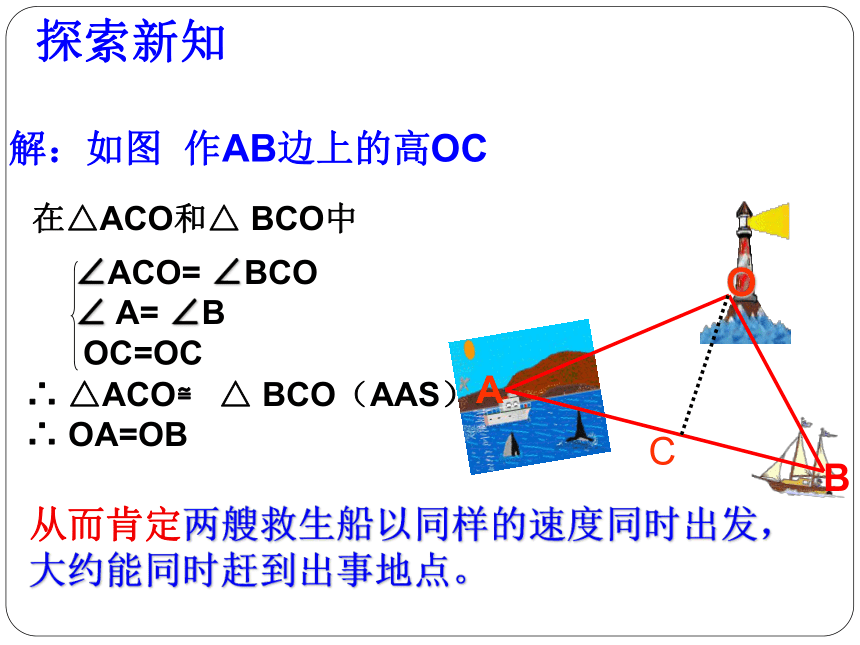
探索新知
解:如图
作AB边上的高OC
C
∠ACO=
∠BCO
∠
A=
∠B
OC=OC
从而肯定两艘救生船以同样的速度同时出发,
大约能同时赶到出事地点。
在△ACO和△
BCO中
∴
△ACO≌
△
BCO(AAS)
∴
OA=OB
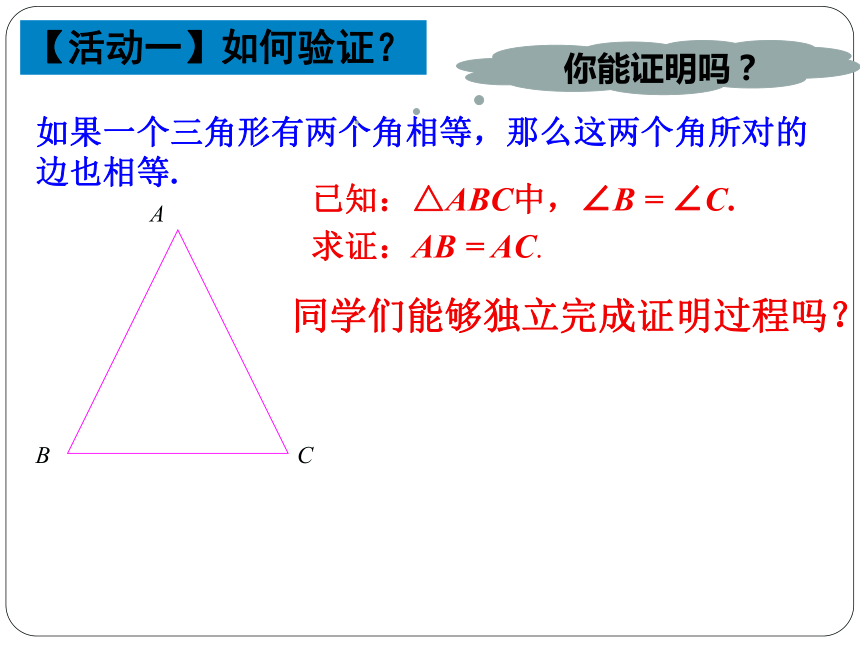
如果一个三角形有两个角相等,那么这两个角所对的边也相等.
你能证明吗?
A
B
C
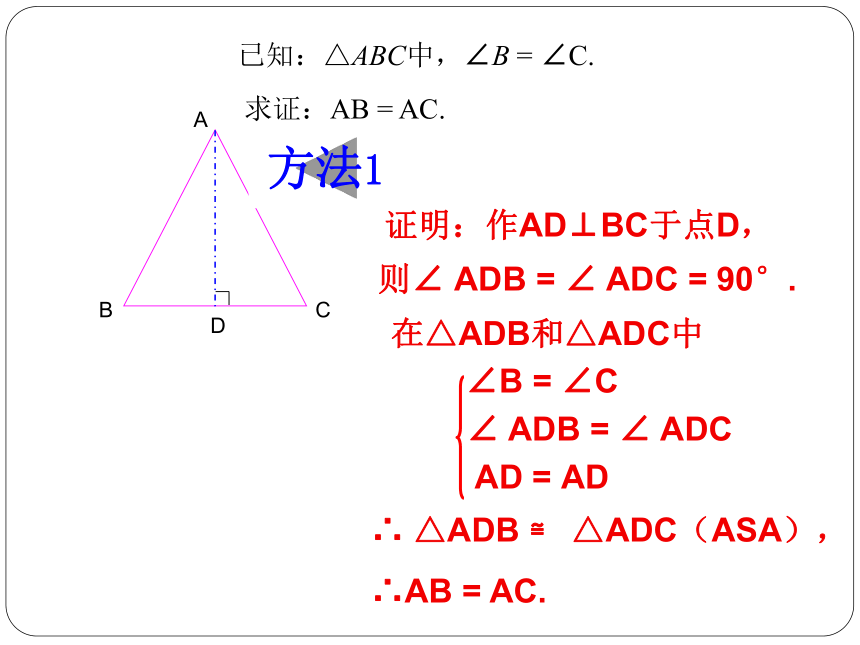
已知:△ABC中,∠B
=
∠C.
求证:AB
=
AC.
同学们能够独立完成证明过程吗?
【活动一】如何验证?
A
B
C
已知:△ABC中,∠B
=
∠C.
求证:AB
=
AC.
D
∠B
=
∠C
∠
ADB
=
∠
ADC
AD
=
AD
方法1
证明:作AD⊥BC于点D,
则∠
ADB
=
∠
ADC
=
90°.
在△ADB和△ADC中
∴
△ADB
≌
△ADC(ASA),
∴AB
=
AC.
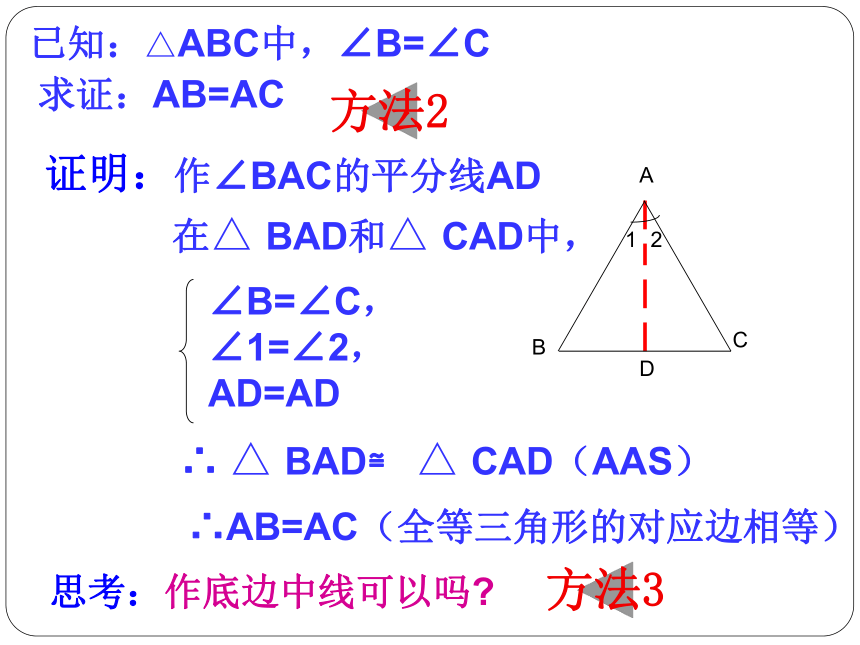
已知:△ABC中,∠B=∠C
求证:AB=AC
证明:
作∠BAC的平分线AD
在△
BAD和△
CAD中,
∠B=∠C,
∠1=∠2,
AD=AD
∴
△
BAD≌
△
CAD(AAS)
∴AB=AC(全等三角形的对应边相等)
1
A
B
C
D
2
思考:作底边中线可以吗?
方法2
方法3
等腰三角形的判定定理
如果一个三角形有两个角相等,那么这个三角形是等腰三角形。
简写成:等角对等边
等腰三角形的性质定理和判定定理
互为逆命题
等腰三角形的性质与判定的区别
性质是:等边
等角
判定是:等角
等边
求证:如果三角形一个外角的平分线平行于三角形的一边,
那么这个三角形是等腰三角形.
A
B
C
E
D
已知:如图,
∠CAE
是△ABC
的一个外角,AD平分∠CAE,且AD∥BC.
求证:△ABC是等腰三角形.
证明:∵
AD平分∠CAE,
∴ ∠
DAE
=
∠DAC.
∵
AD∥BC,
∴ ∠DAE=∠B,∠DAC=
∠C,
∴ ∠B
=
∠C,
∴ AB
=
AC,
∴ △ABC是等腰三角形.
【活动二】应用举例,变式练习
例3
已知等腰三角形底边长为a,底边上的高的长为b,求作这个等腰三角形。
a
b
作法:
(1)作线段AB=a
(2)作线段AB的垂直平分线MN,与AB相交于点D。
(3)在MN上取一点C,使DC=h
(4)连接AC,BC,则△ABC就是所求作的等腰三角形
C
A
B
N
M
D
2、等腰三角形的判定方法有下列几种:
3、等腰三角形的判定定理与性质定理的区别是
。
4、运用等腰三角形的判定定理时,应注意
。
①定义,②判定定理
条件和结论刚好相反。
在同一个三角形中
1、等腰三角形的判定定理及其推论的内容是什么?
小结
名称
图
形
概
念
性质与边角关系
判
定
等
腰
三
角
形
A
B
C
有两边相等的三角形是等腰三角形。
2.等边对等角,
3.
三线合一。
4.是轴对称图形.
2.等角对等边,
1.两边相等。
1.两腰相等.
练习1
已知:如图∠A=360,∠DBC
=360,
∠C=720。计算∠1和∠2,并说明图中有哪些等腰三角形?
C
B
A
D
1
2
解:
∠1=720
∠2=360
等腰三角形有:
△
ABC,
△
ABD,
△
BCD
练习2
如图,把一张矩形的纸沿对角线折叠,
重合的部分是一个等腰三角形吗?为什么?
A
B
C
G
D
E
1
2
3
解:重合部分是等腰三角形。
理由:由ABDC是矩形知
AC∥BD
∴∠
3=
∠
2
由沿对角线折叠知∠
1
=
∠
2
∴
∠
1=
∠
3
∴
BG=GC(等角对等边)
【活动三】课堂练习,拓展引申
(1)根据下列条件指出各个图形中哪个三角形是等腰三角形?
A
B
C
D
E
①如图,BD平分∠ABC,DE∥BC.
②如图,AD平分∠BAC,CE∥AD;
③如图,AO、BO是三角形ABC的角平分线,
DE经过点O且DE∥AB;
变式1:AE、BD、DE三线段有何关系?
变式2:若AC=AB,则图中有哪几个等腰三角形
如图,AB=AC,BD平分∠ABC,CD平分∠ACB,EF∥BC.
(1)图中有几个等腰三角形?
(2)若△ABC中没有两边相等,则线段EF、线段BE、CF有何数量关系?
(3)若过△ABC的一个内角平分线和一个外角平分线的交点作这两角的公共边的平行线,如图,则EF、BE、CF之间有何数量关系?
13.3.1
等腰三角形的判定
轴对称图形
两个底角相等,简称“等边对等角”
顶角平分线、底边上的中线和底边上的高互相重合,简称“三线合
一”
知识
&
回顾
?
A
B
O
如图,位于在海上A、B两处的两艘救生船接到O处的遇险报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
A
B
O
探索新知
解:如图
作AB边上的高OC
C
∠ACO=
∠BCO
∠
A=
∠B
OC=OC
从而肯定两艘救生船以同样的速度同时出发,
大约能同时赶到出事地点。
在△ACO和△
BCO中
∴
△ACO≌
△
BCO(AAS)
∴
OA=OB
如果一个三角形有两个角相等,那么这两个角所对的边也相等.
你能证明吗?
A
B
C
已知:△ABC中,∠B
=
∠C.
求证:AB
=
AC.
同学们能够独立完成证明过程吗?
【活动一】如何验证?
A
B
C
已知:△ABC中,∠B
=
∠C.
求证:AB
=
AC.
D
∠B
=
∠C
∠
ADB
=
∠
ADC
AD
=
AD
方法1
证明:作AD⊥BC于点D,
则∠
ADB
=
∠
ADC
=
90°.
在△ADB和△ADC中
∴
△ADB
≌
△ADC(ASA),
∴AB
=
AC.
已知:△ABC中,∠B=∠C
求证:AB=AC
证明:
作∠BAC的平分线AD
在△
BAD和△
CAD中,
∠B=∠C,
∠1=∠2,
AD=AD
∴
△
BAD≌
△
CAD(AAS)
∴AB=AC(全等三角形的对应边相等)
1
A
B
C
D
2
思考:作底边中线可以吗?
方法2
方法3
等腰三角形的判定定理
如果一个三角形有两个角相等,那么这个三角形是等腰三角形。
简写成:等角对等边
等腰三角形的性质定理和判定定理
互为逆命题
等腰三角形的性质与判定的区别
性质是:等边
等角
判定是:等角
等边
求证:如果三角形一个外角的平分线平行于三角形的一边,
那么这个三角形是等腰三角形.
A
B
C
E
D
已知:如图,
∠CAE
是△ABC
的一个外角,AD平分∠CAE,且AD∥BC.
求证:△ABC是等腰三角形.
证明:∵
AD平分∠CAE,
∴ ∠
DAE
=
∠DAC.
∵
AD∥BC,
∴ ∠DAE=∠B,∠DAC=
∠C,
∴ ∠B
=
∠C,
∴ AB
=
AC,
∴ △ABC是等腰三角形.
【活动二】应用举例,变式练习
例3
已知等腰三角形底边长为a,底边上的高的长为b,求作这个等腰三角形。
a
b
作法:
(1)作线段AB=a
(2)作线段AB的垂直平分线MN,与AB相交于点D。
(3)在MN上取一点C,使DC=h
(4)连接AC,BC,则△ABC就是所求作的等腰三角形
C
A
B
N
M
D
2、等腰三角形的判定方法有下列几种:
3、等腰三角形的判定定理与性质定理的区别是
。
4、运用等腰三角形的判定定理时,应注意
。
①定义,②判定定理
条件和结论刚好相反。
在同一个三角形中
1、等腰三角形的判定定理及其推论的内容是什么?
小结
名称
图
形
概
念
性质与边角关系
判
定
等
腰
三
角
形
A
B
C
有两边相等的三角形是等腰三角形。
2.等边对等角,
3.
三线合一。
4.是轴对称图形.
2.等角对等边,
1.两边相等。
1.两腰相等.
练习1
已知:如图∠A=360,∠DBC
=360,
∠C=720。计算∠1和∠2,并说明图中有哪些等腰三角形?
C
B
A
D
1
2
解:
∠1=720
∠2=360
等腰三角形有:
△
ABC,
△
ABD,
△
BCD
练习2
如图,把一张矩形的纸沿对角线折叠,
重合的部分是一个等腰三角形吗?为什么?
A
B
C
G
D
E
1
2
3
解:重合部分是等腰三角形。
理由:由ABDC是矩形知
AC∥BD
∴∠
3=
∠
2
由沿对角线折叠知∠
1
=
∠
2
∴
∠
1=
∠
3
∴
BG=GC(等角对等边)
【活动三】课堂练习,拓展引申
(1)根据下列条件指出各个图形中哪个三角形是等腰三角形?
A
B
C
D
E
①如图,BD平分∠ABC,DE∥BC.
②如图,AD平分∠BAC,CE∥AD;
③如图,AO、BO是三角形ABC的角平分线,
DE经过点O且DE∥AB;
变式1:AE、BD、DE三线段有何关系?
变式2:若AC=AB,则图中有哪几个等腰三角形
如图,AB=AC,BD平分∠ABC,CD平分∠ACB,EF∥BC.
(1)图中有几个等腰三角形?
(2)若△ABC中没有两边相等,则线段EF、线段BE、CF有何数量关系?
(3)若过△ABC的一个内角平分线和一个外角平分线的交点作这两角的公共边的平行线,如图,则EF、BE、CF之间有何数量关系?
