山东省淄博市高青县(五四制)2020-2021学年六年级下学期期末考试数学试题(Word版 含解析)
文档属性
| 名称 | 山东省淄博市高青县(五四制)2020-2021学年六年级下学期期末考试数学试题(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 446.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 12:11:54 | ||
图片预览




文档简介
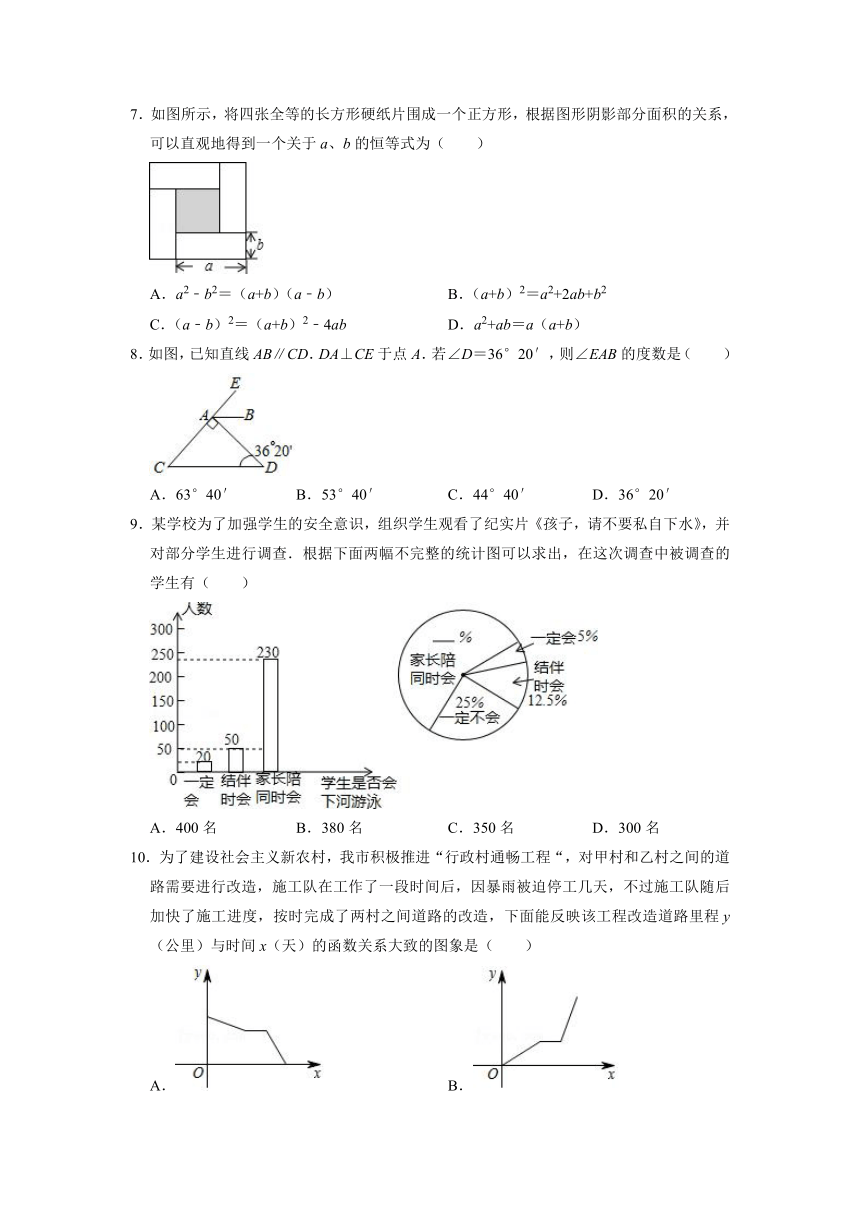
2020-2021学年山东省淄博市高青县六年级(下)期末数学试卷(五四学制)
一、选择题(本题有12小题,每小题5分,共60分,每小题只有一个选项是正确的,不选、多选、错选,均不得分)
1.如图,能用∠AOB,∠O,∠1三种方法表示同一个角的图形是( )
A.
B.
C.
D.
2.下列计算正确的是( )
A.a3﹣a2=a
B.a6÷a2=a3
C.a6﹣a2=a4
D.a3÷a2=a
3.根据语句“直线l1与直线l2相交,点M在直线l1上,直线l2不经过点M.”画出的图形是( )
A.
B.
C.
D.
4.下列调查中,适宜用普查方式的是( )
A.了解一批袋装食品是否含有防腐剂
B.了解一批灯泡的使用寿命
C.了解中央电视台新闻联播的收视率
D.了解某班学生“50m跑”的成绩
5.把一个长为5,宽为2的长方形的长减少x(0≤x<5),宽不变,所得长方形的面积y关于x的函数表达式为( )
A.y=﹣2x+10
B.y=5x
C.y=2x
D.y=10﹣x
6.两根木条,一根长10cm,另一根长12cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A.1cm
B.11cm
C.1cm
或11cm
D.2cm或11cm
7.如图所示,将四张全等的长方形硬纸片围成一个正方形,根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为( )
A.a2﹣b2=(a+b)(a﹣b)
B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=(a+b)2﹣4ab
D.a2+ab=a(a+b)
8.如图,已知直线AB∥CD.DA⊥CE于点A.若∠D=36°20′,则∠EAB的度数是( )
A.63°40′
B.53°40′
C.44°40′
D.36°20′
9.某学校为了加强学生的安全意识,组织学生观看了纪实片《孩子,请不要私自下水》,并对部分学生进行调查.根据下面两幅不完整的统计图可以求出,在这次调查中被调查的学生有( )
A.400名
B.380名
C.350名
D.300名
10.为了建设社会主义新农村,我市积极推进“行政村通畅工程“,对甲村和乙村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,不过施工队随后加快了施工进度,按时完成了两村之间道路的改造,下面能反映该工程改造道路里程y(公里)与时间x(天)的函数关系大致的图象是( )
A.
B.
C.
D.
11.有一个长方形内部剪掉了一个小长方形,它们的尺寸如图所示,则余下的部分(阴影部分)的面积( )
A.4a2
B.4a2﹣ab
C.4a2+ab
D.4a2﹣ab﹣2b2
12.在同一平面内,若∠A与∠B的两边分别平行,且∠A比∠B的3倍少40°,则∠A的度数为( )
A.20°
B.55°
C.20°或125°
D.20°或55°
二、填空题(共5小题,每小题4分,满分20分)
13.(4分)如图,点O在直线AE上,射线OC平分∠AOE.如果∠DOB=90°,∠1=25°,那么∠AOB的度数为
.
14.(4分)已知10a=2,10b=3,则102a+3b=
.
15.(4分)小鸡孵化场孵化出一批小鸡,工人在其中50只小鸡上做记号后让这批小鸡充分跑散,后来再任意抓出100只小鸡,其中有记号的有10只,则这批小鸡大约有
只.
16.(4分)某市出租车白天的收费起步价为7元,即路程不超过3千米时收费7元,超过部分每千米收费1.2元,如果乘客白天乘坐出租车的路程为x(x>3)千米,乘车费为y元,那么y与x之间的关系为
.
17.(4分)如图,已知AB∥CD,则∠A、∠C、∠P的关系为
.
三、解答题(共7小题,共70分)
18.(8分)化简:
(1)2(2x2﹣xy)+x(x﹣y);
(2)ab(2ab2﹣a2b)﹣(2ab)2b+a3b2.
19.(8分)如图,点B是线段AC上一点,且AB=21cm,BC=AB.
(1)试求出线段AC的长;
(2)如果点O是线段AC的中点,请求线段OB的长.
20.(10分)某校进行“垃圾分一分,环境美十分”的主题宣传活动,随机调查了部分学生对垃圾分类知识的了解情况.调查选项分为“A:非常了解,B:比较了解,C:基本了解,D:不了解”四种,并将调查结果绘制成如图两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
(1)把两幅统计图补充完整;
(2)本次调查了
名学生;
(3)根据上述调查数据,请你提出一条合理化建议
.
21.(10分)“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)小明在书店停留了多少分钟?
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
(4)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
22.(10分)如图,AC∥FE,∠1+∠3=180°.
(1)判定∠FAB与∠4的大小关系,并说明理由;
(2)若AC平分∠FAB,EF⊥BE于点E,∠4=78°,求∠BCD的度数.
23.(12分)如图1,将一个长为4a,宽为2b的长方形,沿图中虚线均匀分成4个小长方形,然后按图2形状拼成一个正方形.
(1)图2的空白部分的边长是多少?(用含a、b的式子表示)
(2)若2a+b=7,且ab=3,求图2中的空白正方形的面积.
(3)观察图2,用等式表示出(2a﹣b)2,ab和(2a+b)2的数量关系.
24.(12分)如图,AB∥CD,∠ABE=120°.
(1)如图①,写出∠BED与∠D的数量关系,并证明你的结论;
(2)如图②,∠DEF=2∠BEF,∠CDF=∠CDE,EF与DF交于点F,求∠EFD的度数;
(3)如图③,过B作BG⊥AB于G点,∠CDE=4∠GDE,求的值.
2020-2021学年山东省淄博市高青县六年级(下)期末数学试卷(五四学制)
参考答案与试题解析
一、选择题(本题有12小题,每小题5分,共60分,每小题只有一个选项是正确的,不选、多选、错选,均不得分)
1.如图,能用∠AOB,∠O,∠1三种方法表示同一个角的图形是( )
A.
B.
C.
D.
【分析】直接利用角的概念分析得出答案.
【解答】解:A、∠O无法表示一个角,故此选项不合题意;
B、∠AOB,∠O,∠1三种方法表示同一个角的图形,符合题意;
C、∠O无法表示一个角,故此选项不合题意;
D、∠O无法表示一个角,故此选项不合题意;
故选:B.
2.下列计算正确的是( )
A.a3﹣a2=a
B.a6÷a2=a3
C.a6﹣a2=a4
D.a3÷a2=a
【分析】直接利用合并同类项法则以及同底数幂的除法运算法则分别计算得出答案.
【解答】解:A、a3﹣a2无法计算,故此选项错误;
B、a6÷a2=a4,故此选项错误;
C、a6﹣a2无法计算,故此选项错误;
D、a3÷a2=a,故此选项正确.
故选:D.
3.根据语句“直线l1与直线l2相交,点M在直线l1上,直线l2不经过点M.”画出的图形是( )
A.
B.
C.
D.
【分析】根据直线l1与直线l2相交,点M在直线l1上,直线l2不经过点M进行判断,即可得出结论.
【解答】解:A.直线l2不经过点M,故本选项不合题意;
B.点M在直线l1上,故本选项不合题意;
C.点M在直线l1上,故本选项不合题意;
D.直线l1与直线l2相交,点M在直线l1上,直线l2不经过点M,故本选项符合题意;
故选:D.
4.下列调查中,适宜用普查方式的是( )
A.了解一批袋装食品是否含有防腐剂
B.了解一批灯泡的使用寿命
C.了解中央电视台新闻联播的收视率
D.了解某班学生“50m跑”的成绩
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
【解答】解:A、了解一批袋装食品是否含有防腐剂,适宜用抽样调查方式;
B、了解一批灯泡的使用寿命,适宜用抽样调查方式;
C、了解中央电视台新闻联播的收视率,适宜用抽样调查方式;
D、了解某班学生“50m跑”的成绩,适宜用普查方式;
故选:D.
5.把一个长为5,宽为2的长方形的长减少x(0≤x<5),宽不变,所得长方形的面积y关于x的函数表达式为( )
A.y=﹣2x+10
B.y=5x
C.y=2x
D.y=10﹣x
【分析】长方形的长减少x(0≤x<5)得到长方形的长为5﹣x,宽不变,根据长方形的面积=长×宽即可得到y与x的函数表达式.
【解答】解:y=2(5﹣x)=﹣2x+10,
故选:A.
6.两根木条,一根长10cm,另一根长12cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A.1cm
B.11cm
C.1cm
或11cm
D.2cm或11cm
【分析】设较长的木条为AB,较短的木条为BC,根据中点定义求出BM、BN的长度,然后分两种情况:①BC不在AB上时,MN=BM+BN,②BC在AB上时,MN=BM﹣BN,分别代入数据进行计算即可得解.
【解答】解:如图,设较长的木条为AB=12cm,较短的木条为BC=10cm,
∵M、N分别为AB、BC的中点,
∴BM=6cm,BN=5cm,
①如图1,BC不在AB上时,MN=BM+BN=6+5=11cm,
②如图2,BC在AB上时,MN=BM﹣BN=6﹣5=1cm,
综上所述,两根木条的中点间的距离是1cm
或11cm,
故选:C.
7.如图所示,将四张全等的长方形硬纸片围成一个正方形,根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为( )
A.a2﹣b2=(a+b)(a﹣b)
B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=(a+b)2﹣4ab
D.a2+ab=a(a+b)
【分析】用两种方法正确的表示出阴影部分的面积,再根据图形阴影部分面积的关系,即可直观地得到一个关于a、b的恒等式.
【解答】解:方法一阴影部分的面积为:(a﹣b)2,
方法二阴影部分的面积为:(a+b)2﹣4ab,
所以根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为(a﹣b)2=(a+b)2﹣4ab.
故选:C.
8.如图,已知直线AB∥CD.DA⊥CE于点A.若∠D=36°20′,则∠EAB的度数是( )
A.63°40′
B.53°40′
C.44°40′
D.36°20′
【分析】先根据平行线的性质,即可得出∠BAD的度数,再根据垂直的定义,得出∠EAB的度数.
【解答】解:∵AB∥CD,∠D=36°20′,
∴∠BAD=∠D=36°20′,
∵DA⊥CE,
∴∠DAE=90°,
∴∠EAB=∠DAE﹣∠BAD=90°﹣36°20′=53°40′.
故选:B.
9.某学校为了加强学生的安全意识,组织学生观看了纪实片《孩子,请不要私自下水》,并对部分学生进行调查.根据下面两幅不完整的统计图可以求出,在这次调查中被调查的学生有( )
A.400名
B.380名
C.350名
D.300名
【分析】从两个统计图可得,“一定会”的有20人,占调查人数的5%,可求出调查人数.
【解答】解:20÷5%=400人,
故选:A.
10.为了建设社会主义新农村,我市积极推进“行政村通畅工程“,对甲村和乙村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,不过施工队随后加快了施工进度,按时完成了两村之间道路的改造,下面能反映该工程改造道路里程y(公里)与时间x(天)的函数关系大致的图象是( )
A.
B.
C.
D.
【分析】根据y随x的增大而减小,即可判断选项A错误;根据施工队在工作了一段时间后,因暴雨被迫停工几天,即可判断选项D错误;根据施工队随后加快了施工进度得出y随x的增大减小得比开始的快,即可判断选项A、C的正误.
【解答】解:∵y随x的增大而减小,
∴选项AD错误;
∵施工队在工作了一段时间后,因暴雨被迫停工几天,
∴选项C错误;
∵施工队随后加快了施工进度,
∴y随x的增大减小得比开始的快,
∴选项B正确;
故选:B.
11.有一个长方形内部剪掉了一个小长方形,它们的尺寸如图所示,则余下的部分(阴影部分)的面积( )
A.4a2
B.4a2﹣ab
C.4a2+ab
D.4a2﹣ab﹣2b2
【分析】根据阴影部分面积=大长方形的面积﹣小长方形的面积列出算式,再根据整式的混合运算顺序和运算法则计算可得.
【解答】解:余下的部分的面积为(2a+b)(2a﹣b)﹣b(a﹣b)
=4a2﹣b2﹣ab+b2
=4a2﹣ab,
故选:B.
12.在同一平面内,若∠A与∠B的两边分别平行,且∠A比∠B的3倍少40°,则∠A的度数为( )
A.20°
B.55°
C.20°或125°
D.20°或55°
【分析】根据平行线的性质即可求解.
【解答】解:∵两个角的两边分别平行,
∴这两个角大小相等或互补,
①这两个角大小相等,如下图所示:
由题意得,∠A=∠B,∠A=3∠B﹣40°,
∴∠A=∠B=20°,
②这两个角互补,如下图所示:
由题意得,∠A+∠B=180°,∠A=3∠B﹣40°,
∴∠B=55°,∠A=125°,
综上所述,∠A的度数为20°或125°,
故选:C.
二、填空题(共5小题,每小题4分,满分20分)
13.(4分)如图,点O在直线AE上,射线OC平分∠AOE.如果∠DOB=90°,∠1=25°,那么∠AOB的度数为 25° .
【分析】根据点O在直线AE上,OC平分∠AOE,可得∠AOC=90°,由∠DOB是直角,∠1=25°,可以求出∠BOC=65°,再根据∠AOB+∠BOC=∠AOC=90°求出∠AOB的度数.
【解答】解:∵点O在直线AE上,OC平分∠AOE,
∴∠AOC=∠COE=90°,
∵∠DOB是直角,∠1=25°,
∴∠BOC=∠DOB﹣∠1=90°﹣25°=65°,
∵∠AOB+∠BOC=∠AOC=90°,
∴∠AOB=90°﹣∠BOC=90°﹣65°=25°.
故答案为:25°.
14.(4分)已知10a=2,10b=3,则102a+3b= 108 .
【分析】根据幂的乘方进行计算即可.
【解答】解:∵10a=2,10b=3,
∴102a+3b=(10a)2?(10b)3=4×27=108,
故答案为108.
15.(4分)小鸡孵化场孵化出一批小鸡,工人在其中50只小鸡上做记号后让这批小鸡充分跑散,后来再任意抓出100只小鸡,其中有记号的有10只,则这批小鸡大约有 500 只.
【分析】用做标记的小鸡数量除以有记号小鸡的数量占被抽查小鸡数量的比例即可.
【解答】解:根据题意,这批小鸡的只数大约为50÷=500(只),
故答案为:500.
16.(4分)某市出租车白天的收费起步价为7元,即路程不超过3千米时收费7元,超过部分每千米收费1.2元,如果乘客白天乘坐出租车的路程为x(x>3)千米,乘车费为y元,那么y与x之间的关系为 y=1.2x+3.4 .
【分析】根据乘车费用=起步价+超过3千米的费用即可得出.
【解答】解:依据题意得:y=7+1.2(x﹣3)=1.2x+3.4,
故答案为:y=1.2x+3.4,
17.(4分)如图,已知AB∥CD,则∠A、∠C、∠P的关系为 ∠A+∠C﹣∠P=180° .
【分析】先作PE∥CD,根据两直线平行同旁内角互补可知∠C+∠CPE=180°,而AB∥CD,利用平行于同一直线的两条直线平行可得PE∥AB,再根据两直线平行内错角相等可知∠A=∠APE,于是有∠A=∠APC+∠CPE,即可求∠A+∠C﹣∠P=180°.
【解答】解:如右图所示,作PE∥CD,
∵PE∥CD,
∴∠C+∠CPE=180°,
又∵AB∥CD,
∴PE∥AB,
∴∠A=∠APE,
∴∠A+∠C﹣∠P=180°,
故答案为:∠A+∠C﹣∠P=180°.
三、解答题(共7小题,共70分)
18.(8分)化简:
(1)2(2x2﹣xy)+x(x﹣y);
(2)ab(2ab2﹣a2b)﹣(2ab)2b+a3b2.
【分析】(1)根据单项式乘多项式的运算法则计算;
(2)根据单项式乘多项式、积的乘方法则计算.
【解答】解:(1)2(2x2﹣xy)+x(x﹣y)
=4x2﹣2xy+x2﹣xy
=5x2﹣3xy;
(2)ab(2ab2﹣a2b)﹣(2ab)2b+a3b2
=2a2b3﹣a3b2﹣4a2b3+a3b2
=﹣2a2b3.
19.(8分)如图,点B是线段AC上一点,且AB=21cm,BC=AB.
(1)试求出线段AC的长;
(2)如果点O是线段AC的中点,请求线段OB的长.
【分析】(1)由B在线段AC上可知AC=AB+BC,把AB=21cm,BC=AB代入即可得到答案;
(2)根据O是线段AC的中点及AC的长可求出CO的长,由OB=CO﹣BC即可得出答案.
【解答】解:(1)∵AB=21cm,BC=AB=7cm,
∴AC=AB+BC=21+7=28(cm);
(2)由(1)知:AC=28cm,
∵点O是线段AC的中点,
∴CO=AC=×28=14(cm),
∴OB=CO﹣BC=14﹣7=7(cm).
20.(10分)某校进行“垃圾分一分,环境美十分”的主题宣传活动,随机调查了部分学生对垃圾分类知识的了解情况.调查选项分为“A:非常了解,B:比较了解,C:基本了解,D:不了解”四种,并将调查结果绘制成如图两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
(1)把两幅统计图补充完整;
(2)本次调查了 50 名学生;
(3)根据上述调查数据,请你提出一条合理化建议 “非常了解”的占比较小,需要进一步加强宣传的力度 .
【分析】(1)求出调查人数,各种情况的人数以及相应的占比,即可补全统计图;
(2)由(1)可得答案;
(3)根据“A非常了解”的占比,需要加强宣传,使了解程度增加.
【解答】解:(1)5÷10%=50(人),25÷50=50%,50×26%=13(人),50﹣5﹣25﹣13=7(人),7÷50=14%,
补全的统计图如图所示:
(2)5÷10%=50(人),
故答案为:50;
(3)根据对垃圾分类知识的了解情况,各占的百分比,对于“非常了解”的占比较小,需要进一步加强宣传的力度.
故答案为:“非常了解”的占比较小,需要进一步加强宣传的力度.
21.(10分)“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)小明在书店停留了多少分钟?
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
(4)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
【分析】(1)根据函数图象的纵坐标,可得答案;
(2)根据函数图象的横坐标,可得到达书店时间,离开书店时间,根据有理数的减法,可得答案;
(3)根据函数图象的纵坐标,可得相应的路程,根据有理数的加法,可得答案;
(4)根据函数图象的纵坐标,可得路程,根据函数图象的横坐标,可得时间,根据路程与时间的关系,可得速度.
【解答】解:(1)根据图象,学校的纵坐标为1500,小明家的纵坐标为0,
故小明家到学校的路程是1500米;
(2)根据题意,小明在书店停留的时间为从(8分)到(12分),
故小明在书店停留了4分钟.
(3)一共行驶的总路程=1200+(1200﹣600)+(1500﹣600)
=1200+600+900=2700米;
共用了14分钟.
(4)由图象可知:0~6分钟时,平均速度==200米/分,
6~8分钟时,平均速度==300米/分,
12~14分钟时,平均速度==450米/分,
所以,12~14分钟时速度最快,不在安全限度内.
22.(10分)如图,AC∥FE,∠1+∠3=180°.
(1)判定∠FAB与∠4的大小关系,并说明理由;
(2)若AC平分∠FAB,EF⊥BE于点E,∠4=78°,求∠BCD的度数.
【分析】(1)由已知可证得∠2=∠3,根据平行线的判定得到FA∥CD,根据平行线的性质即可得到∠FAB=∠4;
(2)根据角平分线的定义和平行线的判定和性质定理即可得到结论.
【解答】解:(1)∠FAB=∠4,
理由如下:
∵AC∥EF,
∴∠1+∠2=180°,
又∵∠1+∠3=180°,
∴∠2=∠3,
∴FA∥CD,
∴∠FAB=∠4;
(2)∵AC平分∠FAB,
∴∠2=∠CAD,
∵∠2=∠3,
∴∠CAD=∠3,
∵∠4=∠3+∠CAD,
∴,
∵EF⊥BE,AC∥EF,
∴AC⊥BE,
∴∠ACB=90°,
∴∠BCD=90°﹣∠3=51°.
23.(12分)如图1,将一个长为4a,宽为2b的长方形,沿图中虚线均匀分成4个小长方形,然后按图2形状拼成一个正方形.
(1)图2的空白部分的边长是多少?(用含a、b的式子表示)
(2)若2a+b=7,且ab=3,求图2中的空白正方形的面积.
(3)观察图2,用等式表示出(2a﹣b)2,ab和(2a+b)2的数量关系.
【分析】(1)观察由已知图形,得到四个小长方形的长为2a,宽为b,那么图2中的空白部分的正方形的边长是小长方形的长减去小长方形的宽.
(2)通过观察图形,大正方形的边长为小长方形的长和宽的和.图2中空白部分的正方形的面积为大正方形的面积减去四个小长方形的面积.
(3)通过观察图形知:(2a+b)2﹣(2a﹣b)2=8ab.分别表示的是大正方形、空白部分的正方形及4个小长方形的面积.
【解答】解:(1)图2的空白部分的边长是2a﹣b
(2)由图21﹣2可知,小正方形的面积=大正方形的面积﹣4个小长方形的面积,
∵大正方形的边长=2a+b=7,∴大正方形的面积=(2a+b)2=49,
又∵4个小长方形的面积之和=大长方形的面积=4a×2b=8ab=8×3=24,
∴小正方形的面积=(2a﹣b)2=49﹣24=25
(3)由图2可以看出,大正方形面积=空白部分的正方形的面积+四个小长方形的面积
即:(2a+b)2﹣(2a﹣b)2=8ab.
24.(12分)如图,AB∥CD,∠ABE=120°.
(1)如图①,写出∠BED与∠D的数量关系,并证明你的结论;
(2)如图②,∠DEF=2∠BEF,∠CDF=∠CDE,EF与DF交于点F,求∠EFD的度数;
(3)如图③,过B作BG⊥AB于G点,∠CDE=4∠GDE,求的值.
【分析】(1)如图①,延长AB交DE于点F,根据平行线的性质即可得结论∠BED+∠D=120°;
(2)设∠BEF=α,∠CDF=β,可得∠DEF=2α,∠DEB=3α,∠CDE=3β,∠EDF=2β,结合(1)可知∠BED+∠CDE=120°,进而可得结论;
(3)根据已知条件和三角形的外角可得∠G+30°=∠E+(120°﹣∠E),进而可得结论.
【解答】解:(1)结论:∠BED+∠D=120°,
证明:如图①,延长AB交DE于点F,
∵AB∥CD,
∴∠BFE=∠D,
∵∠ABE=120°,
∴∠BFE+∠BED=∠ABE=120°,
∴∠D+∠BED=120°;
(2)如图②,
∵∠DEF=2∠BEF,∠CDF=∠CDE,
即∠CDE=3∠CDF,
设∠BEF=α,∠CDF=β,
∴∠DEF=2α,∠DEB=3α,∠CDE=3β,∠EDF=2β,
由(1)知:∠BED+∠CDE=120°,
∴3α+3β=120°,
∴α+β=40°,
∴2α+2β=80°,
∴∠EFD=180°﹣∠DEF﹣∠EDF=180°﹣(2α+2β)=180°﹣80°=100°,
答:∠EFD的度数为100°;
(3)如图③,
∵BG⊥AB,
∴∠ABG=90°,
∵∠ABE=120°.
∴∠GBE=∠ABE﹣∠ABG=30°,
∵∠CDE=4∠GDE,
∴∠GDE=∠CDE,
∵∠G+∠GBE=∠E+∠GDE,
∴∠G+30°=∠E+∠CDE,
由(1)知:∠BED+∠CDE=120°,
∴∠CDE=120°﹣∠E,
∴∠G+30°=∠E+(120°﹣∠E),
∴∠G=∠E,
∴=.
一、选择题(本题有12小题,每小题5分,共60分,每小题只有一个选项是正确的,不选、多选、错选,均不得分)
1.如图,能用∠AOB,∠O,∠1三种方法表示同一个角的图形是( )
A.
B.
C.
D.
2.下列计算正确的是( )
A.a3﹣a2=a
B.a6÷a2=a3
C.a6﹣a2=a4
D.a3÷a2=a
3.根据语句“直线l1与直线l2相交,点M在直线l1上,直线l2不经过点M.”画出的图形是( )
A.
B.
C.
D.
4.下列调查中,适宜用普查方式的是( )
A.了解一批袋装食品是否含有防腐剂
B.了解一批灯泡的使用寿命
C.了解中央电视台新闻联播的收视率
D.了解某班学生“50m跑”的成绩
5.把一个长为5,宽为2的长方形的长减少x(0≤x<5),宽不变,所得长方形的面积y关于x的函数表达式为( )
A.y=﹣2x+10
B.y=5x
C.y=2x
D.y=10﹣x
6.两根木条,一根长10cm,另一根长12cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A.1cm
B.11cm
C.1cm
或11cm
D.2cm或11cm
7.如图所示,将四张全等的长方形硬纸片围成一个正方形,根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为( )
A.a2﹣b2=(a+b)(a﹣b)
B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=(a+b)2﹣4ab
D.a2+ab=a(a+b)
8.如图,已知直线AB∥CD.DA⊥CE于点A.若∠D=36°20′,则∠EAB的度数是( )
A.63°40′
B.53°40′
C.44°40′
D.36°20′
9.某学校为了加强学生的安全意识,组织学生观看了纪实片《孩子,请不要私自下水》,并对部分学生进行调查.根据下面两幅不完整的统计图可以求出,在这次调查中被调查的学生有( )
A.400名
B.380名
C.350名
D.300名
10.为了建设社会主义新农村,我市积极推进“行政村通畅工程“,对甲村和乙村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,不过施工队随后加快了施工进度,按时完成了两村之间道路的改造,下面能反映该工程改造道路里程y(公里)与时间x(天)的函数关系大致的图象是( )
A.
B.
C.
D.
11.有一个长方形内部剪掉了一个小长方形,它们的尺寸如图所示,则余下的部分(阴影部分)的面积( )
A.4a2
B.4a2﹣ab
C.4a2+ab
D.4a2﹣ab﹣2b2
12.在同一平面内,若∠A与∠B的两边分别平行,且∠A比∠B的3倍少40°,则∠A的度数为( )
A.20°
B.55°
C.20°或125°
D.20°或55°
二、填空题(共5小题,每小题4分,满分20分)
13.(4分)如图,点O在直线AE上,射线OC平分∠AOE.如果∠DOB=90°,∠1=25°,那么∠AOB的度数为
.
14.(4分)已知10a=2,10b=3,则102a+3b=
.
15.(4分)小鸡孵化场孵化出一批小鸡,工人在其中50只小鸡上做记号后让这批小鸡充分跑散,后来再任意抓出100只小鸡,其中有记号的有10只,则这批小鸡大约有
只.
16.(4分)某市出租车白天的收费起步价为7元,即路程不超过3千米时收费7元,超过部分每千米收费1.2元,如果乘客白天乘坐出租车的路程为x(x>3)千米,乘车费为y元,那么y与x之间的关系为
.
17.(4分)如图,已知AB∥CD,则∠A、∠C、∠P的关系为
.
三、解答题(共7小题,共70分)
18.(8分)化简:
(1)2(2x2﹣xy)+x(x﹣y);
(2)ab(2ab2﹣a2b)﹣(2ab)2b+a3b2.
19.(8分)如图,点B是线段AC上一点,且AB=21cm,BC=AB.
(1)试求出线段AC的长;
(2)如果点O是线段AC的中点,请求线段OB的长.
20.(10分)某校进行“垃圾分一分,环境美十分”的主题宣传活动,随机调查了部分学生对垃圾分类知识的了解情况.调查选项分为“A:非常了解,B:比较了解,C:基本了解,D:不了解”四种,并将调查结果绘制成如图两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
(1)把两幅统计图补充完整;
(2)本次调查了
名学生;
(3)根据上述调查数据,请你提出一条合理化建议
.
21.(10分)“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)小明在书店停留了多少分钟?
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
(4)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
22.(10分)如图,AC∥FE,∠1+∠3=180°.
(1)判定∠FAB与∠4的大小关系,并说明理由;
(2)若AC平分∠FAB,EF⊥BE于点E,∠4=78°,求∠BCD的度数.
23.(12分)如图1,将一个长为4a,宽为2b的长方形,沿图中虚线均匀分成4个小长方形,然后按图2形状拼成一个正方形.
(1)图2的空白部分的边长是多少?(用含a、b的式子表示)
(2)若2a+b=7,且ab=3,求图2中的空白正方形的面积.
(3)观察图2,用等式表示出(2a﹣b)2,ab和(2a+b)2的数量关系.
24.(12分)如图,AB∥CD,∠ABE=120°.
(1)如图①,写出∠BED与∠D的数量关系,并证明你的结论;
(2)如图②,∠DEF=2∠BEF,∠CDF=∠CDE,EF与DF交于点F,求∠EFD的度数;
(3)如图③,过B作BG⊥AB于G点,∠CDE=4∠GDE,求的值.
2020-2021学年山东省淄博市高青县六年级(下)期末数学试卷(五四学制)
参考答案与试题解析
一、选择题(本题有12小题,每小题5分,共60分,每小题只有一个选项是正确的,不选、多选、错选,均不得分)
1.如图,能用∠AOB,∠O,∠1三种方法表示同一个角的图形是( )
A.
B.
C.
D.
【分析】直接利用角的概念分析得出答案.
【解答】解:A、∠O无法表示一个角,故此选项不合题意;
B、∠AOB,∠O,∠1三种方法表示同一个角的图形,符合题意;
C、∠O无法表示一个角,故此选项不合题意;
D、∠O无法表示一个角,故此选项不合题意;
故选:B.
2.下列计算正确的是( )
A.a3﹣a2=a
B.a6÷a2=a3
C.a6﹣a2=a4
D.a3÷a2=a
【分析】直接利用合并同类项法则以及同底数幂的除法运算法则分别计算得出答案.
【解答】解:A、a3﹣a2无法计算,故此选项错误;
B、a6÷a2=a4,故此选项错误;
C、a6﹣a2无法计算,故此选项错误;
D、a3÷a2=a,故此选项正确.
故选:D.
3.根据语句“直线l1与直线l2相交,点M在直线l1上,直线l2不经过点M.”画出的图形是( )
A.
B.
C.
D.
【分析】根据直线l1与直线l2相交,点M在直线l1上,直线l2不经过点M进行判断,即可得出结论.
【解答】解:A.直线l2不经过点M,故本选项不合题意;
B.点M在直线l1上,故本选项不合题意;
C.点M在直线l1上,故本选项不合题意;
D.直线l1与直线l2相交,点M在直线l1上,直线l2不经过点M,故本选项符合题意;
故选:D.
4.下列调查中,适宜用普查方式的是( )
A.了解一批袋装食品是否含有防腐剂
B.了解一批灯泡的使用寿命
C.了解中央电视台新闻联播的收视率
D.了解某班学生“50m跑”的成绩
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
【解答】解:A、了解一批袋装食品是否含有防腐剂,适宜用抽样调查方式;
B、了解一批灯泡的使用寿命,适宜用抽样调查方式;
C、了解中央电视台新闻联播的收视率,适宜用抽样调查方式;
D、了解某班学生“50m跑”的成绩,适宜用普查方式;
故选:D.
5.把一个长为5,宽为2的长方形的长减少x(0≤x<5),宽不变,所得长方形的面积y关于x的函数表达式为( )
A.y=﹣2x+10
B.y=5x
C.y=2x
D.y=10﹣x
【分析】长方形的长减少x(0≤x<5)得到长方形的长为5﹣x,宽不变,根据长方形的面积=长×宽即可得到y与x的函数表达式.
【解答】解:y=2(5﹣x)=﹣2x+10,
故选:A.
6.两根木条,一根长10cm,另一根长12cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A.1cm
B.11cm
C.1cm
或11cm
D.2cm或11cm
【分析】设较长的木条为AB,较短的木条为BC,根据中点定义求出BM、BN的长度,然后分两种情况:①BC不在AB上时,MN=BM+BN,②BC在AB上时,MN=BM﹣BN,分别代入数据进行计算即可得解.
【解答】解:如图,设较长的木条为AB=12cm,较短的木条为BC=10cm,
∵M、N分别为AB、BC的中点,
∴BM=6cm,BN=5cm,
①如图1,BC不在AB上时,MN=BM+BN=6+5=11cm,
②如图2,BC在AB上时,MN=BM﹣BN=6﹣5=1cm,
综上所述,两根木条的中点间的距离是1cm
或11cm,
故选:C.
7.如图所示,将四张全等的长方形硬纸片围成一个正方形,根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为( )
A.a2﹣b2=(a+b)(a﹣b)
B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=(a+b)2﹣4ab
D.a2+ab=a(a+b)
【分析】用两种方法正确的表示出阴影部分的面积,再根据图形阴影部分面积的关系,即可直观地得到一个关于a、b的恒等式.
【解答】解:方法一阴影部分的面积为:(a﹣b)2,
方法二阴影部分的面积为:(a+b)2﹣4ab,
所以根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为(a﹣b)2=(a+b)2﹣4ab.
故选:C.
8.如图,已知直线AB∥CD.DA⊥CE于点A.若∠D=36°20′,则∠EAB的度数是( )
A.63°40′
B.53°40′
C.44°40′
D.36°20′
【分析】先根据平行线的性质,即可得出∠BAD的度数,再根据垂直的定义,得出∠EAB的度数.
【解答】解:∵AB∥CD,∠D=36°20′,
∴∠BAD=∠D=36°20′,
∵DA⊥CE,
∴∠DAE=90°,
∴∠EAB=∠DAE﹣∠BAD=90°﹣36°20′=53°40′.
故选:B.
9.某学校为了加强学生的安全意识,组织学生观看了纪实片《孩子,请不要私自下水》,并对部分学生进行调查.根据下面两幅不完整的统计图可以求出,在这次调查中被调查的学生有( )
A.400名
B.380名
C.350名
D.300名
【分析】从两个统计图可得,“一定会”的有20人,占调查人数的5%,可求出调查人数.
【解答】解:20÷5%=400人,
故选:A.
10.为了建设社会主义新农村,我市积极推进“行政村通畅工程“,对甲村和乙村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,不过施工队随后加快了施工进度,按时完成了两村之间道路的改造,下面能反映该工程改造道路里程y(公里)与时间x(天)的函数关系大致的图象是( )
A.
B.
C.
D.
【分析】根据y随x的增大而减小,即可判断选项A错误;根据施工队在工作了一段时间后,因暴雨被迫停工几天,即可判断选项D错误;根据施工队随后加快了施工进度得出y随x的增大减小得比开始的快,即可判断选项A、C的正误.
【解答】解:∵y随x的增大而减小,
∴选项AD错误;
∵施工队在工作了一段时间后,因暴雨被迫停工几天,
∴选项C错误;
∵施工队随后加快了施工进度,
∴y随x的增大减小得比开始的快,
∴选项B正确;
故选:B.
11.有一个长方形内部剪掉了一个小长方形,它们的尺寸如图所示,则余下的部分(阴影部分)的面积( )
A.4a2
B.4a2﹣ab
C.4a2+ab
D.4a2﹣ab﹣2b2
【分析】根据阴影部分面积=大长方形的面积﹣小长方形的面积列出算式,再根据整式的混合运算顺序和运算法则计算可得.
【解答】解:余下的部分的面积为(2a+b)(2a﹣b)﹣b(a﹣b)
=4a2﹣b2﹣ab+b2
=4a2﹣ab,
故选:B.
12.在同一平面内,若∠A与∠B的两边分别平行,且∠A比∠B的3倍少40°,则∠A的度数为( )
A.20°
B.55°
C.20°或125°
D.20°或55°
【分析】根据平行线的性质即可求解.
【解答】解:∵两个角的两边分别平行,
∴这两个角大小相等或互补,
①这两个角大小相等,如下图所示:
由题意得,∠A=∠B,∠A=3∠B﹣40°,
∴∠A=∠B=20°,
②这两个角互补,如下图所示:
由题意得,∠A+∠B=180°,∠A=3∠B﹣40°,
∴∠B=55°,∠A=125°,
综上所述,∠A的度数为20°或125°,
故选:C.
二、填空题(共5小题,每小题4分,满分20分)
13.(4分)如图,点O在直线AE上,射线OC平分∠AOE.如果∠DOB=90°,∠1=25°,那么∠AOB的度数为 25° .
【分析】根据点O在直线AE上,OC平分∠AOE,可得∠AOC=90°,由∠DOB是直角,∠1=25°,可以求出∠BOC=65°,再根据∠AOB+∠BOC=∠AOC=90°求出∠AOB的度数.
【解答】解:∵点O在直线AE上,OC平分∠AOE,
∴∠AOC=∠COE=90°,
∵∠DOB是直角,∠1=25°,
∴∠BOC=∠DOB﹣∠1=90°﹣25°=65°,
∵∠AOB+∠BOC=∠AOC=90°,
∴∠AOB=90°﹣∠BOC=90°﹣65°=25°.
故答案为:25°.
14.(4分)已知10a=2,10b=3,则102a+3b= 108 .
【分析】根据幂的乘方进行计算即可.
【解答】解:∵10a=2,10b=3,
∴102a+3b=(10a)2?(10b)3=4×27=108,
故答案为108.
15.(4分)小鸡孵化场孵化出一批小鸡,工人在其中50只小鸡上做记号后让这批小鸡充分跑散,后来再任意抓出100只小鸡,其中有记号的有10只,则这批小鸡大约有 500 只.
【分析】用做标记的小鸡数量除以有记号小鸡的数量占被抽查小鸡数量的比例即可.
【解答】解:根据题意,这批小鸡的只数大约为50÷=500(只),
故答案为:500.
16.(4分)某市出租车白天的收费起步价为7元,即路程不超过3千米时收费7元,超过部分每千米收费1.2元,如果乘客白天乘坐出租车的路程为x(x>3)千米,乘车费为y元,那么y与x之间的关系为 y=1.2x+3.4 .
【分析】根据乘车费用=起步价+超过3千米的费用即可得出.
【解答】解:依据题意得:y=7+1.2(x﹣3)=1.2x+3.4,
故答案为:y=1.2x+3.4,
17.(4分)如图,已知AB∥CD,则∠A、∠C、∠P的关系为 ∠A+∠C﹣∠P=180° .
【分析】先作PE∥CD,根据两直线平行同旁内角互补可知∠C+∠CPE=180°,而AB∥CD,利用平行于同一直线的两条直线平行可得PE∥AB,再根据两直线平行内错角相等可知∠A=∠APE,于是有∠A=∠APC+∠CPE,即可求∠A+∠C﹣∠P=180°.
【解答】解:如右图所示,作PE∥CD,
∵PE∥CD,
∴∠C+∠CPE=180°,
又∵AB∥CD,
∴PE∥AB,
∴∠A=∠APE,
∴∠A+∠C﹣∠P=180°,
故答案为:∠A+∠C﹣∠P=180°.
三、解答题(共7小题,共70分)
18.(8分)化简:
(1)2(2x2﹣xy)+x(x﹣y);
(2)ab(2ab2﹣a2b)﹣(2ab)2b+a3b2.
【分析】(1)根据单项式乘多项式的运算法则计算;
(2)根据单项式乘多项式、积的乘方法则计算.
【解答】解:(1)2(2x2﹣xy)+x(x﹣y)
=4x2﹣2xy+x2﹣xy
=5x2﹣3xy;
(2)ab(2ab2﹣a2b)﹣(2ab)2b+a3b2
=2a2b3﹣a3b2﹣4a2b3+a3b2
=﹣2a2b3.
19.(8分)如图,点B是线段AC上一点,且AB=21cm,BC=AB.
(1)试求出线段AC的长;
(2)如果点O是线段AC的中点,请求线段OB的长.
【分析】(1)由B在线段AC上可知AC=AB+BC,把AB=21cm,BC=AB代入即可得到答案;
(2)根据O是线段AC的中点及AC的长可求出CO的长,由OB=CO﹣BC即可得出答案.
【解答】解:(1)∵AB=21cm,BC=AB=7cm,
∴AC=AB+BC=21+7=28(cm);
(2)由(1)知:AC=28cm,
∵点O是线段AC的中点,
∴CO=AC=×28=14(cm),
∴OB=CO﹣BC=14﹣7=7(cm).
20.(10分)某校进行“垃圾分一分,环境美十分”的主题宣传活动,随机调查了部分学生对垃圾分类知识的了解情况.调查选项分为“A:非常了解,B:比较了解,C:基本了解,D:不了解”四种,并将调查结果绘制成如图两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
(1)把两幅统计图补充完整;
(2)本次调查了 50 名学生;
(3)根据上述调查数据,请你提出一条合理化建议 “非常了解”的占比较小,需要进一步加强宣传的力度 .
【分析】(1)求出调查人数,各种情况的人数以及相应的占比,即可补全统计图;
(2)由(1)可得答案;
(3)根据“A非常了解”的占比,需要加强宣传,使了解程度增加.
【解答】解:(1)5÷10%=50(人),25÷50=50%,50×26%=13(人),50﹣5﹣25﹣13=7(人),7÷50=14%,
补全的统计图如图所示:
(2)5÷10%=50(人),
故答案为:50;
(3)根据对垃圾分类知识的了解情况,各占的百分比,对于“非常了解”的占比较小,需要进一步加强宣传的力度.
故答案为:“非常了解”的占比较小,需要进一步加强宣传的力度.
21.(10分)“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)小明在书店停留了多少分钟?
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
(4)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
【分析】(1)根据函数图象的纵坐标,可得答案;
(2)根据函数图象的横坐标,可得到达书店时间,离开书店时间,根据有理数的减法,可得答案;
(3)根据函数图象的纵坐标,可得相应的路程,根据有理数的加法,可得答案;
(4)根据函数图象的纵坐标,可得路程,根据函数图象的横坐标,可得时间,根据路程与时间的关系,可得速度.
【解答】解:(1)根据图象,学校的纵坐标为1500,小明家的纵坐标为0,
故小明家到学校的路程是1500米;
(2)根据题意,小明在书店停留的时间为从(8分)到(12分),
故小明在书店停留了4分钟.
(3)一共行驶的总路程=1200+(1200﹣600)+(1500﹣600)
=1200+600+900=2700米;
共用了14分钟.
(4)由图象可知:0~6分钟时,平均速度==200米/分,
6~8分钟时,平均速度==300米/分,
12~14分钟时,平均速度==450米/分,
所以,12~14分钟时速度最快,不在安全限度内.
22.(10分)如图,AC∥FE,∠1+∠3=180°.
(1)判定∠FAB与∠4的大小关系,并说明理由;
(2)若AC平分∠FAB,EF⊥BE于点E,∠4=78°,求∠BCD的度数.
【分析】(1)由已知可证得∠2=∠3,根据平行线的判定得到FA∥CD,根据平行线的性质即可得到∠FAB=∠4;
(2)根据角平分线的定义和平行线的判定和性质定理即可得到结论.
【解答】解:(1)∠FAB=∠4,
理由如下:
∵AC∥EF,
∴∠1+∠2=180°,
又∵∠1+∠3=180°,
∴∠2=∠3,
∴FA∥CD,
∴∠FAB=∠4;
(2)∵AC平分∠FAB,
∴∠2=∠CAD,
∵∠2=∠3,
∴∠CAD=∠3,
∵∠4=∠3+∠CAD,
∴,
∵EF⊥BE,AC∥EF,
∴AC⊥BE,
∴∠ACB=90°,
∴∠BCD=90°﹣∠3=51°.
23.(12分)如图1,将一个长为4a,宽为2b的长方形,沿图中虚线均匀分成4个小长方形,然后按图2形状拼成一个正方形.
(1)图2的空白部分的边长是多少?(用含a、b的式子表示)
(2)若2a+b=7,且ab=3,求图2中的空白正方形的面积.
(3)观察图2,用等式表示出(2a﹣b)2,ab和(2a+b)2的数量关系.
【分析】(1)观察由已知图形,得到四个小长方形的长为2a,宽为b,那么图2中的空白部分的正方形的边长是小长方形的长减去小长方形的宽.
(2)通过观察图形,大正方形的边长为小长方形的长和宽的和.图2中空白部分的正方形的面积为大正方形的面积减去四个小长方形的面积.
(3)通过观察图形知:(2a+b)2﹣(2a﹣b)2=8ab.分别表示的是大正方形、空白部分的正方形及4个小长方形的面积.
【解答】解:(1)图2的空白部分的边长是2a﹣b
(2)由图21﹣2可知,小正方形的面积=大正方形的面积﹣4个小长方形的面积,
∵大正方形的边长=2a+b=7,∴大正方形的面积=(2a+b)2=49,
又∵4个小长方形的面积之和=大长方形的面积=4a×2b=8ab=8×3=24,
∴小正方形的面积=(2a﹣b)2=49﹣24=25
(3)由图2可以看出,大正方形面积=空白部分的正方形的面积+四个小长方形的面积
即:(2a+b)2﹣(2a﹣b)2=8ab.
24.(12分)如图,AB∥CD,∠ABE=120°.
(1)如图①,写出∠BED与∠D的数量关系,并证明你的结论;
(2)如图②,∠DEF=2∠BEF,∠CDF=∠CDE,EF与DF交于点F,求∠EFD的度数;
(3)如图③,过B作BG⊥AB于G点,∠CDE=4∠GDE,求的值.
【分析】(1)如图①,延长AB交DE于点F,根据平行线的性质即可得结论∠BED+∠D=120°;
(2)设∠BEF=α,∠CDF=β,可得∠DEF=2α,∠DEB=3α,∠CDE=3β,∠EDF=2β,结合(1)可知∠BED+∠CDE=120°,进而可得结论;
(3)根据已知条件和三角形的外角可得∠G+30°=∠E+(120°﹣∠E),进而可得结论.
【解答】解:(1)结论:∠BED+∠D=120°,
证明:如图①,延长AB交DE于点F,
∵AB∥CD,
∴∠BFE=∠D,
∵∠ABE=120°,
∴∠BFE+∠BED=∠ABE=120°,
∴∠D+∠BED=120°;
(2)如图②,
∵∠DEF=2∠BEF,∠CDF=∠CDE,
即∠CDE=3∠CDF,
设∠BEF=α,∠CDF=β,
∴∠DEF=2α,∠DEB=3α,∠CDE=3β,∠EDF=2β,
由(1)知:∠BED+∠CDE=120°,
∴3α+3β=120°,
∴α+β=40°,
∴2α+2β=80°,
∴∠EFD=180°﹣∠DEF﹣∠EDF=180°﹣(2α+2β)=180°﹣80°=100°,
答:∠EFD的度数为100°;
(3)如图③,
∵BG⊥AB,
∴∠ABG=90°,
∵∠ABE=120°.
∴∠GBE=∠ABE﹣∠ABG=30°,
∵∠CDE=4∠GDE,
∴∠GDE=∠CDE,
∵∠G+∠GBE=∠E+∠GDE,
∴∠G+30°=∠E+∠CDE,
由(1)知:∠BED+∠CDE=120°,
∴∠CDE=120°﹣∠E,
∴∠G+30°=∠E+(120°﹣∠E),
∴∠G=∠E,
∴=.
同课章节目录
