人教版8年级数学(上册)同步课时导学案:11.2.1 第2课时 直角三角形的性质和判定(含答案)
文档属性
| 名称 | 人教版8年级数学(上册)同步课时导学案:11.2.1 第2课时 直角三角形的性质和判定(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 21:30:50 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十一章
三角形
(
教学备注
学生在课前完成自主学习部分
)11.2
与三角形有关的角
11.2.1
三角形的内角
第2课时
直角三角形的性质和判定
学习目标:1.了解直角三角形两个锐角的关系.
2.掌握直角三角形的判定.
3.会运用直角三角形的性质和判定进行相关计算.
重点:掌握直角三角形的性质和判定.
难点:运用直角三角形的性质和判定进行相关计算.
(
自主学习
)
一、知识链接
1.三角形的内角和为_______.
2.直角三角形有什么特点?
二、新知预习
1.如图,在△ABC中,已知∠C=90°.
△ABC叫做___________,用符号表示为__________;
∠A+∠B+∠C=_____°,∠A+∠B=_____°-∠C=_______°.
结论:直角三角形的两个锐角___________.
图
图
2.如图,在△ABC中,已知∠A+∠B=90°,
则∠C=_______°-(∠A+∠B)=_______°.
所以△ABC是_________.
结论:有两个角_______的三角形是直角三角形.
三、自学自测
1.在Rt△ABC中,∠B=90°,∠C=50°,则∠A=_______.
2.在△ABC中,若∠A=35°,∠C=55°,则△ABC是_________三角形.
四、我的疑惑
____________________________________________________________________________________________________________________________
(
教学备注
配套
PPT
讲授
1.情景引入
(见
幻灯片3-4
)
2.探究点1新知讲授
(见
幻灯片5-12
)
)
(
课堂探究
)
要点探究
探究点1:直角三角形的两个锐角互余
问题引导
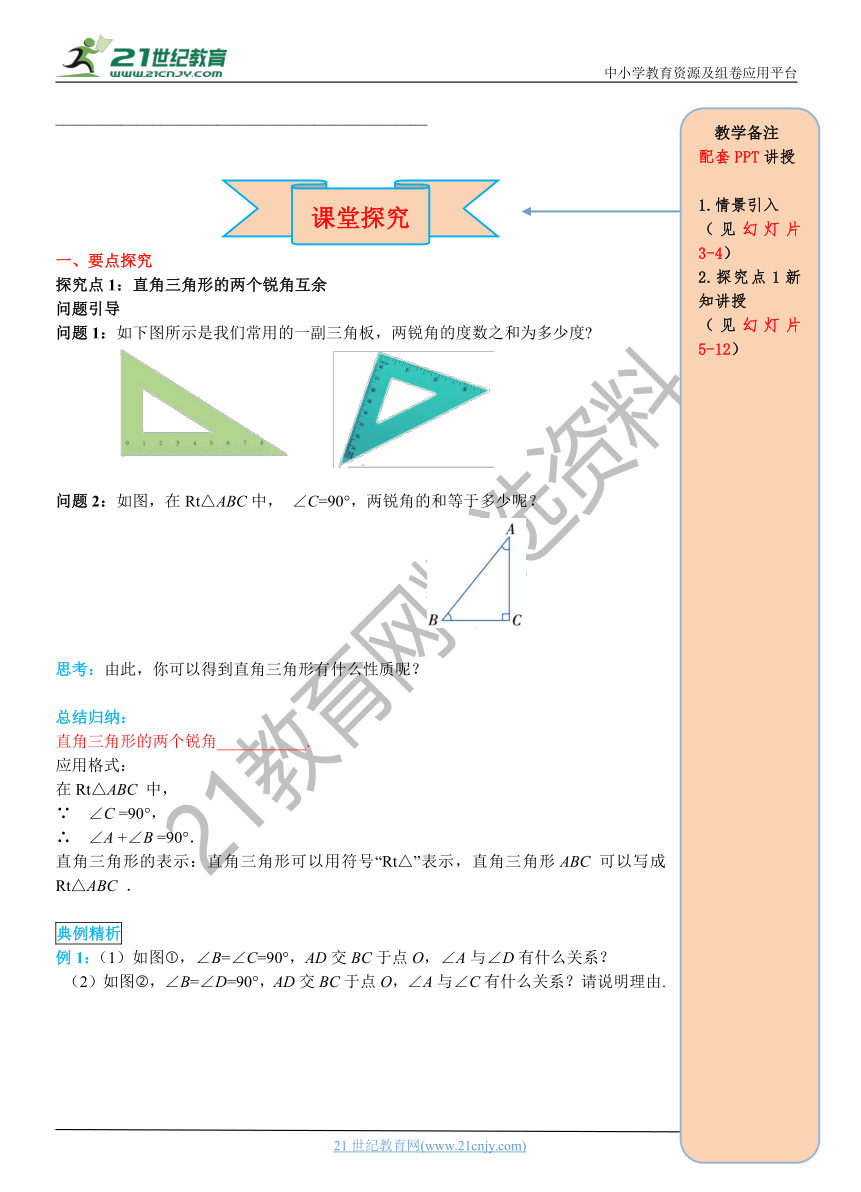
问题1:如下图所示是我们常用的一副三角板,两锐角的度数之和为多少度?
问题2:如图,在Rt△ABC中,
∠C=90°,两锐角的和等于多少呢?
思考:由此,你可以得到直角三角形有什么性质呢?
总结归纳:
直角三角形的两个锐角___________.
应用格式:
在Rt△ABC
中,
∵ ∠C
=90°,
∴ ∠A
+∠B
=90°.
直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角三角形ABC
可以写成Rt△ABC
.
典例精析
例1:(1)如图,∠B=∠C=90°,AD交BC于点O,∠A与∠D有什么关系?
(2)如图,∠B=∠D=90°,AD交BC于点O,∠A与∠C有什么关系?请说明理由.
(
教学备注
3.探究点2新知讲授
(见
幻灯片13-16
)
)
图
图
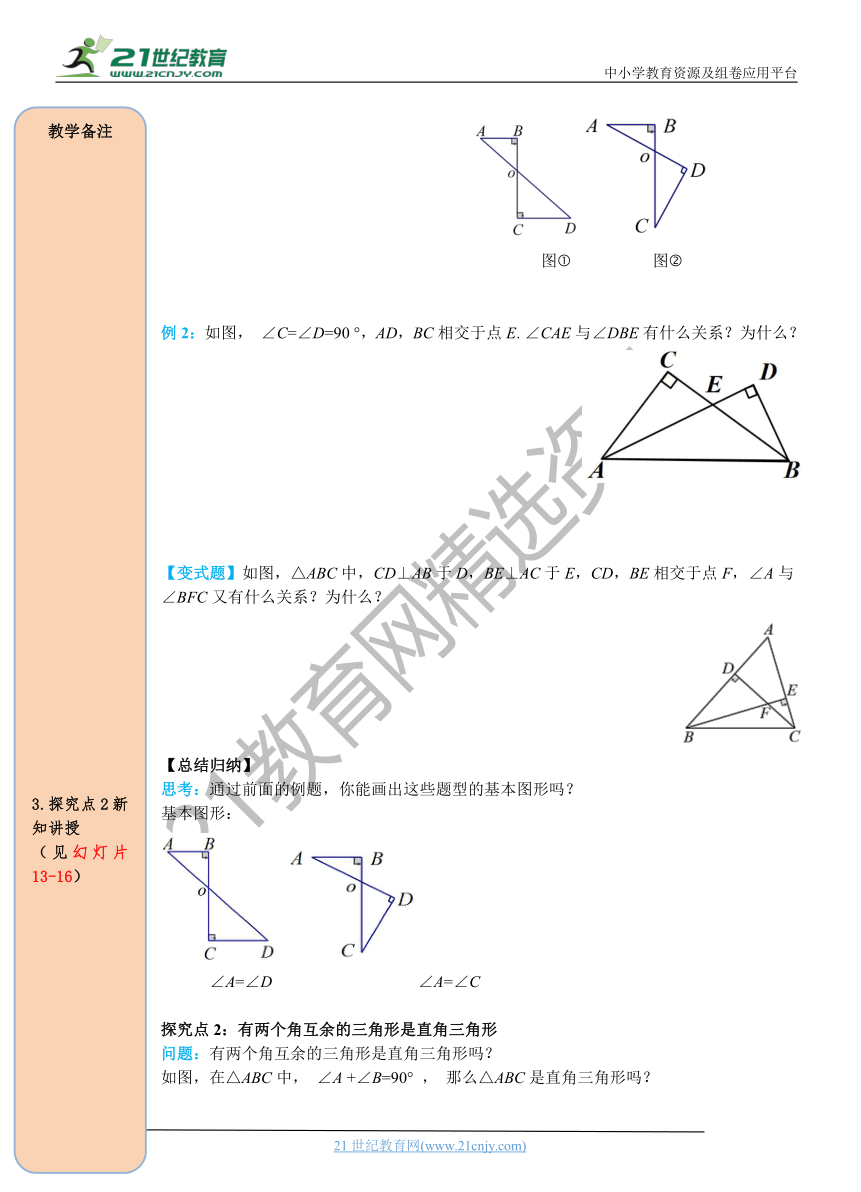
例2:如图,
∠C=∠D=90
°,AD,BC相交于点E.
∠CAE与∠DBE有什么关系?为什么?
【变式题】如图,△ABC中,CD⊥AB于D,BE⊥AC于E,CD,BE相交于点F,∠A与∠BFC又有什么关系?为什么?
【总结归纳】
思考:通过前面的例题,你能画出这些题型的基本图形吗?
基本图形:
∠A=∠D
∠A=∠C
探究点2:有两个角互余的三角形是直角三角形
问题:有两个角互余的三角形是直角三角形吗?
如图,在△ABC中,
∠A
+∠B=90°
,
那么△ABC是直角三角形吗?
总结归纳:有两个角互余的三角形是直角三角形.
应用格式:
在△ABC
中,
∵∠A
+∠B
=90°,
∴△ABC
是直角三角形.
(
教学备注
配套
PPT
讲授
4.课堂小结(见
幻灯片21
)
5.当堂检测
(见
幻灯片17-20
)
)典例精析
例3:如图,∠C=90
°,
∠1=
∠2,△ADE是直角三角形吗?为什么?
例4:如图,CE⊥AD,垂足为E,∠A=∠C,△ABD是直角三角形吗?为什么?
二、课堂小结
直角三角形(表示:Rt△)
性质:直角三角形两锐角互余.
如图,若△ABC为直角三角形,且∠A为直角,则∠B+∠C=90°.
(
B
)
(
C
)
(
A
)
判定:有两个角互余的三角形为直角三角形.
如图,若∠B+∠C=90°,则△ABC为直角三角形.
(
教学备注
)
(
当堂检测
)
1.如图,一张长方形纸片,剪去一部分后得到一个三角形,则图中∠1+∠2的度数是________.
2.如图,AB、CD相交于点O,AC⊥CD于点C,若∠BOD=38°,则∠A=________.
3.在△ABC中,若∠A=43°,∠B=47°,则这个三角形是____________.
4.在一个直角三角形中,有一个锐角等于40°,则另一个锐角的度数是( )
A.40°
B.50°
C.60°
D.70°
5.具备下列条件的△ABC中,不是直角三角形的是
(
)
A.∠A+∠B=∠C
B.∠A-∠B=∠C
C.∠A:∠B:∠C=1:2:3
D.∠A=∠B=3∠C
6.如图所示,△ABC为直角三角形,∠ACB=90°,CD⊥AB,与∠1互余的角有( )
A.∠B
B.∠A
C.∠BCD和∠A
D.∠BCD
如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.
求证:△ACD是直角三角形.
参考答案
自主学习
一、知识链接
1.180°
2.直角三角形有一个内角是90°.
二、新知预习
1.(1)直角三角形
Rt△ABC
(2)180
90
90
互余
2.180
90
直角三角形
互余
三、自学自测
1.40°
2.直角
四、我的疑惑
课堂探究
要点探究
探究点1:直角三角形的两个锐角互余
问题引导
问题1
30°+60°=90°
45°+45°=90°
问题2
解:在Rt△ABC中,因为
∠C=90°,由三角形内角和定理,得∠A
+∠B+∠C=90°,即∠A
+∠B=90°.
总结归纳
互余
典例精析
例1
解:(1)方法一(利用平行的判定和性质):
∵∠B=∠C=90°,∴AB∥CD,∴∠A=∠D.
方法二(利用直角三角形的性质):
∵∠B=∠C=90°,∴∠A+∠AOB=90°,∠D+∠COD=90°.
∵∠AOB=∠COD,∴∠A=∠D.
(2)解:∠A=∠C.理由如下:
∵∠B=∠D=90°,∴∠A+∠AOB=90°,∠C+∠COD=90°.
∵∠AOB=∠COD,∴∠A=∠C.
例2
解:在Rt△ACE中,∠CAE=90
°-
∠AEC.
在Rt△BDE中,∠DBE=90
°-
∠BED.
∵∠AEC=
∠BED,∴∠CAE=
∠DBE.
【变式题】
解:∵CD⊥AB于点D,BE⊥AC于点E,
∴∠BEA=∠BDF=90°,∴∠ABE+∠A=90°,∠ABE+∠DFB=90°.
∴∠A=∠DFB.∵∠DFB+∠BFC=180°,∴∠A+∠BFC=180°.
探究点2:有两个角互余的三角形是直角三角形
问题
解:在△ABC中,因为
∠A
+∠B
+∠C=180°,
又∠A
+∠B=90°,所以∠C=90°.
于是△ABC是直角三角形.
典例精析
例3
解:在Rt△ABC中,∠2+
∠A=90
°.
∵
∠1=
∠2,
∴∠1
+
∠A=90
°.即△ADE是直角三角形.
例4
解:△ABD是直角三角形.理由如下:
∵CE⊥AD,∴∠CED=90°,∴∠C+∠D=90°.
∵∠A=∠C,∴∠A+∠D=90°,∴△ABD是直角三角形.
当堂检测
1.90°
2.52°
3.直角三角形
4.B
5.D
6.C
证明:∵∠ACB=90°,∴∠A+∠B=90°.
∵∠ACD=∠B,∴∠A+∠ACD=90°,∴△ACD是直角三角形.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
第十一章
三角形
(
教学备注
学生在课前完成自主学习部分
)11.2
与三角形有关的角
11.2.1
三角形的内角
第2课时
直角三角形的性质和判定
学习目标:1.了解直角三角形两个锐角的关系.
2.掌握直角三角形的判定.
3.会运用直角三角形的性质和判定进行相关计算.
重点:掌握直角三角形的性质和判定.
难点:运用直角三角形的性质和判定进行相关计算.
(
自主学习
)
一、知识链接
1.三角形的内角和为_______.
2.直角三角形有什么特点?
二、新知预习
1.如图,在△ABC中,已知∠C=90°.
△ABC叫做___________,用符号表示为__________;
∠A+∠B+∠C=_____°,∠A+∠B=_____°-∠C=_______°.
结论:直角三角形的两个锐角___________.
图
图
2.如图,在△ABC中,已知∠A+∠B=90°,
则∠C=_______°-(∠A+∠B)=_______°.
所以△ABC是_________.
结论:有两个角_______的三角形是直角三角形.
三、自学自测
1.在Rt△ABC中,∠B=90°,∠C=50°,则∠A=_______.
2.在△ABC中,若∠A=35°,∠C=55°,则△ABC是_________三角形.
四、我的疑惑
____________________________________________________________________________________________________________________________
(
教学备注
配套
PPT
讲授
1.情景引入
(见
幻灯片3-4
)
2.探究点1新知讲授
(见
幻灯片5-12
)
)
(
课堂探究
)
要点探究
探究点1:直角三角形的两个锐角互余
问题引导
问题1:如下图所示是我们常用的一副三角板,两锐角的度数之和为多少度?
问题2:如图,在Rt△ABC中,
∠C=90°,两锐角的和等于多少呢?
思考:由此,你可以得到直角三角形有什么性质呢?
总结归纳:
直角三角形的两个锐角___________.
应用格式:
在Rt△ABC
中,
∵ ∠C
=90°,
∴ ∠A
+∠B
=90°.
直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角三角形ABC
可以写成Rt△ABC
.
典例精析
例1:(1)如图,∠B=∠C=90°,AD交BC于点O,∠A与∠D有什么关系?
(2)如图,∠B=∠D=90°,AD交BC于点O,∠A与∠C有什么关系?请说明理由.
(
教学备注
3.探究点2新知讲授
(见
幻灯片13-16
)
)
图
图
例2:如图,
∠C=∠D=90
°,AD,BC相交于点E.
∠CAE与∠DBE有什么关系?为什么?
【变式题】如图,△ABC中,CD⊥AB于D,BE⊥AC于E,CD,BE相交于点F,∠A与∠BFC又有什么关系?为什么?
【总结归纳】
思考:通过前面的例题,你能画出这些题型的基本图形吗?
基本图形:
∠A=∠D
∠A=∠C
探究点2:有两个角互余的三角形是直角三角形
问题:有两个角互余的三角形是直角三角形吗?
如图,在△ABC中,
∠A
+∠B=90°
,
那么△ABC是直角三角形吗?
总结归纳:有两个角互余的三角形是直角三角形.
应用格式:
在△ABC
中,
∵∠A
+∠B
=90°,
∴△ABC
是直角三角形.
(
教学备注
配套
PPT
讲授
4.课堂小结(见
幻灯片21
)
5.当堂检测
(见
幻灯片17-20
)
)典例精析
例3:如图,∠C=90
°,
∠1=
∠2,△ADE是直角三角形吗?为什么?
例4:如图,CE⊥AD,垂足为E,∠A=∠C,△ABD是直角三角形吗?为什么?
二、课堂小结
直角三角形(表示:Rt△)
性质:直角三角形两锐角互余.
如图,若△ABC为直角三角形,且∠A为直角,则∠B+∠C=90°.
(
B
)
(
C
)
(
A
)
判定:有两个角互余的三角形为直角三角形.
如图,若∠B+∠C=90°,则△ABC为直角三角形.
(
教学备注
)
(
当堂检测
)
1.如图,一张长方形纸片,剪去一部分后得到一个三角形,则图中∠1+∠2的度数是________.
2.如图,AB、CD相交于点O,AC⊥CD于点C,若∠BOD=38°,则∠A=________.
3.在△ABC中,若∠A=43°,∠B=47°,则这个三角形是____________.
4.在一个直角三角形中,有一个锐角等于40°,则另一个锐角的度数是( )
A.40°
B.50°
C.60°
D.70°
5.具备下列条件的△ABC中,不是直角三角形的是
(
)
A.∠A+∠B=∠C
B.∠A-∠B=∠C
C.∠A:∠B:∠C=1:2:3
D.∠A=∠B=3∠C
6.如图所示,△ABC为直角三角形,∠ACB=90°,CD⊥AB,与∠1互余的角有( )
A.∠B
B.∠A
C.∠BCD和∠A
D.∠BCD
如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.
求证:△ACD是直角三角形.
参考答案
自主学习
一、知识链接
1.180°
2.直角三角形有一个内角是90°.
二、新知预习
1.(1)直角三角形
Rt△ABC
(2)180
90
90
互余
2.180
90
直角三角形
互余
三、自学自测
1.40°
2.直角
四、我的疑惑
课堂探究
要点探究
探究点1:直角三角形的两个锐角互余
问题引导
问题1
30°+60°=90°
45°+45°=90°
问题2
解:在Rt△ABC中,因为
∠C=90°,由三角形内角和定理,得∠A
+∠B+∠C=90°,即∠A
+∠B=90°.
总结归纳
互余
典例精析
例1
解:(1)方法一(利用平行的判定和性质):
∵∠B=∠C=90°,∴AB∥CD,∴∠A=∠D.
方法二(利用直角三角形的性质):
∵∠B=∠C=90°,∴∠A+∠AOB=90°,∠D+∠COD=90°.
∵∠AOB=∠COD,∴∠A=∠D.
(2)解:∠A=∠C.理由如下:
∵∠B=∠D=90°,∴∠A+∠AOB=90°,∠C+∠COD=90°.
∵∠AOB=∠COD,∴∠A=∠C.
例2
解:在Rt△ACE中,∠CAE=90
°-
∠AEC.
在Rt△BDE中,∠DBE=90
°-
∠BED.
∵∠AEC=
∠BED,∴∠CAE=
∠DBE.
【变式题】
解:∵CD⊥AB于点D,BE⊥AC于点E,
∴∠BEA=∠BDF=90°,∴∠ABE+∠A=90°,∠ABE+∠DFB=90°.
∴∠A=∠DFB.∵∠DFB+∠BFC=180°,∴∠A+∠BFC=180°.
探究点2:有两个角互余的三角形是直角三角形
问题
解:在△ABC中,因为
∠A
+∠B
+∠C=180°,
又∠A
+∠B=90°,所以∠C=90°.
于是△ABC是直角三角形.
典例精析
例3
解:在Rt△ABC中,∠2+
∠A=90
°.
∵
∠1=
∠2,
∴∠1
+
∠A=90
°.即△ADE是直角三角形.
例4
解:△ABD是直角三角形.理由如下:
∵CE⊥AD,∴∠CED=90°,∴∠C+∠D=90°.
∵∠A=∠C,∴∠A+∠D=90°,∴△ABD是直角三角形.
当堂检测
1.90°
2.52°
3.直角三角形
4.B
5.D
6.C
证明:∵∠ACB=90°,∴∠A+∠B=90°.
∵∠ACD=∠B,∴∠A+∠ACD=90°,∴△ACD是直角三角形.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
