人教版8年级数学(上册)同步课时导学案:12.1 全等三角形(含答案)
文档属性
| 名称 | 人教版8年级数学(上册)同步课时导学案:12.1 全等三角形(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
(
教学备注
学生在课前完成自主学习部分
1.情景引入
(见
幻灯片3-4
)
)第十二章
全等三角形
12.1
全等三角形
学习目标:1.了解全等形、全等三角形的概念,能正确识别全等三角形的对应元素.
2.掌握全等三角形对应边相等、对应角相等的性质.
3.能够利用全等三角形的性质解决一些简单的实际问题.
重点:全等三角形的性质.
难点:找全等三角形的对应边、对应角.
(
自主学习
)
一、知识链接
1.已知△ABC.
(1)画出△ABC向右平移1
cm后的△DEF.
(2)△ABC和△DEF的形状______,大小_______;对应点分别为__________________,对应边分别为_____________________,对应角分别为_______________________.
二、新知预习
1.观察下列一组图片,思考问题.
问题:图中有形状和大小都相同的图形吗?试把它们指出来.它们能够完全重合吗?你能再举出一些类似的例子吗?
2.自主归纳:
(1)能够完全重合的两个图形叫做________,则________________叫做全等三角形.
(2)“全等”符号:________读作“全等于”.
(3)全等三角形的性质:________________.
(4)如图:这两个三角形是完全重合的,则△ABC_____△A1B1C1.点A与A1点是对应顶点,点B与点___是对应顶点,点C与点___是对应顶点;对应边:________________;对应角:________________.
3.全等变换的方式有________,_______和________.
三、自学自测
如图,△OCA≌△OBD,C和B,A和D是对应顶点,则这两个三角
形中相等的边有
;相等的角有
;
有____个三角形,分别记作:_______________________.
(
教学备注
配套PPT
讲授
2.探究点1新知讲授
(见
幻灯片5-12
)
)四、我的疑惑
____________________________________________________________________________________________________________________________________________________
(
课堂探究
)
要点探究
探究点1:全等三角形的定义及性质
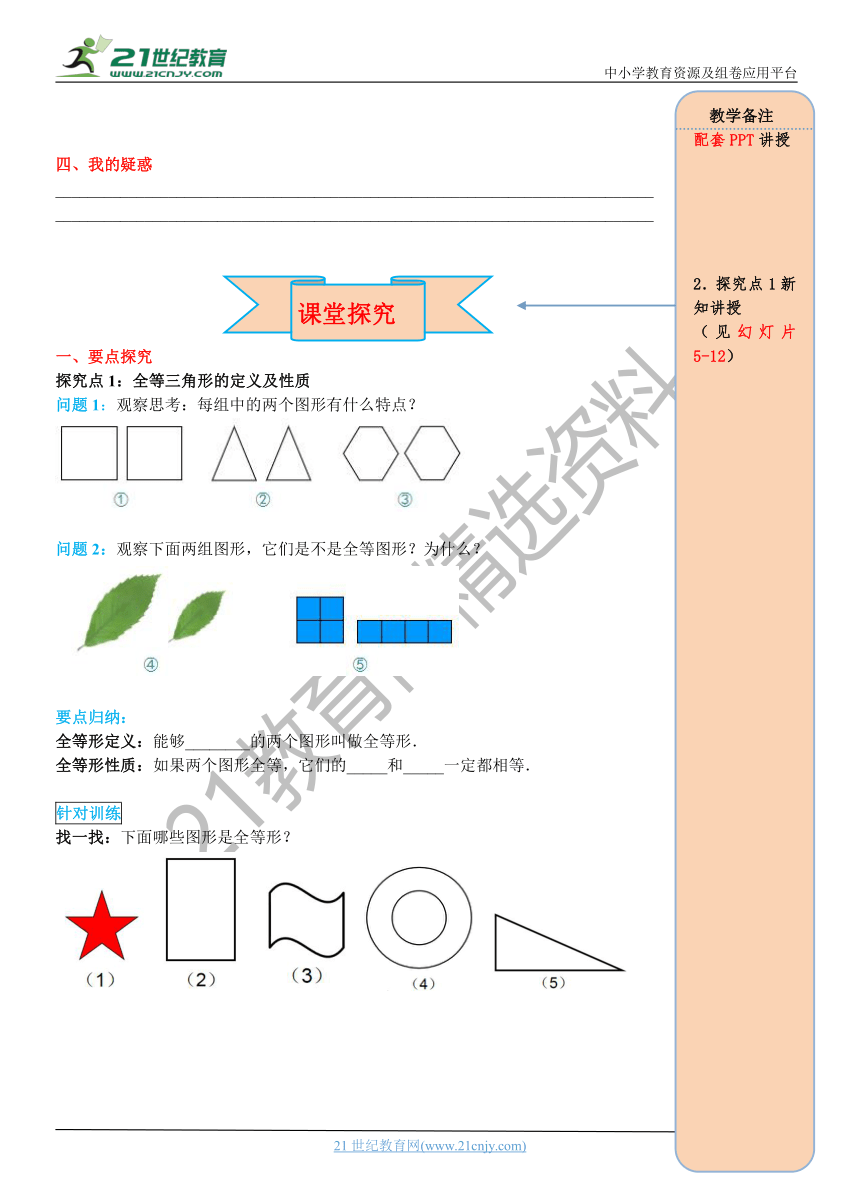
问题1:观察思考:每组中的两个图形有什么特点?
问题2:观察下面两组图形,它们是不是全等图形?为什么?
要点归纳:
全等形定义:能够________的两个图形叫做全等形.
全等形性质:如果两个图形全等,它们的_____和_____一定都相等.
针对训练
找一找:下面哪些图形是全等形?
(
教学备注
)
要点归纳:
全等三角形:
能够完全重合的两个三角形叫_______________.
全等三角形的对应元素:
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
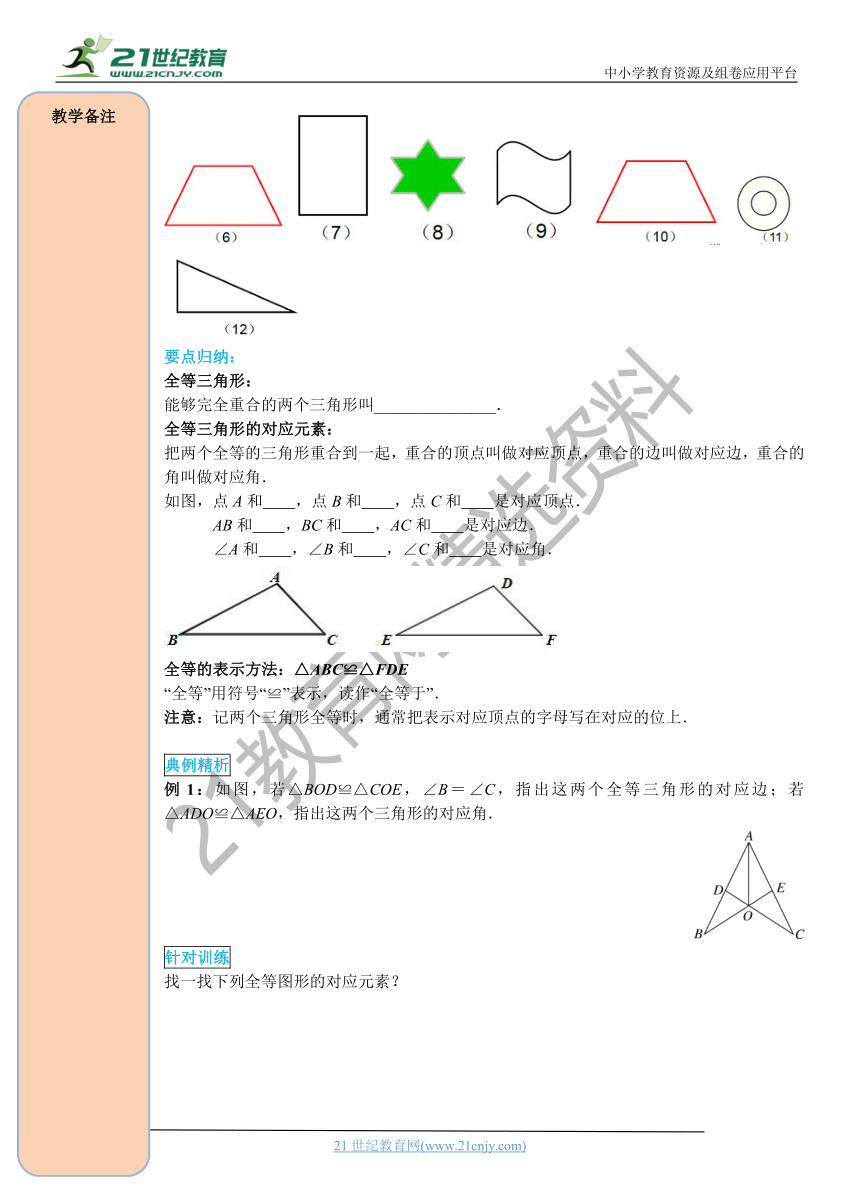
如图,点A和
,点B和
,点C和
是对应顶点.
AB和
,BC和
,AC和
是对应边.
∠A和
,∠B和
,∠C和
是对应角.
全等的表示方法:△ABC≌△FDE
“全等”用符号“≌”表示,读作“全等于”.
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位上.
典例精析
例1:如图,若△BOD≌△COE,∠B=∠C,指出这两个全等三角形的对应边;若△ADO≌△AEO,指出这两个三角形的对应角.
针对训练
找一找下列全等图形的对应元素?
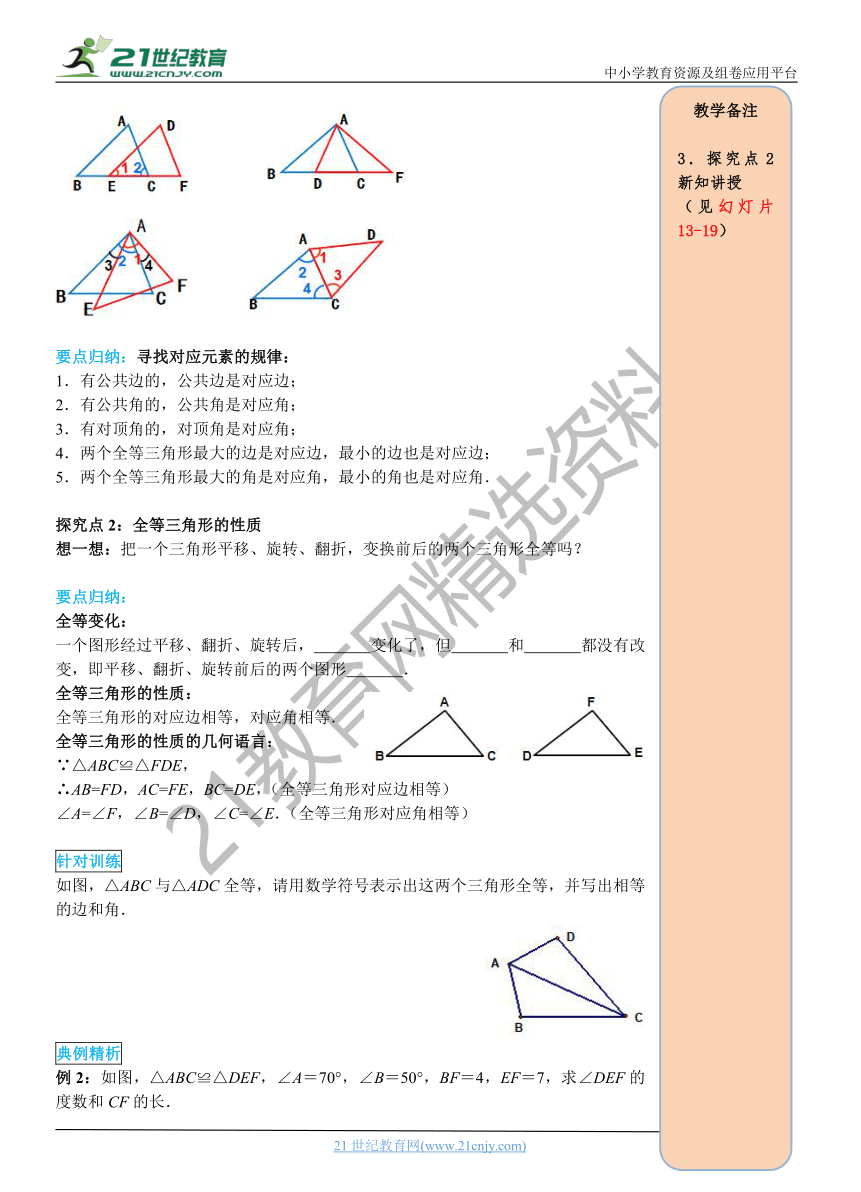
要点归纳:寻找对应元素的规律:
1.有公共边的,公共边是对应边;
2.有公共角的,公共角是对应角;
3.有对顶角的,对顶角是对应角;
4.两个全等三角形最大的边是对应边,最小的边也是对应边;
5.两个全等三角形最大的角是对应角,最小的角也是对应角.
(
教学备注
3.探究点2新知讲授
(见
幻灯片13-19
)
)探究点2:全等三角形的性质
想一想:把一个三角形平移、旋转、翻折,变换前后的两个三角形全等吗?
要点归纳:
全等变化:
一个图形经过平移、翻折、旋转后,
变化了,但
和
都没有改变,即平移、翻折、旋转前后的两个图形
.
全等三角形的性质:
全等三角形的对应边相等,对应角相等.
全等三角形的性质的几何语言:
∵△ABC≌△FDE,
∴AB=FD,AC=FE,BC=DE,(全等三角形对应边相等)
∠A=∠F,∠B=∠D,∠C=∠E.(全等三角形对应角相等)
针对训练
如图,△ABC与△ADC全等,请用数学符号表示出这两个三角形全等,并写出相等的边和角.
典例精析
例2:如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠DEF的度数和CF的长.
(
教学备注
配套PPT
讲授
5.课堂小结
(见
幻灯片29
)
6.当堂检测
(见
幻灯片20-28
)
)
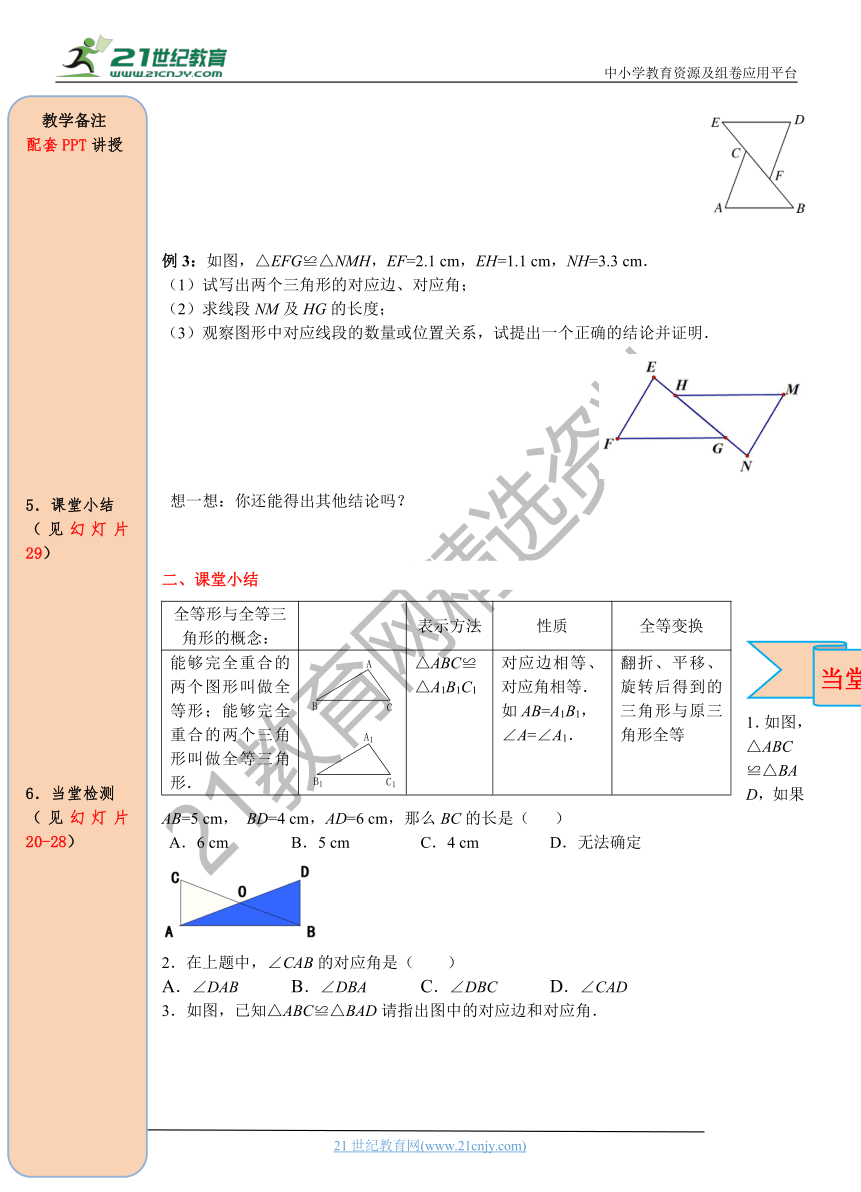
例3:如图,△EFG≌△NMH,EF=2.1
cm,EH=1.1
cm,NH=3.3
cm.
(1)试写出两个三角形的对应边、对应角;
(2)求线段NM及HG的长度;
(3)观察图形中对应线段的数量或位置关系,试提出一个正确的结论并证明.
想一想:你还能得出其他结论吗?
二、课堂小结
全等形与全等三角形的概念:
表示方法
性质
全等变换
能够完全重合的两个图形叫做全等形;能够完全重合的两个三角形叫做全等三角形.
△ABC≌△A1B1C1
对应边相等、对应角相等.
如AB=A1B1,
∠A=∠A1.
翻折、平移、旋转后得到的三角形与原三角形全等
(
当堂检测
)
1.如图,△ABC≌△BAD,如果AB=5
cm,
BD=4
cm,AD=6
cm,那么BC的长是(
)
A.6
cm
B.5
cm
C.4
cm
D.无法确定
2.在上题中,∠CAB的对应角是(
)
A.∠DAB
B.∠DBA
C.∠DBC
D.∠CAD
3.如图,已知△ABC≌△BAD请指出图中的对应边和对应角.
变式:如图:平移后△ABC≌△EFD,若AB=6,AE=2.
你能求出AF的长吗?说说你的理由.
解:∵△
≌△
,
∴AB=
=
,
∴AB-
=EF-
.
∴AF=EB=
.
(
教学备注
配套PPT
讲授
)4.如图,已知△ABC≌△AED,请指出图中对应边和对应角.
变式:如图,已知△ABC≌△AED,若AB=6,AC=2,∠B=25°,你还能说出△ADE中其他角的大小和边的长度吗?
5.如图,长方形ABCD沿AM折叠,使D点落在BC上的N点处,AD=7
cm,DM=5
cm,∠DAM=39°,则△ANM≌△ADM,AN=
cm,NM=
cm,∠NAB=
.
6.如图△ABC≌△DEF,边AB和DE在同一条直线上,试说明图中有哪些线段平行,并
说明理由.
摆一摆:利用平移,翻折,旋转等变换所得到的三角形与原三角形组成各种各样新的图形,你还能拼出什么不同的造型吗?比一比看谁更有创意!
参考答案
自主学习
一、知识链接
1.(1)图略.
(2)相同
相等
点A和点D,点B和点E,点C和点F
AB和DE,BC和EF,AC和DF
∠A和∠D,∠B和∠E,∠C和∠F
二、新知预习
1.略
2.(1)全等形
能够完全重合的两个三角形
(2)≌
(3)全等三角形的对应边相等,全等三角形的对应角相等
(4)≌
B1
C1
AB和A1B1,BC和B1C1,AC和A1C1
∠A和∠A1,∠B和∠B1,∠C和∠C1
3.平移
翻折
旋转
三、自学自测
AC和DB,OC和OB,OA和OD
∠A和∠D,∠C和∠B,∠AOC和∠DOB
两
△OCA,△OBD
课堂探究
要点探究
探究点1:全等三角形的定义及性质
问题1
每组中的两个图形的形状、大小相等.
问题2
它们不是全等图形,因为它们的形状和大小都不相等.
要点归纳
完全重合
形状
大小
针对训练
找一找
(2)和(7),(3)和(9),(5)和(12),(6)和(10)
要点归纳
全等三角形
点D
点E
点F
DE
EF
DF
∠D
∠E
∠F
典例精析
例1
解:△BOD与△COE的对应边为:BO与CO,OD与OE,BD与CE;
△ADO与△AEO的对应角为:∠DAO与∠EAO,∠ADO与∠AEO,∠AOD与∠AOE.
探究点2:全等三角形的性质
要点归纳
位置
形状
大小
全等
针对训练
解:△ABC≌△ADC;
相等的边为:AB=AD,AC=AC,BC=DC;
相等的角为:∠BAC=∠DAC,∠B=∠D,∠ACB=∠ACD.
典例精析
例2
解:∵△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,
∴∠DEF=∠B=50°,BC=EF=7,∴CF=BC-BF=7-4=3.
例3
解:(1)对应边有EF和NM,FG和MH,EG和NH;
对应角有∠E和∠N,∠F和∠M,∠EGF和∠NHM.
(2)∵△EFG≌△NMH,∴NM=EF=2.1
cm,EG=NH=3.3
cm.∴HG=EG–EH=3.3-1.1=2.2(cm).
(3)结论:EF∥NM.证明如下:∵△EFG≌△NMH,∴∠E=∠N.∴EF∥NM.
当堂检测
1.A
2.B
3.BA
BD
AD
∠ABD
∠BAD
∠D
变式:ABC
EFD
EF
6
AE
AE
6-2
4
4.AE
AD
ED
∠A
∠E
∠ADE
变式:解:∵△ABC≌△AED,
∴∠E=∠B=25°(全等三角形对应角相等),
AD=AC=2,AE=AB=6(全等三角形对应边相等).
5.7
5
12°
6.解:AC∥DF,BC∥EF.理由如下:
∵△ABC≌△DEF,∴∠A=∠2,∠1=∠E,(全等三角形对应角相等)
摆一摆:
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
(
教学备注
学生在课前完成自主学习部分
1.情景引入
(见
幻灯片3-4
)
)第十二章
全等三角形
12.1
全等三角形
学习目标:1.了解全等形、全等三角形的概念,能正确识别全等三角形的对应元素.
2.掌握全等三角形对应边相等、对应角相等的性质.
3.能够利用全等三角形的性质解决一些简单的实际问题.
重点:全等三角形的性质.
难点:找全等三角形的对应边、对应角.
(
自主学习
)
一、知识链接
1.已知△ABC.
(1)画出△ABC向右平移1
cm后的△DEF.
(2)△ABC和△DEF的形状______,大小_______;对应点分别为__________________,对应边分别为_____________________,对应角分别为_______________________.
二、新知预习
1.观察下列一组图片,思考问题.
问题:图中有形状和大小都相同的图形吗?试把它们指出来.它们能够完全重合吗?你能再举出一些类似的例子吗?
2.自主归纳:
(1)能够完全重合的两个图形叫做________,则________________叫做全等三角形.
(2)“全等”符号:________读作“全等于”.
(3)全等三角形的性质:________________.
(4)如图:这两个三角形是完全重合的,则△ABC_____△A1B1C1.点A与A1点是对应顶点,点B与点___是对应顶点,点C与点___是对应顶点;对应边:________________;对应角:________________.
3.全等变换的方式有________,_______和________.
三、自学自测
如图,△OCA≌△OBD,C和B,A和D是对应顶点,则这两个三角
形中相等的边有
;相等的角有
;
有____个三角形,分别记作:_______________________.
(
教学备注
配套PPT
讲授
2.探究点1新知讲授
(见
幻灯片5-12
)
)四、我的疑惑
____________________________________________________________________________________________________________________________________________________
(
课堂探究
)
要点探究
探究点1:全等三角形的定义及性质
问题1:观察思考:每组中的两个图形有什么特点?
问题2:观察下面两组图形,它们是不是全等图形?为什么?
要点归纳:
全等形定义:能够________的两个图形叫做全等形.
全等形性质:如果两个图形全等,它们的_____和_____一定都相等.
针对训练
找一找:下面哪些图形是全等形?
(
教学备注
)
要点归纳:
全等三角形:
能够完全重合的两个三角形叫_______________.
全等三角形的对应元素:
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
如图,点A和
,点B和
,点C和
是对应顶点.
AB和
,BC和
,AC和
是对应边.
∠A和
,∠B和
,∠C和
是对应角.
全等的表示方法:△ABC≌△FDE
“全等”用符号“≌”表示,读作“全等于”.
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位上.
典例精析
例1:如图,若△BOD≌△COE,∠B=∠C,指出这两个全等三角形的对应边;若△ADO≌△AEO,指出这两个三角形的对应角.
针对训练
找一找下列全等图形的对应元素?
要点归纳:寻找对应元素的规律:
1.有公共边的,公共边是对应边;
2.有公共角的,公共角是对应角;
3.有对顶角的,对顶角是对应角;
4.两个全等三角形最大的边是对应边,最小的边也是对应边;
5.两个全等三角形最大的角是对应角,最小的角也是对应角.
(
教学备注
3.探究点2新知讲授
(见
幻灯片13-19
)
)探究点2:全等三角形的性质
想一想:把一个三角形平移、旋转、翻折,变换前后的两个三角形全等吗?
要点归纳:
全等变化:
一个图形经过平移、翻折、旋转后,
变化了,但
和
都没有改变,即平移、翻折、旋转前后的两个图形
.
全等三角形的性质:
全等三角形的对应边相等,对应角相等.
全等三角形的性质的几何语言:
∵△ABC≌△FDE,
∴AB=FD,AC=FE,BC=DE,(全等三角形对应边相等)
∠A=∠F,∠B=∠D,∠C=∠E.(全等三角形对应角相等)
针对训练
如图,△ABC与△ADC全等,请用数学符号表示出这两个三角形全等,并写出相等的边和角.
典例精析
例2:如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠DEF的度数和CF的长.
(
教学备注
配套PPT
讲授
5.课堂小结
(见
幻灯片29
)
6.当堂检测
(见
幻灯片20-28
)
)
例3:如图,△EFG≌△NMH,EF=2.1
cm,EH=1.1
cm,NH=3.3
cm.
(1)试写出两个三角形的对应边、对应角;
(2)求线段NM及HG的长度;
(3)观察图形中对应线段的数量或位置关系,试提出一个正确的结论并证明.
想一想:你还能得出其他结论吗?
二、课堂小结
全等形与全等三角形的概念:
表示方法
性质
全等变换
能够完全重合的两个图形叫做全等形;能够完全重合的两个三角形叫做全等三角形.
△ABC≌△A1B1C1
对应边相等、对应角相等.
如AB=A1B1,
∠A=∠A1.
翻折、平移、旋转后得到的三角形与原三角形全等
(
当堂检测
)
1.如图,△ABC≌△BAD,如果AB=5
cm,
BD=4
cm,AD=6
cm,那么BC的长是(
)
A.6
cm
B.5
cm
C.4
cm
D.无法确定
2.在上题中,∠CAB的对应角是(
)
A.∠DAB
B.∠DBA
C.∠DBC
D.∠CAD
3.如图,已知△ABC≌△BAD请指出图中的对应边和对应角.
变式:如图:平移后△ABC≌△EFD,若AB=6,AE=2.
你能求出AF的长吗?说说你的理由.
解:∵△
≌△
,
∴AB=
=
,
∴AB-
=EF-
.
∴AF=EB=
.
(
教学备注
配套PPT
讲授
)4.如图,已知△ABC≌△AED,请指出图中对应边和对应角.
变式:如图,已知△ABC≌△AED,若AB=6,AC=2,∠B=25°,你还能说出△ADE中其他角的大小和边的长度吗?
5.如图,长方形ABCD沿AM折叠,使D点落在BC上的N点处,AD=7
cm,DM=5
cm,∠DAM=39°,则△ANM≌△ADM,AN=
cm,NM=
cm,∠NAB=
.
6.如图△ABC≌△DEF,边AB和DE在同一条直线上,试说明图中有哪些线段平行,并
说明理由.
摆一摆:利用平移,翻折,旋转等变换所得到的三角形与原三角形组成各种各样新的图形,你还能拼出什么不同的造型吗?比一比看谁更有创意!
参考答案
自主学习
一、知识链接
1.(1)图略.
(2)相同
相等
点A和点D,点B和点E,点C和点F
AB和DE,BC和EF,AC和DF
∠A和∠D,∠B和∠E,∠C和∠F
二、新知预习
1.略
2.(1)全等形
能够完全重合的两个三角形
(2)≌
(3)全等三角形的对应边相等,全等三角形的对应角相等
(4)≌
B1
C1
AB和A1B1,BC和B1C1,AC和A1C1
∠A和∠A1,∠B和∠B1,∠C和∠C1
3.平移
翻折
旋转
三、自学自测
AC和DB,OC和OB,OA和OD
∠A和∠D,∠C和∠B,∠AOC和∠DOB
两
△OCA,△OBD
课堂探究
要点探究
探究点1:全等三角形的定义及性质
问题1
每组中的两个图形的形状、大小相等.
问题2
它们不是全等图形,因为它们的形状和大小都不相等.
要点归纳
完全重合
形状
大小
针对训练
找一找
(2)和(7),(3)和(9),(5)和(12),(6)和(10)
要点归纳
全等三角形
点D
点E
点F
DE
EF
DF
∠D
∠E
∠F
典例精析
例1
解:△BOD与△COE的对应边为:BO与CO,OD与OE,BD与CE;
△ADO与△AEO的对应角为:∠DAO与∠EAO,∠ADO与∠AEO,∠AOD与∠AOE.
探究点2:全等三角形的性质
要点归纳
位置
形状
大小
全等
针对训练
解:△ABC≌△ADC;
相等的边为:AB=AD,AC=AC,BC=DC;
相等的角为:∠BAC=∠DAC,∠B=∠D,∠ACB=∠ACD.
典例精析
例2
解:∵△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,
∴∠DEF=∠B=50°,BC=EF=7,∴CF=BC-BF=7-4=3.
例3
解:(1)对应边有EF和NM,FG和MH,EG和NH;
对应角有∠E和∠N,∠F和∠M,∠EGF和∠NHM.
(2)∵△EFG≌△NMH,∴NM=EF=2.1
cm,EG=NH=3.3
cm.∴HG=EG–EH=3.3-1.1=2.2(cm).
(3)结论:EF∥NM.证明如下:∵△EFG≌△NMH,∴∠E=∠N.∴EF∥NM.
当堂检测
1.A
2.B
3.BA
BD
AD
∠ABD
∠BAD
∠D
变式:ABC
EFD
EF
6
AE
AE
6-2
4
4.AE
AD
ED
∠A
∠E
∠ADE
变式:解:∵△ABC≌△AED,
∴∠E=∠B=25°(全等三角形对应角相等),
AD=AC=2,AE=AB=6(全等三角形对应边相等).
5.7
5
12°
6.解:AC∥DF,BC∥EF.理由如下:
∵△ABC≌△DEF,∴∠A=∠2,∠1=∠E,(全等三角形对应角相等)
摆一摆:
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
