内蒙古赤峰市2020-2021学年高一下学期期末考试数学(文)试题(B)(Word版含答案)
文档属性
| 名称 | 内蒙古赤峰市2020-2021学年高一下学期期末考试数学(文)试题(B)(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 699.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 00:00:00 | ||
图片预览




文档简介
2021年赤峰市普通高中联考高一年级
文科数学试题(B)
一?选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
设集合,,则(
)
A.
B.
C.
D.
2.
不等式的解集是(
)
A.
B.
C.
D.
3.
已知,则等于
A.
1
B.
3
C.
15
D.
30
4.
已知等比数列,,则等于(
)
A.
35
B.
63
C.
D.
189
5.
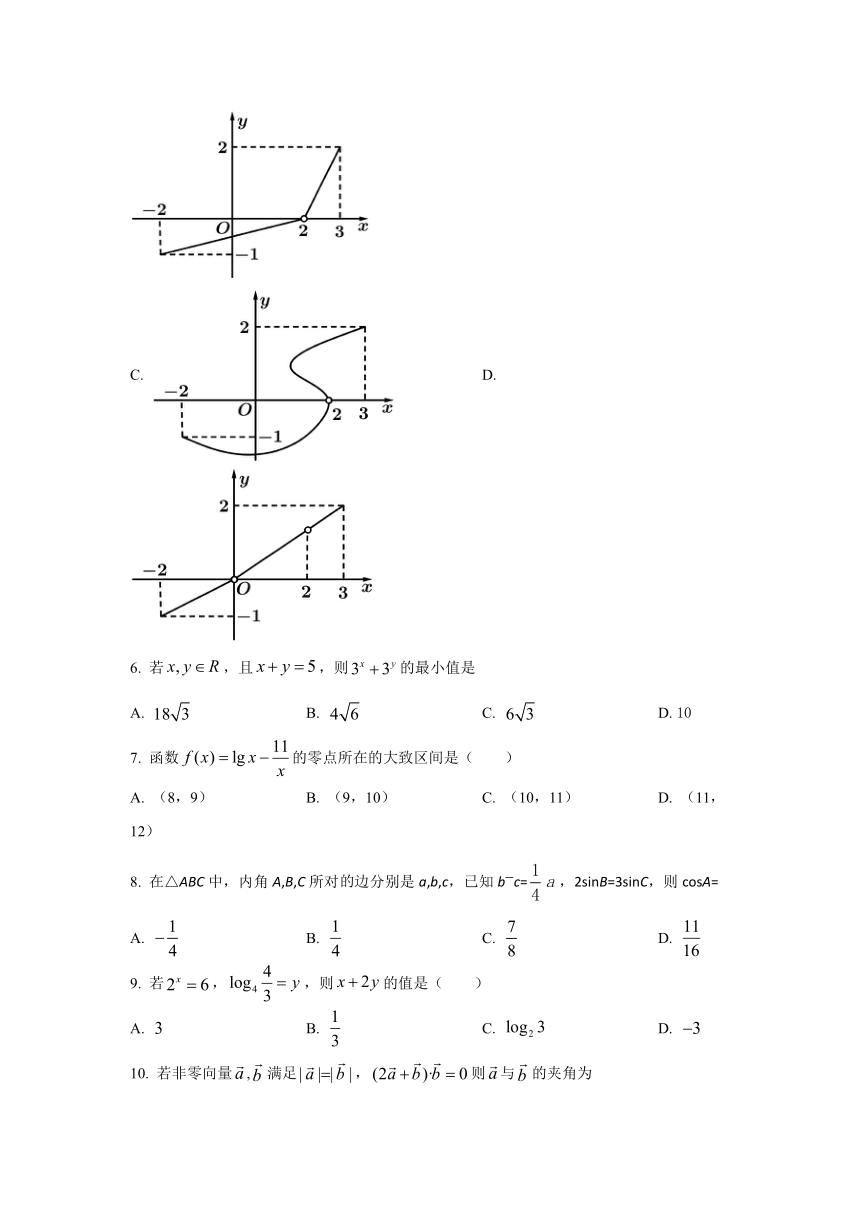
若函数y=f(x)的定义域为,且,值域为,且,则y=f(x)的图象可能是(
)
A.
B.
C.
D.
6.
若,且,则的最小值是
A.
B.
C.
D.
10
7.
函数的零点所在的大致区间是(
)
A.
(8,9)
B.
(9,10)
C.
(10,11)
D.
(11,12)
8.
在△ABC中,内角A,B,C所对边分别是a,b,c,已知bc=,2sinB=3sinC,则cosA=
A.
B.
C.
D.
9.
若,,则的值是(
)
A.
B.
C.
D.
10.
若非零向量,满足,则与的夹角为
A
B.
C.
D.
11.
是
A.
最小正周期为的偶函数
B.
最小正周期为的奇函数
C.
最小正周期为的偶函数
D.
最小正周期为的奇函数
12.
若函数是R上的增函数,则a的取值范围为(
)
A.
B.
C.
D.
二?填空题:本题共4小题,每题5分,共20分.请将答案填在答题卡对应题号的位置上.
13.
函数的定义域为___________.
14.
如图,若一个水平放置的平面图形的斜二测直观图是一个底角为,且腰和上底均为的等腰梯形,则原平面图形的面积是________.
15.
若平面向量,则在上的投影为___________.
16.
正四棱锥S-ABCD的侧棱长为,底面边长为,E为SA的中点,则异面直线BE和SC所成的角为___________.
三?解答题:共6小题,共70分.解答应写出文字说明?演算步骤或证明过程.
17.
函数,图象如图所示,为常数,
(1)求函数f(x)的解析式;
(2)求的值.
18.
在中,角
的对边分别为
,
,
,
的面积为
.
(1)求的值;
(2)求的值.
19.
如图,底面是正三角形的直三棱柱中,是的中点,.
(1)求证:平面;
(2)求三棱锥的体积.
20.
已知等差数列的公差不为零,,且成等比数列.
(1)求的通项公式
(2)求.
21.
甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品(百台),其总成本为(万元),其中固定成本为万元,并且每生产百台的生产成本为万元(总成本固定成本生产成本),销售收入,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数的解析式(利润销售收入总成本);
(2)甲厂生产多少台新产品时,可使盈利最多?
22
已知函数.
(1)求函数f(x)在区间上最值;
(2)若关于x的方程(x+2)f(x)-ax=0在区间(0,3)内有两个不等实根,求实数a的取值范围.
2021年赤峰市普通高中联考高一年级
文科数学试题(B)
答案版
一?选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
设集合,,则(
)
A.
B.
C.
D.
答案:B
2.
不等式的解集是(
)
A.
B.
C.
D.
答案:C
3.
已知,则等于
A.
1
B.
3
C.
15
D.
30
答案:C
4.
已知等比数列,,则等于(
)
A.
35
B.
63
C.
D.
189
答案:D
5.
若函数y=f(x)的定义域为,且,值域为,且,则y=f(x)的图象可能是(
)
A.
B.
C.
D.
答案:B
6.
若,且,则的最小值是
A.
B.
C.
D.
10
答案:A
7.
函数的零点所在的大致区间是(
)
A.
(8,9)
B.
(9,10)
C.
(10,11)
D.
(11,12)
答案:C
8.
在△ABC中,内角A,B,C所对边分别是a,b,c,已知bc=,2sinB=3sinC,则cosA=
A.
B.
C.
D.
答案:A
9.
若,,则的值是(
)
A.
B.
C.
D.
答案:A
10.
若非零向量,满足,则与的夹角为
A
B.
C.
D.
答案:C
11.
是
A.
最小正周期为的偶函数
B.
最小正周期为的奇函数
C.
最小正周期为的偶函数
D.
最小正周期为的奇函数
答案:D
12.
若函数是R上的增函数,则a的取值范围为(
)
A.
B.
C.
D.
答案:B
二?填空题:本题共4小题,每题5分,共20分.请将答案填在答题卡对应题号的位置上.
13.
函数的定义域为___________.
答案:
14.
如图,若一个水平放置的平面图形的斜二测直观图是一个底角为,且腰和上底均为的等腰梯形,则原平面图形的面积是________.
答案:
15.
若平面向量,则在上的投影为___________.
答案:
16.
正四棱锥S-ABCD的侧棱长为,底面边长为,E为SA的中点,则异面直线BE和SC所成的角为___________.
答案:
三?解答题:共6小题,共70分.解答应写出文字说明?演算步骤或证明过程.
17.
函数,图象如图所示,为常数,
(1)求函数f(x)的解析式;
(2)求的值.
答案:(1);(2).
18.
在中,角
的对边分别为
,
,
,
的面积为
.
(1)求的值;
(2)求的值.
答案:
19.
如图,底面是正三角形的直三棱柱中,是的中点,.
(1)求证:平面;
(2)求三棱锥的体积.
答案:(1)证明见解析;(2).
20.
已知等差数列的公差不为零,,且成等比数列.
(1)求的通项公式
(2)求.
答案:(1);(2)
21.
甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品(百台),其总成本为(万元),其中固定成本为万元,并且每生产百台的生产成本为万元(总成本固定成本生产成本),销售收入,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数的解析式(利润销售收入总成本);
(2)甲厂生产多少台新产品时,可使盈利最多?
答案:(1);(2)当甲厂生产百台时,可使盈利最多.
22
已知函数.
(1)求函数f(x)在区间上最值;
(2)若关于x的方程(x+2)f(x)-ax=0在区间(0,3)内有两个不等实根,求实数a的取值范围.
答案:(1)最大值为3,最小值为2;(2)
文科数学试题(B)
一?选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
设集合,,则(
)
A.
B.
C.
D.
2.
不等式的解集是(
)
A.
B.
C.
D.
3.
已知,则等于
A.
1
B.
3
C.
15
D.
30
4.
已知等比数列,,则等于(
)
A.
35
B.
63
C.
D.
189
5.
若函数y=f(x)的定义域为,且,值域为,且,则y=f(x)的图象可能是(
)
A.
B.
C.
D.
6.
若,且,则的最小值是
A.
B.
C.
D.
10
7.
函数的零点所在的大致区间是(
)
A.
(8,9)
B.
(9,10)
C.
(10,11)
D.
(11,12)
8.
在△ABC中,内角A,B,C所对边分别是a,b,c,已知bc=,2sinB=3sinC,则cosA=
A.
B.
C.
D.
9.
若,,则的值是(
)
A.
B.
C.
D.
10.
若非零向量,满足,则与的夹角为
A
B.
C.
D.
11.
是
A.
最小正周期为的偶函数
B.
最小正周期为的奇函数
C.
最小正周期为的偶函数
D.
最小正周期为的奇函数
12.
若函数是R上的增函数,则a的取值范围为(
)
A.
B.
C.
D.
二?填空题:本题共4小题,每题5分,共20分.请将答案填在答题卡对应题号的位置上.
13.
函数的定义域为___________.
14.
如图,若一个水平放置的平面图形的斜二测直观图是一个底角为,且腰和上底均为的等腰梯形,则原平面图形的面积是________.
15.
若平面向量,则在上的投影为___________.
16.
正四棱锥S-ABCD的侧棱长为,底面边长为,E为SA的中点,则异面直线BE和SC所成的角为___________.
三?解答题:共6小题,共70分.解答应写出文字说明?演算步骤或证明过程.
17.
函数,图象如图所示,为常数,
(1)求函数f(x)的解析式;
(2)求的值.
18.
在中,角
的对边分别为
,
,
,
的面积为
.
(1)求的值;
(2)求的值.
19.
如图,底面是正三角形的直三棱柱中,是的中点,.
(1)求证:平面;
(2)求三棱锥的体积.
20.
已知等差数列的公差不为零,,且成等比数列.
(1)求的通项公式
(2)求.
21.
甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品(百台),其总成本为(万元),其中固定成本为万元,并且每生产百台的生产成本为万元(总成本固定成本生产成本),销售收入,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数的解析式(利润销售收入总成本);
(2)甲厂生产多少台新产品时,可使盈利最多?
22
已知函数.
(1)求函数f(x)在区间上最值;
(2)若关于x的方程(x+2)f(x)-ax=0在区间(0,3)内有两个不等实根,求实数a的取值范围.
2021年赤峰市普通高中联考高一年级
文科数学试题(B)
答案版
一?选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
设集合,,则(
)
A.
B.
C.
D.
答案:B
2.
不等式的解集是(
)
A.
B.
C.
D.
答案:C
3.
已知,则等于
A.
1
B.
3
C.
15
D.
30
答案:C
4.
已知等比数列,,则等于(
)
A.
35
B.
63
C.
D.
189
答案:D
5.
若函数y=f(x)的定义域为,且,值域为,且,则y=f(x)的图象可能是(
)
A.
B.
C.
D.
答案:B
6.
若,且,则的最小值是
A.
B.
C.
D.
10
答案:A
7.
函数的零点所在的大致区间是(
)
A.
(8,9)
B.
(9,10)
C.
(10,11)
D.
(11,12)
答案:C
8.
在△ABC中,内角A,B,C所对边分别是a,b,c,已知bc=,2sinB=3sinC,则cosA=
A.
B.
C.
D.
答案:A
9.
若,,则的值是(
)
A.
B.
C.
D.
答案:A
10.
若非零向量,满足,则与的夹角为
A
B.
C.
D.
答案:C
11.
是
A.
最小正周期为的偶函数
B.
最小正周期为的奇函数
C.
最小正周期为的偶函数
D.
最小正周期为的奇函数
答案:D
12.
若函数是R上的增函数,则a的取值范围为(
)
A.
B.
C.
D.
答案:B
二?填空题:本题共4小题,每题5分,共20分.请将答案填在答题卡对应题号的位置上.
13.
函数的定义域为___________.
答案:
14.
如图,若一个水平放置的平面图形的斜二测直观图是一个底角为,且腰和上底均为的等腰梯形,则原平面图形的面积是________.
答案:
15.
若平面向量,则在上的投影为___________.
答案:
16.
正四棱锥S-ABCD的侧棱长为,底面边长为,E为SA的中点,则异面直线BE和SC所成的角为___________.
答案:
三?解答题:共6小题,共70分.解答应写出文字说明?演算步骤或证明过程.
17.
函数,图象如图所示,为常数,
(1)求函数f(x)的解析式;
(2)求的值.
答案:(1);(2).
18.
在中,角
的对边分别为
,
,
,
的面积为
.
(1)求的值;
(2)求的值.
答案:
19.
如图,底面是正三角形的直三棱柱中,是的中点,.
(1)求证:平面;
(2)求三棱锥的体积.
答案:(1)证明见解析;(2).
20.
已知等差数列的公差不为零,,且成等比数列.
(1)求的通项公式
(2)求.
答案:(1);(2)
21.
甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品(百台),其总成本为(万元),其中固定成本为万元,并且每生产百台的生产成本为万元(总成本固定成本生产成本),销售收入,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数的解析式(利润销售收入总成本);
(2)甲厂生产多少台新产品时,可使盈利最多?
答案:(1);(2)当甲厂生产百台时,可使盈利最多.
22
已知函数.
(1)求函数f(x)在区间上最值;
(2)若关于x的方程(x+2)f(x)-ax=0在区间(0,3)内有两个不等实根,求实数a的取值范围.
答案:(1)最大值为3,最小值为2;(2)
同课章节目录
