人教版八年级数学上册 第十二章全等三角形 12.1 全等三角形导学案(有答案)
文档属性
| 名称 | 人教版八年级数学上册 第十二章全等三角形 12.1 全等三角形导学案(有答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 37.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 00:00:00 | ||
图片预览

文档简介
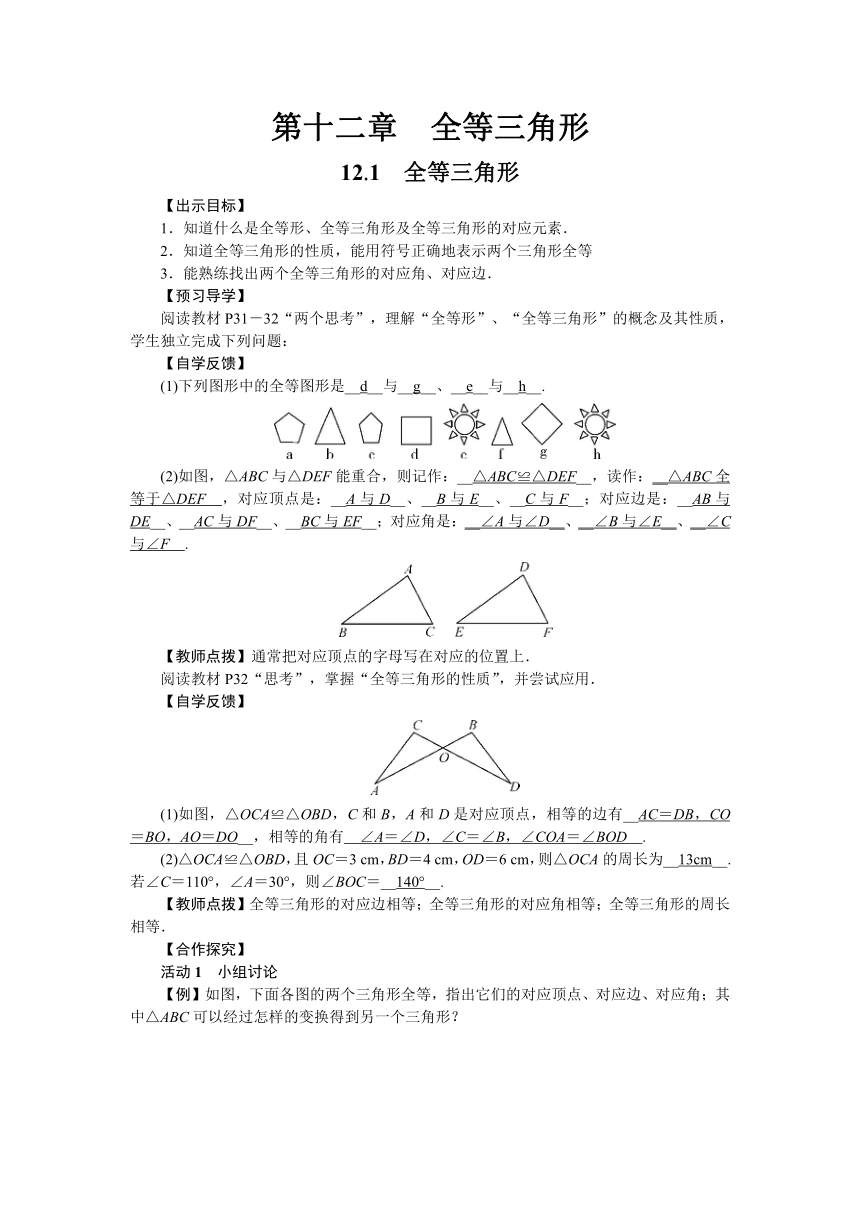
第十二章 全等三角形
12.1 全等三角形
【出示目标】
1.知道什么是全等形、全等三角形及全等三角形的对应元素.
2.知道全等三角形的性质,能用符号正确地表示两个三角形全等
3.能熟练找出两个全等三角形的对应角、对应边.
【预习导学】
阅读教材P31-32“两个思考”,理解“全等形”、“全等三角形”的概念及其性质,学生独立完成下列问题:
【自学反馈】
(1)下列图形中的全等图形是__d__与__g__、__e__与__h__.
(2)如图,△ABC与△DEF能重合,则记作:__△ABC≌△DEF__,读作:__△ABC全等于△DEF
,对应顶点是:__A与D__、__B与E__、__C与F__;对应边是:__AB与DE__、__AC与DF__、__BC与EF__;对应角是:__∠A与∠D__、__∠B与∠E__、__∠C与∠F
.
【教师点拨】通常把对应顶点的字母写在对应的位置上.
阅读教材P32“思考”,掌握“全等三角形的性质”,并尝试应用.
【自学反馈】
(1)如图,△OCA≌△OBD,C和B,A和D是对应顶点,相等的边有__AC=DB,CO=BO,AO=DO__,相等的角有
∠A=∠D,∠C=∠B,∠COA=∠BOD
.
(2)△OCA≌△OBD,且OC=3
cm,BD=4
cm,OD=6
cm,则△OCA的周长为__13cm__.若∠C=110°,∠A=30°,则∠BOC=__140°__.
【教师点拨】全等三角形的对应边相等;全等三角形的对应角相等;全等三角形的周长相等.
【合作探究】
活动1 小组讨论
【例】如图,下面各图的两个三角形全等,指出它们的对应顶点、对应边、对应角;其中△ABC可以经过怎样的变换得到另一个三角形?
图甲 图乙 图丙
解:甲:对应顶点是点A与点D,点B与点E,点C与点F;
对应边是AB与DE,AC与DF,BC与EF;
对应角是∠A与∠D,∠B与∠E,∠C与∠F;
△ABC经过平移得到另一个三角形.
乙:对应顶点是点A与点D,点B与点B,点C与点C;
对应边是AB与DB,AC与DC,BC与BC;
对应角是∠A与∠D,∠ABC与∠DBC,∠ACB与∠DCB;
△ABC经过向下翻折得到另一个三角形.
丙:对应顶点是点D与点C,点A与点A,点E与点B;
对应边是AD与AC,AE与AB,DE与CB;
对应角是∠D与∠C,∠E与∠B,∠DAE与∠CAB;
△ABC经过旋转得到另一个三角形.
【教师点拨】一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,所以平移、翻折、旋转前后的图形全等,这也是我们通过运动的方法寻求全等的一种策略.
活动2 跟踪训练
1.如图,已知△ABE≌△ACD,∠ADE=∠AED,∠B=∠C,指出其他的对应边和对应角.
解:对应边:AB与AC,AE与AD,BE与CD,对应角:∠BAE与∠CAD.
【教师点拨】根据位置元素来找:有相等元素,它们就是对应元素,然后再依据已知的对应元素找出其余的对应元素.常用方法有:(1)全等三角形对应角所对的边是对应边;两个对应角所夹的边也是对应边.(2)全等三角形对应边所对的角是对应角;两条对应边所夹的角是对应角.
2.如图,△ABC≌△CDA.求证:AB∥CD.
证明:∵△ABC≌△CDA,∴∠BAC=∠DCA,∴AB∥CD.
【教师点拨】注意对应关系.
活动3 课堂小结
通过本节课学习,我们了解了全等的概念,发现了全等三角形的性质,并且利用性质可以找到两个全等三角形的对应元素.这也是这节课大家要重点掌握的.
找对应元素的常用方法有两种:
(一)从运动角度看
1.翻转法:找到中心线,沿中心线翻折后能相互重合,从而发现对应元素.
2.旋转法:三角形绕某一点旋转一定角度能与另一个三角形重合,从而发现对应元素.
3.平移法:沿某一方向平移使两三角形重合来找对应元素.
(二)根据位置元素来推理
1.全等三角形对应角所对的边是对应边;两个对应角所夹的边是对应边.
2.全等三角形对应边所对的角是对应角;两条对应边所夹的角是对应角.
【随堂训练】
教学至此,敬请使用学案随堂训练部分.
12.1 全等三角形
【出示目标】
1.知道什么是全等形、全等三角形及全等三角形的对应元素.
2.知道全等三角形的性质,能用符号正确地表示两个三角形全等
3.能熟练找出两个全等三角形的对应角、对应边.
【预习导学】
阅读教材P31-32“两个思考”,理解“全等形”、“全等三角形”的概念及其性质,学生独立完成下列问题:
【自学反馈】
(1)下列图形中的全等图形是__d__与__g__、__e__与__h__.
(2)如图,△ABC与△DEF能重合,则记作:__△ABC≌△DEF__,读作:__△ABC全等于△DEF
,对应顶点是:__A与D__、__B与E__、__C与F__;对应边是:__AB与DE__、__AC与DF__、__BC与EF__;对应角是:__∠A与∠D__、__∠B与∠E__、__∠C与∠F
.
【教师点拨】通常把对应顶点的字母写在对应的位置上.
阅读教材P32“思考”,掌握“全等三角形的性质”,并尝试应用.
【自学反馈】
(1)如图,△OCA≌△OBD,C和B,A和D是对应顶点,相等的边有__AC=DB,CO=BO,AO=DO__,相等的角有
∠A=∠D,∠C=∠B,∠COA=∠BOD
.
(2)△OCA≌△OBD,且OC=3
cm,BD=4
cm,OD=6
cm,则△OCA的周长为__13cm__.若∠C=110°,∠A=30°,则∠BOC=__140°__.
【教师点拨】全等三角形的对应边相等;全等三角形的对应角相等;全等三角形的周长相等.
【合作探究】
活动1 小组讨论
【例】如图,下面各图的两个三角形全等,指出它们的对应顶点、对应边、对应角;其中△ABC可以经过怎样的变换得到另一个三角形?
图甲 图乙 图丙
解:甲:对应顶点是点A与点D,点B与点E,点C与点F;
对应边是AB与DE,AC与DF,BC与EF;
对应角是∠A与∠D,∠B与∠E,∠C与∠F;
△ABC经过平移得到另一个三角形.
乙:对应顶点是点A与点D,点B与点B,点C与点C;
对应边是AB与DB,AC与DC,BC与BC;
对应角是∠A与∠D,∠ABC与∠DBC,∠ACB与∠DCB;
△ABC经过向下翻折得到另一个三角形.
丙:对应顶点是点D与点C,点A与点A,点E与点B;
对应边是AD与AC,AE与AB,DE与CB;
对应角是∠D与∠C,∠E与∠B,∠DAE与∠CAB;
△ABC经过旋转得到另一个三角形.
【教师点拨】一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,所以平移、翻折、旋转前后的图形全等,这也是我们通过运动的方法寻求全等的一种策略.
活动2 跟踪训练
1.如图,已知△ABE≌△ACD,∠ADE=∠AED,∠B=∠C,指出其他的对应边和对应角.
解:对应边:AB与AC,AE与AD,BE与CD,对应角:∠BAE与∠CAD.
【教师点拨】根据位置元素来找:有相等元素,它们就是对应元素,然后再依据已知的对应元素找出其余的对应元素.常用方法有:(1)全等三角形对应角所对的边是对应边;两个对应角所夹的边也是对应边.(2)全等三角形对应边所对的角是对应角;两条对应边所夹的角是对应角.
2.如图,△ABC≌△CDA.求证:AB∥CD.
证明:∵△ABC≌△CDA,∴∠BAC=∠DCA,∴AB∥CD.
【教师点拨】注意对应关系.
活动3 课堂小结
通过本节课学习,我们了解了全等的概念,发现了全等三角形的性质,并且利用性质可以找到两个全等三角形的对应元素.这也是这节课大家要重点掌握的.
找对应元素的常用方法有两种:
(一)从运动角度看
1.翻转法:找到中心线,沿中心线翻折后能相互重合,从而发现对应元素.
2.旋转法:三角形绕某一点旋转一定角度能与另一个三角形重合,从而发现对应元素.
3.平移法:沿某一方向平移使两三角形重合来找对应元素.
(二)根据位置元素来推理
1.全等三角形对应角所对的边是对应边;两个对应角所夹的边是对应边.
2.全等三角形对应边所对的角是对应角;两条对应边所夹的角是对应角.
【随堂训练】
教学至此,敬请使用学案随堂训练部分.
