人教版八年级数学上册13.2画轴对称图形 第2课时用坐标表示轴对称导学案(word版含答案)
文档属性
| 名称 | 人教版八年级数学上册13.2画轴对称图形 第2课时用坐标表示轴对称导学案(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 33.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 17:23:59 | ||
图片预览

文档简介
第十三章 轴对称
13.2 画轴对称图形
第2课时 用坐标表示轴对称
【出示目标】
1.探索关于x轴、y轴对称的每对对称点的规律.
2.利用关于x轴、y轴对称的点的坐标的规律,能作出关于x轴、y轴对称的图形.
【预习导学】
阅读教材P69-70“思考、归纳及例2”,掌握关于x轴、y轴对称的每对对称点的规律,学生独立完成下列问题:
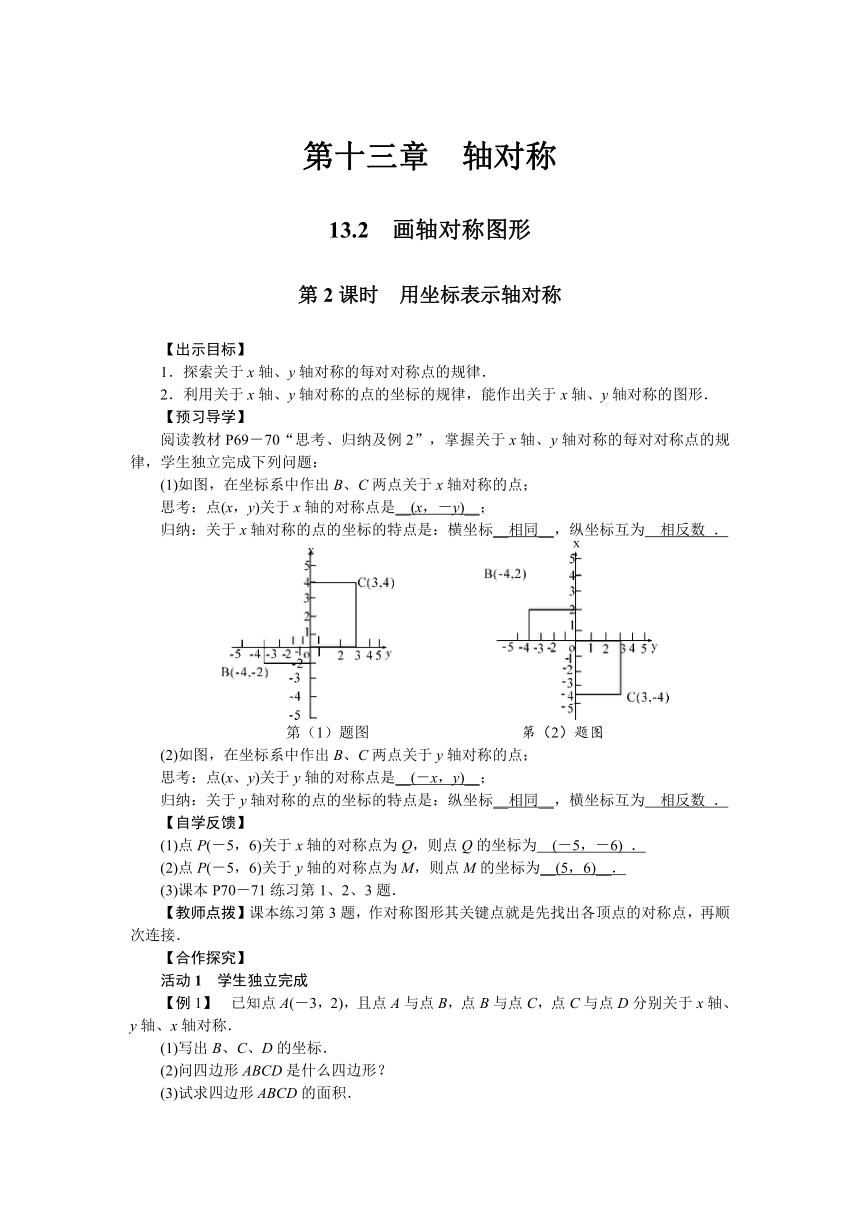
(1)如图,在坐标系中作出B、C两点关于x轴对称的点;
思考:点(x,y)关于x轴的对称点是__(x,-y)__;
归纳:关于x轴对称的点的坐标的特点是:横坐标__相同__,纵坐标互为
相反数
.
第(1)题图
第(2)题图
(2)如图,在坐标系中作出B、C两点关于y轴对称的点;
思考:点(x、y)关于y轴的对称点是__(-x,y)__;
归纳:关于y轴对称的点的坐标的特点是:纵坐标__相同__,横坐标互为
相反数
.
【自学反馈】
(1)点P(-5,6)关于x轴的对称点为Q,则点Q的坐标为
(-5,-6)
.
(2)点P(-5,6)关于y轴的对称点为M,则点M的坐标为__(5,6)__.
(3)课本P70-71练习第1、2、3题.
【教师点拨】课本练习第3题,作对称图形其关键点就是先找出各顶点的对称点,再顺次连接.
【合作探究】
活动1 学生独立完成
【例1】 已知点A(-3,2),且点A与点B,点B与点C,点C与点D分别关于x轴、y轴、x轴对称.
(1)写出B、C、D的坐标.
(2)问四边形ABCD是什么四边形?
(3)试求四边形ABCD的面积.
解:(1)点B(-3,-2),点C(3,-2),点D(3,2);
(2)四边形ABCD是矩形;
(3)S矩形ABCD=BC·AB=4×6=24.
【例2】 如图,已知△ABC的三个顶点的坐标分别是(-1,5),(-5,3),(-3,-1);作出△ABC关于x轴、y轴的对称图形.
解:如图所示,△A1B1C1和△A2B2C2即为所求作的图形.
【教师点拨】可先写出各对称点的坐标,再描点画图.
活动2 跟踪训练
1.点P(3,-4)关于x轴对称的点的坐标是( D )
A.(-4,3)
B.(-3,4)
C.(-3,-4)
D.(3,4)
2.点A(2,-3)向上平移6个单位后的点关于x轴对称的点的坐标是__(2,-3)__.
3.点P(3,4)关于y轴对称的点的坐标是P′(a,b),则a-b=__-7__.
4.若点M(a,-5)与点N(-2,b)关于x轴对称,则a=__-2__,b=__5__;若这两点关于y轴对称,则a=__2__,b=__-5__.
5.由(-1,3)→(-1,-3)经过了
x轴作轴对称变换
;由(-5,-6)→(-5,-2)经过了
向上平移4个单位长度
变换.
6.已知点P(x+1,2x-1)关于x轴对称的点在第一象限,试化简|x+2|-|1-x|.
解:2x+1.
7.如图,已知点A(4,-1),B(2,-4),C(5,-5).
(1)作出△ABC以直线y=1为对称轴的对称图形△A1B1C1;
(2)写出A、C关于直线x=-2的对称点A2、C2的坐标,及四边形ACC2A2的面积.
解:(1)略;
(2)A2(-8,-1),C2(-9,-5),S四边形ACC2A2=52.
活动3 课堂小结
解题时紧紧抓住点关于x轴、y轴和图形关于x轴、y轴对称的规律,弄清规律后就可以轻松解题了.
【随堂训练】
教学至此,敬请使用学案随堂训练部分.
13.2 画轴对称图形
第2课时 用坐标表示轴对称
【出示目标】
1.探索关于x轴、y轴对称的每对对称点的规律.
2.利用关于x轴、y轴对称的点的坐标的规律,能作出关于x轴、y轴对称的图形.
【预习导学】
阅读教材P69-70“思考、归纳及例2”,掌握关于x轴、y轴对称的每对对称点的规律,学生独立完成下列问题:
(1)如图,在坐标系中作出B、C两点关于x轴对称的点;
思考:点(x,y)关于x轴的对称点是__(x,-y)__;
归纳:关于x轴对称的点的坐标的特点是:横坐标__相同__,纵坐标互为
相反数
.
第(1)题图
第(2)题图
(2)如图,在坐标系中作出B、C两点关于y轴对称的点;
思考:点(x、y)关于y轴的对称点是__(-x,y)__;
归纳:关于y轴对称的点的坐标的特点是:纵坐标__相同__,横坐标互为
相反数
.
【自学反馈】
(1)点P(-5,6)关于x轴的对称点为Q,则点Q的坐标为
(-5,-6)
.
(2)点P(-5,6)关于y轴的对称点为M,则点M的坐标为__(5,6)__.
(3)课本P70-71练习第1、2、3题.
【教师点拨】课本练习第3题,作对称图形其关键点就是先找出各顶点的对称点,再顺次连接.
【合作探究】
活动1 学生独立完成
【例1】 已知点A(-3,2),且点A与点B,点B与点C,点C与点D分别关于x轴、y轴、x轴对称.
(1)写出B、C、D的坐标.
(2)问四边形ABCD是什么四边形?
(3)试求四边形ABCD的面积.
解:(1)点B(-3,-2),点C(3,-2),点D(3,2);
(2)四边形ABCD是矩形;
(3)S矩形ABCD=BC·AB=4×6=24.
【例2】 如图,已知△ABC的三个顶点的坐标分别是(-1,5),(-5,3),(-3,-1);作出△ABC关于x轴、y轴的对称图形.
解:如图所示,△A1B1C1和△A2B2C2即为所求作的图形.
【教师点拨】可先写出各对称点的坐标,再描点画图.
活动2 跟踪训练
1.点P(3,-4)关于x轴对称的点的坐标是( D )
A.(-4,3)
B.(-3,4)
C.(-3,-4)
D.(3,4)
2.点A(2,-3)向上平移6个单位后的点关于x轴对称的点的坐标是__(2,-3)__.
3.点P(3,4)关于y轴对称的点的坐标是P′(a,b),则a-b=__-7__.
4.若点M(a,-5)与点N(-2,b)关于x轴对称,则a=__-2__,b=__5__;若这两点关于y轴对称,则a=__2__,b=__-5__.
5.由(-1,3)→(-1,-3)经过了
x轴作轴对称变换
;由(-5,-6)→(-5,-2)经过了
向上平移4个单位长度
变换.
6.已知点P(x+1,2x-1)关于x轴对称的点在第一象限,试化简|x+2|-|1-x|.
解:2x+1.
7.如图,已知点A(4,-1),B(2,-4),C(5,-5).
(1)作出△ABC以直线y=1为对称轴的对称图形△A1B1C1;
(2)写出A、C关于直线x=-2的对称点A2、C2的坐标,及四边形ACC2A2的面积.
解:(1)略;
(2)A2(-8,-1),C2(-9,-5),S四边形ACC2A2=52.
活动3 课堂小结
解题时紧紧抓住点关于x轴、y轴和图形关于x轴、y轴对称的规律,弄清规律后就可以轻松解题了.
【随堂训练】
教学至此,敬请使用学案随堂训练部分.
