京改版数学九年级上册 18.5 相似三角形的判定(4)(29张PPT)
文档属性
| 名称 | 京改版数学九年级上册 18.5 相似三角形的判定(4)(29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 11:35:14 | ||
图片预览






文档简介
(共29张PPT)
相似三角形的判定(4)
初三年级
数学
复
习
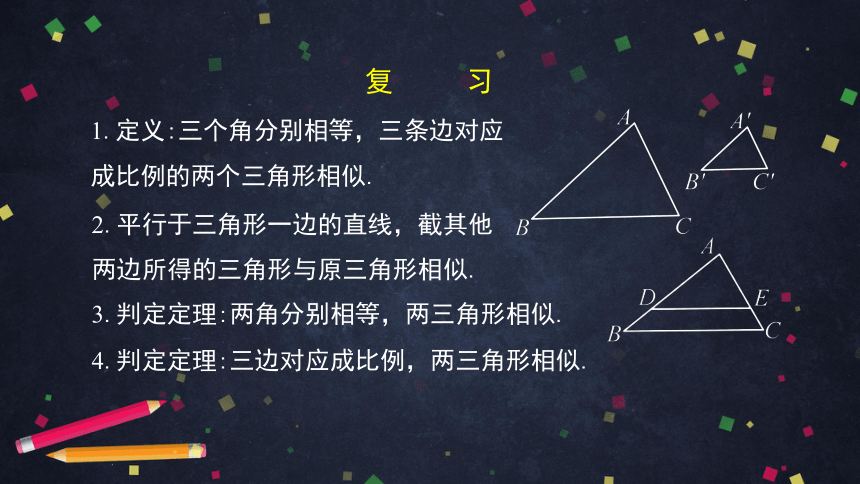
1.定义:三个角分别相等,三条边对应成比例的两个三角形相似.
3.判定定理:两角分别相等,两三角形相似.
4.判定定理:三边对应成比例,两三角形相似.
2.平行于三角形一边的直线,截其他
两边所得的三角形与原三角形相似.
判定定理的证明方法:
复
习
猜想证明
得出判定
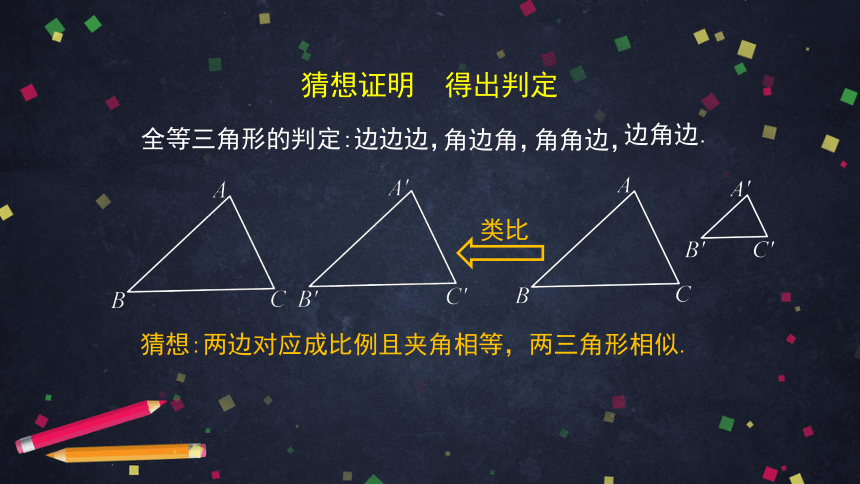
猜想:两边对应成比例且夹角相等,两三角形相似.
全等三角形的判定:边边边,
角边角,
角角边,
边角边.
类比
猜想证明
得出判定
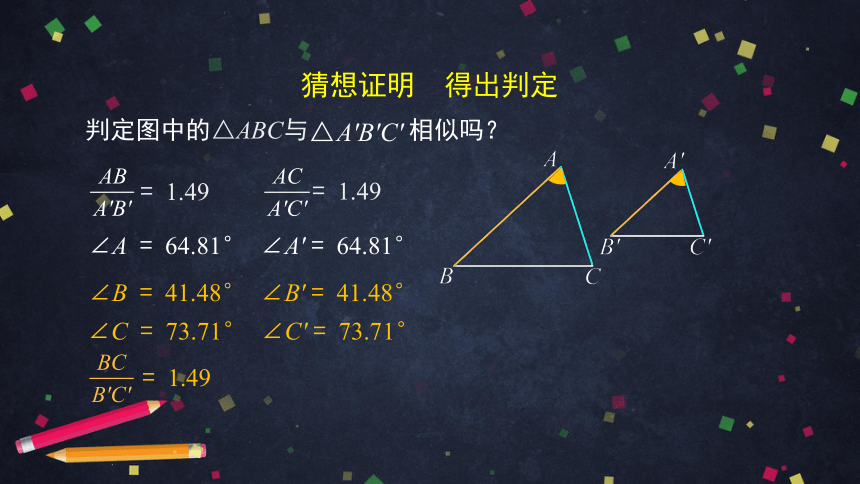
∠A
=
64.81°
∠A
=
64.81°
=
1.49
=
1.49
判定图中的△ABC与
相似吗?
∠B
=
41.48°
∠B
=
41.48°
∠C
=
73.71°
∠C
=
73.71°
=
1.49
猜想证明
得出判定
∠A
=
64.81°
∠A
=
64.81°
=
1.69
=
1.69
判定图中的△ABC与
相似吗?
∠B
=
41.48°
∠B
=
41.48°
猜想证明
得出判定
∠A
=
64.81°
∠A
=
64.81°
=
1.91
=
1.91
判定图中的△ABC与
相似吗?
∠B
=
41.48°
∠B
=
41.48°
猜想证明
得出判定
∠A
=
85.04°
∠A
=
85.04°
=
1.49
=
1.49
判定图中的△ABC与
相似吗?
∠B
=
31.66°
∠B
=
31.66°
猜想证明
得出判定
∠A
=
100.83°
∠A
=
100.83°
=
1.49
=
1.49
判定图中的△ABC与
相似吗?
∠B
=
26.17°
∠B
=
26.17°
猜想证明
得出判定
猜想:两边对应成比例且夹角相等,两三角形相似.
猜想证明
得出判定
已知:如图,在△ABC和
中,∠A
=∠A,
,
求证:△ABC
∽
.
=
猜想证明
得出判定
△ABC
∽△AKM
分析:
△ABC
∽
=
△AKM≌
已知:如图,在△ABC和
中,∠A
=∠A,
,
求证:△ABC
∽
.
=
猜想证明
得出判定
∴△ABC
∽△AKM.
∴
.
证明:在AB上截取一点K,使
,
过点K作BC的平行线交AC于点M.
=
已知:如图,在△ABC和
中,∠A
=∠A,
,
求证:△ABC
∽
.
=
猜想证明
得出判定
∵
,
且
,
∴
.
=
∴
.
已知:如图,在△ABC和
中,∠A
=∠A,
,
求证:△ABC
∽
.
=
猜想证明
得出判定
又∵
,
∴
.
△ABC
∽
∴
.
△AKM≌
已知:如图,在△ABC和
中,∠A
=∠A,
,
求证:△ABC
∽
.
=
猜想证明
得出判定
判定定理:两边对应成比例且夹角相等,两三角形相似.
在△ABC
和
中,
∵
,
=
且
,
∴
.
△ABC
∽
=
2
=
2
∠B
=
33°
∠B
=
33°
猜想证明
得出判定
小明认为:相似,并画出图形.
思考:若把判定定理中的“夹角”换成“其中一边的对角”,
两三角形还相似吗?
∠C
=
66°
∠C
=
66°
猜想证明
得出判定
思考:若把判定定理中的“夹角”换成“其中一边的对角”,
两三角形还相似吗?
以
为圆心,以
为半径画弧,
交
于D
,连接
,
应用新知
解决问题
1.依据下列条件,判定△ABC
与
是否相似,并说明理由.
∠A
=120°
AB
=7cm
,AC
=14cm;
=120°
=3cm
,
=6cm.
解:
∵
,
,
∴
.
∵∠A
=
=120°
,
∴
.
△ABC
∽
,
,
应用新知
解决问题
2.
判定图中的两个三角形是否相似,并说明理由.
∴
△ABC
∽△ABC
∵
∠ACB
=∠DCE
,
解:
∵
,
,
∴
.
∴
△ABC
∽△
.
应用新知
解决问题
例1.如图,在正方形网格上有△ABC
和△,这两个三角形相似吗?为什么?
D
E
F
A
B
C
应用新知
解决问题
例1.如图,在正方形网格上有△ABC
和△,这两个三角形相似吗?为什么?
设小正方形的边长为1,
解:
由勾股定理可得:
,
,
又∵
,
∴
.
D
E
F
A
B
C
应用新知
解决问题
例1.如图,在正方形网格上有△ABC
和△,这两个三角形相似吗?为什么?
∴△ABC
∽△DEF
.
∴
.
D
E
F
A
B
C
∵∠BAC
=∠EDF
=135°
,
应用新知
解决问题
例1.如图,在正方形网格上有△ABC
和△,这两个三角形相似吗?为什么?
设小正方形的边长为1,
由勾股定理可得:
,
解:
,
,
∴
,
,
.
D
E
F
A
B
C
应用新知
解决问题
例1.如图,在正方形网格上有△ABC
和△,这两个三角形相似吗?为什么?
∴△ABC
∽△DEF.
又∵
,
∴
.
D
E
F
A
B
C
(1)定义:三个角分别相等,三条边对应成比例的两个三角形相似.
(2)平行于三角形一边的直线,截其他两边所得的三角形与原三角形相似.
归纳小结
提升认识
(3)判定定理:两角分别相等,两三角形相似.
(4)判定定理:三边对应成比例,两三角形相似.
(5)判定定理:两边对应成比例且夹角相等,两
三角形相似.
归纳小结
提升认识
类比
边边边
角边角,
角角边
边角边
转化
归纳小结
提升认识
1.依据下列条件,判定△ABC
与
是否相似,并说明理由.
∠A
=45°,AB
=12cm
,AC
=15cm;
=45°,
=16cm
,
=20cm.
2.一个直角三角形两条直角边的长分别为6cm,4cm,另一个直角三角形两条直角边的长分别为9cm,6cm,这两个直角三角形是否相似?为什么?
课 后 作 业
相似三角形的判定(4)
初三年级
数学
复
习
1.定义:三个角分别相等,三条边对应成比例的两个三角形相似.
3.判定定理:两角分别相等,两三角形相似.
4.判定定理:三边对应成比例,两三角形相似.
2.平行于三角形一边的直线,截其他
两边所得的三角形与原三角形相似.
判定定理的证明方法:
复
习
猜想证明
得出判定
猜想:两边对应成比例且夹角相等,两三角形相似.
全等三角形的判定:边边边,
角边角,
角角边,
边角边.
类比
猜想证明
得出判定
∠A
=
64.81°
∠A
=
64.81°
=
1.49
=
1.49
判定图中的△ABC与
相似吗?
∠B
=
41.48°
∠B
=
41.48°
∠C
=
73.71°
∠C
=
73.71°
=
1.49
猜想证明
得出判定
∠A
=
64.81°
∠A
=
64.81°
=
1.69
=
1.69
判定图中的△ABC与
相似吗?
∠B
=
41.48°
∠B
=
41.48°
猜想证明
得出判定
∠A
=
64.81°
∠A
=
64.81°
=
1.91
=
1.91
判定图中的△ABC与
相似吗?
∠B
=
41.48°
∠B
=
41.48°
猜想证明
得出判定
∠A
=
85.04°
∠A
=
85.04°
=
1.49
=
1.49
判定图中的△ABC与
相似吗?
∠B
=
31.66°
∠B
=
31.66°
猜想证明
得出判定
∠A
=
100.83°
∠A
=
100.83°
=
1.49
=
1.49
判定图中的△ABC与
相似吗?
∠B
=
26.17°
∠B
=
26.17°
猜想证明
得出判定
猜想:两边对应成比例且夹角相等,两三角形相似.
猜想证明
得出判定
已知:如图,在△ABC和
中,∠A
=∠A,
,
求证:△ABC
∽
.
=
猜想证明
得出判定
△ABC
∽△AKM
分析:
△ABC
∽
=
△AKM≌
已知:如图,在△ABC和
中,∠A
=∠A,
,
求证:△ABC
∽
.
=
猜想证明
得出判定
∴△ABC
∽△AKM.
∴
.
证明:在AB上截取一点K,使
,
过点K作BC的平行线交AC于点M.
=
已知:如图,在△ABC和
中,∠A
=∠A,
,
求证:△ABC
∽
.
=
猜想证明
得出判定
∵
,
且
,
∴
.
=
∴
.
已知:如图,在△ABC和
中,∠A
=∠A,
,
求证:△ABC
∽
.
=
猜想证明
得出判定
又∵
,
∴
.
△ABC
∽
∴
.
△AKM≌
已知:如图,在△ABC和
中,∠A
=∠A,
,
求证:△ABC
∽
.
=
猜想证明
得出判定
判定定理:两边对应成比例且夹角相等,两三角形相似.
在△ABC
和
中,
∵
,
=
且
,
∴
.
△ABC
∽
=
2
=
2
∠B
=
33°
∠B
=
33°
猜想证明
得出判定
小明认为:相似,并画出图形.
思考:若把判定定理中的“夹角”换成“其中一边的对角”,
两三角形还相似吗?
∠C
=
66°
∠C
=
66°
猜想证明
得出判定
思考:若把判定定理中的“夹角”换成“其中一边的对角”,
两三角形还相似吗?
以
为圆心,以
为半径画弧,
交
于D
,连接
,
应用新知
解决问题
1.依据下列条件,判定△ABC
与
是否相似,并说明理由.
∠A
=120°
AB
=7cm
,AC
=14cm;
=120°
=3cm
,
=6cm.
解:
∵
,
,
∴
.
∵∠A
=
=120°
,
∴
.
△ABC
∽
,
,
应用新知
解决问题
2.
判定图中的两个三角形是否相似,并说明理由.
∴
△ABC
∽△ABC
∵
∠ACB
=∠DCE
,
解:
∵
,
,
∴
.
∴
△ABC
∽△
.
应用新知
解决问题
例1.如图,在正方形网格上有△ABC
和△,这两个三角形相似吗?为什么?
D
E
F
A
B
C
应用新知
解决问题
例1.如图,在正方形网格上有△ABC
和△,这两个三角形相似吗?为什么?
设小正方形的边长为1,
解:
由勾股定理可得:
,
,
又∵
,
∴
.
D
E
F
A
B
C
应用新知
解决问题
例1.如图,在正方形网格上有△ABC
和△,这两个三角形相似吗?为什么?
∴△ABC
∽△DEF
.
∴
.
D
E
F
A
B
C
∵∠BAC
=∠EDF
=135°
,
应用新知
解决问题
例1.如图,在正方形网格上有△ABC
和△,这两个三角形相似吗?为什么?
设小正方形的边长为1,
由勾股定理可得:
,
解:
,
,
∴
,
,
.
D
E
F
A
B
C
应用新知
解决问题
例1.如图,在正方形网格上有△ABC
和△,这两个三角形相似吗?为什么?
∴△ABC
∽△DEF.
又∵
,
∴
.
D
E
F
A
B
C
(1)定义:三个角分别相等,三条边对应成比例的两个三角形相似.
(2)平行于三角形一边的直线,截其他两边所得的三角形与原三角形相似.
归纳小结
提升认识
(3)判定定理:两角分别相等,两三角形相似.
(4)判定定理:三边对应成比例,两三角形相似.
(5)判定定理:两边对应成比例且夹角相等,两
三角形相似.
归纳小结
提升认识
类比
边边边
角边角,
角角边
边角边
转化
归纳小结
提升认识
1.依据下列条件,判定△ABC
与
是否相似,并说明理由.
∠A
=45°,AB
=12cm
,AC
=15cm;
=45°,
=16cm
,
=20cm.
2.一个直角三角形两条直角边的长分别为6cm,4cm,另一个直角三角形两条直角边的长分别为9cm,6cm,这两个直角三角形是否相似?为什么?
课 后 作 业
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
