京改版九年级上册数学18.2黄金分割 课件(20张PPT)
文档属性
| 名称 | 京改版九年级上册数学18.2黄金分割 课件(20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 838.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 11:36:10 | ||
图片预览




文档简介
(共20张PPT)
黄金分割
观察下列图片,它们都给人一种美与和谐的感受,你知道其中的奥秘吗?
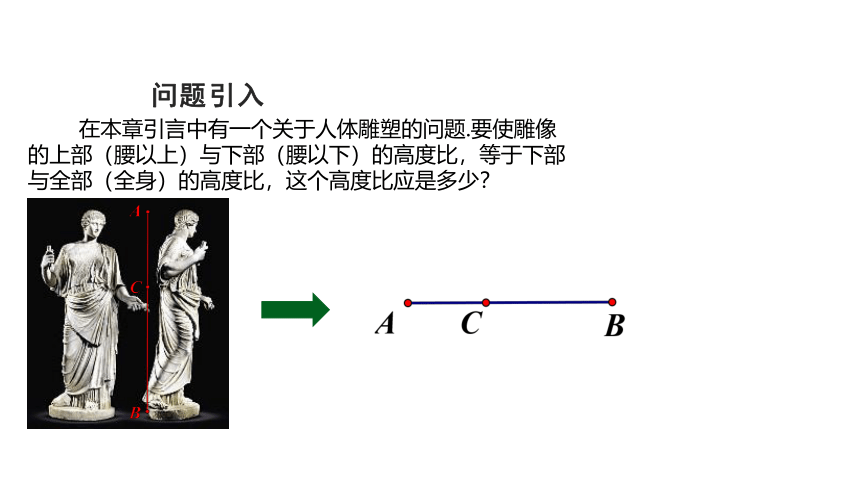
在本章引言中有一个关于人体雕塑的问题.要使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,这个高度比应是多少?
问题引入
已知:如图,点C在线段AB上,满足
.
求
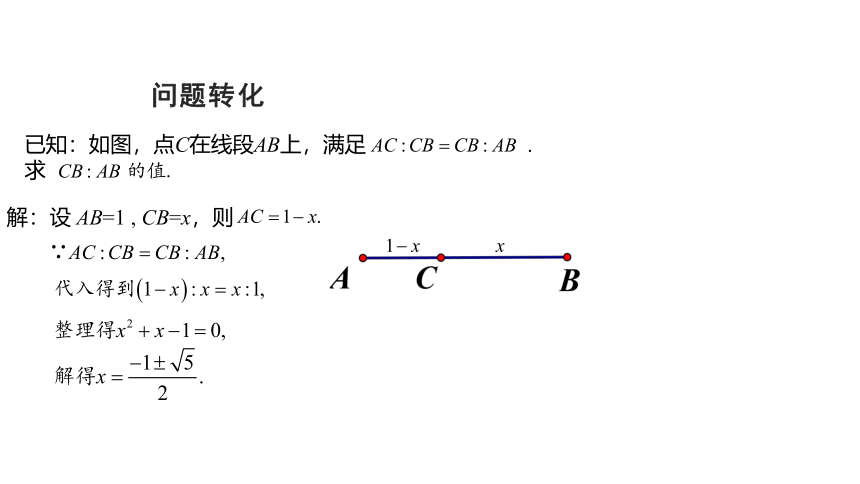
问题转化
解:设
AB=1
,
CB=x,则
已知:如图,点C在线段AB上,满足
.
求
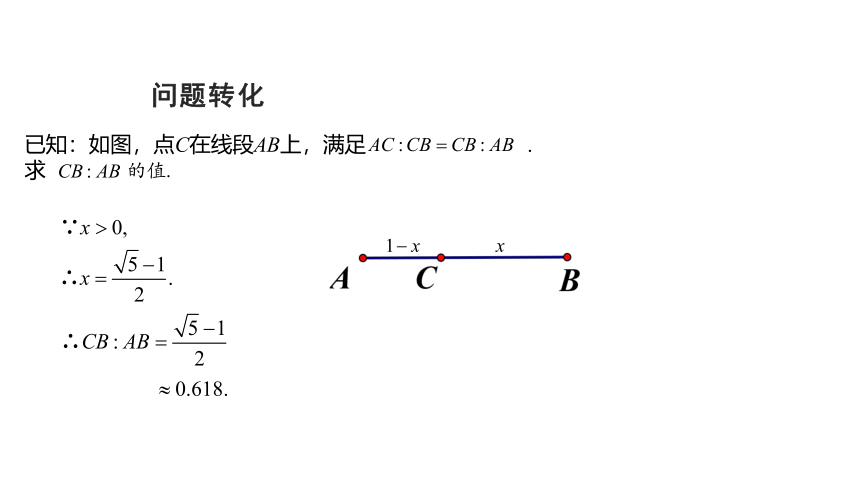
问题转化
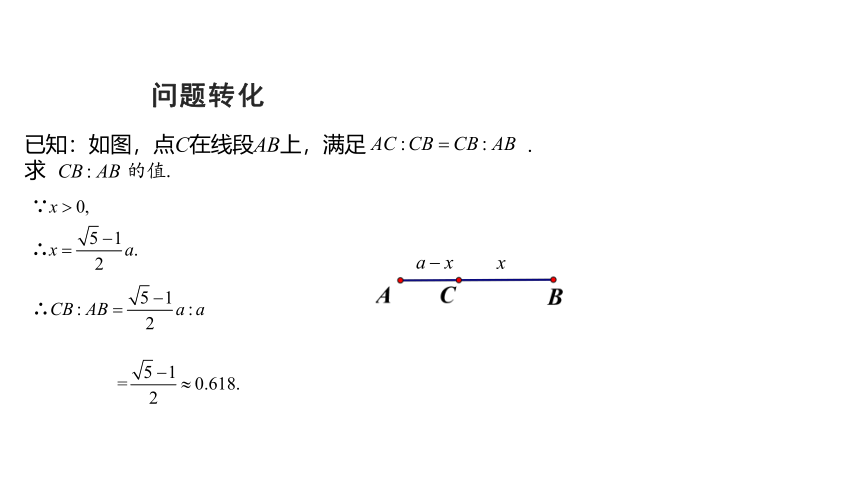
已知:如图,点C在线段AB上,满足
.
求
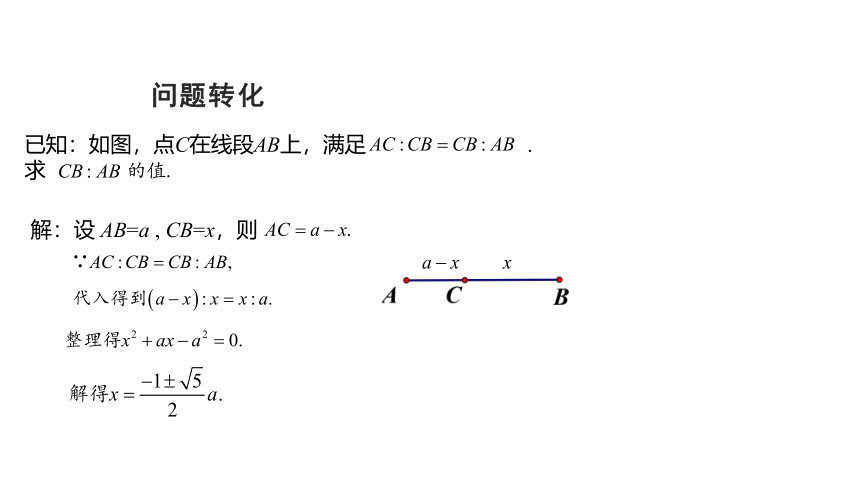
问题转化
解:设
AB=a
,
CB=x,则
已知:如图,点C在线段AB上,满足
.
求
问题转化
在本章引言中有一个关于人体雕塑的问题,要使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,这个高度比应是多少?
问题解决
根据计算,得到这个高度比为
,约为0.618.
人们把
这个数叫做黄金分割数.如果把一条线段分为两部分,使其中较长一段与整个线段的比是黄金分割数,那么较短一段与较长一段的比也是黄金分割数.
则点C为线段AB黄金分割点.
黄金分割的相关概念
一些美术家认为,如果人的上、下身长之比接近黄金分割数,那么可以增加美感.据说,一些名画和雕塑中的人体都符合这个比例.
女神维纳斯的雕像
思考:每一条线段都存在黄金分割点吗?
我们如何通过作图确定这个点的位置?
线段黄金分割点的作图
点C为线段AB的黄金分割点
分析:
线段黄金分割点的作图
a
作图步骤:
线段黄金分割点的作图
①作BD⊥AB且
②连接AD;
③在DA上截取DE=BD
;
④在AB上截取BC=AE,点C为线段AB的黄金分割点;
⑤
思考:人物站立雕像的黄金分割点是哪个?
黄金分割数的应用
N点是线段BM,BE,AP,AC的黄金分割点.
黄金分割数的应用
19米
31米
巴台农神庙侧墙东西宽31米,山墙顶部离地面19米,即东西立面高与宽之比为19:31,接近黄金分割数,让人觉得神庙非常雄伟和优雅.
黄金矩形
人们也将短边与长边之比为黄金分割数的矩形称为黄金矩形.
矩形ABCD为黄金矩形.
以AB为边在矩形内部作正方形ABFE,你能证明矩形EFCD仍为黄金矩形吗?
黄金分割数的应用
优选法是一种具有广泛应用价值的数学方法,著名数学家华罗庚曾为普及它做出重要贡献.优选法中有一种0.618法应用了黄金分割数.同学们可以查阅资料,了解0.618法的应用.
本节课小结
黄金分割数
实际问题
一元二次方程
数学建模
方程求解
同学们,再见!
黄金分割
观察下列图片,它们都给人一种美与和谐的感受,你知道其中的奥秘吗?
在本章引言中有一个关于人体雕塑的问题.要使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,这个高度比应是多少?
问题引入
已知:如图,点C在线段AB上,满足
.
求
问题转化
解:设
AB=1
,
CB=x,则
已知:如图,点C在线段AB上,满足
.
求
问题转化
已知:如图,点C在线段AB上,满足
.
求
问题转化
解:设
AB=a
,
CB=x,则
已知:如图,点C在线段AB上,满足
.
求
问题转化
在本章引言中有一个关于人体雕塑的问题,要使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,这个高度比应是多少?
问题解决
根据计算,得到这个高度比为
,约为0.618.
人们把
这个数叫做黄金分割数.如果把一条线段分为两部分,使其中较长一段与整个线段的比是黄金分割数,那么较短一段与较长一段的比也是黄金分割数.
则点C为线段AB黄金分割点.
黄金分割的相关概念
一些美术家认为,如果人的上、下身长之比接近黄金分割数,那么可以增加美感.据说,一些名画和雕塑中的人体都符合这个比例.
女神维纳斯的雕像
思考:每一条线段都存在黄金分割点吗?
我们如何通过作图确定这个点的位置?
线段黄金分割点的作图
点C为线段AB的黄金分割点
分析:
线段黄金分割点的作图
a
作图步骤:
线段黄金分割点的作图
①作BD⊥AB且
②连接AD;
③在DA上截取DE=BD
;
④在AB上截取BC=AE,点C为线段AB的黄金分割点;
⑤
思考:人物站立雕像的黄金分割点是哪个?
黄金分割数的应用
N点是线段BM,BE,AP,AC的黄金分割点.
黄金分割数的应用
19米
31米
巴台农神庙侧墙东西宽31米,山墙顶部离地面19米,即东西立面高与宽之比为19:31,接近黄金分割数,让人觉得神庙非常雄伟和优雅.
黄金矩形
人们也将短边与长边之比为黄金分割数的矩形称为黄金矩形.
矩形ABCD为黄金矩形.
以AB为边在矩形内部作正方形ABFE,你能证明矩形EFCD仍为黄金矩形吗?
黄金分割数的应用
优选法是一种具有广泛应用价值的数学方法,著名数学家华罗庚曾为普及它做出重要贡献.优选法中有一种0.618法应用了黄金分割数.同学们可以查阅资料,了解0.618法的应用.
本节课小结
黄金分割数
实际问题
一元二次方程
数学建模
方程求解
同学们,再见!
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
