京改版九年级上册 19.4 二次函数的应用(35张PPT)
文档属性
| 名称 | 京改版九年级上册 19.4 二次函数的应用(35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 11:33:16 | ||
图片预览







文档简介
(共35张PPT)
二次函数的应用(2)
初三年级
数学
y=ax2+bx+c(a≠0)
y=0
y>0
(或y<0)
ax2+bx+c=0
(a≠0)
ax2+bx+c>0
(a≠0)或
ax2+bx+c<0
(a≠0)
二次函数
一元二次不等式
一元二次方程
问题一:
求二次函数y=x2-2x-3的图象与x轴的交点A、B的坐标.
纵坐标为0
问题一:
求二次函数y=x2-2x-3的图象与x轴的交点A、B的坐标.
解:令y=0,则x2-2x-3=0
x2-2x-3=0
(x+1)(x-3)=0
问题一:
求二次函数y=x2-2x-3的图象与x轴的交点A、B的坐标.
解:令y=0,则x2-2x-3=0
解得:x1=-1,x2=3
.
∴A(-1,0),B(3,0)
.
小结
二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标就是对应的一元二次方程ax2+bx+c=0(a≠0)的两个根x1,x2
.
一元二次方程的根有三种情况:
1.有两个不相等的实数根;
2.有两个相等的实数根;
3.没有实数根.
二次函数图象与x轴的交点
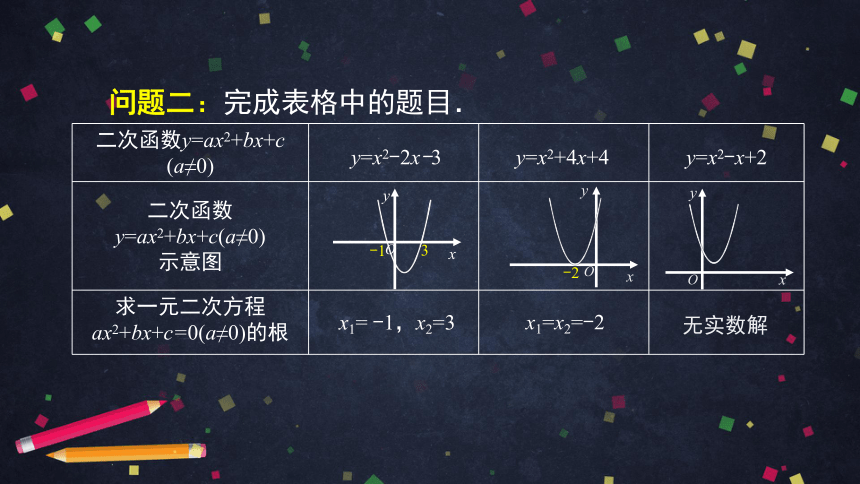
问题二:完成表格中的题目.
二次函数y=ax2+bx+c
(a≠0)
y=x2-2x-3
y=x2+4x+4
y=x2-x+2
二次函数
y=ax2+bx+c(a≠0)
示意图
求一元二次方程ax2+bx+c=0(a≠0)的根
O
y
x
-1
3
O
y
x
-2
O
y
x
x1=
-1,x2=3
x1=x2=-2
无实数解
二次函数y=ax2+bx+c
(a≠0)
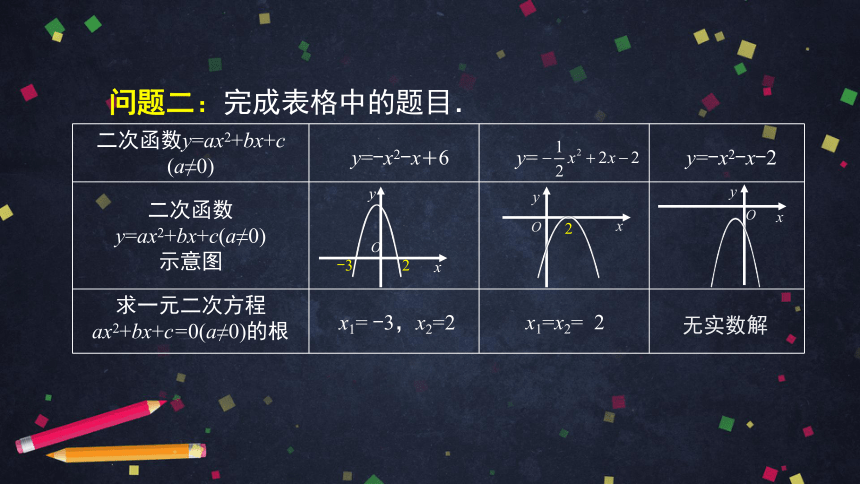
y=-x2-x+6
y=
y=-x2-x-2
二次函数
y=ax2+bx+c(a≠0)
示意图
求一元二次方程ax2+bx+c=0(a≠0)的根
O
y
x
-3
2
O
y
x
2
O
y
x
问题二:完成表格中的题目.
无实数解
x1=x2=
2
x1=
-3,x2=2
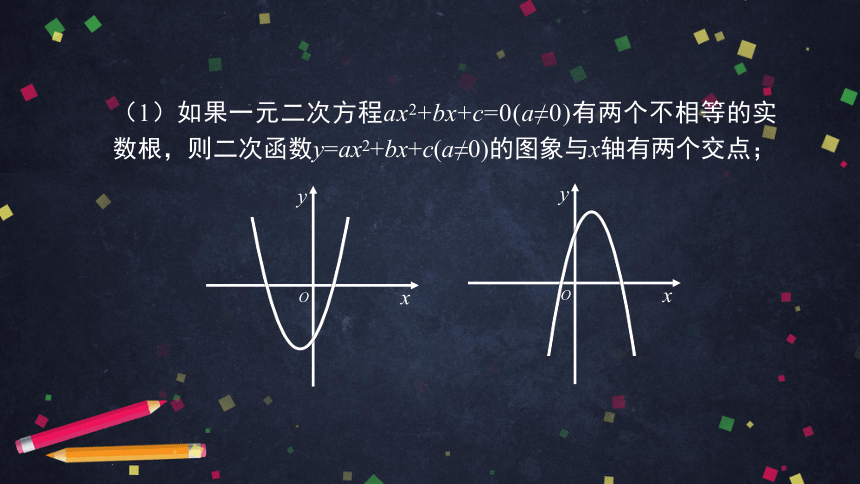
(1)如果一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实数根,则二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点;
O
y
x
O
y
x
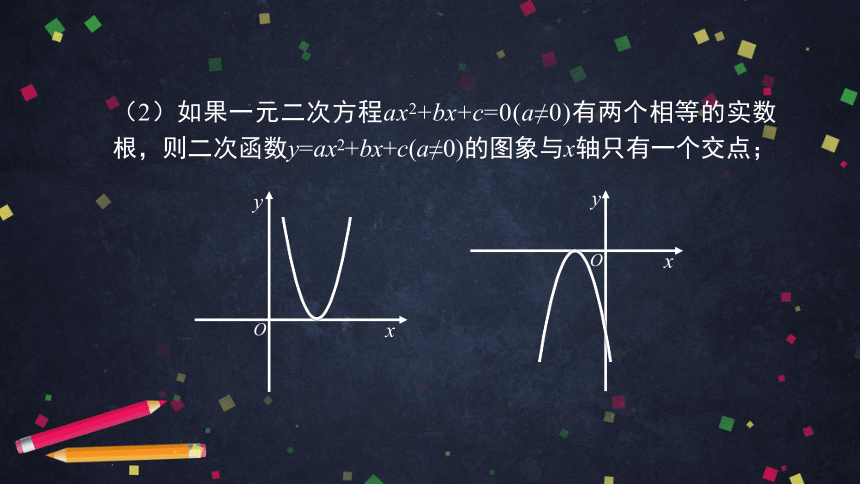
(2)如果一元二次方程ax2+bx+c=0(a≠0)有两个相等的实数根,则二次函数y=ax2+bx+c(a≠0)的图象与x轴只有一个交点;
O
y
x
O
y
x
O
y
x
O
y
x
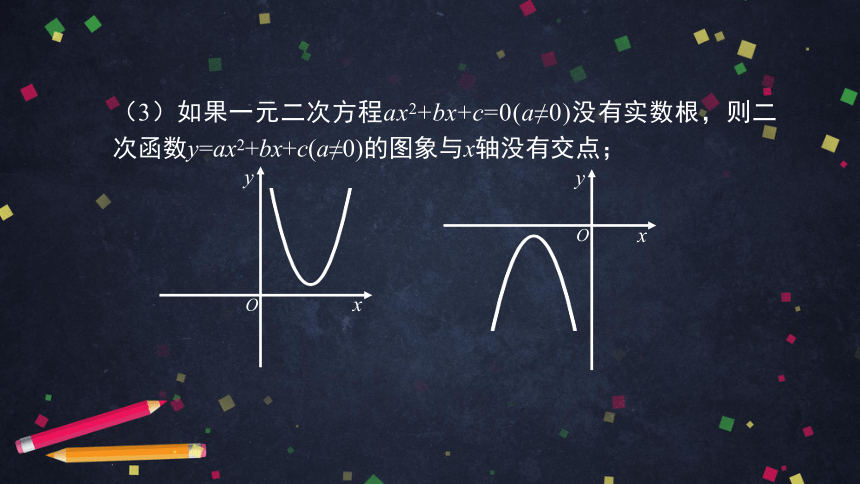
(3)如果一元二次方程ax2+bx+c=0(a≠0)没有实数根,则二次函数y=ax2+bx+c(a≠0)的图象与x轴没有交点;
ax2+bx+c=0(a≠0)
根的情况
y=ax2+bx+c(a≠0)图象与x轴的交点个数
判别式Δ=b2-4ac
一元二次方程根的情况
Δ>0
Δ=0
Δ<0
有两个不相等
实数根x1,x2
2个
有两个相等的实数根x1=x2
1个
无
无实数根
判别式
Δ=b2-4ac
例1.已知抛物线y=x2-2x+m-1与x轴最多只有一个交点,求m的取值范围.
分析:抛物线与x轴最多只有一个交点
有一个交点或没有交点
Δ
≤
0
4-4(m-1)≤
0
解:∵抛物线y=x2-2x+m-1与x轴最多只有
一个交点.
∴
Δ=b2-4ac
≤
0
.
即
4-4(m-1)≤
0
.
解得
m≥
2
.
例1.已知抛物线y=x2-2x+m-1与x轴最多只有一个交点,求m的取值范围.
二次函数
一元二次方程
根
根的判别式
图象
与x轴的交点
方程的解
小结
例2.利用函数图象求一元二次方程的近似解(精确到0.1).
解:设有二次函数
,列表并作出图象.
x
…
-1
0
1
2
3
4
5
…
y
…
-2
-4
-2
…
1
2
3
y
x
O
4
5
1
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
-0.82
0
-1
4.82
5
4
∴方程精确到0.1的近似解为
x1≈
-0.8,
x2≈
4.8
.
利用二次函数y=ax2+bx+c(a≠0)的图象求出一元二次方程ax2+bx+c
=0
(a≠0)的解的方法称为图像法.
二次函数
一元二次方程
一元二次不等式
解法?
图象
问题三:利用二次函数y=x2-2x-3的图象,你会解不等式x2-2x-3>0,x2-2x-3<0吗?
x
y
O
-1
3
x2-2x-3>0
y>0
x2-2x-3<0
y<0
x
y
O
-1
3
x=
-1
x
=
3
x<-1或x>3
-1<x
<
3
·
·
二次函数y=ax2+bx+c
(a>0)的图象
(1)图象与x轴
有2个交点;
(2)图象与x轴只
有1个交点;
(3)图象与x轴
没有交点.
O
y
x
x
O
y
O
y
x
Δ>0
Δ=0
Δ<0
x1
x2
Δ>0时
ax2+bx+c>0(a>0)
x<x1或x>x2
ax2+bx+c<0(a>0)
x1<x<x2
·
·
y
x
O
x=
x1
x=
x2
y
x
O
x1=x2
ax2+bx+c>0(a>0)
ax2+bx+c<0(a>0)
无解
x
≠
Δ=0时
=
Δ<0时
ax2+bx+c>0(a>0)
ax2+bx+c<0(a>0)
无解
全体实数
y
x
O
Δ=b2-4ac
Δ>0
Δ=0
Δ<0
y=ax2+bx+c
(a>0)的图象
ax2+bx+c>0
(a>0)的解集
ax2+bx+c<0
(a>0)的解集
y
x
O
y
x
O
y
x
O
x2
x1
x1=x2
x<x1或x>x2
x≠
全体实数
x1<
x
<
x2
无实数解
无实数解
注意:
乘以(-1)
a>0
a<0
例3.
求不等式x2-5x<0的解集
分析:(1)求一元二次方程x2-5x=0的根;
(2)画出二次函数y=x2-5x的示意图;
(3)结合方程的根及示意图求不等式的解集.
例3.
求不等式x2-5x<0的解集
解:
x2-5x
=
0.
x(x-5)
=
0.
解得:x1=0,
x2=5.
∴不等式x2-5x<0的解集为0<x<5.
x
y
O
5
x=5
总结
二次函数的图象
一元二次方程的解
一元二次不等式
(x1,0),
(x2,0)
x1,
x2
(a>0
或a<0
)
Δ=b2-4ac
总结
数形结合思想;
由特殊到一般的数学思想.
作业
1.用图象法求下列一元二次方程的近似解(精确到0.1)
(1)
(2)
作业
2.下列函数的自变量在什么范围内取值时,函数值等于零,大于零,小于零?
(1)
y
=
x2+7x-8;
(2)
y
=
-x2-x+20.
祝同学们学习进步!
再见
二次函数的应用(2)
初三年级
数学
y=ax2+bx+c(a≠0)
y=0
y>0
(或y<0)
ax2+bx+c=0
(a≠0)
ax2+bx+c>0
(a≠0)或
ax2+bx+c<0
(a≠0)
二次函数
一元二次不等式
一元二次方程
问题一:
求二次函数y=x2-2x-3的图象与x轴的交点A、B的坐标.
纵坐标为0
问题一:
求二次函数y=x2-2x-3的图象与x轴的交点A、B的坐标.
解:令y=0,则x2-2x-3=0
x2-2x-3=0
(x+1)(x-3)=0
问题一:
求二次函数y=x2-2x-3的图象与x轴的交点A、B的坐标.
解:令y=0,则x2-2x-3=0
解得:x1=-1,x2=3
.
∴A(-1,0),B(3,0)
.
小结
二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标就是对应的一元二次方程ax2+bx+c=0(a≠0)的两个根x1,x2
.
一元二次方程的根有三种情况:
1.有两个不相等的实数根;
2.有两个相等的实数根;
3.没有实数根.
二次函数图象与x轴的交点
问题二:完成表格中的题目.
二次函数y=ax2+bx+c
(a≠0)
y=x2-2x-3
y=x2+4x+4
y=x2-x+2
二次函数
y=ax2+bx+c(a≠0)
示意图
求一元二次方程ax2+bx+c=0(a≠0)的根
O
y
x
-1
3
O
y
x
-2
O
y
x
x1=
-1,x2=3
x1=x2=-2
无实数解
二次函数y=ax2+bx+c
(a≠0)
y=-x2-x+6
y=
y=-x2-x-2
二次函数
y=ax2+bx+c(a≠0)
示意图
求一元二次方程ax2+bx+c=0(a≠0)的根
O
y
x
-3
2
O
y
x
2
O
y
x
问题二:完成表格中的题目.
无实数解
x1=x2=
2
x1=
-3,x2=2
(1)如果一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实数根,则二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点;
O
y
x
O
y
x
(2)如果一元二次方程ax2+bx+c=0(a≠0)有两个相等的实数根,则二次函数y=ax2+bx+c(a≠0)的图象与x轴只有一个交点;
O
y
x
O
y
x
O
y
x
O
y
x
(3)如果一元二次方程ax2+bx+c=0(a≠0)没有实数根,则二次函数y=ax2+bx+c(a≠0)的图象与x轴没有交点;
ax2+bx+c=0(a≠0)
根的情况
y=ax2+bx+c(a≠0)图象与x轴的交点个数
判别式Δ=b2-4ac
一元二次方程根的情况
Δ>0
Δ=0
Δ<0
有两个不相等
实数根x1,x2
2个
有两个相等的实数根x1=x2
1个
无
无实数根
判别式
Δ=b2-4ac
例1.已知抛物线y=x2-2x+m-1与x轴最多只有一个交点,求m的取值范围.
分析:抛物线与x轴最多只有一个交点
有一个交点或没有交点
Δ
≤
0
4-4(m-1)≤
0
解:∵抛物线y=x2-2x+m-1与x轴最多只有
一个交点.
∴
Δ=b2-4ac
≤
0
.
即
4-4(m-1)≤
0
.
解得
m≥
2
.
例1.已知抛物线y=x2-2x+m-1与x轴最多只有一个交点,求m的取值范围.
二次函数
一元二次方程
根
根的判别式
图象
与x轴的交点
方程的解
小结
例2.利用函数图象求一元二次方程的近似解(精确到0.1).
解:设有二次函数
,列表并作出图象.
x
…
-1
0
1
2
3
4
5
…
y
…
-2
-4
-2
…
1
2
3
y
x
O
4
5
1
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
-0.82
0
-1
4.82
5
4
∴方程精确到0.1的近似解为
x1≈
-0.8,
x2≈
4.8
.
利用二次函数y=ax2+bx+c(a≠0)的图象求出一元二次方程ax2+bx+c
=0
(a≠0)的解的方法称为图像法.
二次函数
一元二次方程
一元二次不等式
解法?
图象
问题三:利用二次函数y=x2-2x-3的图象,你会解不等式x2-2x-3>0,x2-2x-3<0吗?
x
y
O
-1
3
x2-2x-3>0
y>0
x2-2x-3<0
y<0
x
y
O
-1
3
x=
-1
x
=
3
x<-1或x>3
-1<x
<
3
·
·
二次函数y=ax2+bx+c
(a>0)的图象
(1)图象与x轴
有2个交点;
(2)图象与x轴只
有1个交点;
(3)图象与x轴
没有交点.
O
y
x
x
O
y
O
y
x
Δ>0
Δ=0
Δ<0
x1
x2
Δ>0时
ax2+bx+c>0(a>0)
x<x1或x>x2
ax2+bx+c<0(a>0)
x1<x<x2
·
·
y
x
O
x=
x1
x=
x2
y
x
O
x1=x2
ax2+bx+c>0(a>0)
ax2+bx+c<0(a>0)
无解
x
≠
Δ=0时
=
Δ<0时
ax2+bx+c>0(a>0)
ax2+bx+c<0(a>0)
无解
全体实数
y
x
O
Δ=b2-4ac
Δ>0
Δ=0
Δ<0
y=ax2+bx+c
(a>0)的图象
ax2+bx+c>0
(a>0)的解集
ax2+bx+c<0
(a>0)的解集
y
x
O
y
x
O
y
x
O
x2
x1
x1=x2
x<x1或x>x2
x≠
全体实数
x1<
x
<
x2
无实数解
无实数解
注意:
乘以(-1)
a>0
a<0
例3.
求不等式x2-5x<0的解集
分析:(1)求一元二次方程x2-5x=0的根;
(2)画出二次函数y=x2-5x的示意图;
(3)结合方程的根及示意图求不等式的解集.
例3.
求不等式x2-5x<0的解集
解:
x2-5x
=
0.
x(x-5)
=
0.
解得:x1=0,
x2=5.
∴不等式x2-5x<0的解集为0<x<5.
x
y
O
5
x=5
总结
二次函数的图象
一元二次方程的解
一元二次不等式
(x1,0),
(x2,0)
x1,
x2
(a>0
或a<0
)
Δ=b2-4ac
总结
数形结合思想;
由特殊到一般的数学思想.
作业
1.用图象法求下列一元二次方程的近似解(精确到0.1)
(1)
(2)
作业
2.下列函数的自变量在什么范围内取值时,函数值等于零,大于零,小于零?
(1)
y
=
x2+7x-8;
(2)
y
=
-x2-x+20.
祝同学们学习进步!
再见
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
