12.3 角平分的性质 课件(共35张PPT)
文档属性
| 名称 | 12.3 角平分的性质 课件(共35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 13:55:12 | ||
图片预览



文档简介
(共37张PPT)
人教版
八年级上
角平分线的性质
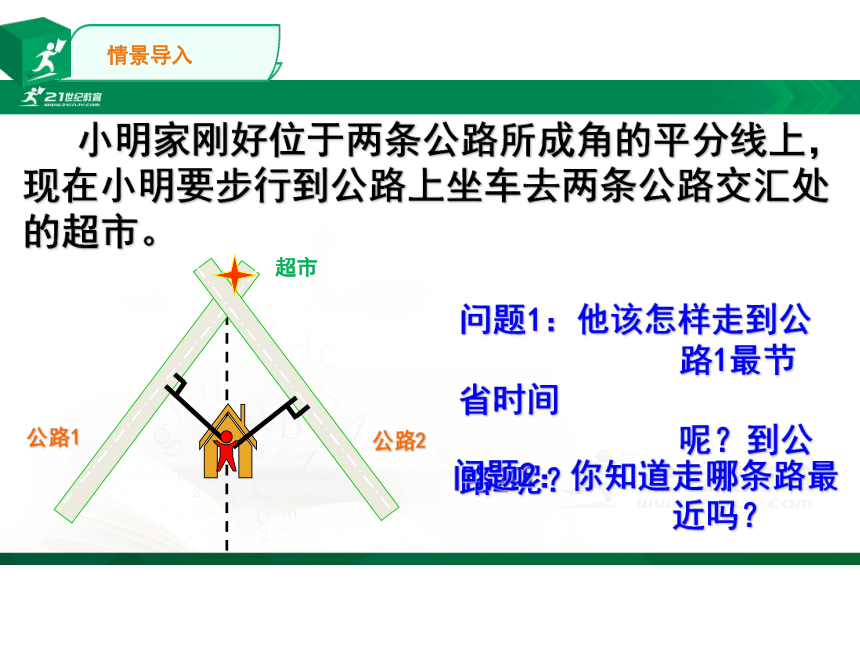
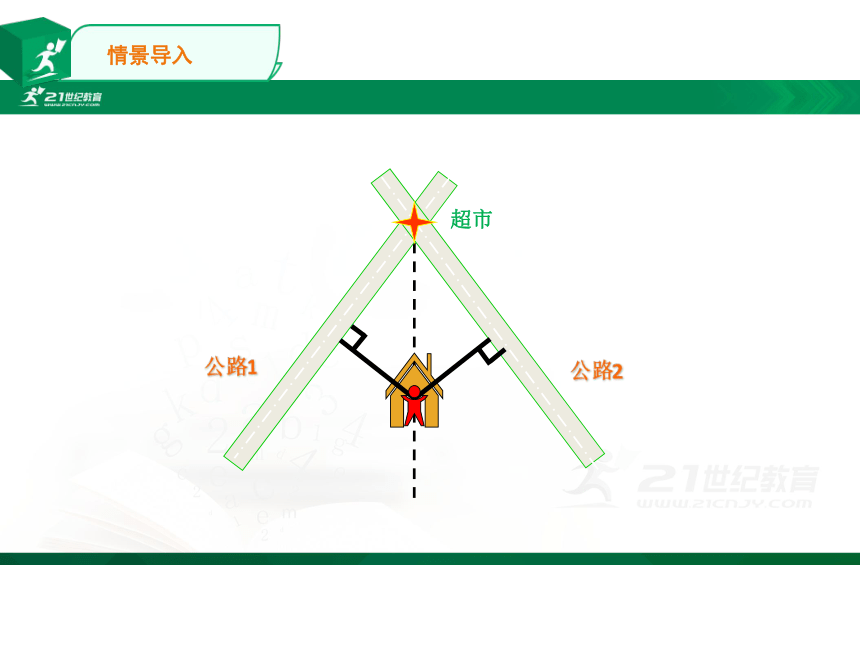
小明家刚好位于两条公路所成角的平分线上,现在小明要步行到公路上坐车去两条公路交汇处的超市。
问题1:他该怎样走到公
路1最节省时间
呢?到公路2呢?
公路2
公路1
问题2:你知道走哪条路最
近吗?
超市
情景导入
用纸剪一个角,把纸片对折,使角的两边叠合在一起,把对折后的纸片继续折一次,折出一个直三角形(使第一次的折痕为斜边),然后展开,观察两次折叠形成的三条折痕.
动手与操作
情景导入
公路2
公路1
超市
情景导入
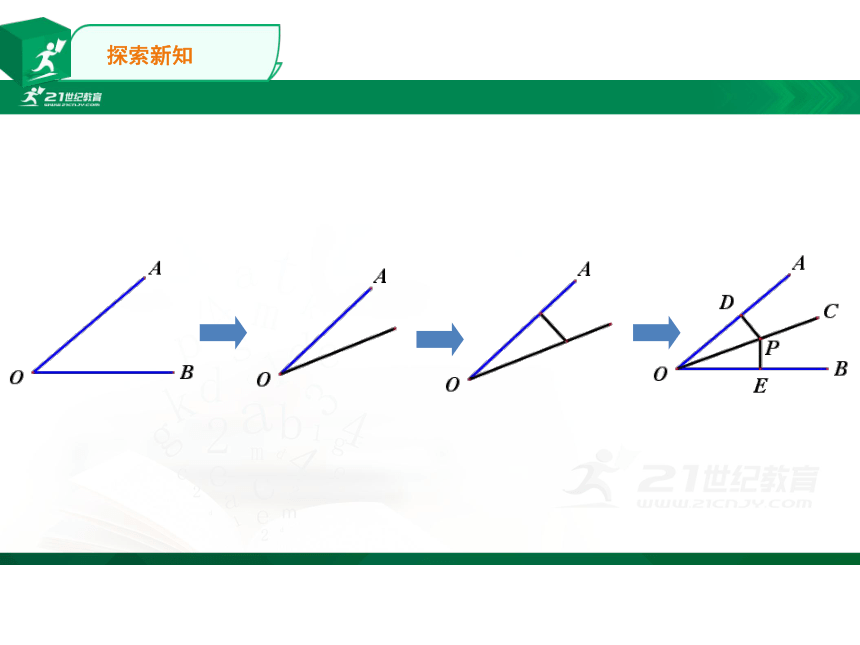
探索新知
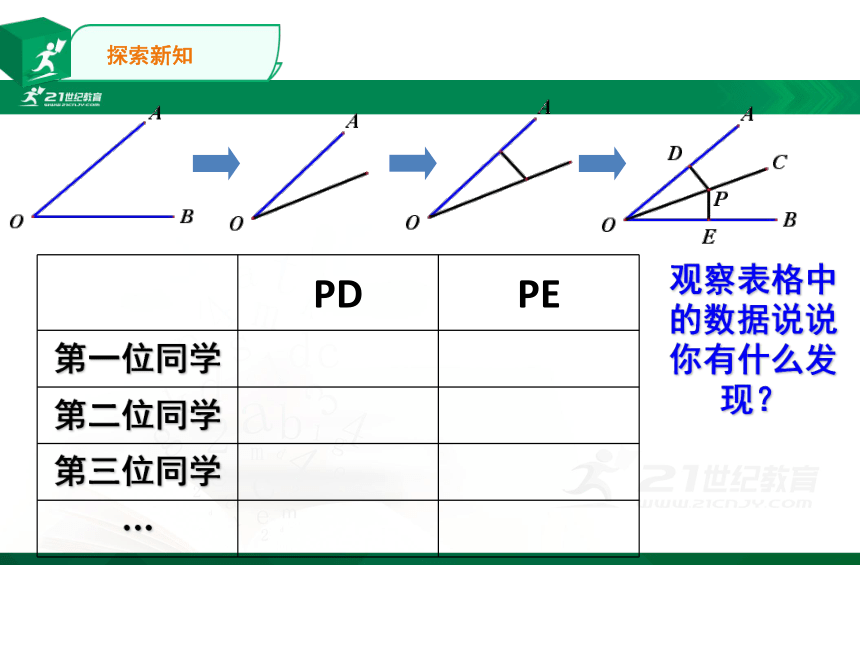
PD
PE
第一位同学
第二位同学
第三位同学
…
观察表格中的数据说说你有什么发现?
探索新知
角的平分线上的点到角的两边的距离相等。
当真如此吗?
探索新知
公路2
公路1
超市
几何模型
2
1
O
A
B
P
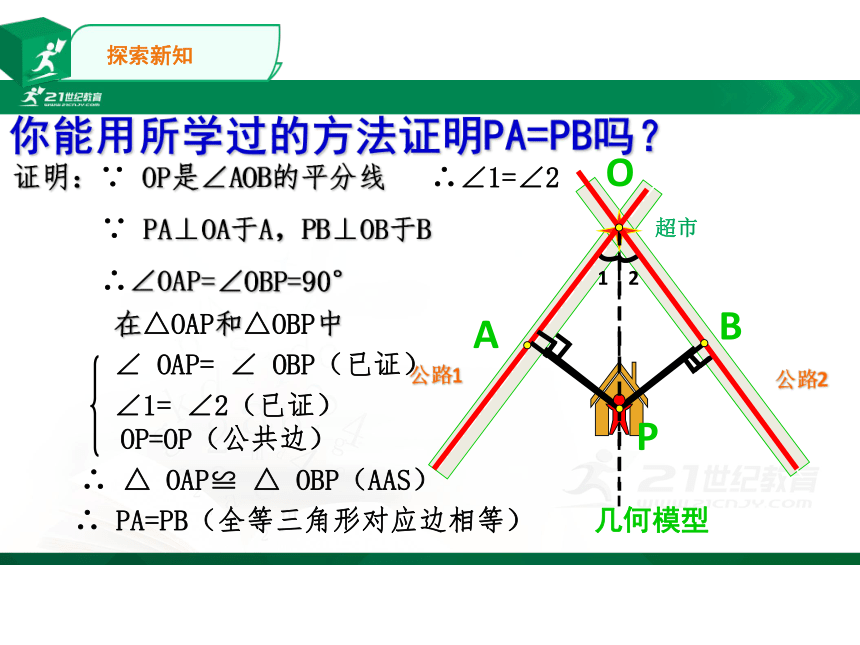
你能用所学过的方法证明PA=PB吗?
证明:∵
OP是∠AOB的平分线
∴∠1=∠2
在△OAP和△OBP中
∠1=
∠2(已证)
∴
△
OAP≌
△
OBP(AAS)
∴
PA=PB(全等三角形对应边相等)
∵
PA⊥OA于A,PB⊥OB于B
∴∠OAP=∠OBP=90°
∠
OAP=
∠
OBP(已证)
OP=OP(公共边)
探索新知
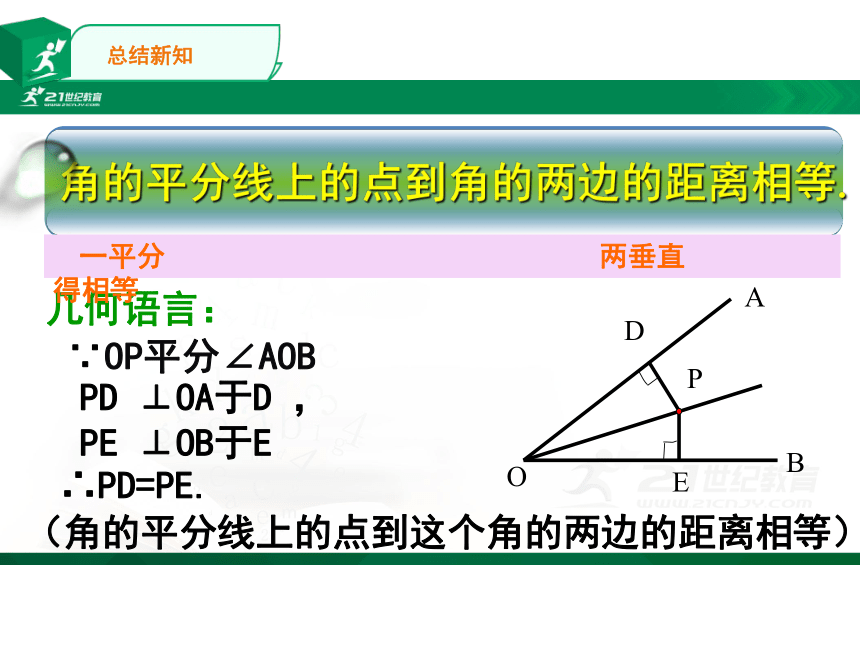
角的平分线上的点到角的两边的距离相等.
PD
⊥OA于D
,
PE
⊥OB于E
∵OP平分∠AOB
∴PD=PE.
几何语言:
一平分
两垂直
得相等
(角的平分线上的点到这个角的两边的距离相等)
A
O
B
P
E
D
总结新知
1
2
3
4
5
6
幸运5+1
6个金蛋任你选择,其中1个金蛋是直接通关,
其余5个金蛋有相应的题目,答对奖励卡片,答
错则机会属于别人,看谁是幸运的那一个!
6
游戏通关
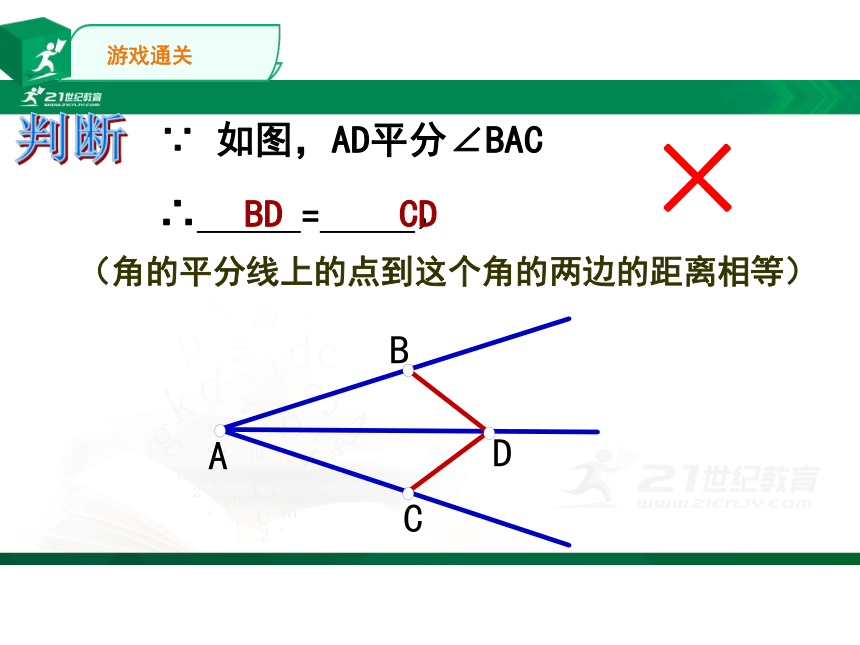
∵
如图,AD平分∠BAC
∴
=
,
(角的平分线上的点到这个角的两边的距离相等)
BD
CD
×
判断
游戏通关
1
2
3
4
5
6
幸运5+1
6个金蛋任你选择,其中1个金蛋是直接通关,
其余5个金蛋有相应的题目,答对奖励卡片,答
错则机会属于别人,看谁是幸运的那一个!
5
游戏通关
∵
如图,
DC⊥AC于C,DB⊥AB于B
∴
=
,
(角的平分线上的点到这个角的两边的距离相等)
BD
CD
×
判断
游戏通关
1
2
3
4
5
6
幸运5+1
6个金蛋任你选择,其中1个金蛋是直接通关,
其余5个金蛋有相应的题目,答对奖励卡片,答
错则机会属于别人,看谁是幸运的那一个!
4
游戏通关
恭喜你,直接通关!
游戏通过
1
2
3
4
5
6
幸运5+1
6个金蛋任你选择,其中1个金蛋是直接通关,
其余5个金蛋有相应的题目,答对奖励卡片,答
错则机会属于别人,看谁是幸运的那一个!
3
游戏通关
∵
AD平分∠BAC,DC⊥AC于C
∴
=
,
(角的平分线上的点到这个角的两边的距离相等)
BD
CD
×
判断
游戏通关
1
2
3
4
5
6
幸运5+1
6个金蛋任你选择,其中1个金蛋是直接通关,
其余5个金蛋有相应的题目,答对奖励卡片,答
错则机会属于别人,看谁是幸运的那一个!
2
游戏通关
∵
AD平分∠BAC,
DB⊥AB于B,DC⊥AC于C
∴
=
,
(角的平分线上的点到这个角的两边的距离相等)
BD
CD
√
判断
游戏通关
1
2
3
4
5
6
幸运5+1
6个金蛋任你选择,其中1个金蛋是直接通关,
其余5个金蛋有相应的题目,答对奖励卡片,答
错则机会属于别人,看谁是幸运的那一个!
1
游戏通关
如图,点D、B分别在∠EAF的两边上,C是∠EAF内一点,AB
=
AD,BC
=
DC,CE⊥AD于E,CF⊥AF于F.
求证:CE
=
CF.
游戏通关
证明:在△ABC和△ADC中
AB=AD(已知)
BC=DC
(已知)
AC=AC(公共边)
∴
△ABC≌
△ADC(SSS)
∴∠1=∠2(全等三角形对应角相等)
∴AC平分∠DAB
∵CE⊥AD于E,CF⊥AF于F
∴CE=CF(角的平分线上的点到这个角的两边的距离相等)
A
B
C
D
E
F
2
1
游戏通关
既然角平分线如此有用,我们该如何做一个角的平分线呢?
探索新知
如图,是一个角平分仪,其中AB=AD,BC=DC。
A
D
B
C
E
A
D
B
C
E
A
D
B
C
E
角平分仪的原理是什么呢?
探索新知
证明:在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
AC=AC(公共边)
∴
△ACD≌
△ACB(SSS)
∴∠CAD=∠CAB
(全等三角形对应角相等)
∴AC平分∠DAB
A
D
B
C
E
探索新知
根据角平分仪的制作原理怎样用尺规作一个角的平分线?
D
A
B
E
C
1.把角平分仪放在角的两边时,角平分仪两边AB=AD从几何作图角度怎么画?
2.BC=DC从几何作图角度怎么画?
3.射线OC与角平分仪中的AE代表
同一条射线吗?
O
A
B
C
探索新知
2.分别以点M,N为圆心.大于
MN的长为半径画弧.两弧在∠AOB的内部交于点C.
A
B
O
M
N
C
方法:
1.以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
3.作射线OC.
则射线OC即为所求.
盖理同角平分仪也!
△OMC≌△ONC(SSS)
探索新知
动手试试画出平角∠AOB的平分线。
通过上面的步骤,得射线OC以后,把它反向延长得到直线CD,直线CD与直线AB是什么关系?
B
A
O
C
D
结论
作平角的平分线即可平分平角,也是过直线上一点作这条直线的垂线的方法。
探索新知
如图∠C=
90°
,AD平分∠
CAB,DE⊥AB于点E。若
BD=2DE=6,求BC的长度。
A
B
C
D
E
课堂训练
A
B
C
D
E
解:∵∠C=
90°
∴AC⊥BC于C
又∵AD平分∠
CAB,
DE⊥AB于E
∴DC=DE
(角的平分线上的点到这个角
的两边的距离相等)
又∵BD=2DE=6
∴DC=DE=3
∴BC=BD+DC=6+3=9
课堂训练
如图,在△ABC中,∠B=90°,AC=10,AD是△ABC的一条角平分线。若BD=3,则求△ACD的面积。
A
B
D
C
E
课堂训练
A
B
D
C
E
E
解:过点D作DE⊥AC于E
∵∠B=
90°
∴AB⊥BC于B
又∵AD平分∠BAC,BD=3
∴DE=BD=3
(角的平分线上的点到这个角的两边的距离相等)
∵AC=10
∴S△ACD=
AC
DE
=
10
3
=15
×
×
×
×
1
2
1
2
课堂训练
如图,已知AP、CP分别是△ABC的外角∠DAC、∠ECA的平分线,PM⊥BD,PN⊥BE,垂足分别为M、N,那么PM与PN的数量关系是什么?
B
C
P
A
M
N
E
D
Q
课堂训练
解:过点P作PQ⊥AC于Q
∵PM⊥AD于M,
AP平分∠
DAC
∴PM=PQ
(角的平分线上的点到这
个角的两边的距离相等)
同理可证PQ=PN
∴PM=PQ=PN
即PM=PN
思考
点P在∠B的平分线上吗?
B
C
P
A
M
N
E
D
课堂训练
2、画一个已知角的角平分线
及画一条已知直线的垂线
1、角平分线的性质:
角的平分线上的点到角的两边的距离相等.
3、角平分线的应用
谈谈这节课你有什么收获?
课堂小结
https://www.21cnjy.com/help/help_extract.php
人教版
八年级上
角平分线的性质
小明家刚好位于两条公路所成角的平分线上,现在小明要步行到公路上坐车去两条公路交汇处的超市。
问题1:他该怎样走到公
路1最节省时间
呢?到公路2呢?
公路2
公路1
问题2:你知道走哪条路最
近吗?
超市
情景导入
用纸剪一个角,把纸片对折,使角的两边叠合在一起,把对折后的纸片继续折一次,折出一个直三角形(使第一次的折痕为斜边),然后展开,观察两次折叠形成的三条折痕.
动手与操作
情景导入
公路2
公路1
超市
情景导入
探索新知
PD
PE
第一位同学
第二位同学
第三位同学
…
观察表格中的数据说说你有什么发现?
探索新知
角的平分线上的点到角的两边的距离相等。
当真如此吗?
探索新知
公路2
公路1
超市
几何模型
2
1
O
A
B
P
你能用所学过的方法证明PA=PB吗?
证明:∵
OP是∠AOB的平分线
∴∠1=∠2
在△OAP和△OBP中
∠1=
∠2(已证)
∴
△
OAP≌
△
OBP(AAS)
∴
PA=PB(全等三角形对应边相等)
∵
PA⊥OA于A,PB⊥OB于B
∴∠OAP=∠OBP=90°
∠
OAP=
∠
OBP(已证)
OP=OP(公共边)
探索新知
角的平分线上的点到角的两边的距离相等.
PD
⊥OA于D
,
PE
⊥OB于E
∵OP平分∠AOB
∴PD=PE.
几何语言:
一平分
两垂直
得相等
(角的平分线上的点到这个角的两边的距离相等)
A
O
B
P
E
D
总结新知
1
2
3
4
5
6
幸运5+1
6个金蛋任你选择,其中1个金蛋是直接通关,
其余5个金蛋有相应的题目,答对奖励卡片,答
错则机会属于别人,看谁是幸运的那一个!
6
游戏通关
∵
如图,AD平分∠BAC
∴
=
,
(角的平分线上的点到这个角的两边的距离相等)
BD
CD
×
判断
游戏通关
1
2
3
4
5
6
幸运5+1
6个金蛋任你选择,其中1个金蛋是直接通关,
其余5个金蛋有相应的题目,答对奖励卡片,答
错则机会属于别人,看谁是幸运的那一个!
5
游戏通关
∵
如图,
DC⊥AC于C,DB⊥AB于B
∴
=
,
(角的平分线上的点到这个角的两边的距离相等)
BD
CD
×
判断
游戏通关
1
2
3
4
5
6
幸运5+1
6个金蛋任你选择,其中1个金蛋是直接通关,
其余5个金蛋有相应的题目,答对奖励卡片,答
错则机会属于别人,看谁是幸运的那一个!
4
游戏通关
恭喜你,直接通关!
游戏通过
1
2
3
4
5
6
幸运5+1
6个金蛋任你选择,其中1个金蛋是直接通关,
其余5个金蛋有相应的题目,答对奖励卡片,答
错则机会属于别人,看谁是幸运的那一个!
3
游戏通关
∵
AD平分∠BAC,DC⊥AC于C
∴
=
,
(角的平分线上的点到这个角的两边的距离相等)
BD
CD
×
判断
游戏通关
1
2
3
4
5
6
幸运5+1
6个金蛋任你选择,其中1个金蛋是直接通关,
其余5个金蛋有相应的题目,答对奖励卡片,答
错则机会属于别人,看谁是幸运的那一个!
2
游戏通关
∵
AD平分∠BAC,
DB⊥AB于B,DC⊥AC于C
∴
=
,
(角的平分线上的点到这个角的两边的距离相等)
BD
CD
√
判断
游戏通关
1
2
3
4
5
6
幸运5+1
6个金蛋任你选择,其中1个金蛋是直接通关,
其余5个金蛋有相应的题目,答对奖励卡片,答
错则机会属于别人,看谁是幸运的那一个!
1
游戏通关
如图,点D、B分别在∠EAF的两边上,C是∠EAF内一点,AB
=
AD,BC
=
DC,CE⊥AD于E,CF⊥AF于F.
求证:CE
=
CF.
游戏通关
证明:在△ABC和△ADC中
AB=AD(已知)
BC=DC
(已知)
AC=AC(公共边)
∴
△ABC≌
△ADC(SSS)
∴∠1=∠2(全等三角形对应角相等)
∴AC平分∠DAB
∵CE⊥AD于E,CF⊥AF于F
∴CE=CF(角的平分线上的点到这个角的两边的距离相等)
A
B
C
D
E
F
2
1
游戏通关
既然角平分线如此有用,我们该如何做一个角的平分线呢?
探索新知
如图,是一个角平分仪,其中AB=AD,BC=DC。
A
D
B
C
E
A
D
B
C
E
A
D
B
C
E
角平分仪的原理是什么呢?
探索新知
证明:在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
AC=AC(公共边)
∴
△ACD≌
△ACB(SSS)
∴∠CAD=∠CAB
(全等三角形对应角相等)
∴AC平分∠DAB
A
D
B
C
E
探索新知
根据角平分仪的制作原理怎样用尺规作一个角的平分线?
D
A
B
E
C
1.把角平分仪放在角的两边时,角平分仪两边AB=AD从几何作图角度怎么画?
2.BC=DC从几何作图角度怎么画?
3.射线OC与角平分仪中的AE代表
同一条射线吗?
O
A
B
C
探索新知
2.分别以点M,N为圆心.大于
MN的长为半径画弧.两弧在∠AOB的内部交于点C.
A
B
O
M
N
C
方法:
1.以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
3.作射线OC.
则射线OC即为所求.
盖理同角平分仪也!
△OMC≌△ONC(SSS)
探索新知
动手试试画出平角∠AOB的平分线。
通过上面的步骤,得射线OC以后,把它反向延长得到直线CD,直线CD与直线AB是什么关系?
B
A
O
C
D
结论
作平角的平分线即可平分平角,也是过直线上一点作这条直线的垂线的方法。
探索新知
如图∠C=
90°
,AD平分∠
CAB,DE⊥AB于点E。若
BD=2DE=6,求BC的长度。
A
B
C
D
E
课堂训练
A
B
C
D
E
解:∵∠C=
90°
∴AC⊥BC于C
又∵AD平分∠
CAB,
DE⊥AB于E
∴DC=DE
(角的平分线上的点到这个角
的两边的距离相等)
又∵BD=2DE=6
∴DC=DE=3
∴BC=BD+DC=6+3=9
课堂训练
如图,在△ABC中,∠B=90°,AC=10,AD是△ABC的一条角平分线。若BD=3,则求△ACD的面积。
A
B
D
C
E
课堂训练
A
B
D
C
E
E
解:过点D作DE⊥AC于E
∵∠B=
90°
∴AB⊥BC于B
又∵AD平分∠BAC,BD=3
∴DE=BD=3
(角的平分线上的点到这个角的两边的距离相等)
∵AC=10
∴S△ACD=
AC
DE
=
10
3
=15
×
×
×
×
1
2
1
2
课堂训练
如图,已知AP、CP分别是△ABC的外角∠DAC、∠ECA的平分线,PM⊥BD,PN⊥BE,垂足分别为M、N,那么PM与PN的数量关系是什么?
B
C
P
A
M
N
E
D
Q
课堂训练
解:过点P作PQ⊥AC于Q
∵PM⊥AD于M,
AP平分∠
DAC
∴PM=PQ
(角的平分线上的点到这
个角的两边的距离相等)
同理可证PQ=PN
∴PM=PQ=PN
即PM=PN
思考
点P在∠B的平分线上吗?
B
C
P
A
M
N
E
D
课堂训练
2、画一个已知角的角平分线
及画一条已知直线的垂线
1、角平分线的性质:
角的平分线上的点到角的两边的距离相等.
3、角平分线的应用
谈谈这节课你有什么收获?
课堂小结
https://www.21cnjy.com/help/help_extract.php
