12.4《全等三角形》课时练习2021-2022学年北京课改版数学八年级上册(word版含答案)
文档属性
| 名称 | 12.4《全等三角形》课时练习2021-2022学年北京课改版数学八年级上册(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 117.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 00:00:00 | ||
图片预览

文档简介
北京课改版数学八年级上册
12.4《全等三角形》课时练习
一、选择题
1.如果△ABC与△DEF是全等形,则有( )
(1)它们的周长相等;
(2)它们的面积相等;
(3)它们的每个对应角都相等;
(4)它们的每条对应边都相等.
A.(1)(2)(3)(4)
B.(1)(2)(3)
C.(1)(2)
D.(1)
2.下列叙述中错误的是( )
A.能够重合的图形称为全等图形
B.全等图形的形状和大小都相同
C.所有正方形都是全等图形
D.形状和大小都相同的两个图形是全等图形
3.下列命题中:
(1)形状相同的两个三角形是全等形;
(2)在两个全等三角形中,相等的角是对应角,相等的边是对应边;
(3)全等三角形对应边上的高、中线及对应角平分线分别相等.
其中真命题的个数有(
)
A.3个
B.2个
C.1个
D.0个
4.若△ABC≌△DEF,点A和点D,点B和点E是对应点。如果AB=7cm,BC=6cm,AC=5cm,则EF的长为(??
)????????
A.4cm?????
B.5
cm????
C.6
cm???
D.7
cm
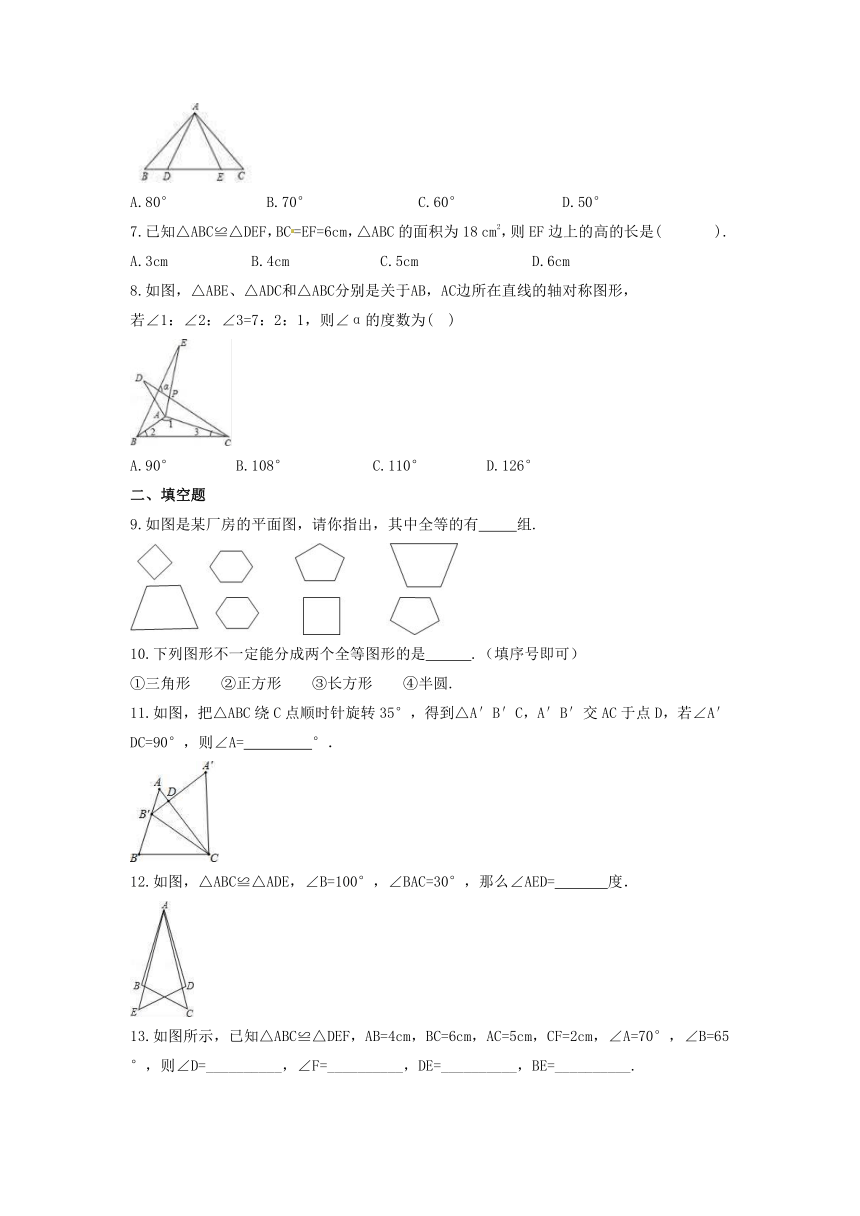
5.如图所示,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,下列不正确的等式是( )
A.AB=AC??
??
B.∠BAE=∠CAD???
??
C.BE=DC?
?
?
D.AD=DE
6.如图已知△ABE≌△ACD,
AB=AC,
BE=CD,∠B=40°,∠AEC=120°则∠DAC的度数为
( )
A.80°????
B.70°????
C.60°??
?
D.50°
7.已知△ABC≌△DEF,BC=EF=6cm,△ABC的面积为18
cm2,则EF边上的高的长是(
).
A.3cm
???
?B.4cm
?
C.5cm
???
??D.6cm
8.如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,
若∠1:∠2:∠3=7:2:1,则∠α的度数为(
)
A.90°
B.108°
C.110°
D.126°
二、填空题
9.如图是某厂房的平面图,请你指出,其中全等的有
组.
10.下列图形不一定能分成两个全等图形的是
.(填序号即可)
①三角形
②正方形
③长方形
④半圆.
11.如图,把△ABC绕C点顺时针旋转35°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A=
°.
12.如图,△ABC≌△ADE,∠B=100°,∠BAC=30°,那么∠AED=
度.
13.如图所示,已知△ABC≌△DEF,AB=4cm,BC=6cm,AC=5cm,CF=2cm,∠A=70°,∠B=65°,则∠D=__________,∠F=__________,DE=__________,BE=__________.
14.ΔABE≌ΔACD,AB=8cm,AD=5cm,∠A=60°,∠B=40°,则AE=______cm
,∠D=_______°
三、作图题
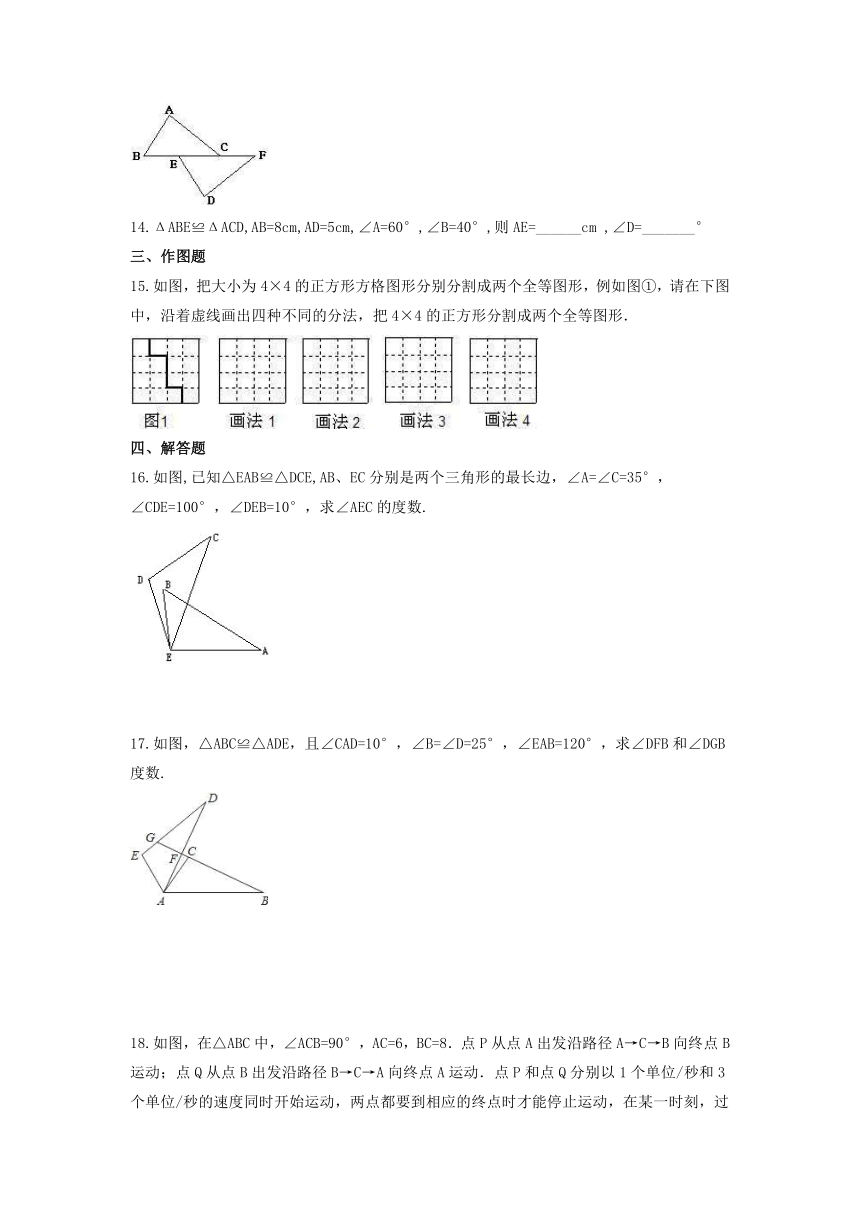
15.如图,把大小为4×4的正方形方格图形分别分割成两个全等图形,例如图①,请在下图中,沿着虚线画出四种不同的分法,把4×4的正方形分割成两个全等图形.
四、解答题
16.如图,已知△EAB≌△DCE,AB、EC分别是两个三角形的最长边,∠A=∠C=35°,
∠CDE=100°,∠DEB=10°,求∠AEC的度数.
17.如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB度数.
18.如图,在△ABC中,∠ACB=90°,AC=6,BC=8.点P从点A出发沿路径A→C→B向终点B运动;点Q从点B出发沿路径B→C→A向终点A运动.点P和点Q分别以1个单位/秒和3个单位/秒的速度同时开始运动,两点都要到相应的终点时才能停止运动,在某一时刻,过点P作PE⊥l于点E,过点Q作QF⊥l于点F.问:点P运动多少时间时,△PEC与△CFQ全等?请说明理由.
参考答案
1.A.
2.C
3.C
4.C
5.D
6.A
7.D?
8.B
9.答案为:3.
10.答案为:①.
11.答案为:55°.
12.答案为:∠AED=50度.
13.答案为:70°
45°
4cm?
2cm
14.答案为:5,80°
15.解:如图所示:
16.解:因为AB、EC是对应边,
所以∠AEB=∠CDE=100°,
又因为∠C=35°,
所以∠CED=180°-35°-100°=45°,
又因为∠DEB=10°,
所以∠BEC=45°-10°=35°,
所以∠AEC=∠AEB-∠BEC=100°-35°=65°.
17.解:∵△ABC≌△ADE,
∴∠DAE=∠BAC=(∠EAB﹣∠CAD)=.
∴∠DFB=∠FAB+∠B=∠FAC+∠CAB+∠B=10°+55°+25°=90°
∠DGB=∠DFB﹣∠D=90°﹣25°=65°.
综上所述:∠DFB=90°,∠DGB=65°.
18.解:设运动时间为t(s)时,△PEC与△CFQ全等.
∵△PEC与△CFQ全等,∴斜边CP=QC.
当0当6≤t≤14时,点P在BC上.
当0<t<时,点Q在BC上;
当≤t≤时,点Q在AC上.
有三种情况:①当点P在AC上,点Q在BC上时(0易得CP=6-t,QC=8-3t,
∴6-t=8-3t,解得t=1.
②当点P,Q都在AC上时(≤,此时点P,Q重合,如解图②.
易得CP=6-t=3t-8,解得t=3.5.
③当点Q与点A重合,点P在BC上时(6<t≤14),如解图③.
易得CP=t-6,QC=6,∴t-6=6,解得t=12.
综上所述,当点P运动1
s或3.5
s或12s时,△PEC与△CFQ全等.
12.4《全等三角形》课时练习
一、选择题
1.如果△ABC与△DEF是全等形,则有( )
(1)它们的周长相等;
(2)它们的面积相等;
(3)它们的每个对应角都相等;
(4)它们的每条对应边都相等.
A.(1)(2)(3)(4)
B.(1)(2)(3)
C.(1)(2)
D.(1)
2.下列叙述中错误的是( )
A.能够重合的图形称为全等图形
B.全等图形的形状和大小都相同
C.所有正方形都是全等图形
D.形状和大小都相同的两个图形是全等图形
3.下列命题中:
(1)形状相同的两个三角形是全等形;
(2)在两个全等三角形中,相等的角是对应角,相等的边是对应边;
(3)全等三角形对应边上的高、中线及对应角平分线分别相等.
其中真命题的个数有(
)
A.3个
B.2个
C.1个
D.0个
4.若△ABC≌△DEF,点A和点D,点B和点E是对应点。如果AB=7cm,BC=6cm,AC=5cm,则EF的长为(??
)????????
A.4cm?????
B.5
cm????
C.6
cm???
D.7
cm
5.如图所示,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,下列不正确的等式是( )
A.AB=AC??
??
B.∠BAE=∠CAD???
??
C.BE=DC?
?
?
D.AD=DE
6.如图已知△ABE≌△ACD,
AB=AC,
BE=CD,∠B=40°,∠AEC=120°则∠DAC的度数为
( )
A.80°????
B.70°????
C.60°??
?
D.50°
7.已知△ABC≌△DEF,BC=EF=6cm,△ABC的面积为18
cm2,则EF边上的高的长是(
).
A.3cm
???
?B.4cm
?
C.5cm
???
??D.6cm
8.如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,
若∠1:∠2:∠3=7:2:1,则∠α的度数为(
)
A.90°
B.108°
C.110°
D.126°
二、填空题
9.如图是某厂房的平面图,请你指出,其中全等的有
组.
10.下列图形不一定能分成两个全等图形的是
.(填序号即可)
①三角形
②正方形
③长方形
④半圆.
11.如图,把△ABC绕C点顺时针旋转35°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A=
°.
12.如图,△ABC≌△ADE,∠B=100°,∠BAC=30°,那么∠AED=
度.
13.如图所示,已知△ABC≌△DEF,AB=4cm,BC=6cm,AC=5cm,CF=2cm,∠A=70°,∠B=65°,则∠D=__________,∠F=__________,DE=__________,BE=__________.
14.ΔABE≌ΔACD,AB=8cm,AD=5cm,∠A=60°,∠B=40°,则AE=______cm
,∠D=_______°
三、作图题
15.如图,把大小为4×4的正方形方格图形分别分割成两个全等图形,例如图①,请在下图中,沿着虚线画出四种不同的分法,把4×4的正方形分割成两个全等图形.
四、解答题
16.如图,已知△EAB≌△DCE,AB、EC分别是两个三角形的最长边,∠A=∠C=35°,
∠CDE=100°,∠DEB=10°,求∠AEC的度数.
17.如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB度数.
18.如图,在△ABC中,∠ACB=90°,AC=6,BC=8.点P从点A出发沿路径A→C→B向终点B运动;点Q从点B出发沿路径B→C→A向终点A运动.点P和点Q分别以1个单位/秒和3个单位/秒的速度同时开始运动,两点都要到相应的终点时才能停止运动,在某一时刻,过点P作PE⊥l于点E,过点Q作QF⊥l于点F.问:点P运动多少时间时,△PEC与△CFQ全等?请说明理由.
参考答案
1.A.
2.C
3.C
4.C
5.D
6.A
7.D?
8.B
9.答案为:3.
10.答案为:①.
11.答案为:55°.
12.答案为:∠AED=50度.
13.答案为:70°
45°
4cm?
2cm
14.答案为:5,80°
15.解:如图所示:
16.解:因为AB、EC是对应边,
所以∠AEB=∠CDE=100°,
又因为∠C=35°,
所以∠CED=180°-35°-100°=45°,
又因为∠DEB=10°,
所以∠BEC=45°-10°=35°,
所以∠AEC=∠AEB-∠BEC=100°-35°=65°.
17.解:∵△ABC≌△ADE,
∴∠DAE=∠BAC=(∠EAB﹣∠CAD)=.
∴∠DFB=∠FAB+∠B=∠FAC+∠CAB+∠B=10°+55°+25°=90°
∠DGB=∠DFB﹣∠D=90°﹣25°=65°.
综上所述:∠DFB=90°,∠DGB=65°.
18.解:设运动时间为t(s)时,△PEC与△CFQ全等.
∵△PEC与△CFQ全等,∴斜边CP=QC.
当0
当0<t<时,点Q在BC上;
当≤t≤时,点Q在AC上.
有三种情况:①当点P在AC上,点Q在BC上时(0
∴6-t=8-3t,解得t=1.
②当点P,Q都在AC上时(≤,此时点P,Q重合,如解图②.
易得CP=6-t=3t-8,解得t=3.5.
③当点Q与点A重合,点P在BC上时(6<t≤14),如解图③.
易得CP=t-6,QC=6,∴t-6=6,解得t=12.
综上所述,当点P运动1
s或3.5
s或12s时,△PEC与△CFQ全等.
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
