2021-2022学年北京课改版数学八年级上册 12.2 三角形的性质 课时练习 (word版含答案)
文档属性
| 名称 | 2021-2022学年北京课改版数学八年级上册 12.2 三角形的性质 课时练习 (word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 91.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 20:38:33 | ||
图片预览

文档简介
北京课改版数学八年级上册
12.2《三角形的性质》课时练习
一、选择题
1.如图,在△ABC中,点D在AB上,点E在AC上,DE∥BC.若∠A=62°,∠AED=54°,
则∠B的度数为(
)
A.54°
B.62°
C.64°
D.74°
2.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是(
)
A.85°
B.80°
C.75°
D.70°
3.将一副三角板,如图所示放置,使点A落在DE边上,BC∥DE,AB与EF相交于点H,则∠AHF的度数为(
)
A.30°
B.45°
C.60°
D.75°
4.如图,直线AB∥CD,∠B=50°,∠C=40°,则∠E等于(
)
A.70°
B.80°
C.90°
D.100°
5.如果在△ABC中,∠A=70°-∠B,则∠C等于(???
)
A.35°????
B.70°?????
C.110°?????
D.140°
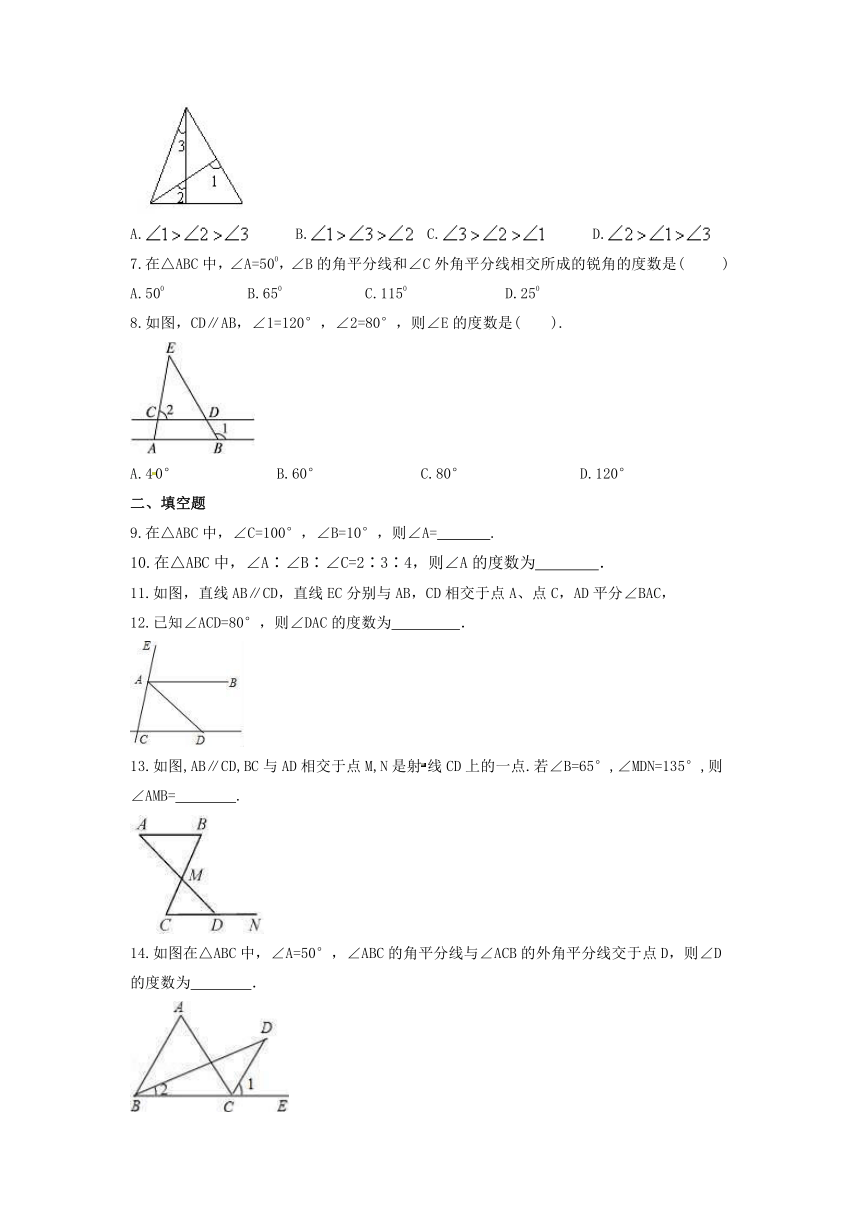
6.如图所示,的大小关系为(?????
)
A.
?
B.
C.
??
D.
7.在△ABC中,∠A=500,∠B的角平分线和∠C外角平分线相交所成的锐角的度数是(??
)
A.500?????
B.650?????
C.1150???
???D.250
8.如图,CD∥AB,∠1=120°,∠2=80°,则∠E的度数是( ).
A.40°?
?
???
B.60°?
?
???
C.80°?
?
????
D.120°
二、填空题
9.在△ABC中,∠C=100°,∠B=10°,则∠A=
.
10.在△ABC中,∠A∶∠B∶∠C=2∶3∶4,则∠A的度数为
.
11.如图,直线AB∥CD,直线EC分别与AB,CD相交于点A、点C,AD平分∠BAC,
12.已知∠ACD=80°,则∠DAC的度数为 ??
.
13.如图,AB∥CD,BC与AD相交于点M,N是射线CD上的一点.若∠B=65°,∠MDN=135°,则∠AMB=??
?
.
14.如图在△ABC中,∠A=50°,∠ABC的角平分线与∠ACB的外角平分线交于点D,则∠D的度数为 .
三、解答题
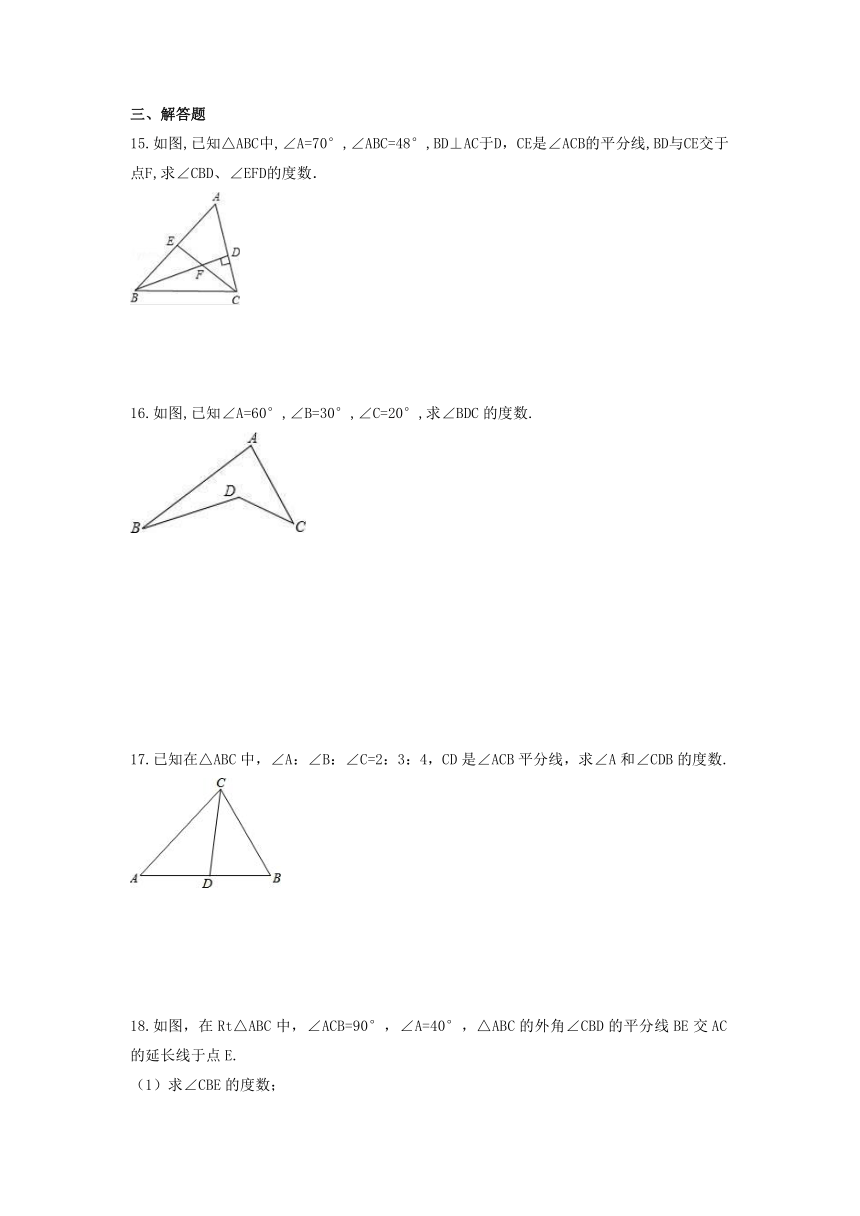
15.如图,已知△ABC中,∠A=70°,∠ABC=48°,BD⊥AC于D,CE是∠ACB的平分线,BD与CE交于点F,求∠CBD、∠EFD的度数.
16.如图,已知∠A=60°,∠B=30°,∠C=20°,求∠BDC的度数.
17.已知在△ABC中,∠A:∠B:∠C=2:3:4,CD是∠ACB平分线,求∠A和∠CDB的度数.
18.如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
参考答案
1.C.
2.A
3.D.
4.C
5.C
6.A
7.B
8.A
9.答案为:70°
10.答案为:40°.
11.答案为:50°.
12.答案为:12°
13.答案为:70°?
14.答案为:25°.
15.解:∴∠ACB=180°﹣∠A﹣∠ABC=180°﹣70°﹣48°=62°.
∵BD⊥AC,∴∠BDC=90°.∴∠CBD=90°﹣∠ACB=90°﹣62°=28°;
∵CE是∠ACB的平分线,∴∠ACE=∠ACB=×62°=31°.
∴∠EFD=∠ACE+∠BDC=31°+90°=121°.
16.解:∠BDC=110°;
17.解:∵在△ABC中,∠A:∠B:∠C=2:3:4,∠A+∠ACB+∠B=180°,
∴∠A=×180°=40°,∠ACB=×180°=80°
∵CD是∠ACB平分线,∴∠ACD=0.5∠ACB=40°
∴∠CDB=∠A+∠ACD=40°+40°=80°
18.解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,
∴∠ABC=90°-∠A=50°,
∴∠CBD=130°.
∵BE是∠CBD的平分线,
∴∠CBE=0.5∠CBD=65°;
(2)∵∠ACB=90°,∠CBE=65°,
∴∠CEB=90°-65°=25°.
∵DF∥BE,
∴∠F=∠CEB=25°.
12.2《三角形的性质》课时练习
一、选择题
1.如图,在△ABC中,点D在AB上,点E在AC上,DE∥BC.若∠A=62°,∠AED=54°,
则∠B的度数为(
)
A.54°
B.62°
C.64°
D.74°
2.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是(
)
A.85°
B.80°
C.75°
D.70°
3.将一副三角板,如图所示放置,使点A落在DE边上,BC∥DE,AB与EF相交于点H,则∠AHF的度数为(
)
A.30°
B.45°
C.60°
D.75°
4.如图,直线AB∥CD,∠B=50°,∠C=40°,则∠E等于(
)
A.70°
B.80°
C.90°
D.100°
5.如果在△ABC中,∠A=70°-∠B,则∠C等于(???
)
A.35°????
B.70°?????
C.110°?????
D.140°
6.如图所示,的大小关系为(?????
)
A.
?
B.
C.
??
D.
7.在△ABC中,∠A=500,∠B的角平分线和∠C外角平分线相交所成的锐角的度数是(??
)
A.500?????
B.650?????
C.1150???
???D.250
8.如图,CD∥AB,∠1=120°,∠2=80°,则∠E的度数是( ).
A.40°?
?
???
B.60°?
?
???
C.80°?
?
????
D.120°
二、填空题
9.在△ABC中,∠C=100°,∠B=10°,则∠A=
.
10.在△ABC中,∠A∶∠B∶∠C=2∶3∶4,则∠A的度数为
.
11.如图,直线AB∥CD,直线EC分别与AB,CD相交于点A、点C,AD平分∠BAC,
12.已知∠ACD=80°,则∠DAC的度数为 ??
.
13.如图,AB∥CD,BC与AD相交于点M,N是射线CD上的一点.若∠B=65°,∠MDN=135°,则∠AMB=??
?
.
14.如图在△ABC中,∠A=50°,∠ABC的角平分线与∠ACB的外角平分线交于点D,则∠D的度数为 .
三、解答题
15.如图,已知△ABC中,∠A=70°,∠ABC=48°,BD⊥AC于D,CE是∠ACB的平分线,BD与CE交于点F,求∠CBD、∠EFD的度数.
16.如图,已知∠A=60°,∠B=30°,∠C=20°,求∠BDC的度数.
17.已知在△ABC中,∠A:∠B:∠C=2:3:4,CD是∠ACB平分线,求∠A和∠CDB的度数.
18.如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
参考答案
1.C.
2.A
3.D.
4.C
5.C
6.A
7.B
8.A
9.答案为:70°
10.答案为:40°.
11.答案为:50°.
12.答案为:12°
13.答案为:70°?
14.答案为:25°.
15.解:∴∠ACB=180°﹣∠A﹣∠ABC=180°﹣70°﹣48°=62°.
∵BD⊥AC,∴∠BDC=90°.∴∠CBD=90°﹣∠ACB=90°﹣62°=28°;
∵CE是∠ACB的平分线,∴∠ACE=∠ACB=×62°=31°.
∴∠EFD=∠ACE+∠BDC=31°+90°=121°.
16.解:∠BDC=110°;
17.解:∵在△ABC中,∠A:∠B:∠C=2:3:4,∠A+∠ACB+∠B=180°,
∴∠A=×180°=40°,∠ACB=×180°=80°
∵CD是∠ACB平分线,∴∠ACD=0.5∠ACB=40°
∴∠CDB=∠A+∠ACD=40°+40°=80°
18.解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,
∴∠ABC=90°-∠A=50°,
∴∠CBD=130°.
∵BE是∠CBD的平分线,
∴∠CBE=0.5∠CBD=65°;
(2)∵∠ACB=90°,∠CBE=65°,
∴∠CEB=90°-65°=25°.
∵DF∥BE,
∴∠F=∠CEB=25°.
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
