2021—2022学年京改版七年级数学上册第三章简单的几何图形练习题(Word版,含答案)
文档属性
| 名称 | 2021—2022学年京改版七年级数学上册第三章简单的几何图形练习题(Word版,含答案) | 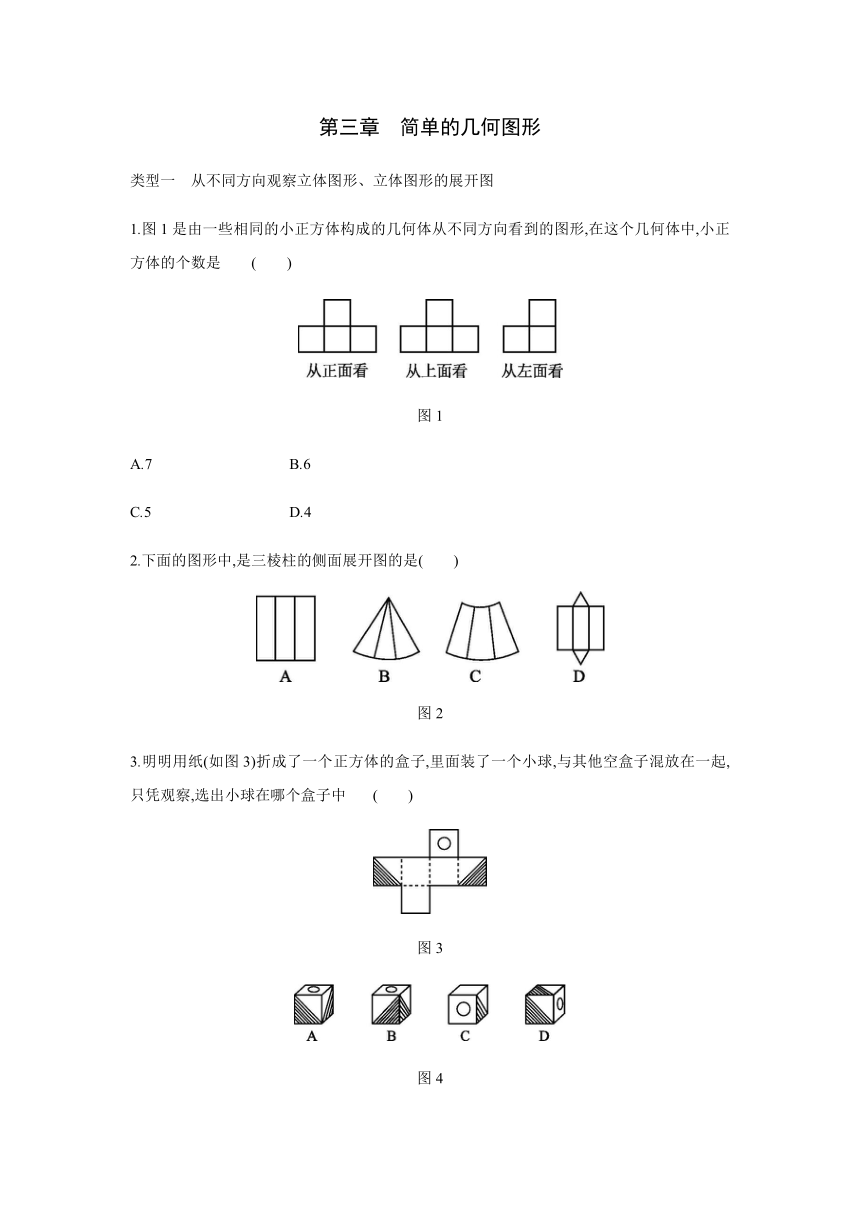 | |
| 格式 | docx | ||
| 文件大小 | 171.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 21:54:26 | ||
图片预览




文档简介
第三章 简单的几何图形
类型一 从不同方向观察立体图形、立体图形的展开图
1.图1是由一些相同的小正方体构成的几何体从不同方向看到的图形,在这个几何体中,小正方体的个数是
( )
图1
A.7
B.6
C.5
D.4
2.下面的图形中,是三棱柱的侧面展开图的是( )
图2
3.明明用纸(如图3)折成了一个正方体的盒子,里面装了一个小球,与其他空盒子混放在一起,只凭观察,选出小球在哪个盒子中
( )
图3
图4
类型二 直线、射线和线段
4.如图5,A,B,C是直线l上的三个点,图中共有线段
( )
A.1条
B.2条
C.3条
D.4条
图5
图6
5.如图6所示,下列几何语句不正确的是
( )
A.直线AB与直线BA是同一条直线
B.射线OA与射线OB是同一条射线
C.射线OA与射线AB是同一条射线
D.线段AB与线段BA是同一条线段
6.如图7,C是线段AB上的点,D是线段BC的中点.若AB=12,AC=8,则CD= .?
图7
7.在长为4.8
cm的线段AB上取一点D,使AD=AB,若C为线段AB的中点,则CD= .?
8.[2019·丰台区期末]
如图8,点C在∠AOB的边OA上,选择合适的画图工具按要求画图.
①反向延长射线OB,得到射线OD,画∠AOD的平分线OE;
②在射线OD上取一点F,使得OF=OC;
③在射线OE上作一点P,使得CP+FP最小;
④写出你完成③的作图依据: .?
图8
类型三 角
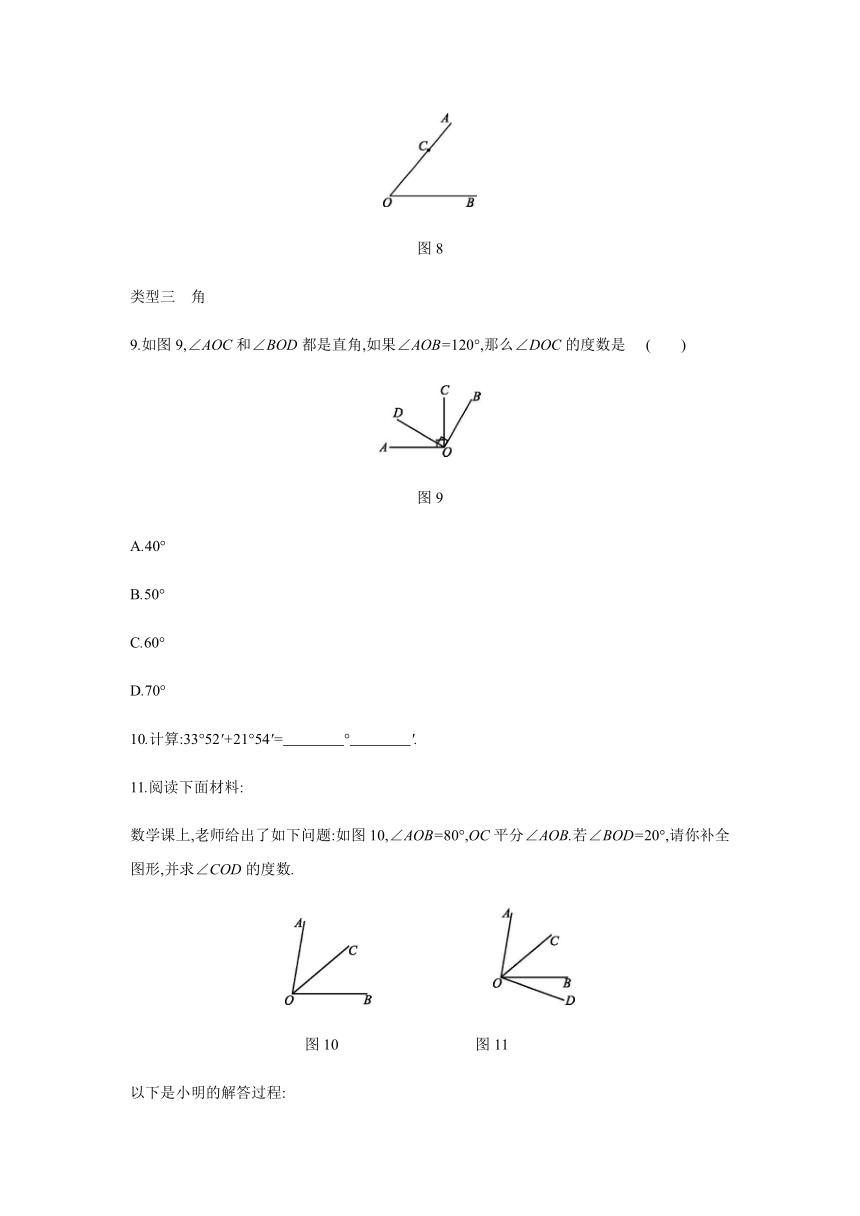
9.如图9,∠AOC和∠BOD都是直角,如果∠AOB=120°,那么∠DOC的度数是
( )
图9
A.40°
B.50°
C.60°
D.70°
10.计算:33°52'+21°54'= ° '.?
11.阅读下面材料:
数学课上,老师给出了如下问题:如图10,∠AOB=80°,OC平分∠AOB.若∠BOD=20°,请你补全图形,并求∠COD的度数.
图10
图11
以下是小明的解答过程:
解:如图11,因为OC平分∠AOB,∠AOB=80°,
所以∠BOC= ∠AOB= °.?
因为∠BOD=20°,所以∠COD= °.?
小静说:“我觉得这个题有两种情况,小明考虑的是OD在∠AOB外部的情况,事实上,OD还可能在∠AOB的内部.”
完成以下问题:
(1)请你将小明的解答过程补充完整;
(2)根据小静的想法,请你在图12中画出另一种情况对应的图形,并直接写出此时∠COD的度数为 °.?
图12
12.如图13,O是直线AB上一点,OC,OD是从点O引出的两条射线,OE平分∠AOC,∠BOC∶∠AOE∶∠AOD=2∶5∶8,求∠BOD的度数.
图13
13.如图14,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE.试求∠COE的度数.
图14
14.(1)如图15所示,∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)(2)(3)的结果你能看出什么规律?
(5)线段的计算与角的计算存在着紧密的联系,它们之间可以互相借鉴解法,请你模仿(1)~(4),设计一道以线段为背景的计算题,并写出其中的规律.
图15
类型四 两条直线的位置关系
15.
下列叙述错误的是
( )
A.经过两点有一条直线,并且只有一条直线
B.在同一平面内不相交的两条直线叫做平行线
C.连接两点的线段的长,叫做这两点间的距离
D.从直线外一点到这条直线的垂线段,叫做点到直线的距离
16.如图16,在△ABC中,∠C=90°,AC=3,P是边BC上的动点,则AP的长不可能是
( )
图16
A.2.5
B.3
C.4
D.5
17.在同一平面内,不重合的三条直线的交点有
个.?
18.如图17,∠AOC和∠DOB都是直角,如果∠DOC=35°,那么∠AOB= °.?
图17
答案
1.C [解析]
从不同方向看这个几何体,这个几何体第一层有4个小正方体,第二层有1个小正方体,放置方式如图所示.故选C.
2.A 3.B
4.C [解析]
以点A为端点的线段有2条(线段AB、线段AC),以点B为端点的线段(不含线段AB)有1条(线段BC),一共有3条线段.
5.C
6.2 [解析]
CD=(AB-AC)=2.
7.0.8
cm [解析]
如图.
因为AD=AB=×4.8=1.6(cm),AC=AB=×4.8=2.4(cm),
所以CD=AC-AD=2.4-1.6=0.8(cm).
8.解:①②③画图如图所示:
④两点之间线段最短
9.C
10.55 46 [解析]
两个度数相加,度与度,分与分对应相加,分的结果若满60,则转化为度.33°52'+21°54'=54°106'=55°46'.
11.解:(1) 40 60
(2)如图所示.
∠COD=20°.
12.解:因为OE平分∠AOC,
所以∠AOE=∠EOC.
由∠BOC∶∠AOE=2∶5,可得∠BOC∶∠AOC=2∶10,
所以∠BOC=30°.
再由∠BOC∶∠AOD=2∶8,得∠AOD=120°,
所以∠BOD=60°.
13.解:因为∠AOB=90°,OC平分∠AOB,
所以∠BOC=∠AOB=45°.
因为∠COD=90°,
所以∠BOD=∠COD-∠BOC=90°-45°=45°,
因为∠BOD=3∠DOE,
所以∠DOE=15°,
所以∠COE=∠COD-∠DOE=90°-15°=75°.
14.解:(1)因为∠AOB=90°,∠BOC=30°,
所以∠AOC=90°+30°=120°.
又因为OM平分∠AOC,
所以∠MOC=∠AOC=60°.
因为ON平分∠BOC,
所以∠NOC=∠BOC=15°,
所以∠MON=∠MOC-∠NOC=45°.
(2)因为∠AOB=α,∠BOC=30°,
所以∠AOC=α+30°.
又因为OM平分∠AOC,
所以∠MOC=∠AOC=+15°.
因为ON平分∠BOC,
所以∠NOC=∠BOC=15°,
所以∠MON=∠MOC-∠NOC=.
(3)因为∠AOB=90°,∠BOC=β,
所以∠AOC=90°+β.
又因为OM平分∠AOC,
所以∠MOC=∠AOC=+45°.
因为ON平分∠BOC,
所以∠NOC=∠BOC=,
所以∠MON=∠MOC-∠NOC=45°.
(4)从(1)(2)(3)的结果可知∠MON=∠AOB.
(5)
①如图,已知线段AB的长为26,线段BC的长为18,M是线段AC的中点,N是线段BC的中点,求线段MN的长;
②若把①中线段AB的长改为a,其余条件不变,求线段MN的长;
③若把①中线段BC的长改为b,其余条件不变,求线段MN的长;
④从①②③你能发现什么规律?
规律为MN=AB.
15.D
16.A [解析]
AC是点A到BC边上的垂线段,由垂线段最短,可知线段AP的长度应该大于或等于AC的长度.所以AP的长度不可能是2.5.
17.0或1或2或3 [解析]
因为三条直线位置不明确,所以分情况讨论:
①三条直线互相平行,有0个交点;
②一条直线与两平行线相交,有2个交点;
③三条直线都不平行,有1个或3个交点;
所以交点的个数可能为0或1或2或3.
18.145
类型一 从不同方向观察立体图形、立体图形的展开图
1.图1是由一些相同的小正方体构成的几何体从不同方向看到的图形,在这个几何体中,小正方体的个数是
( )
图1
A.7
B.6
C.5
D.4
2.下面的图形中,是三棱柱的侧面展开图的是( )
图2
3.明明用纸(如图3)折成了一个正方体的盒子,里面装了一个小球,与其他空盒子混放在一起,只凭观察,选出小球在哪个盒子中
( )
图3
图4
类型二 直线、射线和线段
4.如图5,A,B,C是直线l上的三个点,图中共有线段
( )
A.1条
B.2条
C.3条
D.4条
图5
图6
5.如图6所示,下列几何语句不正确的是
( )
A.直线AB与直线BA是同一条直线
B.射线OA与射线OB是同一条射线
C.射线OA与射线AB是同一条射线
D.线段AB与线段BA是同一条线段
6.如图7,C是线段AB上的点,D是线段BC的中点.若AB=12,AC=8,则CD= .?
图7
7.在长为4.8
cm的线段AB上取一点D,使AD=AB,若C为线段AB的中点,则CD= .?
8.[2019·丰台区期末]
如图8,点C在∠AOB的边OA上,选择合适的画图工具按要求画图.
①反向延长射线OB,得到射线OD,画∠AOD的平分线OE;
②在射线OD上取一点F,使得OF=OC;
③在射线OE上作一点P,使得CP+FP最小;
④写出你完成③的作图依据: .?
图8
类型三 角
9.如图9,∠AOC和∠BOD都是直角,如果∠AOB=120°,那么∠DOC的度数是
( )
图9
A.40°
B.50°
C.60°
D.70°
10.计算:33°52'+21°54'= ° '.?
11.阅读下面材料:
数学课上,老师给出了如下问题:如图10,∠AOB=80°,OC平分∠AOB.若∠BOD=20°,请你补全图形,并求∠COD的度数.
图10
图11
以下是小明的解答过程:
解:如图11,因为OC平分∠AOB,∠AOB=80°,
所以∠BOC= ∠AOB= °.?
因为∠BOD=20°,所以∠COD= °.?
小静说:“我觉得这个题有两种情况,小明考虑的是OD在∠AOB外部的情况,事实上,OD还可能在∠AOB的内部.”
完成以下问题:
(1)请你将小明的解答过程补充完整;
(2)根据小静的想法,请你在图12中画出另一种情况对应的图形,并直接写出此时∠COD的度数为 °.?
图12
12.如图13,O是直线AB上一点,OC,OD是从点O引出的两条射线,OE平分∠AOC,∠BOC∶∠AOE∶∠AOD=2∶5∶8,求∠BOD的度数.
图13
13.如图14,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE.试求∠COE的度数.
图14
14.(1)如图15所示,∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)(2)(3)的结果你能看出什么规律?
(5)线段的计算与角的计算存在着紧密的联系,它们之间可以互相借鉴解法,请你模仿(1)~(4),设计一道以线段为背景的计算题,并写出其中的规律.
图15
类型四 两条直线的位置关系
15.
下列叙述错误的是
( )
A.经过两点有一条直线,并且只有一条直线
B.在同一平面内不相交的两条直线叫做平行线
C.连接两点的线段的长,叫做这两点间的距离
D.从直线外一点到这条直线的垂线段,叫做点到直线的距离
16.如图16,在△ABC中,∠C=90°,AC=3,P是边BC上的动点,则AP的长不可能是
( )
图16
A.2.5
B.3
C.4
D.5
17.在同一平面内,不重合的三条直线的交点有
个.?
18.如图17,∠AOC和∠DOB都是直角,如果∠DOC=35°,那么∠AOB= °.?
图17
答案
1.C [解析]
从不同方向看这个几何体,这个几何体第一层有4个小正方体,第二层有1个小正方体,放置方式如图所示.故选C.
2.A 3.B
4.C [解析]
以点A为端点的线段有2条(线段AB、线段AC),以点B为端点的线段(不含线段AB)有1条(线段BC),一共有3条线段.
5.C
6.2 [解析]
CD=(AB-AC)=2.
7.0.8
cm [解析]
如图.
因为AD=AB=×4.8=1.6(cm),AC=AB=×4.8=2.4(cm),
所以CD=AC-AD=2.4-1.6=0.8(cm).
8.解:①②③画图如图所示:
④两点之间线段最短
9.C
10.55 46 [解析]
两个度数相加,度与度,分与分对应相加,分的结果若满60,则转化为度.33°52'+21°54'=54°106'=55°46'.
11.解:(1) 40 60
(2)如图所示.
∠COD=20°.
12.解:因为OE平分∠AOC,
所以∠AOE=∠EOC.
由∠BOC∶∠AOE=2∶5,可得∠BOC∶∠AOC=2∶10,
所以∠BOC=30°.
再由∠BOC∶∠AOD=2∶8,得∠AOD=120°,
所以∠BOD=60°.
13.解:因为∠AOB=90°,OC平分∠AOB,
所以∠BOC=∠AOB=45°.
因为∠COD=90°,
所以∠BOD=∠COD-∠BOC=90°-45°=45°,
因为∠BOD=3∠DOE,
所以∠DOE=15°,
所以∠COE=∠COD-∠DOE=90°-15°=75°.
14.解:(1)因为∠AOB=90°,∠BOC=30°,
所以∠AOC=90°+30°=120°.
又因为OM平分∠AOC,
所以∠MOC=∠AOC=60°.
因为ON平分∠BOC,
所以∠NOC=∠BOC=15°,
所以∠MON=∠MOC-∠NOC=45°.
(2)因为∠AOB=α,∠BOC=30°,
所以∠AOC=α+30°.
又因为OM平分∠AOC,
所以∠MOC=∠AOC=+15°.
因为ON平分∠BOC,
所以∠NOC=∠BOC=15°,
所以∠MON=∠MOC-∠NOC=.
(3)因为∠AOB=90°,∠BOC=β,
所以∠AOC=90°+β.
又因为OM平分∠AOC,
所以∠MOC=∠AOC=+45°.
因为ON平分∠BOC,
所以∠NOC=∠BOC=,
所以∠MON=∠MOC-∠NOC=45°.
(4)从(1)(2)(3)的结果可知∠MON=∠AOB.
(5)
①如图,已知线段AB的长为26,线段BC的长为18,M是线段AC的中点,N是线段BC的中点,求线段MN的长;
②若把①中线段AB的长改为a,其余条件不变,求线段MN的长;
③若把①中线段BC的长改为b,其余条件不变,求线段MN的长;
④从①②③你能发现什么规律?
规律为MN=AB.
15.D
16.A [解析]
AC是点A到BC边上的垂线段,由垂线段最短,可知线段AP的长度应该大于或等于AC的长度.所以AP的长度不可能是2.5.
17.0或1或2或3 [解析]
因为三条直线位置不明确,所以分情况讨论:
①三条直线互相平行,有0个交点;
②一条直线与两平行线相交,有2个交点;
③三条直线都不平行,有1个或3个交点;
所以交点的个数可能为0或1或2或3.
18.145
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
