1.4.2.2 空间中的角(2) 课件(共19张PPT)-2021-2022学年高二数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 1.4.2.2 空间中的角(2) 课件(共19张PPT)-2021-2022学年高二数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-09 20:53:37 | ||
图片预览


文档简介
(共19张PPT)
1.4.2-2
(2)
空
间
中
的
角
高二数学选择性必修第一册
第一章
空间向量与立体几何
学习目标
1.理解用向量夹角表示线线、线面、面面的夹角;
2.能用向量方法解决线线、线面、面面夹角的相关问题.
3.核心素养:数学推理、数学建模、数学运算.
l1
l2
一、回顾旧知
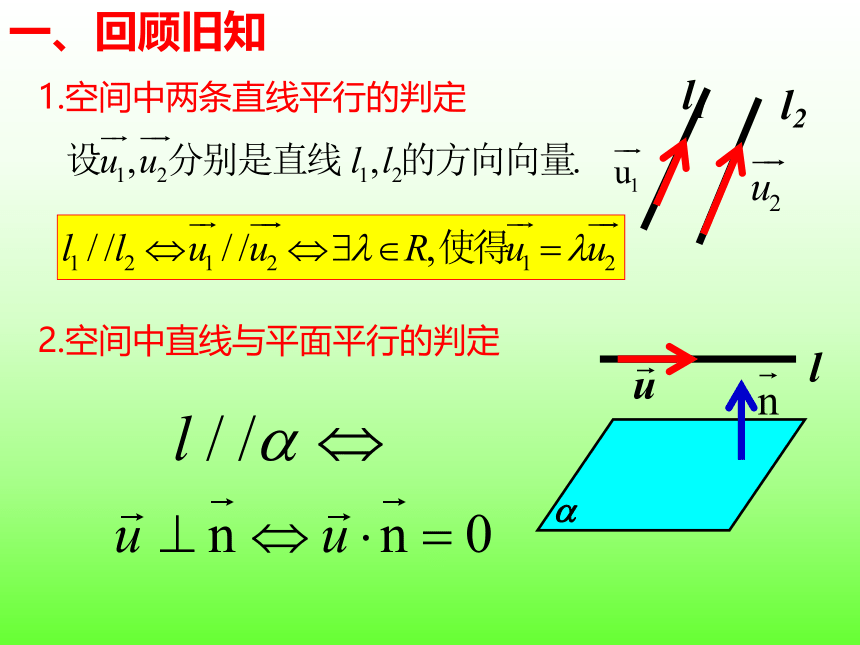
1.空间中两条直线平行的判定
2.空间中直线与平面平行的判定
l
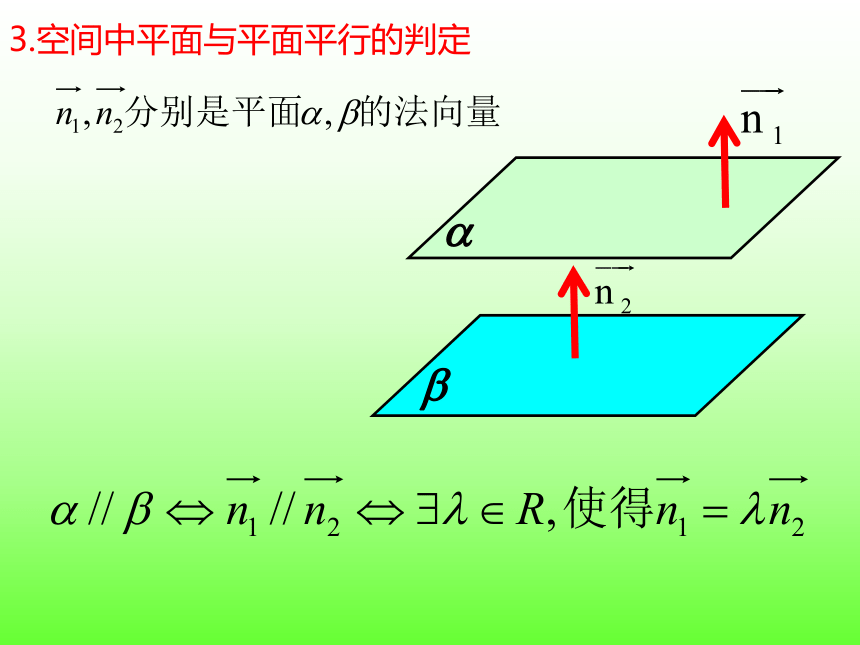
3.空间中平面与平面平行的判定
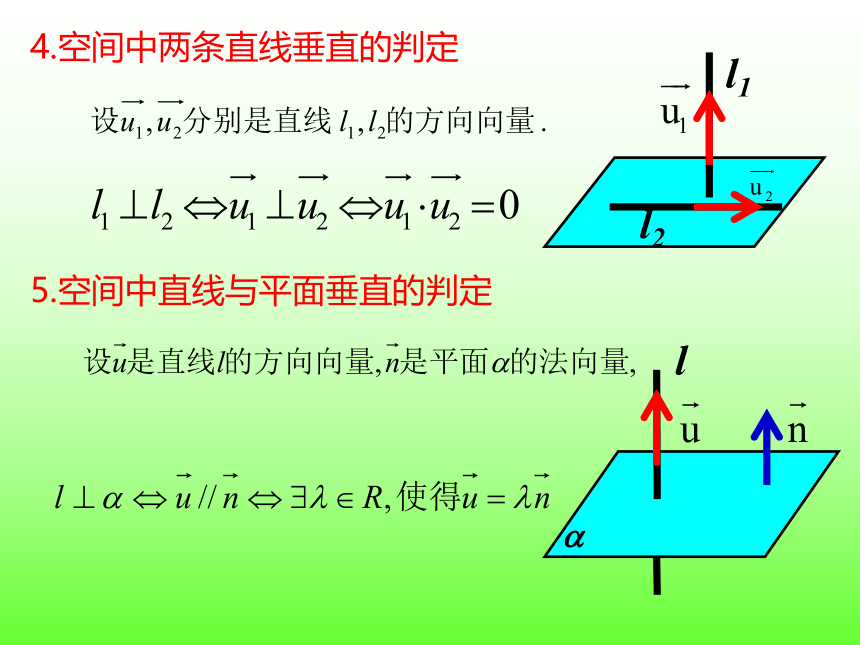
4.空间中两条直线垂直的判定
l1
l2
5.空间中直线与平面垂直的判定
l
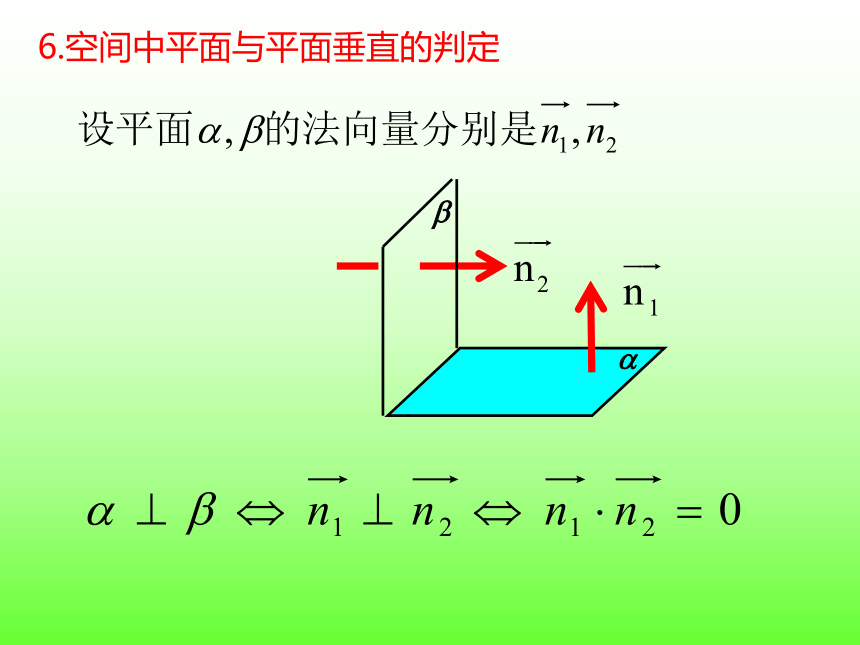
6.空间中平面与平面垂直的判定
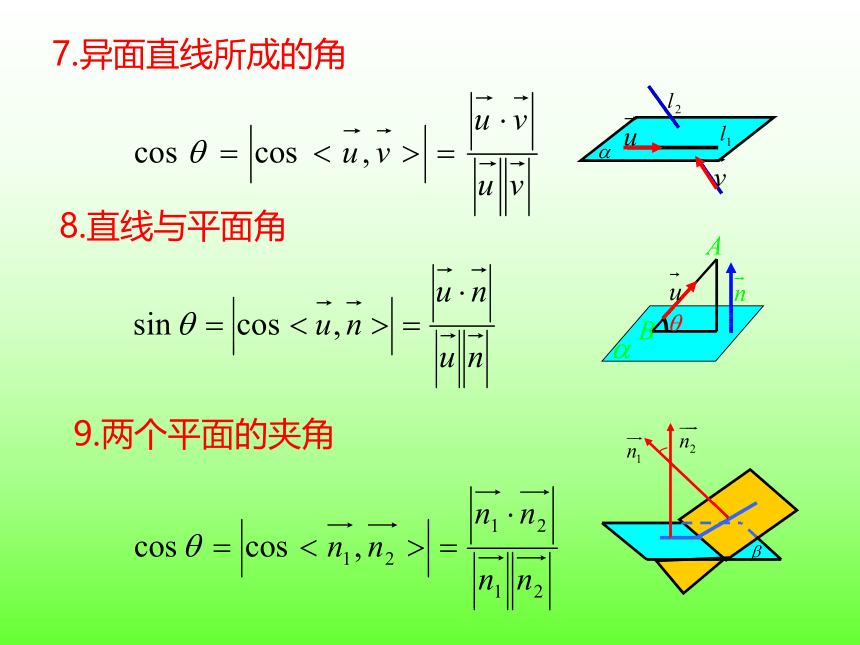
7.异面直线所成的角
8.直线与平面角
9.两个平面的夹角
二、巩固训练
1.例9.
A
B
D
P
E
F
G
解:如图所示建立空间直角坐标系,点D为坐标原点,设DC=1
(1)证明:连结AC,AC交BD于点G,连结EG
(1)求证:PA//平面EDB
2.例10.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(2)求证:PB⊥平面EFD
(3)求平面CPB与平面PBD的夹角的大小。
A
B
D
P
E
F
G
(1)求证:PA//平面EDB
2.例10.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(2)求证:PB⊥平面EFD
(3)求平面CPB与平面PBD的夹角的大小。
(1)求证:PA//平面EDB
2.例10.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(2)求证:PB⊥平面EFD
(3)求平面CPB与平面PBD的夹角的大小.
A
B
D
P
E
F
G
解:以点C为坐标原点建立空间直角坐标
系
,如图所示,设
则:
所以
与
所成角的余弦值为
3.变式:
在长方体
中,
提示:
4.变式:
的棱长为1.
正方体
x
y
z
设正方体棱长为1,
5.变式:
如图,甲站在水库底面上的点A处,乙站在水坝斜面上的点B
处.从A,B到直线
(库底与水坝的交线)的距离AC和BD分别为
和
,CD的长为
,
AB的长为
。求库底与水坝所成二面角的余弦值。
解:如图,
化为向量问题
根据向量的加法法则有
于是,得
设向量
与
的夹角为
,
就是库底与水坝所成的二面角。
因此
A
B
C
D
所以
所以库底与水坝所成二面角的余弦值为
6.变式:
化为向量问题或向量的坐标问题
进行向量运算
回到图形
7.当解空间图形问题几何法难进行时,可以尝试运用空间向量(或坐标)来处理(三步曲):
(1)建立立体图形与空间向量的联系,用空间向量表示
问题中涉及的点、直线、平面,把立体几何问题转
化为向量问题(还常建立坐标系来辅助);
(2)通过向量运算,研究点、直线、平面之间的位置关
系以及它们之间距离和夹角等问题;
(3)把向量的运算结果“翻译”成相应的几何意义.
解决立体几何问题有几种方法?
综合法、向量法、坐标法
三、课堂小结
1.异面直线所成的角
2.直线与平面所成的角
3.两个平面的夹角
(1)化为向量问题或向量的坐标问题
(2)进行向量运算
(3)回到图形
4.当解空间图形问题几何法难进行时,可以尝试运用空间向量(或坐标)来处理(三步曲):
作业:
课本P41
习题1.4
4、6题
1.4.2-2
(2)
空
间
中
的
角
高二数学选择性必修第一册
第一章
空间向量与立体几何
学习目标
1.理解用向量夹角表示线线、线面、面面的夹角;
2.能用向量方法解决线线、线面、面面夹角的相关问题.
3.核心素养:数学推理、数学建模、数学运算.
l1
l2
一、回顾旧知
1.空间中两条直线平行的判定
2.空间中直线与平面平行的判定
l
3.空间中平面与平面平行的判定
4.空间中两条直线垂直的判定
l1
l2
5.空间中直线与平面垂直的判定
l
6.空间中平面与平面垂直的判定
7.异面直线所成的角
8.直线与平面角
9.两个平面的夹角
二、巩固训练
1.例9.
A
B
D
P
E
F
G
解:如图所示建立空间直角坐标系,点D为坐标原点,设DC=1
(1)证明:连结AC,AC交BD于点G,连结EG
(1)求证:PA//平面EDB
2.例10.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(2)求证:PB⊥平面EFD
(3)求平面CPB与平面PBD的夹角的大小。
A
B
D
P
E
F
G
(1)求证:PA//平面EDB
2.例10.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(2)求证:PB⊥平面EFD
(3)求平面CPB与平面PBD的夹角的大小。
(1)求证:PA//平面EDB
2.例10.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(2)求证:PB⊥平面EFD
(3)求平面CPB与平面PBD的夹角的大小.
A
B
D
P
E
F
G
解:以点C为坐标原点建立空间直角坐标
系
,如图所示,设
则:
所以
与
所成角的余弦值为
3.变式:
在长方体
中,
提示:
4.变式:
的棱长为1.
正方体
x
y
z
设正方体棱长为1,
5.变式:
如图,甲站在水库底面上的点A处,乙站在水坝斜面上的点B
处.从A,B到直线
(库底与水坝的交线)的距离AC和BD分别为
和
,CD的长为
,
AB的长为
。求库底与水坝所成二面角的余弦值。
解:如图,
化为向量问题
根据向量的加法法则有
于是,得
设向量
与
的夹角为
,
就是库底与水坝所成的二面角。
因此
A
B
C
D
所以
所以库底与水坝所成二面角的余弦值为
6.变式:
化为向量问题或向量的坐标问题
进行向量运算
回到图形
7.当解空间图形问题几何法难进行时,可以尝试运用空间向量(或坐标)来处理(三步曲):
(1)建立立体图形与空间向量的联系,用空间向量表示
问题中涉及的点、直线、平面,把立体几何问题转
化为向量问题(还常建立坐标系来辅助);
(2)通过向量运算,研究点、直线、平面之间的位置关
系以及它们之间距离和夹角等问题;
(3)把向量的运算结果“翻译”成相应的几何意义.
解决立体几何问题有几种方法?
综合法、向量法、坐标法
三、课堂小结
1.异面直线所成的角
2.直线与平面所成的角
3.两个平面的夹角
(1)化为向量问题或向量的坐标问题
(2)进行向量运算
(3)回到图形
4.当解空间图形问题几何法难进行时,可以尝试运用空间向量(或坐标)来处理(三步曲):
作业:
课本P41
习题1.4
4、6题
