1.1.1正弦定理课件- 2021-2022学年高一下学期数学人教A版必修五(共17张PPT)
文档属性
| 名称 | 1.1.1正弦定理课件- 2021-2022学年高一下学期数学人教A版必修五(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 828.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-09 20:54:41 | ||
图片预览





文档简介
(共17张PPT)
正弦定理
宜春市第四中学——
杨洋
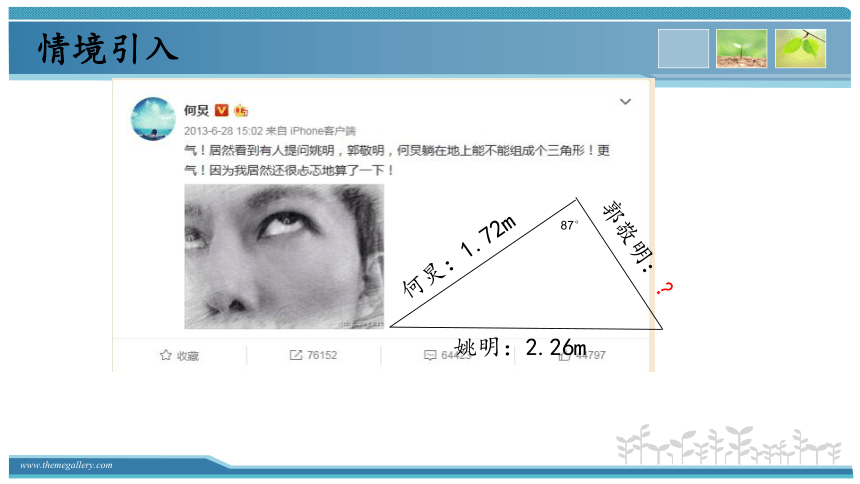
情境引入
87°
姚明:2.26m
何炅:1.72m
郭敬明:?
情境引入
A
C
B
c
b
a
问题
你有何结论?
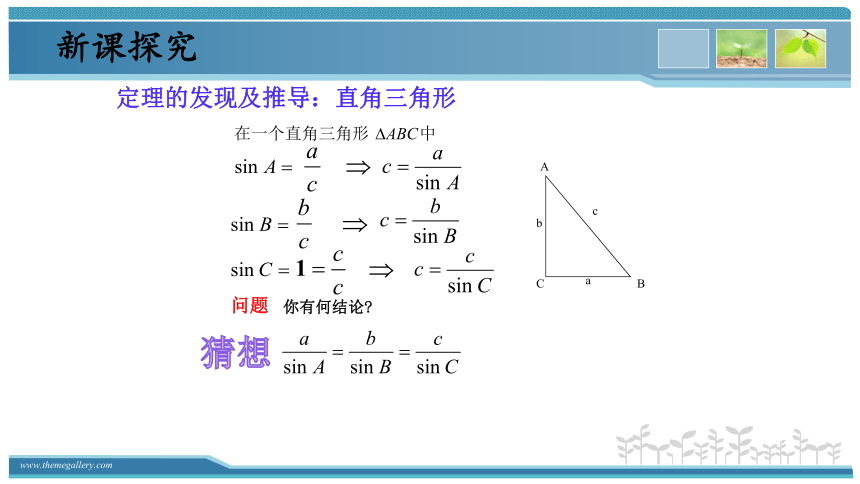
定理的发现及推导:直角三角形
新课探究
猜想
定理的推导
对一般的三角形,这个结论还能成立吗?若成立,如何证明呢?
梅文鼎老先生指出:西法用三角,犹古法之用勾股也,但三角有钝角,而勾股无之,论者遂谓勾股之数有所穷,殊不知锐角形须分为两勾股,钝角形须补成勾股知......,然则勾股虽不能备三角之形,而能兼三角之理,三角不能出勾股之外,而能尽勾股之用,一而二,二而一者也。
思考
新课探究
定理的推导:锐角三角形
当
是锐角三角形时,结论是否还成呢?
B
A
C
a
b
c
证明
如图:作AB上的高是CD,根椐
三角形的定义,得到
D
E
新课探究
探究活动:当
是钝角三角形时,以上等式是否仍然成立?如何证明?请小组讨论,展示小组成果。
定理的推导:钝角三角形
新课探究
定理的推导
当
是钝角三角形时,以上等式是否仍然成立?
B
A
C
b
c
a
D
E
新课探究
正弦定理
:
在一个三角形中,各边和它所对角的正弦的比相等,即
作用:(1)已知两边和其中一边的对角,求另外
一边的对角,进而求其他边和角
(2)已知两角和一边,求其他角和边
新课探究
新知应用
已知两角和一边
新知应用
已知两边和其中一边的对角,求其他边和角
巩固练习
回归课前提出的问题,计算出郭敬明的身高。
87°
姚明:2.26m
何炅:1.72m
郭敬明:?
A
B
C
a
b
c
巩固练习
课堂小结
预习
检测
新课讲授
巩固
训练
归纳小结
复习
导入
今天你学会了什么?
作业布置
47页练习1
拓展延伸
你还有没有其他证明正弦定理的方法吗?
=k?
授课人:杨洋
正弦定理
宜春市第四中学——
杨洋
情境引入
87°
姚明:2.26m
何炅:1.72m
郭敬明:?
情境引入
A
C
B
c
b
a
问题
你有何结论?
定理的发现及推导:直角三角形
新课探究
猜想
定理的推导
对一般的三角形,这个结论还能成立吗?若成立,如何证明呢?
梅文鼎老先生指出:西法用三角,犹古法之用勾股也,但三角有钝角,而勾股无之,论者遂谓勾股之数有所穷,殊不知锐角形须分为两勾股,钝角形须补成勾股知......,然则勾股虽不能备三角之形,而能兼三角之理,三角不能出勾股之外,而能尽勾股之用,一而二,二而一者也。
思考
新课探究
定理的推导:锐角三角形
当
是锐角三角形时,结论是否还成呢?
B
A
C
a
b
c
证明
如图:作AB上的高是CD,根椐
三角形的定义,得到
D
E
新课探究
探究活动:当
是钝角三角形时,以上等式是否仍然成立?如何证明?请小组讨论,展示小组成果。
定理的推导:钝角三角形
新课探究
定理的推导
当
是钝角三角形时,以上等式是否仍然成立?
B
A
C
b
c
a
D
E
新课探究
正弦定理
:
在一个三角形中,各边和它所对角的正弦的比相等,即
作用:(1)已知两边和其中一边的对角,求另外
一边的对角,进而求其他边和角
(2)已知两角和一边,求其他角和边
新课探究
新知应用
已知两角和一边
新知应用
已知两边和其中一边的对角,求其他边和角
巩固练习
回归课前提出的问题,计算出郭敬明的身高。
87°
姚明:2.26m
何炅:1.72m
郭敬明:?
A
B
C
a
b
c
巩固练习
课堂小结
预习
检测
新课讲授
巩固
训练
归纳小结
复习
导入
今天你学会了什么?
作业布置
47页练习1
拓展延伸
你还有没有其他证明正弦定理的方法吗?
=k?
授课人:杨洋
