2.1空间点、直线、平面之间的位置关系同步复习课讲义-2021-2022学年高一上学期人教A版数学必修2
文档属性
| 名称 | 2.1空间点、直线、平面之间的位置关系同步复习课讲义-2021-2022学年高一上学期人教A版数学必修2 |
|
|
| 格式 | docx | ||
| 文件大小 | 358.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-09 10:00:11 | ||
图片预览

文档简介
空间点、直线、平面之间的位置关系
一.四个公理
公理1:如果一条直线上的_____在一个平面内,那么这条直线在此平面内.
作用:可用来证明点、直线在平面内.
公理2:过_______________的三点,有且只有一个平面.
作用:①可用来确定一个平面;②证明点线共面.
公理2推论
推论一:一条直线和此直线外一点可以确定一个平面。
推论二:两条相交直线可以确定一个平面。
推论三:两条平行直线可以确定一个平面。
公理3:如果两个不重合的平面有一个公共点,那么它们_____________过该点的公共直线.
作用:①可用来确定两个平面的交线;②判断或证明多点共线;③判断或证明多线共点.
公理4:平行于同一条直线的两条直线_________.
作用:可用来判断空间两条直线平行.
二.空间两条直线的位置关系
(1)位置关系分类:
(2)异面直线所成的角:
①定义:设a,b是两条异面直线,经过空间任一点O作直线a′∥a,b′∥b,把a′与b′所成的_____________叫做异面直线a与b所成的角(或夹角).
②范围:_____.
三.空间直线与平面、平面与平面之间的位置关系
考题一
三点共线与三线共点问题
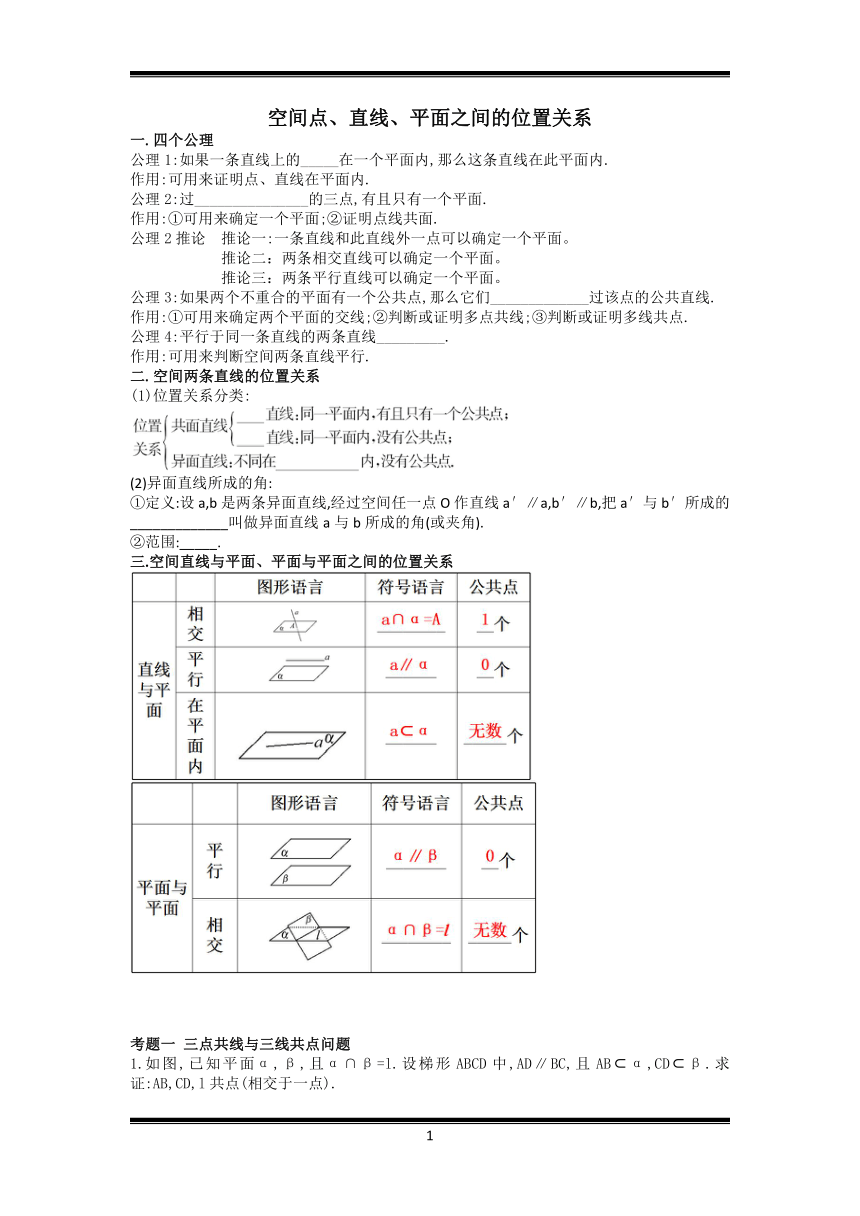
如图,已知平面α,β,且α∩β=l.设梯形ABCD中,AD∥BC,且AB?α,CD?β.求证:AB,CD,l共点(相交于一点).
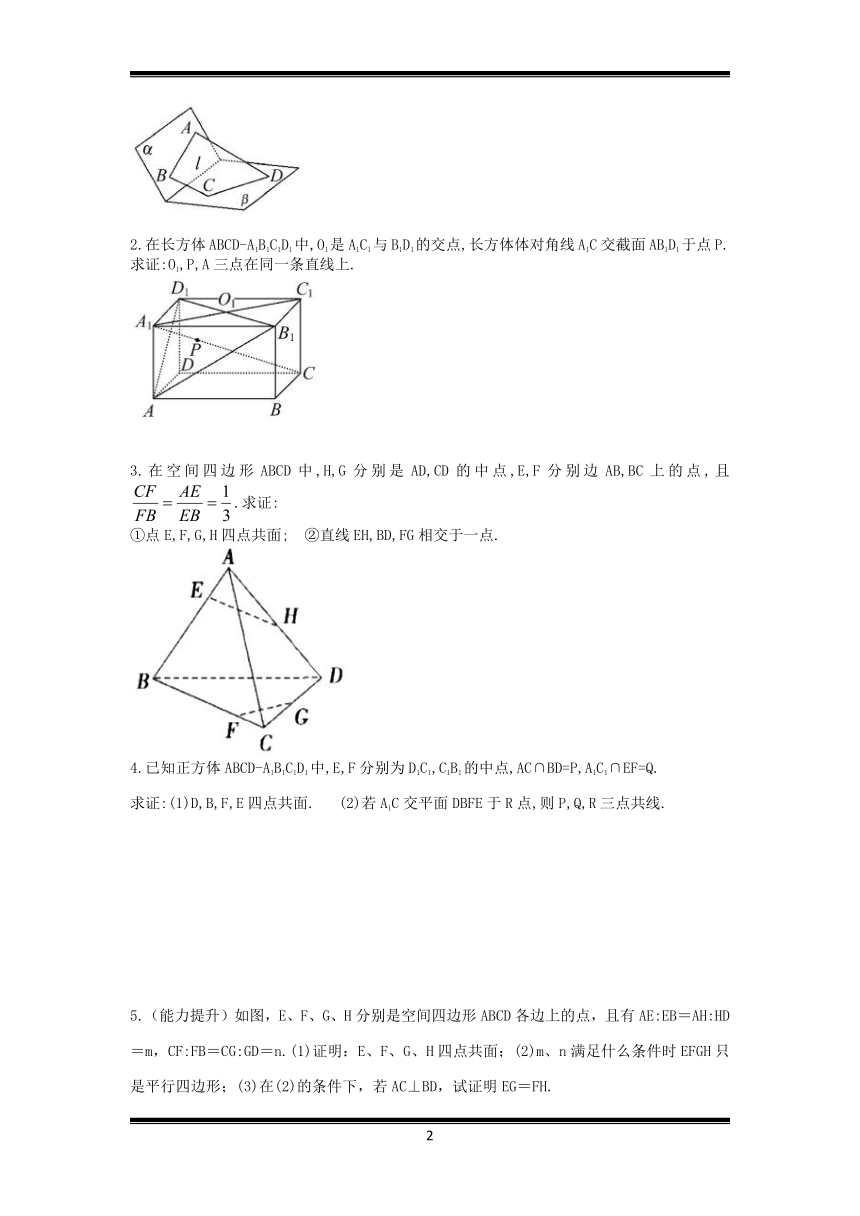
2.在长方体ABCD-A1B1C1D1中,O1是A1C1与B1D1的交点,长方体体对角线A1C交截面AB1D1于点P.求证:O1,P,A三点在同一条直线上.
3.在空间四边形ABCD中,H,G分别是AD,CD的中点,E,F分别边AB,BC上的点,且.求证:?
①点E,F,G,H四点共面;?②直线EH,BD,FG相交于一点.
4.已知正方体ABCD-A1B1C1D1中,E,F分别为D1C1,C1B1的中点,AC∩BD=P,A1C1∩EF=Q.
求证:(1)D,B,F,E四点共面.
(2)若A1C交平面DBFE于R点,则P,Q,R三点共线.
5.(能力提升)如图,E、F、G、H分别是空间四边形ABCD各边上的点,且有AE:EB=AH:HD=m,CF:FB=CG:GD=n.(1)证明:E、F、G、H四点共面;(2)m、n满足什么条件时EFGH只是平行四边形;(3)在(2)的条件下,若AC⊥BD,试证明EG=FH.
考题二
平行公理的应用
1.在正方体ABCD-A′B′C′D′中,若M,N分别是A′D′,C′D′的中点,求证:四边形ACNM是梯形.
2.如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点且AC=BD.求证:四边形EFGH是菱形.
考题三
异面直线所成的角
1.如图,在正方体ABCD-A1B1C1D1中,E,F分别是AB,AD的中点,则异面直线B1C与EF所成的角的大小为_______.
2.正方体ABCD-A′B′C′D′中,E,F分别为平面A′B′C′D′与AA′D′D的中心,求EF与CD所成的角.
3.如图,P是平面ABC外一点,,,D,E分别为PC和AB的中点,且.求异面直线PA和BC所成角的大小.
4.(能力提升)如图,三棱锥A-BCD中,AC⊥BD,E在棱AB上,F在棱CD上,并使AE∶EB=CF∶FD=m(m>0),设α为异面直线EF和AC所成的角,β为异面直线EF和BD所成的角,试求α+β的值.
考题四
直线与平面、平面与平面的位置关系
1.下列五个命题中正确命题的个数是 ( )
①如果a,b是两条直线,a∥b,那么a平行于经过b的任何一个平面;
②如果直线a和平面α满足a∥α,那么a与平面α内的任何一条直线平行;
③如果直线a,b满足a∥α,b∥α,那么a∥b;
④如果直线a,b和平面α满足a∥b,a∥α,bα,那么b∥α;
⑤如果a与平面α上的无数条直线平行,那么直线a必平行于平面α.
A.0 B.1 C.2 D.3
2.已知下列命题:
①若两个平面α∥β,a?α,b?β,则a与b是异面直线;
②若两个平面α∥β,a?α,b?β,则a与b一定不相交;
③若两个平面α∥β,a?α,b?β,则a与b平行或异面;
④若两个平面α∩β=b,a?α,则a与β一定相交.
其中正确命题的序号是_____________(将你认为正确的命题的序号都填上).
3.平面α与平面β平行,且a?α,下列四种说法中
①a与β内的所有直线都平行;
②a与β内无数条直线平行;
③a与β内的任意一条直线都不垂直;
④a与β无公共点.
其中正确的个数是 ( )
A.1
B.2
C.3
D.4
4.下列说法中错误的个数是 ( )
①两条直线都和同一个平面平行,则这两条直线平行
②两条直线没有公共点,则这两条直线平行
③两条直线都和第三条直线垂直,则这两条直线平行
④一条直线和一个平面内无数条直线没有公共点,则这条直线和这个平面平行.
A.4
B.3
C.2
D.1
1
|初一·数学·基础-提高-精英·学生版|
第1讲
第页
一.四个公理
公理1:如果一条直线上的_____在一个平面内,那么这条直线在此平面内.
作用:可用来证明点、直线在平面内.
公理2:过_______________的三点,有且只有一个平面.
作用:①可用来确定一个平面;②证明点线共面.
公理2推论
推论一:一条直线和此直线外一点可以确定一个平面。
推论二:两条相交直线可以确定一个平面。
推论三:两条平行直线可以确定一个平面。
公理3:如果两个不重合的平面有一个公共点,那么它们_____________过该点的公共直线.
作用:①可用来确定两个平面的交线;②判断或证明多点共线;③判断或证明多线共点.
公理4:平行于同一条直线的两条直线_________.
作用:可用来判断空间两条直线平行.
二.空间两条直线的位置关系
(1)位置关系分类:
(2)异面直线所成的角:
①定义:设a,b是两条异面直线,经过空间任一点O作直线a′∥a,b′∥b,把a′与b′所成的_____________叫做异面直线a与b所成的角(或夹角).
②范围:_____.
三.空间直线与平面、平面与平面之间的位置关系
考题一
三点共线与三线共点问题
如图,已知平面α,β,且α∩β=l.设梯形ABCD中,AD∥BC,且AB?α,CD?β.求证:AB,CD,l共点(相交于一点).
2.在长方体ABCD-A1B1C1D1中,O1是A1C1与B1D1的交点,长方体体对角线A1C交截面AB1D1于点P.求证:O1,P,A三点在同一条直线上.
3.在空间四边形ABCD中,H,G分别是AD,CD的中点,E,F分别边AB,BC上的点,且.求证:?
①点E,F,G,H四点共面;?②直线EH,BD,FG相交于一点.
4.已知正方体ABCD-A1B1C1D1中,E,F分别为D1C1,C1B1的中点,AC∩BD=P,A1C1∩EF=Q.
求证:(1)D,B,F,E四点共面.
(2)若A1C交平面DBFE于R点,则P,Q,R三点共线.
5.(能力提升)如图,E、F、G、H分别是空间四边形ABCD各边上的点,且有AE:EB=AH:HD=m,CF:FB=CG:GD=n.(1)证明:E、F、G、H四点共面;(2)m、n满足什么条件时EFGH只是平行四边形;(3)在(2)的条件下,若AC⊥BD,试证明EG=FH.
考题二
平行公理的应用
1.在正方体ABCD-A′B′C′D′中,若M,N分别是A′D′,C′D′的中点,求证:四边形ACNM是梯形.
2.如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点且AC=BD.求证:四边形EFGH是菱形.
考题三
异面直线所成的角
1.如图,在正方体ABCD-A1B1C1D1中,E,F分别是AB,AD的中点,则异面直线B1C与EF所成的角的大小为_______.
2.正方体ABCD-A′B′C′D′中,E,F分别为平面A′B′C′D′与AA′D′D的中心,求EF与CD所成的角.
3.如图,P是平面ABC外一点,,,D,E分别为PC和AB的中点,且.求异面直线PA和BC所成角的大小.
4.(能力提升)如图,三棱锥A-BCD中,AC⊥BD,E在棱AB上,F在棱CD上,并使AE∶EB=CF∶FD=m(m>0),设α为异面直线EF和AC所成的角,β为异面直线EF和BD所成的角,试求α+β的值.
考题四
直线与平面、平面与平面的位置关系
1.下列五个命题中正确命题的个数是 ( )
①如果a,b是两条直线,a∥b,那么a平行于经过b的任何一个平面;
②如果直线a和平面α满足a∥α,那么a与平面α内的任何一条直线平行;
③如果直线a,b满足a∥α,b∥α,那么a∥b;
④如果直线a,b和平面α满足a∥b,a∥α,bα,那么b∥α;
⑤如果a与平面α上的无数条直线平行,那么直线a必平行于平面α.
A.0 B.1 C.2 D.3
2.已知下列命题:
①若两个平面α∥β,a?α,b?β,则a与b是异面直线;
②若两个平面α∥β,a?α,b?β,则a与b一定不相交;
③若两个平面α∥β,a?α,b?β,则a与b平行或异面;
④若两个平面α∩β=b,a?α,则a与β一定相交.
其中正确命题的序号是_____________(将你认为正确的命题的序号都填上).
3.平面α与平面β平行,且a?α,下列四种说法中
①a与β内的所有直线都平行;
②a与β内无数条直线平行;
③a与β内的任意一条直线都不垂直;
④a与β无公共点.
其中正确的个数是 ( )
A.1
B.2
C.3
D.4
4.下列说法中错误的个数是 ( )
①两条直线都和同一个平面平行,则这两条直线平行
②两条直线没有公共点,则这两条直线平行
③两条直线都和第三条直线垂直,则这两条直线平行
④一条直线和一个平面内无数条直线没有公共点,则这条直线和这个平面平行.
A.4
B.3
C.2
D.1
1
|初一·数学·基础-提高-精英·学生版|
第1讲
第页
