2021-2022学年青岛版八年级数学上册1.2全等三角形的判定同步测试(Word版,含答案解析)
文档属性
| 名称 | 2021-2022学年青岛版八年级数学上册1.2全等三角形的判定同步测试(Word版,含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 366.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 22:51:11 | ||
图片预览




文档简介
数学·课课金题
初二数学上学期~青岛版
姓名
班级
座右铭
1.2全等三角形的判定
基础过关
知识点一:SAS
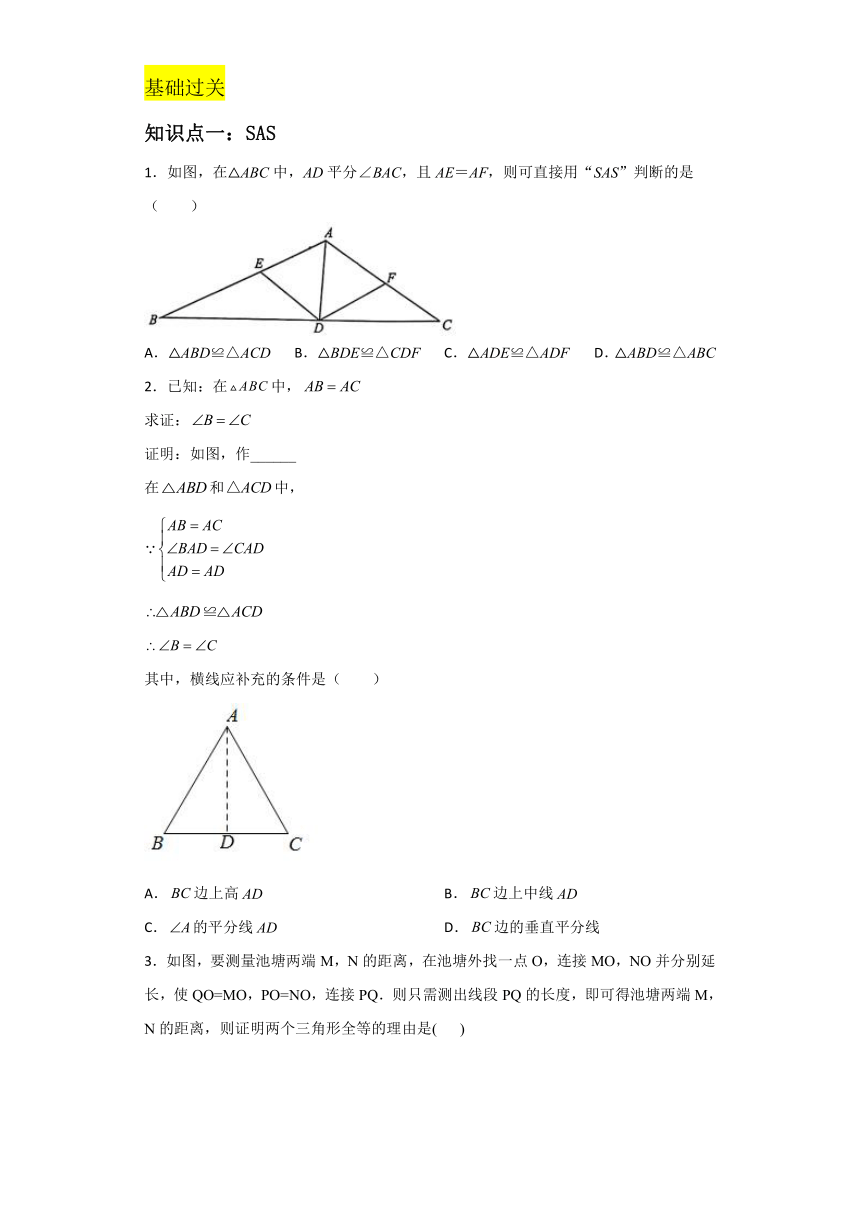
1.如图,在△ABC中,AD平分∠BAC,且AE=AF,则可直接用“SAS”判断的是( )
A.△ABD≌△ACD
B.△BDE≌△CDF
C.△ADE≌△ADF
D.△ABD≌△ABC
2.已知:在中,
求证:
证明:如图,作______
在和中,
其中,横线应补充的条件是(
)
A.边上高
B.边上中线
C.的平分线
D.边的垂直平分线
3.如图,要测量池塘两端M,N的距离,在池塘外找一点O,连接MO,NO并分别延长,使QO=MO,PO=NO,连接PQ.则只需测出线段PQ的长度,即可得池塘两端M,N的距离,则证明两个三角形全等的理由是(
??)
A.SAS
B.ASA
C.SSS
D.AAS
知识点二:AAS,ASA
4.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,添加的一组条件不正确的是( )
A.BC=DC,∠A=∠D
B.BC=EC,AC=DC
C.∠B=∠E,∠BCE=∠ACD
D.BC=EC,∠B=∠E
5.下列命题中,说法不正确的有( )个.
①形状相同的两个三角形全等;
②两边和一角对应相等的两个三角形全等;
③周长相等的两个等腰三角形全等;
④有两角及其中一角的角平分线对应相等的两个三角形全等.
A.4个
B.3个
C.2个
D.1个
6.如图,为了测量池塘两岸相对的两点A,B之间的距离,小颖在池塘外取的垂线上两点C,D,使,再画出的垂线,使点E与A,C在同一条直线上,这时,可得,因此,测得的长就是的长.这里判定的依据是(
)
A.
B.
C.
D.
7.如图所示,亮亮课本上的一个三角形被墨迹污染了一部分,很快他就根据所学知识画一出一个与这个三角形全等的图形,那么这两个三角形全等的依据是(
)
A.SSS
B.SAS
C.AAS
D.ASA
知识点三:SSS
8.小强家有两块三角形的菜地,他想判断这两块三角形菜地的形状大小是否完全一样,他设想了如下四种方法,下列方法中,不一定能判断两个三角形全等的是( )
A.测量三边对应相等
B.测量两角及其夹边对应相等
C.测量两边及除夹角外的另一角对应相等
D.测量两边及其夹角对应相等
9.如图,已知∠1=∠2,AC=AD,要使△ABC≌△AED,还需添加一个条件,那么在①AB=AE,②BC=ED;③∠C=∠D,④∠B=∠E,这四个关系中可以选择的是( )
A.1个
B.2个
C.3个
D.4个
10.在新修的花园小区中,有一条“Z”字形绿色长廊(如图),其中,在、、三段绿色长廊上各修建一凉亭、、,且是的中点,、、在一条直线上.若在凉亭与之间有一池塘,不能直接到达,要想知道与之间的距离,要测出的长度是(
)
A.
B.
C.
D.
11.已知:如图,在ABC中,∠BAC=90°,AB=AC,点D是BC边上的一点,BE⊥AD,CF⊥AD,垂足分别为E,F.下列说法:①∠EBD=∠ACF,②∠ABE=∠CAF,③EF=CF﹣BE,④ABD和CDF面积相等.正确的有( )
A.1个
B.2个
C.3个
D.4个
12.如图,在中,H是高MQ和NR的交点,且MQ=NQ,已知PQ=5,NQ=9,则MH的长为( )
A.3
B.4
C.5
D.6
13.如图,OP平分∠AOB,PC⊥OA于点C,PD⊥OB于点D,延长CP,DP交OB,OA于点E,F.下列结论错误的是( )
A.PC=PD
B.OC=OD
C.∠CPO=∠DPO
D.PC=PE
14.直尺和圆规作图(简称尺规作图)是数学定理运用的一个重要内容如图所示,作图中能得出∠A′O′B′=∠AOB的依据是运用了我们学习的全等三角形判定(
)
A.角角边
B.边角边
C.角边角
D.边边边
知识点4:HL
15.如图,用直尺和圆规作图,以点O为圆心,适当长为半径画弧,分别交OB,OA于点E、D,再分别以点E、D为圆心,大于ED的长为半径画弧,两弧交于点C,连接OC,则△ODC≌OEC的理由是( )
A.SSS
B.SAS
C.AAS
D.HL
16.如图,已知AB=AC,BD=DC,则直接能使△ABD≌△ACD的根据是( )
A.SAS
B.ASA
C.AAS
D.SSS
17.如图,∠C=∠D=90°,添加下列条件:①AC=AD;②∠ABC=∠ABD;③BC=BD,其中能判定Rt△ABC与Rt△ABD全等的条件有( )
A.0个
B.1个
C.2个
D.3个
18.如图,在中,于点,分别交,于点,,,若依据“”说明,则下列所添条件合理的是(
)
A.
B.
C.
D.
19.如图,已知在和中,,,下列条件中不能判定的是(
)
A.
B.
C.且
D.
20.如图,,,,则能直接判断的理由是(
)
A.
B.
C.
D.
21.如图所示,∠C=∠D=90°,添加下列条件①AC=AD;②∠ABC=∠ABD;③∠BAC=∠BAD;④BC=BD,能判定Rt△ABC与Rt△ABD
全等的条件的个数是(
)
A.1
B.2
C.3
D.4
综合达标
22.有两个三角形,分别为和其中,.
(1)若按图①所示位置摆放,使得与重合,连接,则与CE
的数量关系是__________;
(2)在图①中延长BD交CE于点,如图②所示,求的度数;
(3)若按图③所示位置摆放,连接且与交于点F,请判断与之间的关系,并说明理由
23.如图1,∠ABC=90°,FA⊥AB于点A,D是线段AB上的点,AD=BC,AF=BD.
(1)判断DF与DC的数量关系为
,位置关系为
.
(2)如图2,若点D在线段AB的延长线上,过点A在AB的另一侧作AF⊥AB,并截取AF=BD,连接DC、DF、CF,试说明(1)中结论是否成立,并说明理由.
(3)若点D在线段AB外,点E是BC延长线上一点,且CE=BD,连接AE,与DC的延长线交于点P,直接写出∠APC的度数.
24.如图,AB∥DE,B,C,D三点在同一条直线上,∠A=90°,EC⊥BD,且AB=CD.求证:AC=CE.
25.如图,点A、E、F、B在同一条直线上,且AE=BF,AC∥BD,∠C=∠D.求证:DE∥CF.
26.已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作等边△ADE(顶点A、D、E按逆时针方向排列),连接CE.
(1)如图,当点D在边BC上时,求证:①△ABD≌△ACE,②AC=CE+CD;
(2)当点D不在边BC上时,其他条件不变,请写出AC、CE、CD之间存在的数量关系.
试卷第1页,总3页
1.2参考答案与试题解析
1.C
解:∵AD平分∠BAC,
∴∠EAD=∠FAD,
在△ADE与△ADF中,
,
∴△ADE≌△ADF(SAS),
故选:C.
2.C
【解析】
证明:如图,作的平分线
在和中,
故选C
3.A
【解析】
解:在△PQO和△NMO中,
,
∴△PQO≌△NMO(SAS),
故选:A.
4.A
【解析】
解:A.AB=DE,BC=DC,∠A=∠D,不符合全等三角形的判定定理,不能推出△ABC≌△DEC,故本选项符合题意;
B.AC=DC,AB=DE,BC=EC,符合全等三角形的判定定理SSS,能推出△ABC≌△DEC,故本选项不符合题意;
C.∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD+∠ACE,
即∠ACB=∠DCE,
∵∠B=∠E,AB=DE,
∴△ABC≌△DEC(AAS),故本选项不符合题意;
D.AB=DE,∠B=∠E,BC=EC,符合全等三角形的判定定理SAS,能推出△ABC≌△DEC,故本选项不符合题意;
故选:A.
B
6.A
7.D
【解析】
解:画一个三角形A′B′C′,使∠A′=∠A,A′B′=AB,∠B′=∠B,
符合全等三角形的判定定理ASA,
8.C
【解析】
解:全等三角形的判定方法有:SSS,SAS,ASA,AAS;
A:根据SSS,两个三角形全等;
B:根据ASA,两个三角形全等;
C:两个三角形不一定不全等;
D:根据SAS,两个三角形全等;
故选:C.
9.C
【解析】
解:,
,
,
①当时,可根据“”判断,符合题意;
②当时,不能判断,不符合题意;
③当时,可根据“”判断,符合题意;
④当时,可根据“”判断,符合题意,
故有3个可选,
故选:C.
10.A
【解析】
解:∵AB∥CD
∴∠B=∠C,∠BEM=∠CFM
∵M是BC的中点
∴BM=CM
∴△EMB≌△FMC(AAS)
∴EM=FM
∴只需要测量出EM的长度即可
故选A.
11.B
【解析】
解:∵BE⊥AD,CF⊥AD,
∴BE∥CF,
∴∠EBD=∠DCF,
故①不正确;
∵∠BAC=90°,且BE⊥AD,CF⊥AD,
∴∠ABE+∠BAE=∠BAE+∠FAC,
∴∠ABE=∠FAC;
在△ABE与△CAF中,
,
∴△ABE≌△CAF(AAS),
∴BE=AF,AE=CF,∠ABE=∠CAF,
∴EF=CF﹣BE,
故②③正确.
无法判断△ABD和△CDF面积相等,故④不正确.
12.B
【解析】
解:∵MQ⊥PN,NR⊥PM,
∴∠NQH=∠NRP=∠HRM=90,
∵∠RHM=∠QHN,
∴∠PMH=∠HNQ,
在和中,
,
∴(ASA),
∴PQ=QH=5,
∵NQ=MQ=9,
∴MH=MQ﹣HQ=9﹣5=4,
13.D
【解析】
解:∵OP平分∠AOB,
∴∠POD=∠POC,
∵PD⊥OB,PC⊥OA,
∴∠PCO=∠PDO,
在△POD和△POC中,
,
∴△POC≌△POD(AAS),
∴PC=PD,OC=OD,∠CPO=∠DPO,故A,B,C正确;
故选:D.
14.D
【详解】
解:由作图可知,OD=OC=OD′=OC′,CD=C′D′.
在△COD和△C′O′D′中,
,
∴△COD≌△C′O′D′(SSS),
∴∠AOB=∠A′O′B′,
故选:D.
15.A
【解析】
如图,连接EC、DC.
根据作图的过程知,OE=OD,CE=CD,
在△EOC与△DOC中,
,
∴△EOC≌△DOC(SSS).
16.D
17.D
【解析】
解:∵∠C=∠D=90°,AB=AB,
∴①AC=AD,可用HL判定Rt△ABC与Rt△ABD全等;
②∠ABC=∠ABD,可用AAS判定Rt△ABC与Rt△ABD全等;
③BC=BD,可用HL判定Rt△ABC与Rt△ABD全等;
18.D
19.D
【解析】
解:A、若,则根据“SSS”可判定,故不符合题意;
B、若,则根据“SAS”可判定,故不符合题意;
C、若且,则根据“HL”可判定,故不符合题意;
D、若,则不能判定,故符合题意;
故选D.
20.A
【详解】
解:在Rt△ABD和Rt△CDB中,
∴Rt△ABD≌Rt△CDB(HL),
21.D
【解析】
∵∠C=∠D=90°,AB=AB,
∴①AC=AD,可用HL判定Rt△ABC与Rt△ABD全等;
②∠ABC=∠ABD,可用AAS判定Rt△ABC与Rt△ABD全等;
③∠BAC=∠BAD,可用AAS判定Rt△ABC与Rt△ABD全等;
④BC=BD,可用HL判定Rt△ABC与Rt△ABD全等;
故选:D.
22.【解析】
解:(1)在△DAB和△EAC中,
,
∴△DAB≌△EAC(SAS),
∴BD=CE;
故答案为BD=CE;
(2)∵△DAB≌△EAC,
∴∠ECA=∠DBA,
∵∠FDC=∠ADB,
∴∠CFD=∠DAB=90°,
∴∠BFC=90°;
(3)BD与CE相互垂直,BD=CE.
理由如下:∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
在△DAB和△EAC中,
,
∴△DAB≌△EAC(SAS),
∴∠ABD=∠ACE,BD=CE,
∵∠BAC=90°,
∴∠CBF+∠BCF=∠ABC+∠ACB=90°,
∴∠BFC=90°,
∴BD⊥CE.
23.解:(1)∵AF⊥AB,
∴∠DAF=90°,
在△ADF和△BCD中,
,
∴△ADF≌△BCD(SAS),
∴DF=CD,∠ADF=∠BCD,
∵∠BCD+∠CDB=90°,
∴∠ADF+∠CDB=90°,即∠CDF=90°,
∴CD⊥DF.
故答案为:DF=CD,CD⊥DF;
(2)成立,理由如下:
∵AF⊥AB,
∴∠DAF=90°,
在△ADF和△BCD中,
,
∴△ADF≌△BCD(SAS),
∴DF=CD,∠ADF=∠BCD,
∵∠BCD+∠CDB=90°,
∴∠ADF+∠CDB=90°,即∠CDF=90°,
∴CD⊥DF;
(3)如图,由题意,过点A作AF⊥AB,并截取AF=BD,连接DF,CF,AC,
由(1)得△CDF为等腰直角三角形,
∴∠DCF=45°,
∵∠FAD=∠ABC=90°,
∴AF∥CE,
∴∠FAC=∠ACE,
∵AF=BD,CE=BD,
∴AF=CE,又AC=AC,
∴△AFC≌△CEA(SAS),
∴∠CAE=∠ACF,
∴FC∥AE,
∴∠APC=∠FCD,
∴∠APC=∠FCD=45°.
24.证明:∵AB∥DE,
∴∠B=∠D,
∵EC⊥BD,∠A=90°,
∴∠DCE=90°=∠A,
在△ABC和△CDE中,
,
∴△ABC≌△CDE(ASA),
∴AC=CE.
25.证明:∵AE=BF,
∴AE+EF=BF+EF,
∴AF=BE,
∵AC∥DB,
∴∠A=∠B,
在△ACF和△BDE中,
,
∴△ACF≌△BDE(AAS),
∴∠AFC=∠BED,
∴DE∥CF.
26.(1)证明:①∵△ABC和△ADE都是等边三角形,
∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°.
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,即∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS);
②∵△ABD≌△ACE,
∴BD=CE,
∵BC=BD+CD,AC=BC,
∴AC=CE+CD;
(2)解:如图2,当点D在边BC的延长线上时,AC=CE﹣CD,
理由如下:∵△ABC和△ADE都是等边三角形,
∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴CE﹣CD=BD﹣CD=BC=AC,
∴AC=CE﹣CD;
如图3,当点D在边CB的延长线上时,AC=CD﹣CE,
理由如下:同(2)的方法可证,△ABD≌△ACE(SAS),
∴BD=CE.
∵BC=CD﹣BD=CD﹣CE,
∴AC=CD﹣CE,
综上所述,点D在边BC的延长线上,AC=CE﹣CD;点D在边CB的延长线上,AC=CD﹣CE
二维码至此处
初二数学上学期~青岛版
姓名
班级
座右铭
1.2全等三角形的判定
基础过关
知识点一:SAS
1.如图,在△ABC中,AD平分∠BAC,且AE=AF,则可直接用“SAS”判断的是( )
A.△ABD≌△ACD
B.△BDE≌△CDF
C.△ADE≌△ADF
D.△ABD≌△ABC
2.已知:在中,
求证:
证明:如图,作______
在和中,
其中,横线应补充的条件是(
)
A.边上高
B.边上中线
C.的平分线
D.边的垂直平分线
3.如图,要测量池塘两端M,N的距离,在池塘外找一点O,连接MO,NO并分别延长,使QO=MO,PO=NO,连接PQ.则只需测出线段PQ的长度,即可得池塘两端M,N的距离,则证明两个三角形全等的理由是(
??)
A.SAS
B.ASA
C.SSS
D.AAS
知识点二:AAS,ASA
4.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,添加的一组条件不正确的是( )
A.BC=DC,∠A=∠D
B.BC=EC,AC=DC
C.∠B=∠E,∠BCE=∠ACD
D.BC=EC,∠B=∠E
5.下列命题中,说法不正确的有( )个.
①形状相同的两个三角形全等;
②两边和一角对应相等的两个三角形全等;
③周长相等的两个等腰三角形全等;
④有两角及其中一角的角平分线对应相等的两个三角形全等.
A.4个
B.3个
C.2个
D.1个
6.如图,为了测量池塘两岸相对的两点A,B之间的距离,小颖在池塘外取的垂线上两点C,D,使,再画出的垂线,使点E与A,C在同一条直线上,这时,可得,因此,测得的长就是的长.这里判定的依据是(
)
A.
B.
C.
D.
7.如图所示,亮亮课本上的一个三角形被墨迹污染了一部分,很快他就根据所学知识画一出一个与这个三角形全等的图形,那么这两个三角形全等的依据是(
)
A.SSS
B.SAS
C.AAS
D.ASA
知识点三:SSS
8.小强家有两块三角形的菜地,他想判断这两块三角形菜地的形状大小是否完全一样,他设想了如下四种方法,下列方法中,不一定能判断两个三角形全等的是( )
A.测量三边对应相等
B.测量两角及其夹边对应相等
C.测量两边及除夹角外的另一角对应相等
D.测量两边及其夹角对应相等
9.如图,已知∠1=∠2,AC=AD,要使△ABC≌△AED,还需添加一个条件,那么在①AB=AE,②BC=ED;③∠C=∠D,④∠B=∠E,这四个关系中可以选择的是( )
A.1个
B.2个
C.3个
D.4个
10.在新修的花园小区中,有一条“Z”字形绿色长廊(如图),其中,在、、三段绿色长廊上各修建一凉亭、、,且是的中点,、、在一条直线上.若在凉亭与之间有一池塘,不能直接到达,要想知道与之间的距离,要测出的长度是(
)
A.
B.
C.
D.
11.已知:如图,在ABC中,∠BAC=90°,AB=AC,点D是BC边上的一点,BE⊥AD,CF⊥AD,垂足分别为E,F.下列说法:①∠EBD=∠ACF,②∠ABE=∠CAF,③EF=CF﹣BE,④ABD和CDF面积相等.正确的有( )
A.1个
B.2个
C.3个
D.4个
12.如图,在中,H是高MQ和NR的交点,且MQ=NQ,已知PQ=5,NQ=9,则MH的长为( )
A.3
B.4
C.5
D.6
13.如图,OP平分∠AOB,PC⊥OA于点C,PD⊥OB于点D,延长CP,DP交OB,OA于点E,F.下列结论错误的是( )
A.PC=PD
B.OC=OD
C.∠CPO=∠DPO
D.PC=PE
14.直尺和圆规作图(简称尺规作图)是数学定理运用的一个重要内容如图所示,作图中能得出∠A′O′B′=∠AOB的依据是运用了我们学习的全等三角形判定(
)
A.角角边
B.边角边
C.角边角
D.边边边
知识点4:HL
15.如图,用直尺和圆规作图,以点O为圆心,适当长为半径画弧,分别交OB,OA于点E、D,再分别以点E、D为圆心,大于ED的长为半径画弧,两弧交于点C,连接OC,则△ODC≌OEC的理由是( )
A.SSS
B.SAS
C.AAS
D.HL
16.如图,已知AB=AC,BD=DC,则直接能使△ABD≌△ACD的根据是( )
A.SAS
B.ASA
C.AAS
D.SSS
17.如图,∠C=∠D=90°,添加下列条件:①AC=AD;②∠ABC=∠ABD;③BC=BD,其中能判定Rt△ABC与Rt△ABD全等的条件有( )
A.0个
B.1个
C.2个
D.3个
18.如图,在中,于点,分别交,于点,,,若依据“”说明,则下列所添条件合理的是(
)
A.
B.
C.
D.
19.如图,已知在和中,,,下列条件中不能判定的是(
)
A.
B.
C.且
D.
20.如图,,,,则能直接判断的理由是(
)
A.
B.
C.
D.
21.如图所示,∠C=∠D=90°,添加下列条件①AC=AD;②∠ABC=∠ABD;③∠BAC=∠BAD;④BC=BD,能判定Rt△ABC与Rt△ABD
全等的条件的个数是(
)
A.1
B.2
C.3
D.4
综合达标
22.有两个三角形,分别为和其中,.
(1)若按图①所示位置摆放,使得与重合,连接,则与CE
的数量关系是__________;
(2)在图①中延长BD交CE于点,如图②所示,求的度数;
(3)若按图③所示位置摆放,连接且与交于点F,请判断与之间的关系,并说明理由
23.如图1,∠ABC=90°,FA⊥AB于点A,D是线段AB上的点,AD=BC,AF=BD.
(1)判断DF与DC的数量关系为
,位置关系为
.
(2)如图2,若点D在线段AB的延长线上,过点A在AB的另一侧作AF⊥AB,并截取AF=BD,连接DC、DF、CF,试说明(1)中结论是否成立,并说明理由.
(3)若点D在线段AB外,点E是BC延长线上一点,且CE=BD,连接AE,与DC的延长线交于点P,直接写出∠APC的度数.
24.如图,AB∥DE,B,C,D三点在同一条直线上,∠A=90°,EC⊥BD,且AB=CD.求证:AC=CE.
25.如图,点A、E、F、B在同一条直线上,且AE=BF,AC∥BD,∠C=∠D.求证:DE∥CF.
26.已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作等边△ADE(顶点A、D、E按逆时针方向排列),连接CE.
(1)如图,当点D在边BC上时,求证:①△ABD≌△ACE,②AC=CE+CD;
(2)当点D不在边BC上时,其他条件不变,请写出AC、CE、CD之间存在的数量关系.
试卷第1页,总3页
1.2参考答案与试题解析
1.C
解:∵AD平分∠BAC,
∴∠EAD=∠FAD,
在△ADE与△ADF中,
,
∴△ADE≌△ADF(SAS),
故选:C.
2.C
【解析】
证明:如图,作的平分线
在和中,
故选C
3.A
【解析】
解:在△PQO和△NMO中,
,
∴△PQO≌△NMO(SAS),
故选:A.
4.A
【解析】
解:A.AB=DE,BC=DC,∠A=∠D,不符合全等三角形的判定定理,不能推出△ABC≌△DEC,故本选项符合题意;
B.AC=DC,AB=DE,BC=EC,符合全等三角形的判定定理SSS,能推出△ABC≌△DEC,故本选项不符合题意;
C.∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD+∠ACE,
即∠ACB=∠DCE,
∵∠B=∠E,AB=DE,
∴△ABC≌△DEC(AAS),故本选项不符合题意;
D.AB=DE,∠B=∠E,BC=EC,符合全等三角形的判定定理SAS,能推出△ABC≌△DEC,故本选项不符合题意;
故选:A.
B
6.A
7.D
【解析】
解:画一个三角形A′B′C′,使∠A′=∠A,A′B′=AB,∠B′=∠B,
符合全等三角形的判定定理ASA,
8.C
【解析】
解:全等三角形的判定方法有:SSS,SAS,ASA,AAS;
A:根据SSS,两个三角形全等;
B:根据ASA,两个三角形全等;
C:两个三角形不一定不全等;
D:根据SAS,两个三角形全等;
故选:C.
9.C
【解析】
解:,
,
,
①当时,可根据“”判断,符合题意;
②当时,不能判断,不符合题意;
③当时,可根据“”判断,符合题意;
④当时,可根据“”判断,符合题意,
故有3个可选,
故选:C.
10.A
【解析】
解:∵AB∥CD
∴∠B=∠C,∠BEM=∠CFM
∵M是BC的中点
∴BM=CM
∴△EMB≌△FMC(AAS)
∴EM=FM
∴只需要测量出EM的长度即可
故选A.
11.B
【解析】
解:∵BE⊥AD,CF⊥AD,
∴BE∥CF,
∴∠EBD=∠DCF,
故①不正确;
∵∠BAC=90°,且BE⊥AD,CF⊥AD,
∴∠ABE+∠BAE=∠BAE+∠FAC,
∴∠ABE=∠FAC;
在△ABE与△CAF中,
,
∴△ABE≌△CAF(AAS),
∴BE=AF,AE=CF,∠ABE=∠CAF,
∴EF=CF﹣BE,
故②③正确.
无法判断△ABD和△CDF面积相等,故④不正确.
12.B
【解析】
解:∵MQ⊥PN,NR⊥PM,
∴∠NQH=∠NRP=∠HRM=90,
∵∠RHM=∠QHN,
∴∠PMH=∠HNQ,
在和中,
,
∴(ASA),
∴PQ=QH=5,
∵NQ=MQ=9,
∴MH=MQ﹣HQ=9﹣5=4,
13.D
【解析】
解:∵OP平分∠AOB,
∴∠POD=∠POC,
∵PD⊥OB,PC⊥OA,
∴∠PCO=∠PDO,
在△POD和△POC中,
,
∴△POC≌△POD(AAS),
∴PC=PD,OC=OD,∠CPO=∠DPO,故A,B,C正确;
故选:D.
14.D
【详解】
解:由作图可知,OD=OC=OD′=OC′,CD=C′D′.
在△COD和△C′O′D′中,
,
∴△COD≌△C′O′D′(SSS),
∴∠AOB=∠A′O′B′,
故选:D.
15.A
【解析】
如图,连接EC、DC.
根据作图的过程知,OE=OD,CE=CD,
在△EOC与△DOC中,
,
∴△EOC≌△DOC(SSS).
16.D
17.D
【解析】
解:∵∠C=∠D=90°,AB=AB,
∴①AC=AD,可用HL判定Rt△ABC与Rt△ABD全等;
②∠ABC=∠ABD,可用AAS判定Rt△ABC与Rt△ABD全等;
③BC=BD,可用HL判定Rt△ABC与Rt△ABD全等;
18.D
19.D
【解析】
解:A、若,则根据“SSS”可判定,故不符合题意;
B、若,则根据“SAS”可判定,故不符合题意;
C、若且,则根据“HL”可判定,故不符合题意;
D、若,则不能判定,故符合题意;
故选D.
20.A
【详解】
解:在Rt△ABD和Rt△CDB中,
∴Rt△ABD≌Rt△CDB(HL),
21.D
【解析】
∵∠C=∠D=90°,AB=AB,
∴①AC=AD,可用HL判定Rt△ABC与Rt△ABD全等;
②∠ABC=∠ABD,可用AAS判定Rt△ABC与Rt△ABD全等;
③∠BAC=∠BAD,可用AAS判定Rt△ABC与Rt△ABD全等;
④BC=BD,可用HL判定Rt△ABC与Rt△ABD全等;
故选:D.
22.【解析】
解:(1)在△DAB和△EAC中,
,
∴△DAB≌△EAC(SAS),
∴BD=CE;
故答案为BD=CE;
(2)∵△DAB≌△EAC,
∴∠ECA=∠DBA,
∵∠FDC=∠ADB,
∴∠CFD=∠DAB=90°,
∴∠BFC=90°;
(3)BD与CE相互垂直,BD=CE.
理由如下:∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
在△DAB和△EAC中,
,
∴△DAB≌△EAC(SAS),
∴∠ABD=∠ACE,BD=CE,
∵∠BAC=90°,
∴∠CBF+∠BCF=∠ABC+∠ACB=90°,
∴∠BFC=90°,
∴BD⊥CE.
23.解:(1)∵AF⊥AB,
∴∠DAF=90°,
在△ADF和△BCD中,
,
∴△ADF≌△BCD(SAS),
∴DF=CD,∠ADF=∠BCD,
∵∠BCD+∠CDB=90°,
∴∠ADF+∠CDB=90°,即∠CDF=90°,
∴CD⊥DF.
故答案为:DF=CD,CD⊥DF;
(2)成立,理由如下:
∵AF⊥AB,
∴∠DAF=90°,
在△ADF和△BCD中,
,
∴△ADF≌△BCD(SAS),
∴DF=CD,∠ADF=∠BCD,
∵∠BCD+∠CDB=90°,
∴∠ADF+∠CDB=90°,即∠CDF=90°,
∴CD⊥DF;
(3)如图,由题意,过点A作AF⊥AB,并截取AF=BD,连接DF,CF,AC,
由(1)得△CDF为等腰直角三角形,
∴∠DCF=45°,
∵∠FAD=∠ABC=90°,
∴AF∥CE,
∴∠FAC=∠ACE,
∵AF=BD,CE=BD,
∴AF=CE,又AC=AC,
∴△AFC≌△CEA(SAS),
∴∠CAE=∠ACF,
∴FC∥AE,
∴∠APC=∠FCD,
∴∠APC=∠FCD=45°.
24.证明:∵AB∥DE,
∴∠B=∠D,
∵EC⊥BD,∠A=90°,
∴∠DCE=90°=∠A,
在△ABC和△CDE中,
,
∴△ABC≌△CDE(ASA),
∴AC=CE.
25.证明:∵AE=BF,
∴AE+EF=BF+EF,
∴AF=BE,
∵AC∥DB,
∴∠A=∠B,
在△ACF和△BDE中,
,
∴△ACF≌△BDE(AAS),
∴∠AFC=∠BED,
∴DE∥CF.
26.(1)证明:①∵△ABC和△ADE都是等边三角形,
∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°.
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,即∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS);
②∵△ABD≌△ACE,
∴BD=CE,
∵BC=BD+CD,AC=BC,
∴AC=CE+CD;
(2)解:如图2,当点D在边BC的延长线上时,AC=CE﹣CD,
理由如下:∵△ABC和△ADE都是等边三角形,
∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴CE﹣CD=BD﹣CD=BC=AC,
∴AC=CE﹣CD;
如图3,当点D在边CB的延长线上时,AC=CD﹣CE,
理由如下:同(2)的方法可证,△ABD≌△ACE(SAS),
∴BD=CE.
∵BC=CD﹣BD=CD﹣CE,
∴AC=CD﹣CE,
综上所述,点D在边BC的延长线上,AC=CE﹣CD;点D在边CB的延长线上,AC=CD﹣CE
二维码至此处
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
