24.4.1几何图形问题课时训练卷(Word版 含答案) 2021-2022学年冀教版九年级数学上册
文档属性
| 名称 | 24.4.1几何图形问题课时训练卷(Word版 含答案) 2021-2022学年冀教版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 169.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 08:11:12 | ||
图片预览


文档简介
冀教版九年级数学上册
24.4.1
几何图形问题
课时训练卷
一、选择题(共8小题,4
8=32)
1.
某中学准备建一个面积为5
000
m2的矩形操场,操场的长比宽长50
m,设操场的长为x
m,根据题意,下面所列方程正确的是( )
A.x(x-50)=5
000
B.x(x+50)=5
000
C.2x(x-25)=5
000
D.2x(x+25)=5
000
2.
某小区在规划设计时,准备在两幢楼房之间,设置一块面积为900平方米的矩形绿地,并且长比宽多10米.设绿地的宽为x米,根据题意,可列方程为( )
A.x(x-10)=900
B.x(x+10)=900
C.10(x+10)=900
D.2[x+(x+10)]=900
3.
今年我市计划扩大城区绿地面积,现有一块矩形绿地,它的短边长为60
m,若将短边增大到与长边相等(长边不变),使扩大后的绿地的形状是正方形,则扩大后的绿地面积比原来增加1600
m2,设扩大后的正方形绿地边长为x
m,下面所列方程正确的是(
)
A.x(x-60)=1600
B.x(x+60)=1600
C.60(x+60)=1600
D.60(x-60)=1600
4.
如图,把一块长为40
cm、宽为30
cm的矩形硬纸板的四角剪去四个相同的小正方形,然后把纸板沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为600
cm2,设剪去的小正方形的边长为x
cm,则可列方程为( )
A.(30-2x)(40-x)=600
B.(30-x)(40-x)=600
C.(30-x)(40-2x)=600
D.(30-2x)(40-2x)=600
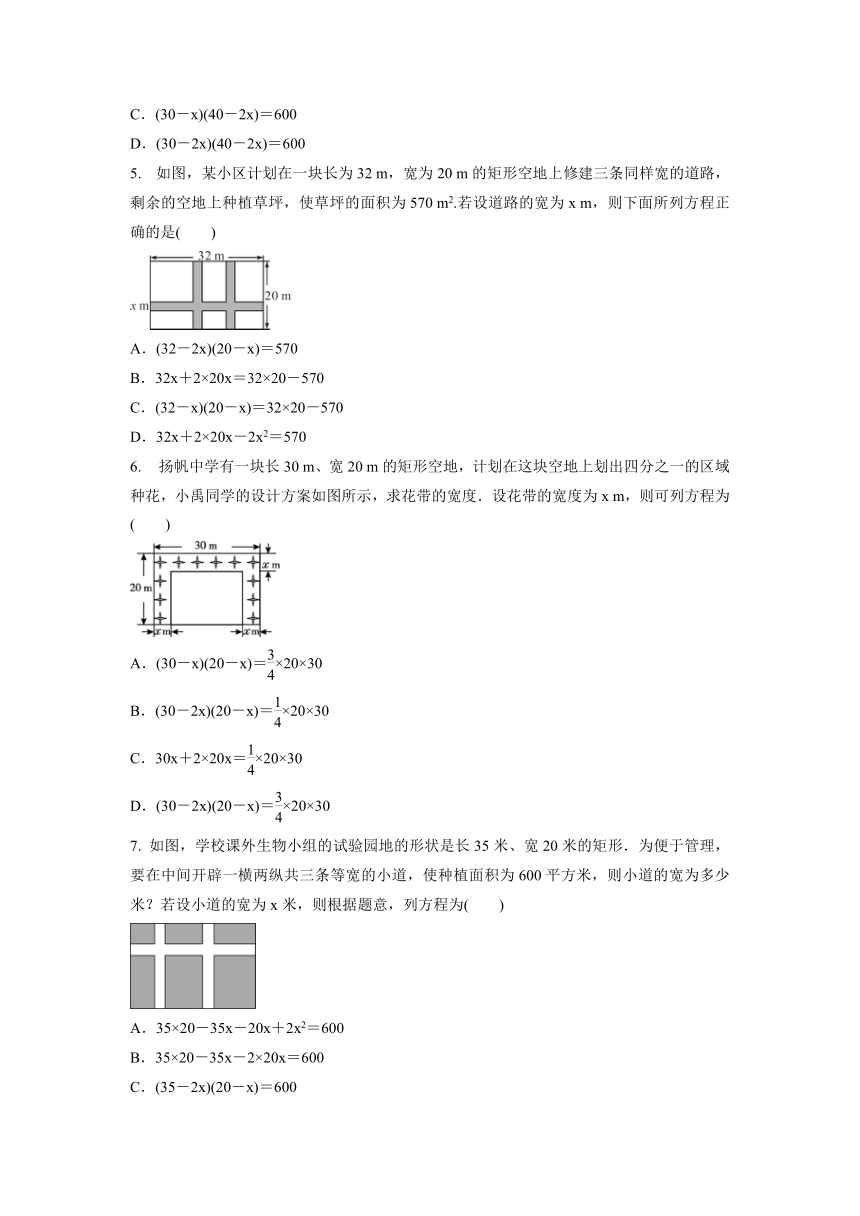
5.
如图,某小区计划在一块长为32
m,宽为20
m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570
m2.若设道路的宽为x
m,则下面所列方程正确的是( )
A.(32-2x)(20-x)=570
B.32x+2×20x=32×20-570
C.(32-x)(20-x)=32×20-570
D.32x+2×20x-2x2=570
6.
扬帆中学有一块长30
m、宽20
m的矩形空地,计划在这块空地上划出四分之一的区域种花,小禹同学的设计方案如图所示,求花带的宽度.设花带的宽度为x
m,则可列方程为( )
A.(30-x)(20-x)=×20×30
B.(30-2x)(20-x)=×20×30
C.30x+2×20x=×20×30
D.(30-2x)(20-x)=×20×30
7.
如图,学校课外生物小组的试验园地的形状是长35米、宽20米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为600平方米,则小道的宽为多少米?若设小道的宽为x米,则根据题意,列方程为(
)
A.35×20-35x-20x+2x2=600
B.35×20-35x-2×20x=600
C.(35-2x)(20-x)=600
D.(35-x)(20-2x)=600
8.
如图,在宽为20
m,长为32
m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540
m2,求道路的宽.如果设小路宽为x
m,根据题意,所列方程正确的是( )
A.(20-x)(32-x)=540
B.(20-x)(32-x)=100
C.(20+x)(32-x)=540
D.(20-x)(32+x)=540
二.填空题(共6小题,4
6=24)
9.如图,在一块长35
m、宽26
m的矩形绿地上有宽度相同的两条小路,其中绿地面积为850
m2,求小路的宽.设小路宽为x
m,则可列方程为____________________.
10.
如图,某小区有一块面积为120
m2且靠墙(墙足够长)的矩形空地ABCD,为美化环境,用总长为100
m的篱笆围成四块矩形花圃(靠墙一侧不用篱笆,篱笆的厚度不计).设BC的长度为x
m,若四块矩形花圃的面积相等,则可列方程为__________________.
11.
一块矩形铁皮长为4
dm,宽为3
dm,在四角各截去一个面积相等的正方形,做成一个无盖的盒子,要使盒子的底面积是原来铁皮的面积的一半,若设盒子的高为x
dm,根据题意列出方程,并化成一般形式是_____________.
12.如图,在长为100米,宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644平方米,则道路的宽应为多少米?设道路的宽为x米,则可列方程为_______________________________.
13.
如图,在宽为20
m,长为30
m的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551
m2,则修建的路宽应为_________m.
14.
如图是一张长12
cm,宽10
cm的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余部分(阴影部分)可制成底面积是24
cm2的有盖的长方体铁盒.则剪去的正方形的边长为_________cm.
三.解答题(共5小题,
44分)
15.(6分)
改善小区环境,争创文明家园.如图所示,某社区决定在一块长(AD)16
m,宽(AB)9
m的矩形场地ABCD上修建三条同样宽的小路,其中两条与AB平行,另一条与AD平行,其余部分种草.要使草坪部分的总面积为112
m2,则小路的宽应为多少?
16.(8分)
已知长方形硬纸板ABCD的长BC为40
cm,宽CD为30
cm,按如图所示的方式剪掉2个小正方形和2个小长方形(即阴影部分)后,将剩余部分折成一个有盖的长方体盒子,设剪掉的小正方形的边长为x
cm.(纸板的厚度忽略不计)若折成的长方体盒子的表面积为950
cm2,求该长方体盒子的体积.
17.(8分)
如图,在△ABC中,∠B=90°,点P从点A开始,沿AB边向点B以1
cm/s的速度移动,点Q从点B开始沿BC边向点C以2
cm/s的速度移动.如果点P,Q分别从点A,B同时出发,经过几秒钟,使△PBQ的面积等于8
cm2?
18.(10分)
某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600
m2的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35
m,另外三面用69
m长的篱笆围成,其中一边开有一扇1
m宽的门(不包括篱笆).求这个茶园的长和宽.
19.(12分)
小林准备进行如下操作试验:把一根长为40
cm的铁丝剪成两段,并把每一段各围成一个正方形.
(1)要使这两个正方形的面积之和等于58
cm2,小林该怎么剪?
(2)小峰对小林说:“这两个正方形的面积之和不可能等于48
cm2.”他的说法对吗?请说明理由.
参考答案
1-4ABAD
5-8ADCA
9.
(35-x)(26-x)=850
10.
x=120
11.
2x2-7x+3=0
12.
(100-x)(80-x)=7644
13.
1
14.
2
15.
解:设小路的宽应为x
m,根据题意,得(16-2x)(9-x)=112,解得x1=1,x2=16.∵16>9,∴x=16不符合题意,舍去,∴x=1.答:小路的宽应为1
m.
16.
解:根据题意,得40×30-2x2-2×
x=950,解得x1=5,x2=-25(不合题意,舍去),所以30-2x=20,20-x=15,所以该长方体盒子的体积为5×20×15=1
500(cm3).
17.
解:设经过x秒钟,△PBQ的面积等于8
cm2,依题意得(6-x)·2x=8,即x2-6x+8=0,解得x1=2,x2=4,答:经过2秒钟或4秒钟,△PBQ的面积等于8
cm2.
18.
解:设茶园垂直于墙的一边长为x
m,则另一边的长度为(69+1-2x)m,根据题意,得x(69+1-2x)=
600,整理,得x2-35x+300=0,解得x1=15,x2=20.
当x=15时,70-2x=40>35,不符合题意,舍去;当x=20时,70-2x=30,符合题意.答:这个茶园的长和宽分别为30
m,20
m.
19.
解:(1)设其中一个正方形的边长为x
cm,依题意列方程x2+(10-x)2=58,解得x1=3,x2=7,∴分成12
cm和28
cm.
(2)他的说法对,由x2+(10-x)2=48,即x2-10x+26=0,∵Δ=-4<0,∴该方程无实数解,∴小峰的说法对.
24.4.1
几何图形问题
课时训练卷
一、选择题(共8小题,4
8=32)
1.
某中学准备建一个面积为5
000
m2的矩形操场,操场的长比宽长50
m,设操场的长为x
m,根据题意,下面所列方程正确的是( )
A.x(x-50)=5
000
B.x(x+50)=5
000
C.2x(x-25)=5
000
D.2x(x+25)=5
000
2.
某小区在规划设计时,准备在两幢楼房之间,设置一块面积为900平方米的矩形绿地,并且长比宽多10米.设绿地的宽为x米,根据题意,可列方程为( )
A.x(x-10)=900
B.x(x+10)=900
C.10(x+10)=900
D.2[x+(x+10)]=900
3.
今年我市计划扩大城区绿地面积,现有一块矩形绿地,它的短边长为60
m,若将短边增大到与长边相等(长边不变),使扩大后的绿地的形状是正方形,则扩大后的绿地面积比原来增加1600
m2,设扩大后的正方形绿地边长为x
m,下面所列方程正确的是(
)
A.x(x-60)=1600
B.x(x+60)=1600
C.60(x+60)=1600
D.60(x-60)=1600
4.
如图,把一块长为40
cm、宽为30
cm的矩形硬纸板的四角剪去四个相同的小正方形,然后把纸板沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为600
cm2,设剪去的小正方形的边长为x
cm,则可列方程为( )
A.(30-2x)(40-x)=600
B.(30-x)(40-x)=600
C.(30-x)(40-2x)=600
D.(30-2x)(40-2x)=600
5.
如图,某小区计划在一块长为32
m,宽为20
m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570
m2.若设道路的宽为x
m,则下面所列方程正确的是( )
A.(32-2x)(20-x)=570
B.32x+2×20x=32×20-570
C.(32-x)(20-x)=32×20-570
D.32x+2×20x-2x2=570
6.
扬帆中学有一块长30
m、宽20
m的矩形空地,计划在这块空地上划出四分之一的区域种花,小禹同学的设计方案如图所示,求花带的宽度.设花带的宽度为x
m,则可列方程为( )
A.(30-x)(20-x)=×20×30
B.(30-2x)(20-x)=×20×30
C.30x+2×20x=×20×30
D.(30-2x)(20-x)=×20×30
7.
如图,学校课外生物小组的试验园地的形状是长35米、宽20米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为600平方米,则小道的宽为多少米?若设小道的宽为x米,则根据题意,列方程为(
)
A.35×20-35x-20x+2x2=600
B.35×20-35x-2×20x=600
C.(35-2x)(20-x)=600
D.(35-x)(20-2x)=600
8.
如图,在宽为20
m,长为32
m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540
m2,求道路的宽.如果设小路宽为x
m,根据题意,所列方程正确的是( )
A.(20-x)(32-x)=540
B.(20-x)(32-x)=100
C.(20+x)(32-x)=540
D.(20-x)(32+x)=540
二.填空题(共6小题,4
6=24)
9.如图,在一块长35
m、宽26
m的矩形绿地上有宽度相同的两条小路,其中绿地面积为850
m2,求小路的宽.设小路宽为x
m,则可列方程为____________________.
10.
如图,某小区有一块面积为120
m2且靠墙(墙足够长)的矩形空地ABCD,为美化环境,用总长为100
m的篱笆围成四块矩形花圃(靠墙一侧不用篱笆,篱笆的厚度不计).设BC的长度为x
m,若四块矩形花圃的面积相等,则可列方程为__________________.
11.
一块矩形铁皮长为4
dm,宽为3
dm,在四角各截去一个面积相等的正方形,做成一个无盖的盒子,要使盒子的底面积是原来铁皮的面积的一半,若设盒子的高为x
dm,根据题意列出方程,并化成一般形式是_____________.
12.如图,在长为100米,宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644平方米,则道路的宽应为多少米?设道路的宽为x米,则可列方程为_______________________________.
13.
如图,在宽为20
m,长为30
m的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551
m2,则修建的路宽应为_________m.
14.
如图是一张长12
cm,宽10
cm的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余部分(阴影部分)可制成底面积是24
cm2的有盖的长方体铁盒.则剪去的正方形的边长为_________cm.
三.解答题(共5小题,
44分)
15.(6分)
改善小区环境,争创文明家园.如图所示,某社区决定在一块长(AD)16
m,宽(AB)9
m的矩形场地ABCD上修建三条同样宽的小路,其中两条与AB平行,另一条与AD平行,其余部分种草.要使草坪部分的总面积为112
m2,则小路的宽应为多少?
16.(8分)
已知长方形硬纸板ABCD的长BC为40
cm,宽CD为30
cm,按如图所示的方式剪掉2个小正方形和2个小长方形(即阴影部分)后,将剩余部分折成一个有盖的长方体盒子,设剪掉的小正方形的边长为x
cm.(纸板的厚度忽略不计)若折成的长方体盒子的表面积为950
cm2,求该长方体盒子的体积.
17.(8分)
如图,在△ABC中,∠B=90°,点P从点A开始,沿AB边向点B以1
cm/s的速度移动,点Q从点B开始沿BC边向点C以2
cm/s的速度移动.如果点P,Q分别从点A,B同时出发,经过几秒钟,使△PBQ的面积等于8
cm2?
18.(10分)
某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600
m2的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35
m,另外三面用69
m长的篱笆围成,其中一边开有一扇1
m宽的门(不包括篱笆).求这个茶园的长和宽.
19.(12分)
小林准备进行如下操作试验:把一根长为40
cm的铁丝剪成两段,并把每一段各围成一个正方形.
(1)要使这两个正方形的面积之和等于58
cm2,小林该怎么剪?
(2)小峰对小林说:“这两个正方形的面积之和不可能等于48
cm2.”他的说法对吗?请说明理由.
参考答案
1-4ABAD
5-8ADCA
9.
(35-x)(26-x)=850
10.
x=120
11.
2x2-7x+3=0
12.
(100-x)(80-x)=7644
13.
1
14.
2
15.
解:设小路的宽应为x
m,根据题意,得(16-2x)(9-x)=112,解得x1=1,x2=16.∵16>9,∴x=16不符合题意,舍去,∴x=1.答:小路的宽应为1
m.
16.
解:根据题意,得40×30-2x2-2×
x=950,解得x1=5,x2=-25(不合题意,舍去),所以30-2x=20,20-x=15,所以该长方体盒子的体积为5×20×15=1
500(cm3).
17.
解:设经过x秒钟,△PBQ的面积等于8
cm2,依题意得(6-x)·2x=8,即x2-6x+8=0,解得x1=2,x2=4,答:经过2秒钟或4秒钟,△PBQ的面积等于8
cm2.
18.
解:设茶园垂直于墙的一边长为x
m,则另一边的长度为(69+1-2x)m,根据题意,得x(69+1-2x)=
600,整理,得x2-35x+300=0,解得x1=15,x2=20.
当x=15时,70-2x=40>35,不符合题意,舍去;当x=20时,70-2x=30,符合题意.答:这个茶园的长和宽分别为30
m,20
m.
19.
解:(1)设其中一个正方形的边长为x
cm,依题意列方程x2+(10-x)2=58,解得x1=3,x2=7,∴分成12
cm和28
cm.
(2)他的说法对,由x2+(10-x)2=48,即x2-10x+26=0,∵Δ=-4<0,∴该方程无实数解,∴小峰的说法对.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
