2021-2022学年人教版九年级数学上册 21.2.4一元二次方程的根与系数的关系课件(共26张)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册 21.2.4一元二次方程的根与系数的关系课件(共26张) |  | |
| 格式 | zip | ||
| 文件大小 | 298.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 08:13:53 | ||
图片预览







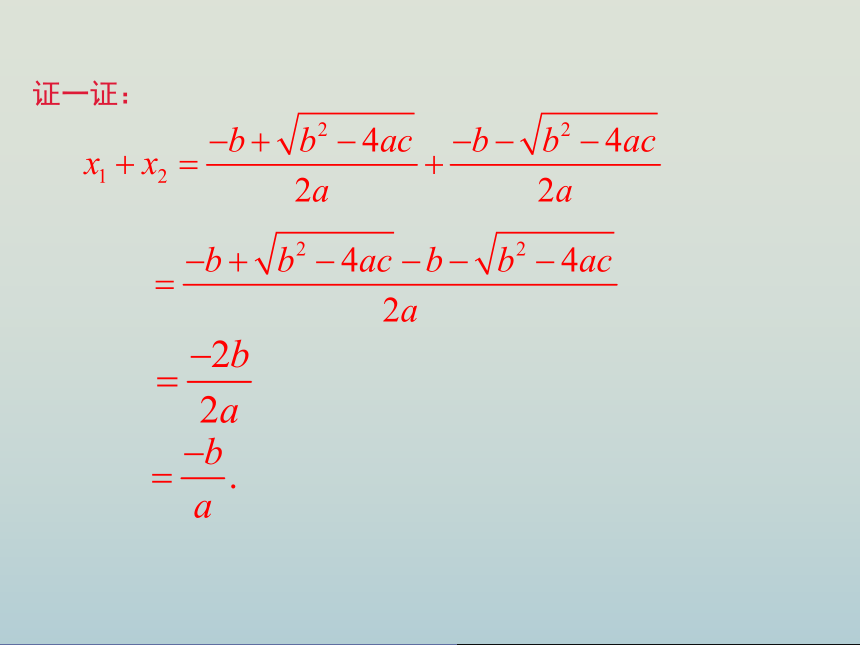
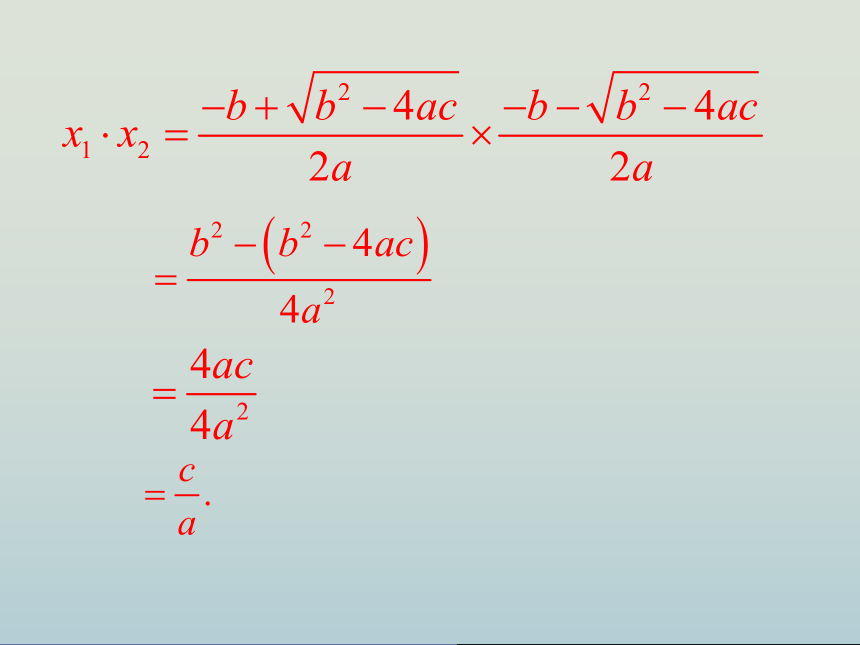
文档简介
(共26张PPT)
第二十一章
一元二次方程
21.2.4
一元二次方程的根与系数的关系
【学习目标】
1.掌握一元二次方程根与系数的关系(韦达定理);
2.掌握运用韦达定理求出方程的一根与方程中的未知系数,能求出与两根有关的一些代数式的值。
复习引入
1.一元二次方程的求根公式是什么?
2.方程的两根x1和x2与系数a,b,c还有其它关系吗?
【学习探究】
方程
的求根公式
,不仅表示可以由方程的系数a,b,c决定根的值,而且反应了根
与系数之间的联系.
新课引入
一元二次方程的根与系数的关系
算一算
解下列方程并完成填空:
(1)x2+3x-4=0;
(2)x2-5x+6=0;
(3)2x2+3x+1=0.
一元二次方程
两
根
关
系
x1
x2
x2+3x-4=0
x2-5x+6=0
2x2+3x+1=0
-4
1
2
3
-1
x1+x2=-3
x1
·
x2=-4
x1+x2=5
x1
·
x2=6
猜一猜
(1)若一元二次方程的两根为x1,x2,则有x-x1=0,且x-x2=0,那么方程(x-x1)(x-x2)=0(x1,x2为已知数)的两根是什么?将方程化为x2+px+q=0的形式,你能看出x1,x2与p,q之间的关系吗?
重要发现
如果方程x2+px+q=0的两根是x1,x2,那么x1+x2=
-p
,x1
·x2=q.
(x-x1)(x-x2)=0.
x2-(x1+x2)x+x1·x2=0,
x2+px+q=0,
x1+x2=
-p
,x1
·x2=q.
猜一猜
(2)如果一元二次方程
ax2+bx+c=0(a≠0)的两个根分别是x1、
x2,那么,你可以发现什么结论?
证一证:
一元二次方程的根与系数的关系
(韦达定理)
如果一元二次方程
ax2+bx+c=0(a≠0)的两个根分别是x1、
x2,那么
注意
满足上述关系的前提条件
b2-4ac≥0.
在使用根与系数的关系时,应注意:
⑴不是一般式的要先化成一般式;
⑵在使用x1+x2=-
时,注意“-”不要漏写.
归纳:
知识拓展
1.根与系数之间的关系在方程ax2+bx+c=0(a≠0)有根的前提下(b2-4ac≥0)才能够成立,运用根与系数的关系解题时首先要检验b2-4ac是否非负.
.
2.利用根与系数之间的关系可以不解方程而求出与根有关的代数式的值.比如
1.
x2-2x-15=0;
例1
口答下列方程的两根之和与两根之积.
2.
x2-6x+4=0;
3.
2x2+3x-5=0;
4.
3x2-7x=0;
5.
2x2=5.
x1+x2=
-p
,x1
·x2=q.
x1+x2=2,x1
·x2=-15.
x1+x2=6,x1
·x2=4.
ax2+bx+c=0(a≠0)
两边都
除以a
一元二次方程的根与系数的关系的应用
下列方程的两根和与两根积各是多少?
⑴
x2-3x+1=0
;
⑵
3x2-2x=2;
⑶
2x2+3x=0;
⑷
3x2=1
.
在使用根与系数的关系时:(1)不是一般式的要先化成一般式;(2)
在使用x1+x2=-
时,“-
”不要漏写.
注意
例2
已知方程5x2+kx-6=0的一个根是2,求它的另一个根及k的值.
解:设方程
5x2+kx-6=0的两个根分别是x1、x2,其中x1=2
.
所以:x1
·
x2=2x2=
即:x2=
由于x1+x2=2+
=
得:k=-7.
答:方程的另一个根是
,k=-7.
已知方程3x2-18x+m=0的一个根是1,求它的另一个根及m的值.
解:设方程
3x2-18x+m=0的两个根分别是x1、x2,其中x1=1.
所以:x1
+
x2=1+x2=6,
即:x2=5
.
由于x1·x2=1×5=
得:m=15.
答:方程的另一个根是5,m=15.
例3
不解方程,求方程2x2+3x-1=0的两根的平方和、倒数和.
解:根据根与系数的关系可知:
设x1,x2为方程x2-4x+1=0的两个根,则:
(1)x1+x2=
,
(2)x1·x2=
,
(3)
,
(4)
.
4
1
14
12
总结常见的求值:
求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和,两根之积的形式,再整体代入.
归纳
课堂小结
根与系数的关系
(韦达定理)
内
容
如果方程x2+px+q=0的两根是x1,x2,那么x1+x2=
-p
,x1
·x2=q.
如果一元二次方程
ax2+bx+c=0(a≠0)的两个根分别是x1、
x2,那么
应
用
常见变形
【课后练习】
1.一元二次方程x2-2x-3=0的根为(
)
A.x1=1,x2=3
B.x1=-1,x2=3
C.x1=-1,x2=-3
D.x1=1,x2=-3
2.已知关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=2,x2=4,则m+n的值是( )
A.﹣10
B.10
C.﹣6
D.2
3.已知m、n是方程x2+3x﹣2=0的两个实数根,则m2+4m+n+2mn的值为(
)
A.1
B.3
C.﹣5
D.﹣9
4.关于x的方程x2+mx+n=0的两根中只有一个等于0,则下列条件中正确的是(
)
A.m=0,n=0
B.m=0,n0
C.m0,n=0
D.m0,n0
5.已知关于x的一元二次方程x2-6x+k+1=0的两个实数根是x1,x2,且x21+x22=24,则k的值是().
A.8
B.-7
C.6
D.5
【课后练习】答案
1.B
2.D
3.C
4.C
5.D
【课后练习】
1.下列一元二次方程两实数根和为﹣4的是(
)
A.x2+2x﹣4=0
B.x2﹣4x+4=0
C.x2+4x+10=0
D.x2+4x﹣5=0
2.若关于x的一元二次方程x2﹣2x+m=0有一个解为x=﹣1,则另一个解为( )
A.1
B.﹣3
C.3
D.4
3.设a,b是方程x2+x-2009=0的两个实数根,则a2+2a+b的值为(
)
A.2006
B.2007
C.2008
D.2009
4.一元二次方程x2+kx﹣3=0的一个根是x=1,则另一个根是(
)
A.3
B.﹣1
C.﹣3
D.﹣2
5.已知x1,x2是一元二次方程的两根,则x1+x2的值是(
)
A.0
B.2
C.-2
D.4
6.方程
与
所有根的乘积等于(
)
A.-18
B.18
C.-3
D.3
7.定义:如果一元二次方程ax2+bx+c=0(a≠0)满足a+b+c=0,那么我们称这个方程为“和谐”方程;如果一元二次方程ax2+bx+c=0(a≠0)满足a﹣b+c=0那么我们称这个方程为“美好”方程,如果一个一元二次方程既是“和谐”方程又是“美好”方程,则下列结论正确的是( )
A.方有两个相等的实数根
B.方程有一根等于0
C.方程两根之和等于0
D.方程两根之积等于0
8.已知关于x的一元二次方程x2+2x+a﹣1=0有两根为x1和x2,且
x21-x1x2=0,则a的值是
A.a=1
B.a=1或a=﹣2
C.a=2
D.a=1或a=2
9.若
是一元二次方程
的两根,则(
)
A.-8
B.32
C.16
D.40
10.若a
b是方程
的两个实数根,则
(
)
A.2018
B.2017
C.2016
D.2015
11.已知一元二次方程x2-3x-2=0的两个实数根为x1,x2,则(x1-1)(x2-1)的值是______________.
12.已知x1
,
x2是关于x的一元二次方程x2﹣5x+a=0的两个实数根,且x12﹣x22=10,则a=____.
13.已知一元二次方程x2﹣4x﹣3=0的两根为m、n,则m2n+mn2=________.
14.设x1、x2是一元二次方程x2-mx-6=0的两个根,且x1+x2=1,则x1=______,x2=______.
15.若x1,x2是一元二次方程x2﹣2x﹣1=0的两个根,则x12﹣x1+x2的值为_____
【课后练习】答案
1.D
2.C
3.C
4.C
5.B
6.A
7.C
8.D
9.C
10.B
11.-4
12.
13.﹣12
14.﹣2
3
15.3
第二十一章
一元二次方程
21.2.4
一元二次方程的根与系数的关系
【学习目标】
1.掌握一元二次方程根与系数的关系(韦达定理);
2.掌握运用韦达定理求出方程的一根与方程中的未知系数,能求出与两根有关的一些代数式的值。
复习引入
1.一元二次方程的求根公式是什么?
2.方程的两根x1和x2与系数a,b,c还有其它关系吗?
【学习探究】
方程
的求根公式
,不仅表示可以由方程的系数a,b,c决定根的值,而且反应了根
与系数之间的联系.
新课引入
一元二次方程的根与系数的关系
算一算
解下列方程并完成填空:
(1)x2+3x-4=0;
(2)x2-5x+6=0;
(3)2x2+3x+1=0.
一元二次方程
两
根
关
系
x1
x2
x2+3x-4=0
x2-5x+6=0
2x2+3x+1=0
-4
1
2
3
-1
x1+x2=-3
x1
·
x2=-4
x1+x2=5
x1
·
x2=6
猜一猜
(1)若一元二次方程的两根为x1,x2,则有x-x1=0,且x-x2=0,那么方程(x-x1)(x-x2)=0(x1,x2为已知数)的两根是什么?将方程化为x2+px+q=0的形式,你能看出x1,x2与p,q之间的关系吗?
重要发现
如果方程x2+px+q=0的两根是x1,x2,那么x1+x2=
-p
,x1
·x2=q.
(x-x1)(x-x2)=0.
x2-(x1+x2)x+x1·x2=0,
x2+px+q=0,
x1+x2=
-p
,x1
·x2=q.
猜一猜
(2)如果一元二次方程
ax2+bx+c=0(a≠0)的两个根分别是x1、
x2,那么,你可以发现什么结论?
证一证:
一元二次方程的根与系数的关系
(韦达定理)
如果一元二次方程
ax2+bx+c=0(a≠0)的两个根分别是x1、
x2,那么
注意
满足上述关系的前提条件
b2-4ac≥0.
在使用根与系数的关系时,应注意:
⑴不是一般式的要先化成一般式;
⑵在使用x1+x2=-
时,注意“-”不要漏写.
归纳:
知识拓展
1.根与系数之间的关系在方程ax2+bx+c=0(a≠0)有根的前提下(b2-4ac≥0)才能够成立,运用根与系数的关系解题时首先要检验b2-4ac是否非负.
.
2.利用根与系数之间的关系可以不解方程而求出与根有关的代数式的值.比如
1.
x2-2x-15=0;
例1
口答下列方程的两根之和与两根之积.
2.
x2-6x+4=0;
3.
2x2+3x-5=0;
4.
3x2-7x=0;
5.
2x2=5.
x1+x2=
-p
,x1
·x2=q.
x1+x2=2,x1
·x2=-15.
x1+x2=6,x1
·x2=4.
ax2+bx+c=0(a≠0)
两边都
除以a
一元二次方程的根与系数的关系的应用
下列方程的两根和与两根积各是多少?
⑴
x2-3x+1=0
;
⑵
3x2-2x=2;
⑶
2x2+3x=0;
⑷
3x2=1
.
在使用根与系数的关系时:(1)不是一般式的要先化成一般式;(2)
在使用x1+x2=-
时,“-
”不要漏写.
注意
例2
已知方程5x2+kx-6=0的一个根是2,求它的另一个根及k的值.
解:设方程
5x2+kx-6=0的两个根分别是x1、x2,其中x1=2
.
所以:x1
·
x2=2x2=
即:x2=
由于x1+x2=2+
=
得:k=-7.
答:方程的另一个根是
,k=-7.
已知方程3x2-18x+m=0的一个根是1,求它的另一个根及m的值.
解:设方程
3x2-18x+m=0的两个根分别是x1、x2,其中x1=1.
所以:x1
+
x2=1+x2=6,
即:x2=5
.
由于x1·x2=1×5=
得:m=15.
答:方程的另一个根是5,m=15.
例3
不解方程,求方程2x2+3x-1=0的两根的平方和、倒数和.
解:根据根与系数的关系可知:
设x1,x2为方程x2-4x+1=0的两个根,则:
(1)x1+x2=
,
(2)x1·x2=
,
(3)
,
(4)
.
4
1
14
12
总结常见的求值:
求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和,两根之积的形式,再整体代入.
归纳
课堂小结
根与系数的关系
(韦达定理)
内
容
如果方程x2+px+q=0的两根是x1,x2,那么x1+x2=
-p
,x1
·x2=q.
如果一元二次方程
ax2+bx+c=0(a≠0)的两个根分别是x1、
x2,那么
应
用
常见变形
【课后练习】
1.一元二次方程x2-2x-3=0的根为(
)
A.x1=1,x2=3
B.x1=-1,x2=3
C.x1=-1,x2=-3
D.x1=1,x2=-3
2.已知关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=2,x2=4,则m+n的值是( )
A.﹣10
B.10
C.﹣6
D.2
3.已知m、n是方程x2+3x﹣2=0的两个实数根,则m2+4m+n+2mn的值为(
)
A.1
B.3
C.﹣5
D.﹣9
4.关于x的方程x2+mx+n=0的两根中只有一个等于0,则下列条件中正确的是(
)
A.m=0,n=0
B.m=0,n0
C.m0,n=0
D.m0,n0
5.已知关于x的一元二次方程x2-6x+k+1=0的两个实数根是x1,x2,且x21+x22=24,则k的值是().
A.8
B.-7
C.6
D.5
【课后练习】答案
1.B
2.D
3.C
4.C
5.D
【课后练习】
1.下列一元二次方程两实数根和为﹣4的是(
)
A.x2+2x﹣4=0
B.x2﹣4x+4=0
C.x2+4x+10=0
D.x2+4x﹣5=0
2.若关于x的一元二次方程x2﹣2x+m=0有一个解为x=﹣1,则另一个解为( )
A.1
B.﹣3
C.3
D.4
3.设a,b是方程x2+x-2009=0的两个实数根,则a2+2a+b的值为(
)
A.2006
B.2007
C.2008
D.2009
4.一元二次方程x2+kx﹣3=0的一个根是x=1,则另一个根是(
)
A.3
B.﹣1
C.﹣3
D.﹣2
5.已知x1,x2是一元二次方程的两根,则x1+x2的值是(
)
A.0
B.2
C.-2
D.4
6.方程
与
所有根的乘积等于(
)
A.-18
B.18
C.-3
D.3
7.定义:如果一元二次方程ax2+bx+c=0(a≠0)满足a+b+c=0,那么我们称这个方程为“和谐”方程;如果一元二次方程ax2+bx+c=0(a≠0)满足a﹣b+c=0那么我们称这个方程为“美好”方程,如果一个一元二次方程既是“和谐”方程又是“美好”方程,则下列结论正确的是( )
A.方有两个相等的实数根
B.方程有一根等于0
C.方程两根之和等于0
D.方程两根之积等于0
8.已知关于x的一元二次方程x2+2x+a﹣1=0有两根为x1和x2,且
x21-x1x2=0,则a的值是
A.a=1
B.a=1或a=﹣2
C.a=2
D.a=1或a=2
9.若
是一元二次方程
的两根,则(
)
A.-8
B.32
C.16
D.40
10.若a
b是方程
的两个实数根,则
(
)
A.2018
B.2017
C.2016
D.2015
11.已知一元二次方程x2-3x-2=0的两个实数根为x1,x2,则(x1-1)(x2-1)的值是______________.
12.已知x1
,
x2是关于x的一元二次方程x2﹣5x+a=0的两个实数根,且x12﹣x22=10,则a=____.
13.已知一元二次方程x2﹣4x﹣3=0的两根为m、n,则m2n+mn2=________.
14.设x1、x2是一元二次方程x2-mx-6=0的两个根,且x1+x2=1,则x1=______,x2=______.
15.若x1,x2是一元二次方程x2﹣2x﹣1=0的两个根,则x12﹣x1+x2的值为_____
【课后练习】答案
1.D
2.C
3.C
4.C
5.B
6.A
7.C
8.D
9.C
10.B
11.-4
12.
13.﹣12
14.﹣2
3
15.3
同课章节目录
