七年级数学期末复习 第5章 轴对称
图片预览








文档简介
(共48张PPT)
期末复习
专题一、轴对称的识别
知识要点:
1.轴反射、轴对称、轴对称图形的概念
(1)什么叫轴对称图形?
如果一个图形沿着一条直线折叠,直线两旁的图形能够
_________,那么这
个图形叫做轴对称
图形,这条直线叫对称轴。
互相重合
(2) 什么叫轴对称?
把一个图形沿着某条直线作轴反射能够和另一个图形________,那么就说这两个图形关于这条直线对称。也称这两个图形轴对称。这条直线叫对称轴。
重合
(3)什么叫轴反射?
把一个图形沿着某条直线翻折并将图形____________就叫把该图形关直线l做了轴反射。
复印下来
2、轴对称图形与轴对称有什么区别与联系?
区别:
轴对称是___个图形之间的对称关系,而轴对称图形是一个图形自身的________.?
联系:①沿对称轴折叠后都能_______.
②如果把轴对称的两个图形看作一个整体,那么它就是一个_________图形;若把轴对称图形沿对称轴分成的两部分看作两个图形,那么它们就关于对称轴_______.?
二
位置特性
重合
轴对称
轴对称
典型题例剖析
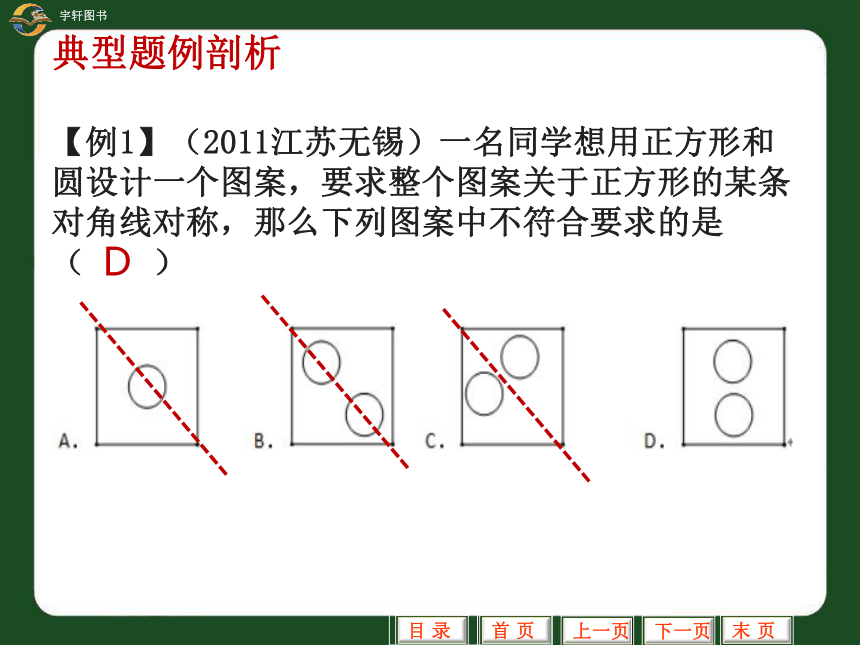
【例1】(2011江苏无锡)一名同学想用正方形和圆设计一个图案,要求整个图案关于正方形的某条对角线对称,那么下列图案中不符合要求的是
( )
D
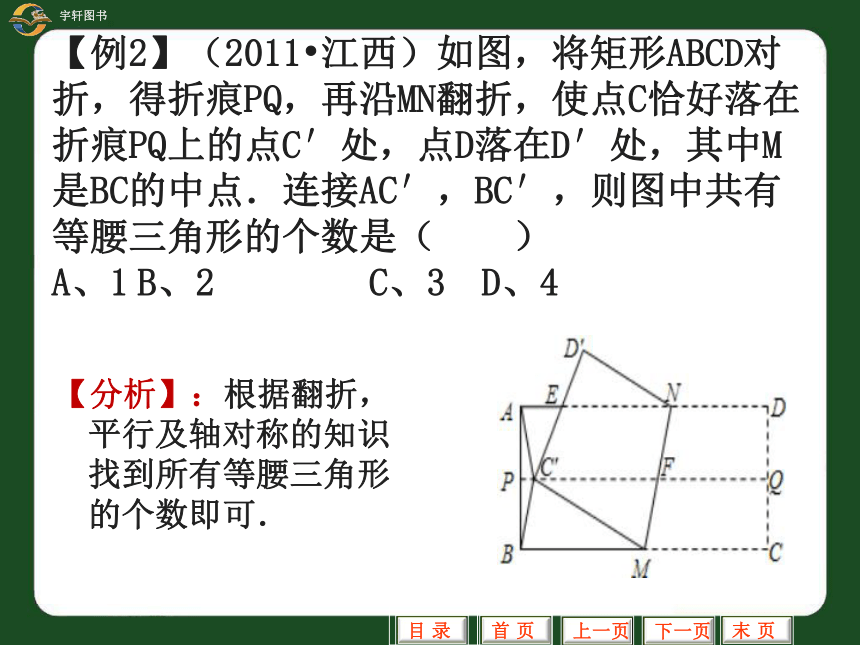
【例2】(2011 江西)如图,将矩形ABCD对折,得折痕PQ,再沿MN翻折,使点C恰好落在折痕PQ上的点C′处,点D落在D′处,其中M是BC的中点.连接AC′,BC′,则图中共有等腰三角形的个数是( )
A、1 B、2 C、3 D、4
【分析】:根据翻折,平行及轴对称的知识找到所有等腰三角形的个数即可.
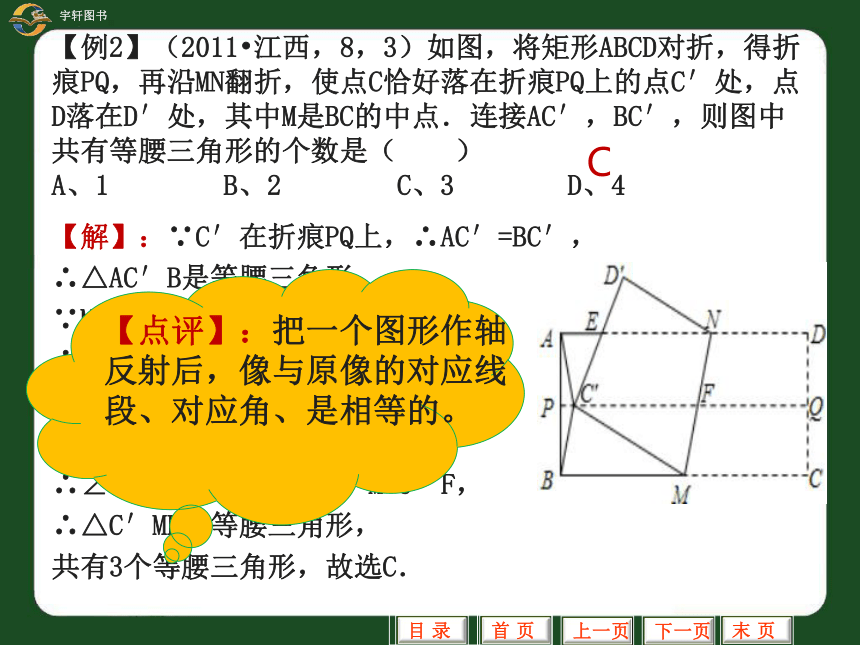
【例2】(2011 江西,8,3)如图,将矩形ABCD对折,得折痕PQ,再沿MN翻折,使点C恰好落在折痕PQ上的点C′处,点D落在D′处,其中M是BC的中点.连接AC′,BC′,则图中共有等腰三角形的个数是( )
A、1 B、2 C、3 D、4
【解】:∵C′在折痕PQ上,∴AC′=BC′,
∴△AC′B是等腰三角形;
∵M是BC的中点,∴BM=MC,
∴△BMC是等腰三角形;
由翻折可得∠CMF=∠C′MF,
∵PQ∥BC,∴∠PFM=∠CMF,
∴∠C′MF=∠PFM,∴C′M=C′F,
∴△C′MF是等腰三角形,
共有3个等腰三角形,故选C.
【点评】:把一个图形作轴
反射后,像与原像的对应线
段、对应角、是相等的。
C
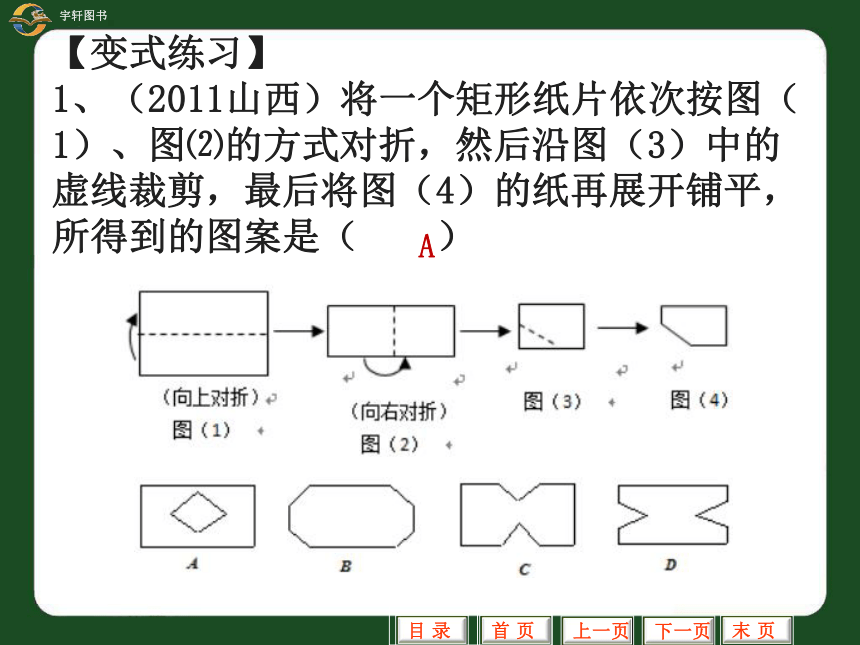
【变式练习】
1、(2011山西)将一个矩形纸片依次按图(1)、图⑵的方式对折,然后沿图(3)中的虚线裁剪,最后将图(4)的纸再展开铺平,所得到的图案是( )
A
2、下列四句话中的文字有三句具有对称规律,其中没有这种规律的一句是( )
A、上海自来水来自海上
B、有志者事竞成
C、清水池里池水清
D、蜜蜂酿蜂蜜
B
3、(2011重庆市)如图,在△ABC中,
∠ C=90 ° , 点D在AC上,将△BCD沿着直线BD翻折,使点C落在斜边AB上的点E处,DC=5cm,则点D到斜边AB的距离是 ________cm..
【解】:∵△BDE是△BDC
翻折而成,∠C=90°,
∴DE⊥AB,DE=CD,
∵DC=5cm,∴DE=5cm.
5
专题二 线段垂直平分线、角平分线
知识要点
1. 线段垂直平分线性质是什么?怎样判断一点在线段的垂直平分线上?
(1)线段垂直平分线是线
段的__________.
线段垂直平分线上的点到
这条线段两个端点的距离_______.
如图,若CD是AB的垂直平分线,P在CD上,则PA=PB
对称轴
相等
2、角平分线有哪些性质?
(1)角是轴对称图形,角平分线所在的直线是该角的______;
(2)角平分线上的点到这个角两边的距离________.
如图,OC平分∠AOB,P在OC上,PD ⊥OA,PE ⊥OB,D,E是垂足,则PD=PE
对称轴
相等
2. 怎样判断一个点在角的平分线上?
(1)定义判别法;
如图,若∠AOC=∠BOC,
则OC是∠AOB的平分线。
(2)性质判别法:在一个角的内部,
且到角的两边距离________的点,在
这个角的角平分线上.
如图,若,PD ⊥OA,PP
PE ⊥OB,PD=PE,则P OP平分∠AOB
相等
典型题例剖析
【例1】准备修建一个仓库P,使它到两条公路OA、OB的距离相等,且到两工厂A、B的距离也相等。请作出仓库P的位置。并说明理由。
【作法】1、作∠MON的平分线OC,
2、作线段AB的垂直平分线DE,交OC于P,
则P就是仓库的位置。
【分析】点P到OA、OB的距离相等,则P在∠MON的平分线上,点P到A、B的距离相等,则P在AB的垂直平分线上,因此P是∠MON的平分线与线段AB的垂直平分线的交点。
C
D
E
P
【例2】如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于
( )
A.6cm B.8cm C.10cm D.12cm
【解】∵DE垂直平分AB,∴AE=BE
∵BE+BC+EC=18,
∴AE+BC+EC=18cm,
即:AC+BC=18cm.
∵BC=8cm, ∴AC=18-8=10cm.
C
【例3】如图,OD平分∠EOF,分别在OE,OF上取点A,B,使OA=OB,点P在OD上,且PM⊥BD于点M,PN⊥AD于点N,求证:PM=PN.
【解】∵OD平分_______, OA=_____
∴△OBD与△OAD关于OD_______
∴∠ODB=∠________
∵PM⊥_____于点M,
PN⊥_______于点N
∴PM=_______
(_________________________________________)
【分析】由于PM⊥BD于点M,PN⊥AD于点N,因此要证明PM=PN,只需要证明PM=PN
∠EOF
OB
对称
∠ODA
DB
DA
PN
角平分线上的点到角的两边的距离相等。
【变式练习】
1、 如图,AB=AC=14cm,AB的垂直平分线交AB于点D,交AC于点E,如果BC=8cm,那么△EBC的周长是 ______
【解】∵DE垂直平分AB,
∴AE=BE
∴BE+BC+EC=AE+BC+EC
=AC+BC
=14+8
=22cm.
2、如图,已知AB∥CD, ∠BAC与∠ACD的平分线交于点O,OE垂直AC于E,且OE=2cm,则AB、CD的距离是______cm.
【解】过O点作FG⊥AB垂足为F,交CD于G.
∵AB∥CD, ∴FG⊥CD
∵OA平分∠BAC,OC平分∠ACD
∴OF=OE=OG=2cm,
∴FG=4cm.
即:AB、CD的距离是4cm.
F
G
3、.如图,已知∠ABC外部有两点M、N,试确定点P,使P到AB、BC的距离相等,且使PM=PN.
【作法】
1、作∠MON的垂直平分线OC,
2、作线段AB的垂直平分线DE,交OC于P,
则P就是就是要作的点。
C
E
D
P
专题三 三角形
【知识要点】
1.三角形的三边有什么关系?
(1)任何两边之和______第三边;
(2)任何两边之差_______第三边;
如图,△ABC中,a+b>c,b+c>a,c+a>b
若a>b>c,则a-c>b,a-b>c,b-c>a
大于
小于
2、知道三角形的两条边,第三条边的范围怎么确定?
其他两边_____<三角形的一边<其他两边______.
之差
之和
3.三角形的内角和是多少?外角和是多少?直角三角形的两个锐角有什么关系?
(1)三角形的内角和是______;
(2)三角形的外角和是______°;
(3)直角三角形的两个锐角______
如图, ∠ 1+∠2+ ∠ 3=180
∠4+ ∠ 5+∠6=360
△ABC中, ∠C=90 ,则∠ A+∠B=90
180 °
360 °
互余
4.三角形的内外角有何关系?
(1)三角形的一个内角与它相邻外角______
如图,∠1+∠ACB=180°
(2)三角形的一个外角等于它_________的两个内角的和;
如图, ∠1= ∠A+ ∠B
(3)三角形的一个外角大于
与它_______的任何一个内角。
如图, ∠1> ∠A, ∠1> ∠B
互补
不相邻
不相邻
5、三角形按角怎样分类?按边怎么分类?
不相等
直角
钝角
按角分
5、三角形按角怎样分类?按边怎么分类?
不相等
相等
相等
按边分
典型题例剖析
【例1】(2011内蒙古呼和浩特)如果等腰三角形两边长是6cm和3cm,那么它的周长是( )
A、9cm B、12cm
C、15cm或12cm D、15cm
【解】当6为腰,3为底时,6-3<6<6+3,能构成等腰三角形,
周长为5+5+3=13;
当3为腰,6为底时,3+3=6,不能构成三角形.故选D.
【分析】:由于两条边的长没有指明谁是腰、谁是底边,所以要分类讨论。
【点评】
求三角形的周长,不能盲目地将三边长相加起来,而应养成检验三边长能否组成三角形的好习惯,把不符合题意的舍去.
D
【例2】(2011年山东省东营市,5,3分)一副三角板如图叠放在一起,则图中∠α的度数为( )
A、75 B、60° C、65° D、55°
【解】:如图,∵∠1=45°,∠2=60°,
∴∠α=180°-45°-60°=75°.
故选A.
【分析】:因为三角板的度数为45°,60°,所以根据三角形内角和定理即可求解.
【点评】:充分利用三角板中角的度数的隐含条件和三角形内角和定理。
1
2
【变式练习】
1、(2011广西来宾)已知一个三角形的两边长分别是2和3,则下列数据中,可作为第三边长的是( )
A.1 B.3 C.5 D.7
【解】设这个三角形的第三边为x
根据三角形的三边关系定理,
得:3﹣2<x<3+2,
解得1<x<5.
故选B.
B
2、(2011年四川省绵阳市)将一副常规的三角尺按如图方式放置,则图中∠AOB的度数为( )
A、75° B、95°
C、105° D、120°
【解】∠ACO=45°-30°=15°
∴∠AOB=∠A+∠ACO=90°+15°=105°
故选C.
C
3.如图,在△ABC中, ∠C=68 ,∠B=42°,AD⊥BC于D,AE平分∠BAC,求∠EAD的度数
【证明】:
∵∠BAC=180 -(∠B+∠C)
=180 -(42°+68 )=70
∵AE平分∠BAC,∴∠BAE=0.5∠BAC=0.5×70°=35°
∵AD⊥BC,
∴∠BAD=90°-∠B=90°-42 =48
∴∠DAE=∠BAD-∠BAE=48°-35°=13
专题四、等腰三角形的性质和判定
知识要点:
1.等腰三角形有哪些性质?
(1)等腰三角形的两个______相等(简称:等边对等角)
如图,若AB=AC,则∠ B=∠C
(2)等腰三角形关于底边的垂直平分线________,从而它是_______图形.
底角
对称
轴对称
知识要点:
1.等腰三角形有哪些性质?
(3)等腰三角形的顶角平分线、底边上的高线、底边上的中线互相______(简称 “三线合一”).
如图,若AB=AC,BD=DC,
则 AD⊥BC, ∠BAD=∠CAD
若AB=AC,∠BAD=∠CAD,
则BD=DC, AD ⊥BC
若AB=AC,AD⊥BC,
则BD=DC, ∠BAD=∠CAD
重合
2. 等腰三角形有哪些常用的判定方法
等腰三角形的判定方法:
(1)根据定义,有两条边_____的三角形是等腰三角形;
如图,若AB=AC,则∠B= ∠C
(2)有两个角______的三角形是
等腰三角形(简称:等角对等边)
如图,若∠B= ∠C,则AB=AC
相等
相等
3.等边三角形有什么性质?
(1 )等边三角形三边都_____,三个角都____,且每个内角都等于______°.
(2).每条边上都具有“三线合一”的性质.
(3).是_______图形,有____条对称轴.
相等
相等
60
轴对称
三
4、怎样判定一个三角形是等边三角形?
(1)根据定义:______相等的三角形是等边三角形;
(2)三个角都________的三角形是等边三角形.
(3)有一个角等于_______度的等腰三角形是等边三角形。
三条边
相等
60
典型题例剖析
【例1】(2010河南)如图,在△ABC中,AB=AC,CD平分∠ACB,∠A=36°,则∠BDC的度数为 .
【解】:∵AB=AC,CD平分∠ACB,∠A=36°,
∴∠B=(180°﹣36°)÷2
=72°∠DCB=36°.
∴∠BDC=72°.
72°
【分析】:由AB=AC,CD平分∠ACB,∠A=36°,根据三角形内角和180°可求得∠B等于∠ACB,并能求出其角度,在△DBC求得所求角度.
【点评】:本题考查了等腰三角形
的性质,本题根据三角形内角和等
于180度,在△CDB中从而求得
∠BDC的角度.
【例2】(2011江苏扬州)已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC,
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由。
【分析】:(1)由OB=OC,即可求得∠OBC=∠OCB,利用等角的余角相等可以证得:∠ABC=∠ACB.
(2)由OB=OC,得O在BC的垂直平分线上,而BC的垂直平分线与∠A的平分线所在直线重合。
【例2】(2011江苏扬州)已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC,
(1)求证:△ABC是等腰三角形;
【解】:(1)∵OB=OC∴∠OBC=∠OCB,
∵∠BEC=∠BDC=90°,
∴∠ABC+∠BCE=90
∠DBC+∠ACB=90°,
∴∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形;
等。
【例2】(2011江苏扬州)已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC,
(2)判断点O是否在∠BAC的角平分线上,并说明理由。
【解】(2)连接AO并延长交BC于F
∵AB=AC,OB=OC,
∴AE是BC的垂直平分线,
∴∠BAF=∠CAF,
∴点O在∠BAC的角平分线上.
【点评】:判断一个三角形是等腰是三角形,可以判断它有两条边相等,也可以判断它有两个角相
F
【例3】如图,△ABC是等边三角形,P为△ABC内部一点,将△ABP绕点A逆时针旋转后,能与 △ACPˊ重合,如果AP=3,求PPˊ的长.
【解】:因为△ABC是等边三角形,
所以∠BAC=60°.
由旋转得到AP=A Pˊ,∠BAP=∠CA Pˊ.
所以∠PA Pˊ=∠BAC=60°.
所以∠PA Pˊ=∠A PˊP
=∠AP Pˊ=60°.
所以△A PPˊ是等边三角形.
所以PPˊ=AP=3.
【分析】:欲求PPˊ的长,结合旋转的特点,说明△A PPˊ是等边三角形.
【点评】:将条件为转在恰当的等边形中是解决本题的关键.
【变式训练】
1、(2010福建泉州)如图,在△ABC中,AB=AC,∠B=40°,则∠A= ____.
【解】:∵AB=AC,
∴∠B=∠C=40°
∴∠A=180°﹣40°﹣40°
=100°.
100°
【变式训练】
2、如图,在△ABC中,AB=AC,点D为BC边的中点,∠BAD=20°,则∠C=_____.
【解】:∵AB=CA,
∴△ABC是等腰三角形,
∵D是BC边上的中点,
∴AD平分∠BAC,
∵∠BAD=20°.
∴∠C=90°﹣20°=70°.
70°
3.如图,△ABC是等边三角形,P为△ABC内部一点,将△ABP绕点A逆时针旋转后,
能与△ACPˊ重合,如果∠BAP=30°,那么AC与PPˊ有何位置关系?
【解】:∵△ABC是等边三角形
∴∠BAC=60°.
由旋转得到:
AP=A Pˊ,∠BAP=∠CA Pˊ.
∴∠PA Pˊ=∠BAC=60°.
∴∠PA Pˊ=∠A PˊP=∠AP Pˊ=60°.
∴△A PPˊ是等边三角形.
又∵∠CA Pˊ=∠BAP=30°,∴AC⊥PPˊ.
作业:数学报《轴对称》综合测试题
期末复习
专题一、轴对称的识别
知识要点:
1.轴反射、轴对称、轴对称图形的概念
(1)什么叫轴对称图形?
如果一个图形沿着一条直线折叠,直线两旁的图形能够
_________,那么这
个图形叫做轴对称
图形,这条直线叫对称轴。
互相重合
(2) 什么叫轴对称?
把一个图形沿着某条直线作轴反射能够和另一个图形________,那么就说这两个图形关于这条直线对称。也称这两个图形轴对称。这条直线叫对称轴。
重合
(3)什么叫轴反射?
把一个图形沿着某条直线翻折并将图形____________就叫把该图形关直线l做了轴反射。
复印下来
2、轴对称图形与轴对称有什么区别与联系?
区别:
轴对称是___个图形之间的对称关系,而轴对称图形是一个图形自身的________.?
联系:①沿对称轴折叠后都能_______.
②如果把轴对称的两个图形看作一个整体,那么它就是一个_________图形;若把轴对称图形沿对称轴分成的两部分看作两个图形,那么它们就关于对称轴_______.?
二
位置特性
重合
轴对称
轴对称
典型题例剖析
【例1】(2011江苏无锡)一名同学想用正方形和圆设计一个图案,要求整个图案关于正方形的某条对角线对称,那么下列图案中不符合要求的是
( )
D
【例2】(2011 江西)如图,将矩形ABCD对折,得折痕PQ,再沿MN翻折,使点C恰好落在折痕PQ上的点C′处,点D落在D′处,其中M是BC的中点.连接AC′,BC′,则图中共有等腰三角形的个数是( )
A、1 B、2 C、3 D、4
【分析】:根据翻折,平行及轴对称的知识找到所有等腰三角形的个数即可.
【例2】(2011 江西,8,3)如图,将矩形ABCD对折,得折痕PQ,再沿MN翻折,使点C恰好落在折痕PQ上的点C′处,点D落在D′处,其中M是BC的中点.连接AC′,BC′,则图中共有等腰三角形的个数是( )
A、1 B、2 C、3 D、4
【解】:∵C′在折痕PQ上,∴AC′=BC′,
∴△AC′B是等腰三角形;
∵M是BC的中点,∴BM=MC,
∴△BMC是等腰三角形;
由翻折可得∠CMF=∠C′MF,
∵PQ∥BC,∴∠PFM=∠CMF,
∴∠C′MF=∠PFM,∴C′M=C′F,
∴△C′MF是等腰三角形,
共有3个等腰三角形,故选C.
【点评】:把一个图形作轴
反射后,像与原像的对应线
段、对应角、是相等的。
C
【变式练习】
1、(2011山西)将一个矩形纸片依次按图(1)、图⑵的方式对折,然后沿图(3)中的虚线裁剪,最后将图(4)的纸再展开铺平,所得到的图案是( )
A
2、下列四句话中的文字有三句具有对称规律,其中没有这种规律的一句是( )
A、上海自来水来自海上
B、有志者事竞成
C、清水池里池水清
D、蜜蜂酿蜂蜜
B
3、(2011重庆市)如图,在△ABC中,
∠ C=90 ° , 点D在AC上,将△BCD沿着直线BD翻折,使点C落在斜边AB上的点E处,DC=5cm,则点D到斜边AB的距离是 ________cm..
【解】:∵△BDE是△BDC
翻折而成,∠C=90°,
∴DE⊥AB,DE=CD,
∵DC=5cm,∴DE=5cm.
5
专题二 线段垂直平分线、角平分线
知识要点
1. 线段垂直平分线性质是什么?怎样判断一点在线段的垂直平分线上?
(1)线段垂直平分线是线
段的__________.
线段垂直平分线上的点到
这条线段两个端点的距离_______.
如图,若CD是AB的垂直平分线,P在CD上,则PA=PB
对称轴
相等
2、角平分线有哪些性质?
(1)角是轴对称图形,角平分线所在的直线是该角的______;
(2)角平分线上的点到这个角两边的距离________.
如图,OC平分∠AOB,P在OC上,PD ⊥OA,PE ⊥OB,D,E是垂足,则PD=PE
对称轴
相等
2. 怎样判断一个点在角的平分线上?
(1)定义判别法;
如图,若∠AOC=∠BOC,
则OC是∠AOB的平分线。
(2)性质判别法:在一个角的内部,
且到角的两边距离________的点,在
这个角的角平分线上.
如图,若,PD ⊥OA,PP
PE ⊥OB,PD=PE,则P OP平分∠AOB
相等
典型题例剖析
【例1】准备修建一个仓库P,使它到两条公路OA、OB的距离相等,且到两工厂A、B的距离也相等。请作出仓库P的位置。并说明理由。
【作法】1、作∠MON的平分线OC,
2、作线段AB的垂直平分线DE,交OC于P,
则P就是仓库的位置。
【分析】点P到OA、OB的距离相等,则P在∠MON的平分线上,点P到A、B的距离相等,则P在AB的垂直平分线上,因此P是∠MON的平分线与线段AB的垂直平分线的交点。
C
D
E
P
【例2】如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于
( )
A.6cm B.8cm C.10cm D.12cm
【解】∵DE垂直平分AB,∴AE=BE
∵BE+BC+EC=18,
∴AE+BC+EC=18cm,
即:AC+BC=18cm.
∵BC=8cm, ∴AC=18-8=10cm.
C
【例3】如图,OD平分∠EOF,分别在OE,OF上取点A,B,使OA=OB,点P在OD上,且PM⊥BD于点M,PN⊥AD于点N,求证:PM=PN.
【解】∵OD平分_______, OA=_____
∴△OBD与△OAD关于OD_______
∴∠ODB=∠________
∵PM⊥_____于点M,
PN⊥_______于点N
∴PM=_______
(_________________________________________)
【分析】由于PM⊥BD于点M,PN⊥AD于点N,因此要证明PM=PN,只需要证明PM=PN
∠EOF
OB
对称
∠ODA
DB
DA
PN
角平分线上的点到角的两边的距离相等。
【变式练习】
1、 如图,AB=AC=14cm,AB的垂直平分线交AB于点D,交AC于点E,如果BC=8cm,那么△EBC的周长是 ______
【解】∵DE垂直平分AB,
∴AE=BE
∴BE+BC+EC=AE+BC+EC
=AC+BC
=14+8
=22cm.
2、如图,已知AB∥CD, ∠BAC与∠ACD的平分线交于点O,OE垂直AC于E,且OE=2cm,则AB、CD的距离是______cm.
【解】过O点作FG⊥AB垂足为F,交CD于G.
∵AB∥CD, ∴FG⊥CD
∵OA平分∠BAC,OC平分∠ACD
∴OF=OE=OG=2cm,
∴FG=4cm.
即:AB、CD的距离是4cm.
F
G
3、.如图,已知∠ABC外部有两点M、N,试确定点P,使P到AB、BC的距离相等,且使PM=PN.
【作法】
1、作∠MON的垂直平分线OC,
2、作线段AB的垂直平分线DE,交OC于P,
则P就是就是要作的点。
C
E
D
P
专题三 三角形
【知识要点】
1.三角形的三边有什么关系?
(1)任何两边之和______第三边;
(2)任何两边之差_______第三边;
如图,△ABC中,a+b>c,b+c>a,c+a>b
若a>b>c,则a-c>b,a-b>c,b-c>a
大于
小于
2、知道三角形的两条边,第三条边的范围怎么确定?
其他两边_____<三角形的一边<其他两边______.
之差
之和
3.三角形的内角和是多少?外角和是多少?直角三角形的两个锐角有什么关系?
(1)三角形的内角和是______;
(2)三角形的外角和是______°;
(3)直角三角形的两个锐角______
如图, ∠ 1+∠2+ ∠ 3=180
∠4+ ∠ 5+∠6=360
△ABC中, ∠C=90 ,则∠ A+∠B=90
180 °
360 °
互余
4.三角形的内外角有何关系?
(1)三角形的一个内角与它相邻外角______
如图,∠1+∠ACB=180°
(2)三角形的一个外角等于它_________的两个内角的和;
如图, ∠1= ∠A+ ∠B
(3)三角形的一个外角大于
与它_______的任何一个内角。
如图, ∠1> ∠A, ∠1> ∠B
互补
不相邻
不相邻
5、三角形按角怎样分类?按边怎么分类?
不相等
直角
钝角
按角分
5、三角形按角怎样分类?按边怎么分类?
不相等
相等
相等
按边分
典型题例剖析
【例1】(2011内蒙古呼和浩特)如果等腰三角形两边长是6cm和3cm,那么它的周长是( )
A、9cm B、12cm
C、15cm或12cm D、15cm
【解】当6为腰,3为底时,6-3<6<6+3,能构成等腰三角形,
周长为5+5+3=13;
当3为腰,6为底时,3+3=6,不能构成三角形.故选D.
【分析】:由于两条边的长没有指明谁是腰、谁是底边,所以要分类讨论。
【点评】
求三角形的周长,不能盲目地将三边长相加起来,而应养成检验三边长能否组成三角形的好习惯,把不符合题意的舍去.
D
【例2】(2011年山东省东营市,5,3分)一副三角板如图叠放在一起,则图中∠α的度数为( )
A、75 B、60° C、65° D、55°
【解】:如图,∵∠1=45°,∠2=60°,
∴∠α=180°-45°-60°=75°.
故选A.
【分析】:因为三角板的度数为45°,60°,所以根据三角形内角和定理即可求解.
【点评】:充分利用三角板中角的度数的隐含条件和三角形内角和定理。
1
2
【变式练习】
1、(2011广西来宾)已知一个三角形的两边长分别是2和3,则下列数据中,可作为第三边长的是( )
A.1 B.3 C.5 D.7
【解】设这个三角形的第三边为x
根据三角形的三边关系定理,
得:3﹣2<x<3+2,
解得1<x<5.
故选B.
B
2、(2011年四川省绵阳市)将一副常规的三角尺按如图方式放置,则图中∠AOB的度数为( )
A、75° B、95°
C、105° D、120°
【解】∠ACO=45°-30°=15°
∴∠AOB=∠A+∠ACO=90°+15°=105°
故选C.
C
3.如图,在△ABC中, ∠C=68 ,∠B=42°,AD⊥BC于D,AE平分∠BAC,求∠EAD的度数
【证明】:
∵∠BAC=180 -(∠B+∠C)
=180 -(42°+68 )=70
∵AE平分∠BAC,∴∠BAE=0.5∠BAC=0.5×70°=35°
∵AD⊥BC,
∴∠BAD=90°-∠B=90°-42 =48
∴∠DAE=∠BAD-∠BAE=48°-35°=13
专题四、等腰三角形的性质和判定
知识要点:
1.等腰三角形有哪些性质?
(1)等腰三角形的两个______相等(简称:等边对等角)
如图,若AB=AC,则∠ B=∠C
(2)等腰三角形关于底边的垂直平分线________,从而它是_______图形.
底角
对称
轴对称
知识要点:
1.等腰三角形有哪些性质?
(3)等腰三角形的顶角平分线、底边上的高线、底边上的中线互相______(简称 “三线合一”).
如图,若AB=AC,BD=DC,
则 AD⊥BC, ∠BAD=∠CAD
若AB=AC,∠BAD=∠CAD,
则BD=DC, AD ⊥BC
若AB=AC,AD⊥BC,
则BD=DC, ∠BAD=∠CAD
重合
2. 等腰三角形有哪些常用的判定方法
等腰三角形的判定方法:
(1)根据定义,有两条边_____的三角形是等腰三角形;
如图,若AB=AC,则∠B= ∠C
(2)有两个角______的三角形是
等腰三角形(简称:等角对等边)
如图,若∠B= ∠C,则AB=AC
相等
相等
3.等边三角形有什么性质?
(1 )等边三角形三边都_____,三个角都____,且每个内角都等于______°.
(2).每条边上都具有“三线合一”的性质.
(3).是_______图形,有____条对称轴.
相等
相等
60
轴对称
三
4、怎样判定一个三角形是等边三角形?
(1)根据定义:______相等的三角形是等边三角形;
(2)三个角都________的三角形是等边三角形.
(3)有一个角等于_______度的等腰三角形是等边三角形。
三条边
相等
60
典型题例剖析
【例1】(2010河南)如图,在△ABC中,AB=AC,CD平分∠ACB,∠A=36°,则∠BDC的度数为 .
【解】:∵AB=AC,CD平分∠ACB,∠A=36°,
∴∠B=(180°﹣36°)÷2
=72°∠DCB=36°.
∴∠BDC=72°.
72°
【分析】:由AB=AC,CD平分∠ACB,∠A=36°,根据三角形内角和180°可求得∠B等于∠ACB,并能求出其角度,在△DBC求得所求角度.
【点评】:本题考查了等腰三角形
的性质,本题根据三角形内角和等
于180度,在△CDB中从而求得
∠BDC的角度.
【例2】(2011江苏扬州)已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC,
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由。
【分析】:(1)由OB=OC,即可求得∠OBC=∠OCB,利用等角的余角相等可以证得:∠ABC=∠ACB.
(2)由OB=OC,得O在BC的垂直平分线上,而BC的垂直平分线与∠A的平分线所在直线重合。
【例2】(2011江苏扬州)已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC,
(1)求证:△ABC是等腰三角形;
【解】:(1)∵OB=OC∴∠OBC=∠OCB,
∵∠BEC=∠BDC=90°,
∴∠ABC+∠BCE=90
∠DBC+∠ACB=90°,
∴∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形;
等。
【例2】(2011江苏扬州)已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC,
(2)判断点O是否在∠BAC的角平分线上,并说明理由。
【解】(2)连接AO并延长交BC于F
∵AB=AC,OB=OC,
∴AE是BC的垂直平分线,
∴∠BAF=∠CAF,
∴点O在∠BAC的角平分线上.
【点评】:判断一个三角形是等腰是三角形,可以判断它有两条边相等,也可以判断它有两个角相
F
【例3】如图,△ABC是等边三角形,P为△ABC内部一点,将△ABP绕点A逆时针旋转后,能与 △ACPˊ重合,如果AP=3,求PPˊ的长.
【解】:因为△ABC是等边三角形,
所以∠BAC=60°.
由旋转得到AP=A Pˊ,∠BAP=∠CA Pˊ.
所以∠PA Pˊ=∠BAC=60°.
所以∠PA Pˊ=∠A PˊP
=∠AP Pˊ=60°.
所以△A PPˊ是等边三角形.
所以PPˊ=AP=3.
【分析】:欲求PPˊ的长,结合旋转的特点,说明△A PPˊ是等边三角形.
【点评】:将条件为转在恰当的等边形中是解决本题的关键.
【变式训练】
1、(2010福建泉州)如图,在△ABC中,AB=AC,∠B=40°,则∠A= ____.
【解】:∵AB=AC,
∴∠B=∠C=40°
∴∠A=180°﹣40°﹣40°
=100°.
100°
【变式训练】
2、如图,在△ABC中,AB=AC,点D为BC边的中点,∠BAD=20°,则∠C=_____.
【解】:∵AB=CA,
∴△ABC是等腰三角形,
∵D是BC边上的中点,
∴AD平分∠BAC,
∵∠BAD=20°.
∴∠C=90°﹣20°=70°.
70°
3.如图,△ABC是等边三角形,P为△ABC内部一点,将△ABP绕点A逆时针旋转后,
能与△ACPˊ重合,如果∠BAP=30°,那么AC与PPˊ有何位置关系?
【解】:∵△ABC是等边三角形
∴∠BAC=60°.
由旋转得到:
AP=A Pˊ,∠BAP=∠CA Pˊ.
∴∠PA Pˊ=∠BAC=60°.
∴∠PA Pˊ=∠A PˊP=∠AP Pˊ=60°.
∴△A PPˊ是等边三角形.
又∵∠CA Pˊ=∠BAP=30°,∴AC⊥PPˊ.
作业:数学报《轴对称》综合测试题
