11.2与三角形有关的角同步能力提升训练-2021-2022学年度人教版八年级数学上册(Word版含答案)
文档属性
| 名称 | 11.2与三角形有关的角同步能力提升训练-2021-2022学年度人教版八年级数学上册(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 148.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 09:32:00 | ||
图片预览




文档简介
2021-2022学年人教版八年级数学上册《11.2与三角形有关的角》
同步能力提升训练(附答案)
1.在一个直角三角形中,一个锐角等于54°,则另一个锐角的度数是( )
A.26°
B.36°
C.45°
D.56°
2.已知在Rt△ABC中,∠B=90°,∠C=35°,则∠A等于( )
A.35°
B.45°
C.55°
D.65°
3.一个三角形其中一个外角的补角等于与它不相邻的两个内角的差,则这个三角形一定是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
4.将一副三角尺按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.45°
B.65°
C.75°
D.85°
5.已知△ABC中,∠A:∠B:∠C=3:4:7,则△ABC一定是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
6.如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=48°,∠C=68°,则∠DAE的度数是( )
A.10°
B.12°
C.14°
D.16°
7.在△ABC中,∠A:∠B:∠C=1:1:4,则∠A=( )
A.30°
B.45°
C.90°
D.120°
8.如图,∠CBA=∠ACB=65°,∠ACE=15°,则∠AEC的度数是( )
A.35°
B.50°
C.65°
D.80°
9.如图,△ABC中,∠A=65°,∠B=50°,点D在BC延长线上,则∠ACD的度数是( )
A.65°
B.105°
C.115°
D.125°
10.如图,∠BCD是△ABC的一个外角,E是边AB上一点.下列结论不正确的是( )
A.∠BCD>∠A
B.∠BCD>∠1
C.∠2>∠3
D.∠BCD=∠A+∠B
11.已知AH为△ABC的高,若∠B=40°,∠ACH=65°,则∠BAC的度数为
°.
12.如图,∠ABD=15°,∠ACD=30°,∠A=45°,则∠BDC的度数为
°.
13.如图,一般轮船按箭头所示方向行驶,C处有一灯塔,当轮船从A点行驶到B点时,∠ACB=
°.
14.如图,CE是△ABC的外角∠ACD的平分线,CE交BA的延长线于点E,∠B=35°,∠E=25°,则∠ACD的度数为
.
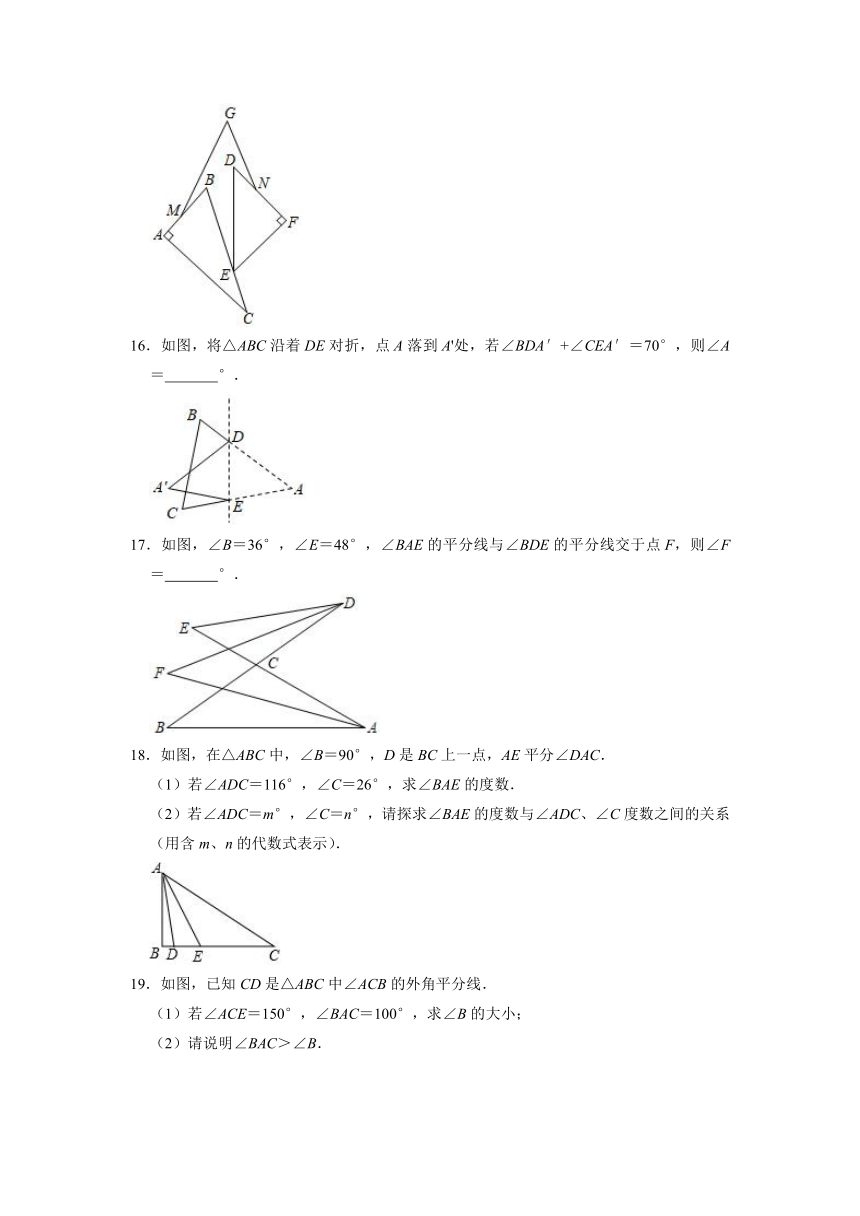
15.将一副三角板如图放置,其中∠C=30°,∠D=45°,点E在BC边上,M,N分别为AB,DF上的点,G为三角板外一点,连接GM,GN,若∠G=50°,则∠GMB+∠BED+∠DNG=
.
16.如图,将△ABC沿着DE对折,点A落到A'处,若∠BDA′+∠CEA′=70°,则∠A=
°.
17.如图,∠B=36°,∠E=48°,∠BAE的平分线与∠BDE的平分线交于点F,则∠F=
°.
18.如图,在△ABC中,∠B=90°,D是BC上一点,AE平分∠DAC.
(1)若∠ADC=116°,∠C=26°,求∠BAE的度数.
(2)若∠ADC=m°,∠C=n°,请探求∠BAE的度数与∠ADC、∠C度数之间的关系(用含m、n的代数式表示).
19.如图,已知CD是△ABC中∠ACB的外角平分线.
(1)若∠ACE=150°,∠BAC=100°,求∠B的大小;
(2)请说明∠BAC>∠B.
20.如图,AD、AE分别是△ABC的高和角平分线,∠B=40°,∠ACB=80°.点F在BC的延长线上,FG⊥AE,垂足为H,FG与AB相交于点G.
(1)求∠AGF的度数;
(2)求∠EAD的度数.
参考答案
1.解:在一个直角三角形中,一个锐角等于54°,
∴另一个锐角的度数是:90°﹣54°=36°.
故选:B.
2.解:在Rt△ABC中,∠B=90°,∠C=35°,
则∠A=90°﹣35°=55°,
故选:C.
3.解:由题意得:这个三角形的一个内角等于与它不相邻的两个内角的差.
设这个内角为∠1,另外两个内角为∠2、∠3且∠1=∠2﹣∠3.
∵180°﹣∠1=∠2+∠3,
∴2∠2=180°.
∴∠2=90°.
∴这个三角形的是直角三角形.
故选:B.
4.解:∵∠2+60°+45°=180°,
∴∠2=75°.
∵直尺的上下两边平行,
∴∠1=∠2=75°.
故选:C.
5.解:由题意可设∠A=3x,∠B=4x,∠C=7x.
∵∠A+∠B+∠C=180°,
∴3x+4x+7x=180°.
∴x=()°.
∴7x=90°.
∴△ABC是直角三角形.
故选:B.
6.解:∵∠B=48°,∠C=68°,
∴∠BAC=180°﹣∠B﹣∠C=64°,
∵AE平分∠BAC,
∴∠EAC=BAC=32°,
∵AD是△ABC的BC边上的高,
∴∠ADC=90°,
∵∠C=68°,
∴∠DAC=90°﹣∠C=22°,
∴∠DAE=∠EAC﹣∠DAC=32°﹣22°=10°,
故选:A.
7.解:∵∠A:∠B:∠C=1:1:4且∠A+∠B+∠C=180°,
∴∠A==30°.
故选:A.
8.解:∵∠CBA=∠ACB=65°,
∴∠BAC=180°﹣∠CBA﹣∠ACB=180°﹣65°﹣65°=50°,
∴∠EAC=130°,
∵∠ACE=15°,
∴∠AEC=35°,
故选:A.
9.解:∵∠ACD是△ABC的外角,
∴∠ACD=∠A+∠B=65°+50°=115°.
故选:C.
10.解:A、∠BCD是△ABC的一个外角,则∠BCD>∠A,不符合题意.
B、∠BCD是△ABC的一个外角,则∠1是△BEC的一个外角,∠BCD与∠1无法比较大小,符合题意.
C、∠2是△AEC的一个外角,则∠2>∠3,不符合题意.
D、∠BCD是△ABC的一个外角,则∠BCD=∠A+∠B,不符合题意.
故选:B.
11.解:如图,当△ABC是钝角三角形时,
∵∠B=40°,∠ACH=65°,∠ACH=∠BAC+∠B,
∴∠BAC=∠ACH﹣∠B=65°﹣40°=25°;
如图,当△ABC是锐角三角形时,
∵∠B=40°,∠ACH=65°,∠BAC+∠ACH+∠B=180°,
∴∠BAC=180°﹣∠ACH﹣∠B=180°﹣65°﹣40°=75°.
故答案为:25或75.
12.解:延长BD交AC于点E,
∵∠CEB=∠A+∠ABD,∠BDC=∠CEB+∠ACD,
∴∠BDC=∠A+∠ABD+∠ACD,
∵∠ABD=15°,∠ACD=30°,∠A=45°,
∴∠BDC=45°+30°+15°=90°,
故答案为90.
13.解:∵∠CBD=∠A+∠C,
∴∠C=∠CBD﹣∠A
=70°﹣30°
=40°,
故答案为:40.
14.解:∵∠ECD是△BCE的外角,∠B=35°,∠E=25°,
∴∠ECD=∠B+∠E=35°+25°=60°,
∵CE是∠ACD的平分线,
∴∠ACD=2∠ECD=120°,
故答案为:120°.
15.解:∵∠C=30°,∠D=45°,
∴∠B=180°﹣∠A﹣∠C=180°﹣90°﹣30°=60°,
延长FD交MG于P点,延长AB交FP于Q点,
∴∠QBE=180°﹣∠ABC=180°﹣60°=120°,
∴∠QDE==180°﹣∠FDE=180°﹣45°=135°,
∵∠FPM=∠DNG+∠G=∠DNG+50°,
∴∠BQD=∠GMB+∠FPM=GMB+∠DNG+50°,
∠BQD+∠QDE+BED+∠QBE=360°,
∴∠GMB+∠DNG+50°+135°+∠BED+120°=360°
∴∠GMB+∠BED+∠DNG=55°,
故答案为:55°.
16.解:∵将△ABC沿着DE对折,点A落到A'处,
∴∠EDA′=∠EDA,∠DEA′=∠DEA,
∵∠BDA′+2∠EDA=180°,∠CEA′+2∠DEA=180°,
∴∠BDA′+2∠EDA+∠CEA′+2∠DEA=360°,
∵∠BDA′+∠CEA′=70°,
∴∠EDA+∠DEA=145°,
∴∠A=35°,
故答案为:35.
17.解:如图,
∵∠BAE的平分线与∠BDE的平分线交于点F,
∴∠BAM=∠FAC=∠BAC,∠EDF=∠CDF=∠EDC,
∵∠BMF=∠F+∠CDF,∠BMF=∠B+∠BAF,
∴∠F+∠CDF=∠B+∠BAF,
∴∠F=∠B+∠BAF﹣∠CDF
=∠B+∠BAC﹣∠EDC
=∠B+(∠BAC﹣∠EDC)
∵∠ECB=∠E+∠EDC=∠B+∠BAC,
∴∠BAC﹣∠EDC=∠E﹣∠B,
∴∠F=∠B+(∠E﹣∠B)
=∠E+∠B
=(∠E+∠B)
=(48°+36°)
=42°,
故答案为:42.
18.解:(1)∵∠B=90°,∠C=26°,
∴∠BAC=64°,
∵∠ADC=116°,
∴∠BAD=26°,
∴∠DAC=64°﹣26°=38°,
∵AE是∠DAC的角平分线,
∴∠DAE=19°,
∴∠BAE=∠BAD+∠DAE=26°+19°=45°;
(2)∵∠B=90°,∠C=n°,
∴∠BAC=90°﹣n°,
∵∠ADC=m°,
∴∠BAD=m°﹣90°,
∴∠DAC=∠BAC﹣∠BAD=(90°﹣n°)﹣(m°﹣90°),
∵AE是∠DAC的角平分线,
∴∠DAE=DAC=(180°﹣n°﹣m°),
∴∠BAE=∠BAD+∠DAE=m°﹣90°+(180°﹣n°﹣m°)=m°﹣n°.
19.解:(1)∵∠ACE=150°,∠BAC=100°,
∴∠B=∠ACE﹣∠BAC=150°﹣100°=50°;
(2)∵CD是△ABC中∠ACB的外角平分线,
∴∠ACD=∠ECD,
∵∠BAC是△ACD的外角,
∴∠BAC>∠ACD,
∴∠BAC>∠ECD,
∵∠ECD是△BCD的外角,
∴∠ECD>∠B,
∴∠BAC>∠B.
20.解:(1)∵∠B=40°,∠ACB=80°,
∴∠BAC=180°﹣40°﹣80°=60°,
∵AE是△ABC的角平分线,
∴∠BAE=∠BAC=30°,
∵FG⊥AE,
∴∠AHG=90°,
∴∠AGF=180°﹣90°﹣30°=60°;
(2)∵AD是△ABC的高,
∴∠ADC=90°,
∵∠ACB=80°,
∴∠CAD=180°﹣90°﹣80°=10°,
∵∠BAC=60°,AE是△ABC的角平分线,
∴∠CAE=∠BAC=30°,
∴∠EAD=∠CAE﹣∠CAD=30°﹣10°=20°.
同步能力提升训练(附答案)
1.在一个直角三角形中,一个锐角等于54°,则另一个锐角的度数是( )
A.26°
B.36°
C.45°
D.56°
2.已知在Rt△ABC中,∠B=90°,∠C=35°,则∠A等于( )
A.35°
B.45°
C.55°
D.65°
3.一个三角形其中一个外角的补角等于与它不相邻的两个内角的差,则这个三角形一定是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
4.将一副三角尺按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.45°
B.65°
C.75°
D.85°
5.已知△ABC中,∠A:∠B:∠C=3:4:7,则△ABC一定是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
6.如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=48°,∠C=68°,则∠DAE的度数是( )
A.10°
B.12°
C.14°
D.16°
7.在△ABC中,∠A:∠B:∠C=1:1:4,则∠A=( )
A.30°
B.45°
C.90°
D.120°
8.如图,∠CBA=∠ACB=65°,∠ACE=15°,则∠AEC的度数是( )
A.35°
B.50°
C.65°
D.80°
9.如图,△ABC中,∠A=65°,∠B=50°,点D在BC延长线上,则∠ACD的度数是( )
A.65°
B.105°
C.115°
D.125°
10.如图,∠BCD是△ABC的一个外角,E是边AB上一点.下列结论不正确的是( )
A.∠BCD>∠A
B.∠BCD>∠1
C.∠2>∠3
D.∠BCD=∠A+∠B
11.已知AH为△ABC的高,若∠B=40°,∠ACH=65°,则∠BAC的度数为
°.
12.如图,∠ABD=15°,∠ACD=30°,∠A=45°,则∠BDC的度数为
°.
13.如图,一般轮船按箭头所示方向行驶,C处有一灯塔,当轮船从A点行驶到B点时,∠ACB=
°.
14.如图,CE是△ABC的外角∠ACD的平分线,CE交BA的延长线于点E,∠B=35°,∠E=25°,则∠ACD的度数为
.
15.将一副三角板如图放置,其中∠C=30°,∠D=45°,点E在BC边上,M,N分别为AB,DF上的点,G为三角板外一点,连接GM,GN,若∠G=50°,则∠GMB+∠BED+∠DNG=
.
16.如图,将△ABC沿着DE对折,点A落到A'处,若∠BDA′+∠CEA′=70°,则∠A=
°.
17.如图,∠B=36°,∠E=48°,∠BAE的平分线与∠BDE的平分线交于点F,则∠F=
°.
18.如图,在△ABC中,∠B=90°,D是BC上一点,AE平分∠DAC.
(1)若∠ADC=116°,∠C=26°,求∠BAE的度数.
(2)若∠ADC=m°,∠C=n°,请探求∠BAE的度数与∠ADC、∠C度数之间的关系(用含m、n的代数式表示).
19.如图,已知CD是△ABC中∠ACB的外角平分线.
(1)若∠ACE=150°,∠BAC=100°,求∠B的大小;
(2)请说明∠BAC>∠B.
20.如图,AD、AE分别是△ABC的高和角平分线,∠B=40°,∠ACB=80°.点F在BC的延长线上,FG⊥AE,垂足为H,FG与AB相交于点G.
(1)求∠AGF的度数;
(2)求∠EAD的度数.
参考答案
1.解:在一个直角三角形中,一个锐角等于54°,
∴另一个锐角的度数是:90°﹣54°=36°.
故选:B.
2.解:在Rt△ABC中,∠B=90°,∠C=35°,
则∠A=90°﹣35°=55°,
故选:C.
3.解:由题意得:这个三角形的一个内角等于与它不相邻的两个内角的差.
设这个内角为∠1,另外两个内角为∠2、∠3且∠1=∠2﹣∠3.
∵180°﹣∠1=∠2+∠3,
∴2∠2=180°.
∴∠2=90°.
∴这个三角形的是直角三角形.
故选:B.
4.解:∵∠2+60°+45°=180°,
∴∠2=75°.
∵直尺的上下两边平行,
∴∠1=∠2=75°.
故选:C.
5.解:由题意可设∠A=3x,∠B=4x,∠C=7x.
∵∠A+∠B+∠C=180°,
∴3x+4x+7x=180°.
∴x=()°.
∴7x=90°.
∴△ABC是直角三角形.
故选:B.
6.解:∵∠B=48°,∠C=68°,
∴∠BAC=180°﹣∠B﹣∠C=64°,
∵AE平分∠BAC,
∴∠EAC=BAC=32°,
∵AD是△ABC的BC边上的高,
∴∠ADC=90°,
∵∠C=68°,
∴∠DAC=90°﹣∠C=22°,
∴∠DAE=∠EAC﹣∠DAC=32°﹣22°=10°,
故选:A.
7.解:∵∠A:∠B:∠C=1:1:4且∠A+∠B+∠C=180°,
∴∠A==30°.
故选:A.
8.解:∵∠CBA=∠ACB=65°,
∴∠BAC=180°﹣∠CBA﹣∠ACB=180°﹣65°﹣65°=50°,
∴∠EAC=130°,
∵∠ACE=15°,
∴∠AEC=35°,
故选:A.
9.解:∵∠ACD是△ABC的外角,
∴∠ACD=∠A+∠B=65°+50°=115°.
故选:C.
10.解:A、∠BCD是△ABC的一个外角,则∠BCD>∠A,不符合题意.
B、∠BCD是△ABC的一个外角,则∠1是△BEC的一个外角,∠BCD与∠1无法比较大小,符合题意.
C、∠2是△AEC的一个外角,则∠2>∠3,不符合题意.
D、∠BCD是△ABC的一个外角,则∠BCD=∠A+∠B,不符合题意.
故选:B.
11.解:如图,当△ABC是钝角三角形时,
∵∠B=40°,∠ACH=65°,∠ACH=∠BAC+∠B,
∴∠BAC=∠ACH﹣∠B=65°﹣40°=25°;
如图,当△ABC是锐角三角形时,
∵∠B=40°,∠ACH=65°,∠BAC+∠ACH+∠B=180°,
∴∠BAC=180°﹣∠ACH﹣∠B=180°﹣65°﹣40°=75°.
故答案为:25或75.
12.解:延长BD交AC于点E,
∵∠CEB=∠A+∠ABD,∠BDC=∠CEB+∠ACD,
∴∠BDC=∠A+∠ABD+∠ACD,
∵∠ABD=15°,∠ACD=30°,∠A=45°,
∴∠BDC=45°+30°+15°=90°,
故答案为90.
13.解:∵∠CBD=∠A+∠C,
∴∠C=∠CBD﹣∠A
=70°﹣30°
=40°,
故答案为:40.
14.解:∵∠ECD是△BCE的外角,∠B=35°,∠E=25°,
∴∠ECD=∠B+∠E=35°+25°=60°,
∵CE是∠ACD的平分线,
∴∠ACD=2∠ECD=120°,
故答案为:120°.
15.解:∵∠C=30°,∠D=45°,
∴∠B=180°﹣∠A﹣∠C=180°﹣90°﹣30°=60°,
延长FD交MG于P点,延长AB交FP于Q点,
∴∠QBE=180°﹣∠ABC=180°﹣60°=120°,
∴∠QDE==180°﹣∠FDE=180°﹣45°=135°,
∵∠FPM=∠DNG+∠G=∠DNG+50°,
∴∠BQD=∠GMB+∠FPM=GMB+∠DNG+50°,
∠BQD+∠QDE+BED+∠QBE=360°,
∴∠GMB+∠DNG+50°+135°+∠BED+120°=360°
∴∠GMB+∠BED+∠DNG=55°,
故答案为:55°.
16.解:∵将△ABC沿着DE对折,点A落到A'处,
∴∠EDA′=∠EDA,∠DEA′=∠DEA,
∵∠BDA′+2∠EDA=180°,∠CEA′+2∠DEA=180°,
∴∠BDA′+2∠EDA+∠CEA′+2∠DEA=360°,
∵∠BDA′+∠CEA′=70°,
∴∠EDA+∠DEA=145°,
∴∠A=35°,
故答案为:35.
17.解:如图,
∵∠BAE的平分线与∠BDE的平分线交于点F,
∴∠BAM=∠FAC=∠BAC,∠EDF=∠CDF=∠EDC,
∵∠BMF=∠F+∠CDF,∠BMF=∠B+∠BAF,
∴∠F+∠CDF=∠B+∠BAF,
∴∠F=∠B+∠BAF﹣∠CDF
=∠B+∠BAC﹣∠EDC
=∠B+(∠BAC﹣∠EDC)
∵∠ECB=∠E+∠EDC=∠B+∠BAC,
∴∠BAC﹣∠EDC=∠E﹣∠B,
∴∠F=∠B+(∠E﹣∠B)
=∠E+∠B
=(∠E+∠B)
=(48°+36°)
=42°,
故答案为:42.
18.解:(1)∵∠B=90°,∠C=26°,
∴∠BAC=64°,
∵∠ADC=116°,
∴∠BAD=26°,
∴∠DAC=64°﹣26°=38°,
∵AE是∠DAC的角平分线,
∴∠DAE=19°,
∴∠BAE=∠BAD+∠DAE=26°+19°=45°;
(2)∵∠B=90°,∠C=n°,
∴∠BAC=90°﹣n°,
∵∠ADC=m°,
∴∠BAD=m°﹣90°,
∴∠DAC=∠BAC﹣∠BAD=(90°﹣n°)﹣(m°﹣90°),
∵AE是∠DAC的角平分线,
∴∠DAE=DAC=(180°﹣n°﹣m°),
∴∠BAE=∠BAD+∠DAE=m°﹣90°+(180°﹣n°﹣m°)=m°﹣n°.
19.解:(1)∵∠ACE=150°,∠BAC=100°,
∴∠B=∠ACE﹣∠BAC=150°﹣100°=50°;
(2)∵CD是△ABC中∠ACB的外角平分线,
∴∠ACD=∠ECD,
∵∠BAC是△ACD的外角,
∴∠BAC>∠ACD,
∴∠BAC>∠ECD,
∵∠ECD是△BCD的外角,
∴∠ECD>∠B,
∴∠BAC>∠B.
20.解:(1)∵∠B=40°,∠ACB=80°,
∴∠BAC=180°﹣40°﹣80°=60°,
∵AE是△ABC的角平分线,
∴∠BAE=∠BAC=30°,
∵FG⊥AE,
∴∠AHG=90°,
∴∠AGF=180°﹣90°﹣30°=60°;
(2)∵AD是△ABC的高,
∴∠ADC=90°,
∵∠ACB=80°,
∴∠CAD=180°﹣90°﹣80°=10°,
∵∠BAC=60°,AE是△ABC的角平分线,
∴∠CAE=∠BAC=30°,
∴∠EAD=∠CAE﹣∠CAD=30°﹣10°=20°.
