数学人教A版(2019)必修第二册 8.3简单几何体的表面积与体积(课件)(共108张PPT)
文档属性
| 名称 | 数学人教A版(2019)必修第二册 8.3简单几何体的表面积与体积(课件)(共108张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 00:00:00 | ||
图片预览











文档简介
(共108张PPT)
简单几何体的表面积与体积
8.3.1
棱柱、棱锥、棱台的表面积和体积
1.棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台的表面积就是围成它们的各个面的
。
面积的和
【思考】
棱柱、棱锥、棱台的表面积与其展开图的面积是否也都相等?
提示:是。棱柱、棱锥、棱台的表面积就是几何体表面的面积,它表示几何体表面的大小。常把多面体展开成平面图形,利用平面图形求多面体的表面积。
2.棱柱、棱锥、棱台的体积
棱柱:棱柱的底面面积为S,高为h,则
。
棱锥:棱锥的底面面积为S,高为h,则_______。
棱台:棱台的上、下底面面积分别为S′、S,
高为h,则______________________。
V=Sh
【思考】
棱柱、棱锥、棱台的体积之间有什么关系?
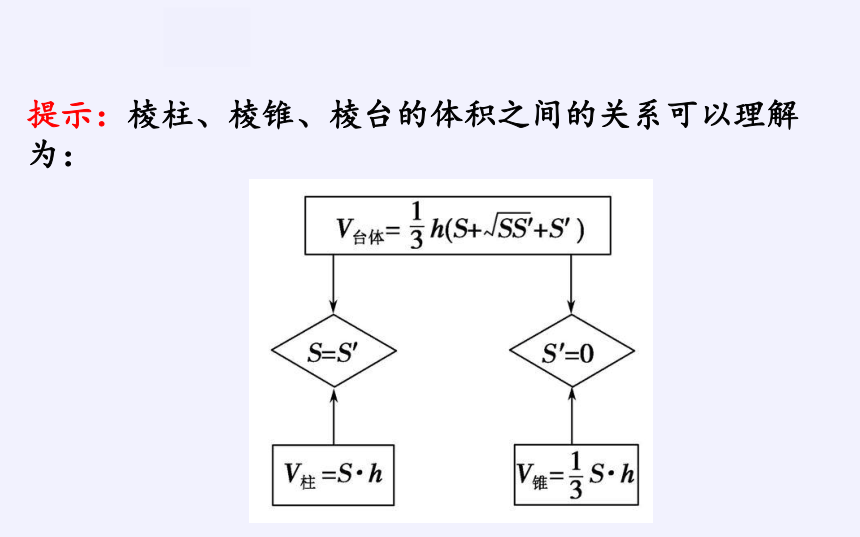
提示:棱柱、棱锥、棱台的体积之间的关系可以理解为:
【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)锥体的体积等于底面面积与高之积。( )
(2)棱台的侧面展开图是由若干个等腰梯形组成
的。( )
(3)沿不同的棱将多面体展开,得到的展开图相同,表面积相等。( )
【解析】(1)×。锥体的体积等于底面积与高之积的
。
(2)×。棱台的侧面展开图是由若干个梯形组成的,不一定是等腰梯形。
(3)×。由于剪开的棱不同,同一个几何体的表面展开图可能不相同。但是,不论怎么剪,同一个多面体表面展开图的面积是一样的。
2.正方体的表面积为96,则正方体的体积为( )
A.48
B.64
C.16
D.96
【解析】选B。设正方体的棱长为a,则6a2=96,所以a=4。所以其体积V=a3=43=64。
3.已知某长方体同一顶点上的三条棱长分别为1,2,3,则该长方体的表面积为
( )
A.22
B.20
C.10
D.11
【解析】选A。所求长方体的表面积S=2×(1×2)+2×(1×3)+2×(2×3)=22。
4.若长方体的长、宽、高分别为3cm、4cm、5cm,则长方体的体积为( )
A.27cm3
B.60cm3
C.64cm3
D.125cm3
【解析】选B。长方体即为四棱柱,其体积为底面积×高,即为3×4×5=60(cm3)。
类型一 棱柱、棱锥、棱台的表面积
【典例】1.侧面都是等腰直角三角形的正三棱锥,底面边长为a时,该三棱锥的表面积是( )
2.现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5,求该直四棱柱的表面积。
【思维·引】分别求出各个面的面积,表面积等于各个面的面积之和。
【解析】1.选A。设正三棱锥的侧棱长为b,
则由条件知,b2+b2=a2,即b2=
a2,所以
S表=
2.如图,设底面对角线AC=a,BD=b,交点为O,
对角线A1C=15,B1D=9,
所以a2+52=152,b2+52=92所以a2=200,b2=56。
所以a=10
,b=2
,
因为该直四棱柱的底面是菱形,
所以AB2=
=64,所以AB=8。
所以直四棱柱的侧面积S侧=4×8×5=160。
又因为四边形ABCD为菱形,所以S菱形=
AC·BD=
×10
×2
=20
,所以S表=2S菱形+S侧
=2×20
+160=40
+160。
【内化·悟】
怎样求多面体的表面积?
提示:多面体的表面积就是各个面的面积之和,也可以先求出侧面展开图面积,再分别求上、下底面的面积,再求总的表面积。
【类题·通】
棱锥或棱台的表面积计算常借助侧面三角形或梯形的高、侧棱及其在底面的射影与高、底面边长等构成的直角三角形(或梯形)求解。
【习练·破】
已知四棱台的上、下底面分别是边长为4和8的正方形,侧面是腰长为8的等腰梯形,则该四棱台的表面积为________。?
【解析】如图,在四棱台ABCD-A1B1C1D1中,过B1作
B1F⊥BC,垂足为F,在Rt△B1FB中,BF=
×(8-4)
=2,B1B=8,
故B1F=
所以
×(8+4)×2
=12
,
故四棱台的侧面积S侧=4×12
=48
,
所以S表=48
+4×4+8×8=80+48
。
答案:80+48
类型二 棱柱、棱锥、棱台的体积
【典例】如图所示,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比。
【思维·引】先求出棱锥的体积,再求得剩余部分的体积,最后求得体积之比。
【解析】方法一:设AB=a,AD=b,DD′=c,
则长方体ABCD-A′B′C′D′的体积V=abc,
又S△A′DD′=
bc且三棱锥C-A′DD′的高为CD=a。
所以V三棱锥C-A′DD′=
S△A′D′D·CD=
abc。
则剩余部分的几何体体积V剩=abc-
abc=
abc。
故V棱锥C-A′DD′∶V剩=
abc∶
abc=1∶5。
方法二:已知长方体可以看成侧棱垂直于底面的四棱
柱ADD′A′-BCC′B′,设它的底面ADD′A′面积为
S,高为h,则它的体积为V=Sh。而棱锥C-A′DD′的
底面面积为
S,高为h,
因此棱锥C-A′DD′的体积VC-A′DD′=
×
Sh=
Sh。
剩余部分的体积是Sh-
Sh=
Sh。
所以棱锥C-A′DD′的体积与剩余部分的体积之比为
Sh∶
Sh=1∶5。
【内化·悟】
怎样求几何体的体积?
提示:求几何体的体积,关键是弄清该几何体是柱体,锥体还是台体,再分别选择公式求解。
【类题·通】
常见的求几何体体积的方法
(1)公式法:直接代入公式求解。
(2)等积法:如四面体的任何一个面都可以作为底面,只需选用底面积和高都易求的形式即可。
(3)分割法:将几何体分割成易求解的几部分,分别求体积。
【习练·破】
如图所示,正方体ABCD-A1B1C1D1的棱长为a,过顶点B,D,A1截下一个三棱锥,则剩余部分的体积为________。?
【解析】
S△ABD·A1A=
×
a2·a
=
a3。故剩余部分的体积V=V正方体-
=a3-
=
a3。
答案:
a3
类型三 棱柱、棱锥、棱台的表面积、体积的综合应用
角度1 等积变换法求体积
【典例】如图所示,正方体ABCD-A1B1C1D1的棱长为1,
E为线段B1C上的一点,则三棱锥A-DED1的体积为
________。?
【思维·引】把三棱锥A-DED1转换为三棱锥E-DD1A,底面为直角三角形DAD1,高为正方体的棱长。
【解析】
答案:
【素养·探】
等积转换法是求锥体体积的常用方法,特别是当题目中某些点是不固定的点时,常用等积转换固定一个面,再进行求值。在解题过程中主要考查直观想象和数学运算的核心素养。把本例改为:如图所示,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,求三棱锥D1-EDF的体积。
【解析】
角度2 等体积法求点到面的距离
【典例】如图,在棱长为a的正方体ABCD-A1B1C1D1中,求点A到平面A1BD的距离d。
【思维·引】先求出三棱锥A-BDA1的体积,再求出三角形BDA1的面积,再根据等体积法求点到平面的距离。
【解析】在三棱锥A1-ABD中,AA1⊥平面ABD,AB=AD=AA1=a,A1B=BD=A1D=
a,
因为
所以
所以d=
a。所以点A到平面A1BD的距离为
a。
【类题·通】
利用等体积法求点到面的距离,一般是先选择适当的顶点求出锥体的体积,再改变顶点,求题目给出平面的面积,再用等体积法求点到面的距离。
【习练·破】
已知正四棱锥的底面边长为6,侧棱长为5,则此棱锥的侧面积为
( )
A.6
B.12
C.24
D.48
【解析】选D。正四棱锥的斜高h′=
=4,
S侧=4×
×6×4=48。
8.3.2
圆柱、圆锥、圆台、球的表面积和体积
1.圆柱、圆锥、圆台的表面积公式
【思考】
圆柱、圆锥、圆台的侧面积公式之间有什么关系?
提示:圆柱、圆锥、圆台的侧面积公式之间的关系:
S圆柱侧=2πrl
S圆台侧=π(r′+r)l
S圆锥侧=πrl。
2.圆柱、圆锥、圆台的体积公式
柱体的体积公式V=Sh(S为底面面积,h为高);
锥体的体积公式V=
Sh(S为底面面积,h为高);
台体的体积公式V=
(S′+
+S)h。
【思考】
圆柱、圆锥、圆台的体积公式之间有什么关系?
提示:柱体、锥体、台体的体积公式之间的关系:
V=Sh
V=
(S′+
+S)h
V=
Sh。
3.球的表面积和体积公式
设球的半径为R,则球的表面积S=4πR2,即球的表面
积等于它的大圆面积的4倍。球的体积V=
πR3。
【思考】
如何理解、把握球的表面积、体积公式?
提示:把握住球的表面积公式S球=4πR2,球的体积公式V球=
πR3是计算球的表面积和体积的关键,半径与球心是确定球的条件。把握住公式,球的体积与表面积计算的相关题目也就迎刃而解了。
【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)球的体积之比等于半径比的平方。
( )
(2)长方体既有外接球又有内切球。
( )
(3)球面展开一定是平面的圆面。
( )
(4)圆台的高就是相应母线的长。
( )
【解析】(1)×。球的体积之比等于半径比的立方。
(2)×。长方体只有外接球,没有内切球。
(3)×。球的表面不能展开成平面图形。
(4)×。圆台的高是指两个底面之间的距离。
2.两个球的半径之比为1∶3,那么两个球的表面积之比为( )
A.1∶9
B.1∶27
C.1∶3
D.1∶1
【解析】选A。由表面积公式知,两球的表面积之比
为
=1∶9。
3.已知一个圆柱的侧面展开图是一个正方形,这个圆柱的表面积与侧面积的比是( )
【解析】选A。设圆柱底面半径、母线长分别为r,l,
由题意知l=2πr,S侧=l2=4π2r2。
S表=S侧+2πr2=4π2r2+2πr2=2πr2(2π+1),
4.圆锥的母线长为5,底面半径为3,则其体积为( )
A.15π
B.30π
C.12π
D.36π
【解析】选C。设圆锥的高为h,如图,则h=
所以其体积V=
Sh=
×π×32×4=12π。
类型一 圆柱、圆锥、圆台、球的表面积
【典例】1.已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )
A.12
π
B.12π
C.8
π
D.10π
2.若球的过球心的截面圆的周长是C,则这个球的表面积是( )
A.
B.
C.
D.2πC2
3.已知某圆锥的底面半径为8,高为6,则该圆锥的表面积为________。?
【思维·引】1.根据条件画出图形,根据圆柱的侧面展开图求出圆柱的底面半径。
2.根据已知大圆周长求出大圆半径即球的半径,再求球的表面积。
3.根据圆锥的底面半径和高求出圆锥的母线长。
【解析】1.选B。因为过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,所以圆柱的高为2
,底面圆的直径为2
,所以该圆柱的表面积为2×π×(
)2+2π×
×2
=12π。
2.选C。由题意知大圆的半径即球的半径,设为R,
由2πR=C,得R=
,所以S球面=4πR2=
。
3.由题意,得该圆锥的母线长l=
=10,
所以该圆锥的侧面积为π×8×10=80π,底面积为π×82=64π,所以该圆锥的表面积为80π+64π=144π。
答案:144π
【内化·悟】
怎样求圆柱、圆锥、圆台的表面积?
提示:求圆柱、圆锥、圆台的表面积,关键是求出底面圆的半径,圆柱、圆锥、圆台的高及母线长。
【类题·通】
1.圆柱、圆锥、圆台的表面积的求解步骤:解决圆柱、圆锥、圆台的表面积问题,要利用好旋转体的轴截面及侧面展开图,借助平面几何知识,求得所需几何要素,代入公式求解即可,基本步骤如下:
(1)得到空间几何体的平面展开图。
(2)依次求出各个平面图形的面积。
(3)将各平面图形的面积相加。
2.球的表面积的求法
要求球的表面积,关键是知道半径R或者通过条件能求出半径R,然后代入球的表面积公式求解。
【习练·破】
1.过球一条半径的中点,作一垂直于这个半径的截面,截面面积为48π
cm2,则球的表面积为____cm2。?
【解析】易知截面为一圆面,如图所示,圆O是球的过已知半径的大圆,AB是截面圆的直径,作OC垂直AB于点C,连接OA。由截面面积为48π
cm2,可得AC=4
cm。设OA=R
cm,则OC=
R
cm,所以
R2-
=(4
)2,解得R=8。故球的表面积S=4πR2=256π(cm2)。
答案:256π
2.如图所示,已知直角梯形ABCD,BC∥AD,∠ABC=90°,AB=5cm,BC=16cm,AD=4cm。求以BC所在直线为轴旋转一周所得几何体的表面积。
【解析】以BC所在直线为轴旋转一周所得几何体是圆柱和圆锥的组合体,如图所示:
其中圆锥的高为16-4=12(cm),圆柱的母线长为
AD=4cm,故该几何体的表面积为2π×5×4+π×
52+π×5×13=130π(cm2)。
类型二 圆柱、圆锥、圆台、球的体积
【典例】1.圆锥的轴截面是等腰直角三角形,
侧面积是16
π,则圆锥的体积是( )
A.
B.
C.64π
D.128
π
2.棱台的上、下底面面积分别是2,4,高为3,则该棱台的体积是( )
A.18+6
B.6+2
C.24
D.18
3.用与球心距离为1的平面去截球,所得的截面面积
为π,则球的体积为( )
【思维·引】1.先由侧面积求出圆锥的底面半径和高,再求体积。
2.直接利用公式求体积即可。
3.根据与球心距离为1的平面去截球,所得的截面面积为π,先求出小圆的半径,再求球的半径,进而求出球的体积。
【解析】1.选A。设圆锥的底面半径为r,母线长为l,
因为圆锥的轴截面是等腰直角三角形,所以2r=
即l=
r,由题意得,侧面积S侧=πr·l=
πr2=16
π,
所以r=4。所以l=4
,高h=
=4。
所以圆锥的体积V=
Sh=
π×42×4=
π。
2.选B。V=
(S+
+S′)h=
×(2+
+4)×3
=6+2
。
3.选D。设截面圆的半径为r,则πr2=π,故r=1,
由勾股定理求得球的半径为
,所以球的
体积为
【内化·悟】
如何利用圆柱、圆锥、圆台的体积公式巧解题?
提示:利用圆柱、圆锥、圆台的体积公式解题时,首先要记准、记清公式,根据题目给出的已知条件求出底面半径和几何体的高,再利用公式求解即可。
【类题·通】
求几何体体积的常用方法
(1)公式法:直接代入公式求解。
(2)等积法:例如四面体的任何一个面都可以作为底面,只需选用底面积和高都易求的形式即可。
(3)补体法:将几何体补成易求解的几何体,如棱锥补成棱柱,棱台补成棱锥等。
(4)分割法:将几何体分割成易求解的几部分,分别求体积。
【习练·破】
1.若一个圆锥的轴截面(过圆锥顶点和底面直径的
截面)是面积为
的等边三角形,则该圆锥的体积
为( )
【解析】选B。设圆锥底面圆的半径为r,则圆锥的高为
r。由题意,得
×(2r)2=
,得r=1,所以该圆
锥的体积V=
π×12×
=
π。
2.已知Rt△ABC中,C=90°,分别以AC,BC,AB所在直线为轴旋转一周所得三个几何体的体积分别为V1,V2,V。求证:
【证明】如图,设AC=b,BC=a,作CH⊥AB于H,
则AB=
。由射影定理,得AH=
BH=
,CH2=AH·BH=
三个几何体分别是两个圆锥和组合体(有公共底面的
圆锥组合体),依题意,得V1=
πS1h1=
πa2b,
V2=
S2h2=
πb2a,V=
π·CH2·AB
所以
类型三 与球有关的切、接问题
【典例】1.将棱长为2的正方体木块削成一个体积最大的球,则该球的体积为
( )
2.长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为________。
【思维·引】1.把正方体削成一个体积最大的球,该球是正方体的内切球,球的直径就是正方体的棱长。
2.球是长方体的外接球,球的直径是长方体的体对角线。
【解析】1.选A。球的直径是正方体的棱长,
所以2R=2,R=1。所以V=
πR3=
π。
2.球的直径是长方体的体对角线,
所以2R=
S=4πR2=14π。
答案:14π
【类题·通】
球的切接问题处理策略及常用结论
(1)在处理与球有关的相接、相切问题时,一般要通过作一适当的截面,将立体问题转化为平面问题解决,而这类截面往往指的是圆锥的轴截面、球的大圆等。
(2)几个常用结论
①球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;
②球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径;
③球与圆柱的底面和侧面均相切,则球的直径等于圆柱的高,也等于圆柱底面圆的直径;
④球与棱锥相切,则可利用V棱锥=
S底h=
S表R,求球的半径R。
【习练·破】
1.棱长为2的正方体的各个顶点均在同一球面上,求此球的体积。
【解析】正方体的外接球直径等于正方体的体对角线
长,即2R=
,所以R=
,
所以V球=
·π·(
)3=4
π。
2.棱长为a的正四面体的各个顶点都在半径为R的球面上,求其外接球的表面积。
【解析】把正四面体放在正方体中,设正方体棱长
为x,则a=
x,由题意2R=
所以R=
a,所以S球=4πR2=
a2π。
3.三棱锥的三条侧棱两两垂直,且其长分别为2a,a,a,求其外接球的表面积和体积。
【解析】以三棱锥的三条侧棱为长方体从一顶点出发
的三条棱,将三棱锥补成长方体,则该长方体的外接球即为三棱锥的外接球,其球的直径等于长方体的体对角线长,故2R=
R=
a,所以S球=4πR2=6a2π,
V球=
谢
谢
简单几何体的表面积与体积
8.3.1
棱柱、棱锥、棱台的表面积和体积
1.棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台的表面积就是围成它们的各个面的
。
面积的和
【思考】
棱柱、棱锥、棱台的表面积与其展开图的面积是否也都相等?
提示:是。棱柱、棱锥、棱台的表面积就是几何体表面的面积,它表示几何体表面的大小。常把多面体展开成平面图形,利用平面图形求多面体的表面积。
2.棱柱、棱锥、棱台的体积
棱柱:棱柱的底面面积为S,高为h,则
。
棱锥:棱锥的底面面积为S,高为h,则_______。
棱台:棱台的上、下底面面积分别为S′、S,
高为h,则______________________。
V=Sh
【思考】
棱柱、棱锥、棱台的体积之间有什么关系?
提示:棱柱、棱锥、棱台的体积之间的关系可以理解为:
【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)锥体的体积等于底面面积与高之积。( )
(2)棱台的侧面展开图是由若干个等腰梯形组成
的。( )
(3)沿不同的棱将多面体展开,得到的展开图相同,表面积相等。( )
【解析】(1)×。锥体的体积等于底面积与高之积的
。
(2)×。棱台的侧面展开图是由若干个梯形组成的,不一定是等腰梯形。
(3)×。由于剪开的棱不同,同一个几何体的表面展开图可能不相同。但是,不论怎么剪,同一个多面体表面展开图的面积是一样的。
2.正方体的表面积为96,则正方体的体积为( )
A.48
B.64
C.16
D.96
【解析】选B。设正方体的棱长为a,则6a2=96,所以a=4。所以其体积V=a3=43=64。
3.已知某长方体同一顶点上的三条棱长分别为1,2,3,则该长方体的表面积为
( )
A.22
B.20
C.10
D.11
【解析】选A。所求长方体的表面积S=2×(1×2)+2×(1×3)+2×(2×3)=22。
4.若长方体的长、宽、高分别为3cm、4cm、5cm,则长方体的体积为( )
A.27cm3
B.60cm3
C.64cm3
D.125cm3
【解析】选B。长方体即为四棱柱,其体积为底面积×高,即为3×4×5=60(cm3)。
类型一 棱柱、棱锥、棱台的表面积
【典例】1.侧面都是等腰直角三角形的正三棱锥,底面边长为a时,该三棱锥的表面积是( )
2.现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5,求该直四棱柱的表面积。
【思维·引】分别求出各个面的面积,表面积等于各个面的面积之和。
【解析】1.选A。设正三棱锥的侧棱长为b,
则由条件知,b2+b2=a2,即b2=
a2,所以
S表=
2.如图,设底面对角线AC=a,BD=b,交点为O,
对角线A1C=15,B1D=9,
所以a2+52=152,b2+52=92所以a2=200,b2=56。
所以a=10
,b=2
,
因为该直四棱柱的底面是菱形,
所以AB2=
=64,所以AB=8。
所以直四棱柱的侧面积S侧=4×8×5=160。
又因为四边形ABCD为菱形,所以S菱形=
AC·BD=
×10
×2
=20
,所以S表=2S菱形+S侧
=2×20
+160=40
+160。
【内化·悟】
怎样求多面体的表面积?
提示:多面体的表面积就是各个面的面积之和,也可以先求出侧面展开图面积,再分别求上、下底面的面积,再求总的表面积。
【类题·通】
棱锥或棱台的表面积计算常借助侧面三角形或梯形的高、侧棱及其在底面的射影与高、底面边长等构成的直角三角形(或梯形)求解。
【习练·破】
已知四棱台的上、下底面分别是边长为4和8的正方形,侧面是腰长为8的等腰梯形,则该四棱台的表面积为________。?
【解析】如图,在四棱台ABCD-A1B1C1D1中,过B1作
B1F⊥BC,垂足为F,在Rt△B1FB中,BF=
×(8-4)
=2,B1B=8,
故B1F=
所以
×(8+4)×2
=12
,
故四棱台的侧面积S侧=4×12
=48
,
所以S表=48
+4×4+8×8=80+48
。
答案:80+48
类型二 棱柱、棱锥、棱台的体积
【典例】如图所示,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比。
【思维·引】先求出棱锥的体积,再求得剩余部分的体积,最后求得体积之比。
【解析】方法一:设AB=a,AD=b,DD′=c,
则长方体ABCD-A′B′C′D′的体积V=abc,
又S△A′DD′=
bc且三棱锥C-A′DD′的高为CD=a。
所以V三棱锥C-A′DD′=
S△A′D′D·CD=
abc。
则剩余部分的几何体体积V剩=abc-
abc=
abc。
故V棱锥C-A′DD′∶V剩=
abc∶
abc=1∶5。
方法二:已知长方体可以看成侧棱垂直于底面的四棱
柱ADD′A′-BCC′B′,设它的底面ADD′A′面积为
S,高为h,则它的体积为V=Sh。而棱锥C-A′DD′的
底面面积为
S,高为h,
因此棱锥C-A′DD′的体积VC-A′DD′=
×
Sh=
Sh。
剩余部分的体积是Sh-
Sh=
Sh。
所以棱锥C-A′DD′的体积与剩余部分的体积之比为
Sh∶
Sh=1∶5。
【内化·悟】
怎样求几何体的体积?
提示:求几何体的体积,关键是弄清该几何体是柱体,锥体还是台体,再分别选择公式求解。
【类题·通】
常见的求几何体体积的方法
(1)公式法:直接代入公式求解。
(2)等积法:如四面体的任何一个面都可以作为底面,只需选用底面积和高都易求的形式即可。
(3)分割法:将几何体分割成易求解的几部分,分别求体积。
【习练·破】
如图所示,正方体ABCD-A1B1C1D1的棱长为a,过顶点B,D,A1截下一个三棱锥,则剩余部分的体积为________。?
【解析】
S△ABD·A1A=
×
a2·a
=
a3。故剩余部分的体积V=V正方体-
=a3-
=
a3。
答案:
a3
类型三 棱柱、棱锥、棱台的表面积、体积的综合应用
角度1 等积变换法求体积
【典例】如图所示,正方体ABCD-A1B1C1D1的棱长为1,
E为线段B1C上的一点,则三棱锥A-DED1的体积为
________。?
【思维·引】把三棱锥A-DED1转换为三棱锥E-DD1A,底面为直角三角形DAD1,高为正方体的棱长。
【解析】
答案:
【素养·探】
等积转换法是求锥体体积的常用方法,特别是当题目中某些点是不固定的点时,常用等积转换固定一个面,再进行求值。在解题过程中主要考查直观想象和数学运算的核心素养。把本例改为:如图所示,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,求三棱锥D1-EDF的体积。
【解析】
角度2 等体积法求点到面的距离
【典例】如图,在棱长为a的正方体ABCD-A1B1C1D1中,求点A到平面A1BD的距离d。
【思维·引】先求出三棱锥A-BDA1的体积,再求出三角形BDA1的面积,再根据等体积法求点到平面的距离。
【解析】在三棱锥A1-ABD中,AA1⊥平面ABD,AB=AD=AA1=a,A1B=BD=A1D=
a,
因为
所以
所以d=
a。所以点A到平面A1BD的距离为
a。
【类题·通】
利用等体积法求点到面的距离,一般是先选择适当的顶点求出锥体的体积,再改变顶点,求题目给出平面的面积,再用等体积法求点到面的距离。
【习练·破】
已知正四棱锥的底面边长为6,侧棱长为5,则此棱锥的侧面积为
( )
A.6
B.12
C.24
D.48
【解析】选D。正四棱锥的斜高h′=
=4,
S侧=4×
×6×4=48。
8.3.2
圆柱、圆锥、圆台、球的表面积和体积
1.圆柱、圆锥、圆台的表面积公式
【思考】
圆柱、圆锥、圆台的侧面积公式之间有什么关系?
提示:圆柱、圆锥、圆台的侧面积公式之间的关系:
S圆柱侧=2πrl
S圆台侧=π(r′+r)l
S圆锥侧=πrl。
2.圆柱、圆锥、圆台的体积公式
柱体的体积公式V=Sh(S为底面面积,h为高);
锥体的体积公式V=
Sh(S为底面面积,h为高);
台体的体积公式V=
(S′+
+S)h。
【思考】
圆柱、圆锥、圆台的体积公式之间有什么关系?
提示:柱体、锥体、台体的体积公式之间的关系:
V=Sh
V=
(S′+
+S)h
V=
Sh。
3.球的表面积和体积公式
设球的半径为R,则球的表面积S=4πR2,即球的表面
积等于它的大圆面积的4倍。球的体积V=
πR3。
【思考】
如何理解、把握球的表面积、体积公式?
提示:把握住球的表面积公式S球=4πR2,球的体积公式V球=
πR3是计算球的表面积和体积的关键,半径与球心是确定球的条件。把握住公式,球的体积与表面积计算的相关题目也就迎刃而解了。
【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)球的体积之比等于半径比的平方。
( )
(2)长方体既有外接球又有内切球。
( )
(3)球面展开一定是平面的圆面。
( )
(4)圆台的高就是相应母线的长。
( )
【解析】(1)×。球的体积之比等于半径比的立方。
(2)×。长方体只有外接球,没有内切球。
(3)×。球的表面不能展开成平面图形。
(4)×。圆台的高是指两个底面之间的距离。
2.两个球的半径之比为1∶3,那么两个球的表面积之比为( )
A.1∶9
B.1∶27
C.1∶3
D.1∶1
【解析】选A。由表面积公式知,两球的表面积之比
为
=1∶9。
3.已知一个圆柱的侧面展开图是一个正方形,这个圆柱的表面积与侧面积的比是( )
【解析】选A。设圆柱底面半径、母线长分别为r,l,
由题意知l=2πr,S侧=l2=4π2r2。
S表=S侧+2πr2=4π2r2+2πr2=2πr2(2π+1),
4.圆锥的母线长为5,底面半径为3,则其体积为( )
A.15π
B.30π
C.12π
D.36π
【解析】选C。设圆锥的高为h,如图,则h=
所以其体积V=
Sh=
×π×32×4=12π。
类型一 圆柱、圆锥、圆台、球的表面积
【典例】1.已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )
A.12
π
B.12π
C.8
π
D.10π
2.若球的过球心的截面圆的周长是C,则这个球的表面积是( )
A.
B.
C.
D.2πC2
3.已知某圆锥的底面半径为8,高为6,则该圆锥的表面积为________。?
【思维·引】1.根据条件画出图形,根据圆柱的侧面展开图求出圆柱的底面半径。
2.根据已知大圆周长求出大圆半径即球的半径,再求球的表面积。
3.根据圆锥的底面半径和高求出圆锥的母线长。
【解析】1.选B。因为过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,所以圆柱的高为2
,底面圆的直径为2
,所以该圆柱的表面积为2×π×(
)2+2π×
×2
=12π。
2.选C。由题意知大圆的半径即球的半径,设为R,
由2πR=C,得R=
,所以S球面=4πR2=
。
3.由题意,得该圆锥的母线长l=
=10,
所以该圆锥的侧面积为π×8×10=80π,底面积为π×82=64π,所以该圆锥的表面积为80π+64π=144π。
答案:144π
【内化·悟】
怎样求圆柱、圆锥、圆台的表面积?
提示:求圆柱、圆锥、圆台的表面积,关键是求出底面圆的半径,圆柱、圆锥、圆台的高及母线长。
【类题·通】
1.圆柱、圆锥、圆台的表面积的求解步骤:解决圆柱、圆锥、圆台的表面积问题,要利用好旋转体的轴截面及侧面展开图,借助平面几何知识,求得所需几何要素,代入公式求解即可,基本步骤如下:
(1)得到空间几何体的平面展开图。
(2)依次求出各个平面图形的面积。
(3)将各平面图形的面积相加。
2.球的表面积的求法
要求球的表面积,关键是知道半径R或者通过条件能求出半径R,然后代入球的表面积公式求解。
【习练·破】
1.过球一条半径的中点,作一垂直于这个半径的截面,截面面积为48π
cm2,则球的表面积为____cm2。?
【解析】易知截面为一圆面,如图所示,圆O是球的过已知半径的大圆,AB是截面圆的直径,作OC垂直AB于点C,连接OA。由截面面积为48π
cm2,可得AC=4
cm。设OA=R
cm,则OC=
R
cm,所以
R2-
=(4
)2,解得R=8。故球的表面积S=4πR2=256π(cm2)。
答案:256π
2.如图所示,已知直角梯形ABCD,BC∥AD,∠ABC=90°,AB=5cm,BC=16cm,AD=4cm。求以BC所在直线为轴旋转一周所得几何体的表面积。
【解析】以BC所在直线为轴旋转一周所得几何体是圆柱和圆锥的组合体,如图所示:
其中圆锥的高为16-4=12(cm),圆柱的母线长为
AD=4cm,故该几何体的表面积为2π×5×4+π×
52+π×5×13=130π(cm2)。
类型二 圆柱、圆锥、圆台、球的体积
【典例】1.圆锥的轴截面是等腰直角三角形,
侧面积是16
π,则圆锥的体积是( )
A.
B.
C.64π
D.128
π
2.棱台的上、下底面面积分别是2,4,高为3,则该棱台的体积是( )
A.18+6
B.6+2
C.24
D.18
3.用与球心距离为1的平面去截球,所得的截面面积
为π,则球的体积为( )
【思维·引】1.先由侧面积求出圆锥的底面半径和高,再求体积。
2.直接利用公式求体积即可。
3.根据与球心距离为1的平面去截球,所得的截面面积为π,先求出小圆的半径,再求球的半径,进而求出球的体积。
【解析】1.选A。设圆锥的底面半径为r,母线长为l,
因为圆锥的轴截面是等腰直角三角形,所以2r=
即l=
r,由题意得,侧面积S侧=πr·l=
πr2=16
π,
所以r=4。所以l=4
,高h=
=4。
所以圆锥的体积V=
Sh=
π×42×4=
π。
2.选B。V=
(S+
+S′)h=
×(2+
+4)×3
=6+2
。
3.选D。设截面圆的半径为r,则πr2=π,故r=1,
由勾股定理求得球的半径为
,所以球的
体积为
【内化·悟】
如何利用圆柱、圆锥、圆台的体积公式巧解题?
提示:利用圆柱、圆锥、圆台的体积公式解题时,首先要记准、记清公式,根据题目给出的已知条件求出底面半径和几何体的高,再利用公式求解即可。
【类题·通】
求几何体体积的常用方法
(1)公式法:直接代入公式求解。
(2)等积法:例如四面体的任何一个面都可以作为底面,只需选用底面积和高都易求的形式即可。
(3)补体法:将几何体补成易求解的几何体,如棱锥补成棱柱,棱台补成棱锥等。
(4)分割法:将几何体分割成易求解的几部分,分别求体积。
【习练·破】
1.若一个圆锥的轴截面(过圆锥顶点和底面直径的
截面)是面积为
的等边三角形,则该圆锥的体积
为( )
【解析】选B。设圆锥底面圆的半径为r,则圆锥的高为
r。由题意,得
×(2r)2=
,得r=1,所以该圆
锥的体积V=
π×12×
=
π。
2.已知Rt△ABC中,C=90°,分别以AC,BC,AB所在直线为轴旋转一周所得三个几何体的体积分别为V1,V2,V。求证:
【证明】如图,设AC=b,BC=a,作CH⊥AB于H,
则AB=
。由射影定理,得AH=
BH=
,CH2=AH·BH=
三个几何体分别是两个圆锥和组合体(有公共底面的
圆锥组合体),依题意,得V1=
πS1h1=
πa2b,
V2=
S2h2=
πb2a,V=
π·CH2·AB
所以
类型三 与球有关的切、接问题
【典例】1.将棱长为2的正方体木块削成一个体积最大的球,则该球的体积为
( )
2.长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为________。
【思维·引】1.把正方体削成一个体积最大的球,该球是正方体的内切球,球的直径就是正方体的棱长。
2.球是长方体的外接球,球的直径是长方体的体对角线。
【解析】1.选A。球的直径是正方体的棱长,
所以2R=2,R=1。所以V=
πR3=
π。
2.球的直径是长方体的体对角线,
所以2R=
S=4πR2=14π。
答案:14π
【类题·通】
球的切接问题处理策略及常用结论
(1)在处理与球有关的相接、相切问题时,一般要通过作一适当的截面,将立体问题转化为平面问题解决,而这类截面往往指的是圆锥的轴截面、球的大圆等。
(2)几个常用结论
①球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;
②球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径;
③球与圆柱的底面和侧面均相切,则球的直径等于圆柱的高,也等于圆柱底面圆的直径;
④球与棱锥相切,则可利用V棱锥=
S底h=
S表R,求球的半径R。
【习练·破】
1.棱长为2的正方体的各个顶点均在同一球面上,求此球的体积。
【解析】正方体的外接球直径等于正方体的体对角线
长,即2R=
,所以R=
,
所以V球=
·π·(
)3=4
π。
2.棱长为a的正四面体的各个顶点都在半径为R的球面上,求其外接球的表面积。
【解析】把正四面体放在正方体中,设正方体棱长
为x,则a=
x,由题意2R=
所以R=
a,所以S球=4πR2=
a2π。
3.三棱锥的三条侧棱两两垂直,且其长分别为2a,a,a,求其外接球的表面积和体积。
【解析】以三棱锥的三条侧棱为长方体从一顶点出发
的三条棱,将三棱锥补成长方体,则该长方体的外接球即为三棱锥的外接球,其球的直径等于长方体的体对角线长,故2R=
R=
a,所以S球=4πR2=6a2π,
V球=
谢
谢
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
