沪教版(上海)高一数学上册 1.5 充分条件与必要条件_2 课件(共23张PPT)
文档属性
| 名称 | 沪教版(上海)高一数学上册 1.5 充分条件与必要条件_2 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 762.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
1、命题:
可以判断真假的陈述句,可写成:若p则q。
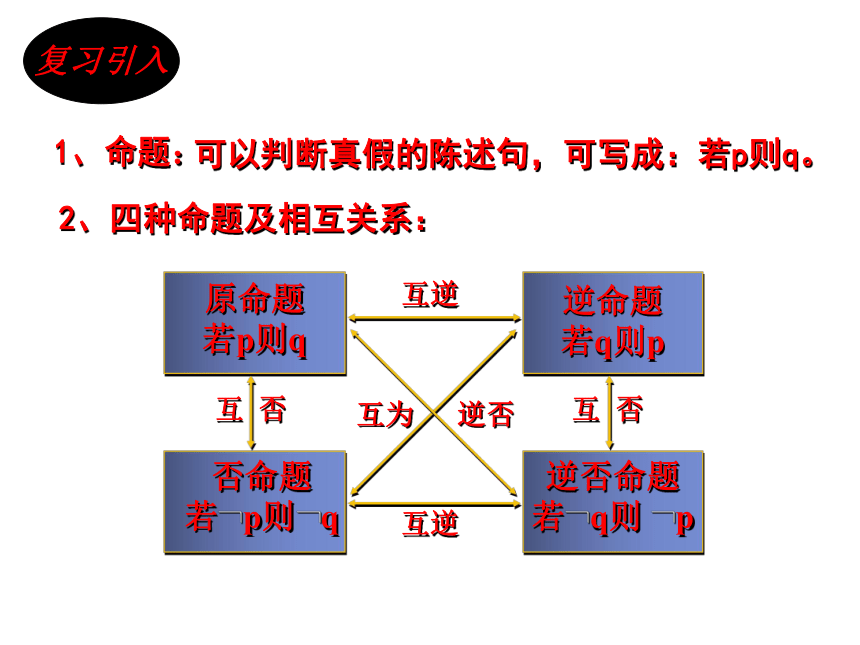
2、四种命题及相互关系:
逆命题
若q则p
原命题
若p则q
否命题
若
p则
q
逆否命题
若
q则
p
互逆
互逆
互
否
互
否
互为
逆否
复习引入
例
判断下列命题是真命题还是假命题?
(1)若x>a2+b2,则x>2ab。
(2)若ab=0,则a=0。
(3)有两角相等的三角形是等腰三角形。
(4)若a2>b2,则a>b。
复习引入
(1)、(3)为真命题。
(2)、(4)为假命题。
新课
定义:如果
,则说p是q的充分条件(sufficient
condition),
q是p的必要条件(necessary
condition).
如果命题“若p则q”为真,则记作p
q(或q
p)。
例1、
下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件?
若
x=1,则x2-4x+3=0;
若f(x)=x,则f(x)在(-∞,+∞)上为增函数;
若x为无理数,则x2为无理数
.
新课
解:命题(1)(2)是真命题,命题(3)是假命题.
所以,命题(1)(2)中的p是q的充分条件.
例2、下列“若p,则q”形式的命题中,哪些命题中的q是p的必要条件?
若x=y,则x2=y2;
若两个三角形全等,则这两个三角形的面积相等;
若a>b,则ac>bc.
新课
解:命题(1)(2)是真命题,命题(3)是假命题.
所以,命题(1)(2)中的q是p的必要条件.
新课
则说p不是q的充分条件,
q不是p的必要条件。
如果命题“若p则q”为真,则记作p
q(或q
p)
如果命题“若p则q”为假,则记作p
q
如ac=bc
a=c,
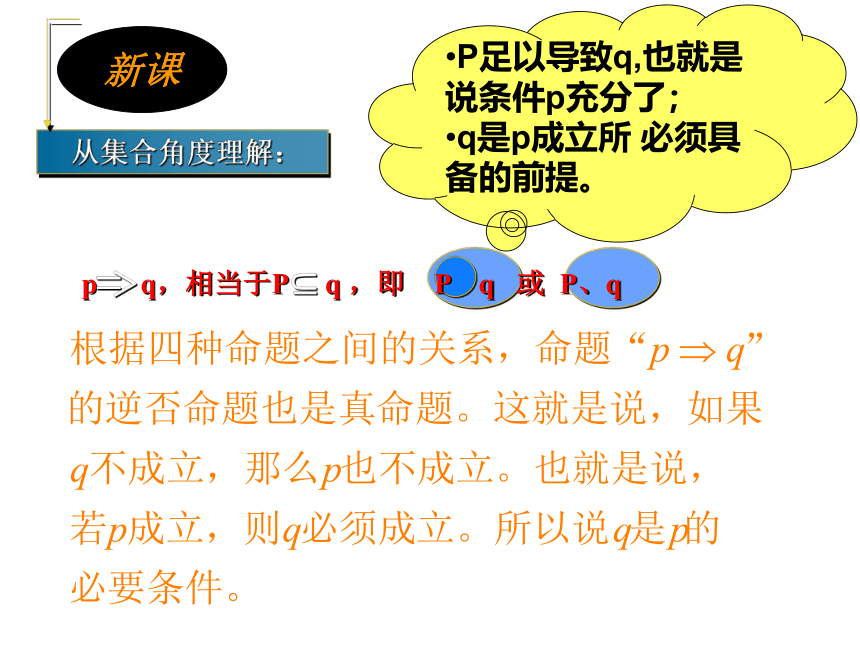
从集合角度理解:
新课
P足以导致q,也就是说条件p充分了;
q是p成立所
必须具备的前提。
p
q,相当于P
q
,即
P
q
或
P、q
例3、
判断下列命题中前者是后者的什么条件?
(1)若a>b,c>d,则a+c>b+d。
(2)ax2+ax+1>0的解集为R,则0(3)若a2>b2,则a>b。
(1)
p
q
,
q
p
(2)
p
q
,
q
p
(3)
p
q
,
q
p
前者是后者的充分不必要条件。
前者是后者的必要不充分条件。
前者是后者的既不充分也不必要条件。
新课
例4
、
判断下列问题中,p是q成立的什么条件?
p
q
(1)
x2>1
x<-1
(2)
|x-2|<4
-x2+4x+5>0
(3)
xy≠0
x≠0或y≠0
(1)、(2)
p
q,q
p
(3)p
q,q
p
(原问题
q
p)
新课
如果已知p
q,则说p是q的充分条件,
q是p的必要条件。
①
认清条件和结论。
②
考察p
q和q
p的真假。
①
可先简化命题。
③
将命题转化为等价的逆否命题后再判断。
②
否定一个命题只要举出一个反例即可。
定
义:
判别步骤:
判别技巧:
小结
p
q,相当于P
q
,即
P
q
或
P、q
从集合角度理解:
回顾
P足以导致q,也就是说条件p充分了;
q是p成立所
必须具备的前提。
充分条件与必要条件
再深入探究
按“充分、必要”把条件分类,可以分为四种类型:
⑵必要不充分条件(
)
⑶既不充分也不必要条件(
)
⑷充要条件(
)
⑴充分不必要条件(
)
例2、已知:
⊙O的半径为r,圆心O到直线l的距离为d,求证
:d=r是直线l与⊙O相切的充要条件。
证明:如图,作OP
⊥l于点P,则OP=d.
(1)充分性
:若d=r,则点p在⊙O上。在直线l上任取一点Q(异于点p),连接OQ。则OQ
>OP=r.所以,除点p外直线l上的点都在⊙O的外部,即直线l与⊙O仅有一个公共点P.所以直线l与⊙O相切。
(2)必要性
:若直线l与⊙O相切,不妨设切点为P,则OP
⊥l,因此d=OP=r.
1、命题:
可以判断真假的陈述句,可写成:若p则q。
2、四种命题及相互关系:
逆命题
若q则p
原命题
若p则q
否命题
若
p则
q
逆否命题
若
q则
p
互逆
互逆
互
否
互
否
互为
逆否
复习引入
例
判断下列命题是真命题还是假命题?
(1)若x>a2+b2,则x>2ab。
(2)若ab=0,则a=0。
(3)有两角相等的三角形是等腰三角形。
(4)若a2>b2,则a>b。
复习引入
(1)、(3)为真命题。
(2)、(4)为假命题。
新课
定义:如果
,则说p是q的充分条件(sufficient
condition),
q是p的必要条件(necessary
condition).
如果命题“若p则q”为真,则记作p
q(或q
p)。
例1、
下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件?
若
x=1,则x2-4x+3=0;
若f(x)=x,则f(x)在(-∞,+∞)上为增函数;
若x为无理数,则x2为无理数
.
新课
解:命题(1)(2)是真命题,命题(3)是假命题.
所以,命题(1)(2)中的p是q的充分条件.
例2、下列“若p,则q”形式的命题中,哪些命题中的q是p的必要条件?
若x=y,则x2=y2;
若两个三角形全等,则这两个三角形的面积相等;
若a>b,则ac>bc.
新课
解:命题(1)(2)是真命题,命题(3)是假命题.
所以,命题(1)(2)中的q是p的必要条件.
新课
则说p不是q的充分条件,
q不是p的必要条件。
如果命题“若p则q”为真,则记作p
q(或q
p)
如果命题“若p则q”为假,则记作p
q
如ac=bc
a=c,
从集合角度理解:
新课
P足以导致q,也就是说条件p充分了;
q是p成立所
必须具备的前提。
p
q,相当于P
q
,即
P
q
或
P、q
例3、
判断下列命题中前者是后者的什么条件?
(1)若a>b,c>d,则a+c>b+d。
(2)ax2+ax+1>0的解集为R,则0
(1)
p
q
,
q
p
(2)
p
q
,
q
p
(3)
p
q
,
q
p
前者是后者的充分不必要条件。
前者是后者的必要不充分条件。
前者是后者的既不充分也不必要条件。
新课
例4
、
判断下列问题中,p是q成立的什么条件?
p
q
(1)
x2>1
x<-1
(2)
|x-2|<4
-x2+4x+5>0
(3)
xy≠0
x≠0或y≠0
(1)、(2)
p
q,q
p
(3)p
q,q
p
(原问题
q
p)
新课
如果已知p
q,则说p是q的充分条件,
q是p的必要条件。
①
认清条件和结论。
②
考察p
q和q
p的真假。
①
可先简化命题。
③
将命题转化为等价的逆否命题后再判断。
②
否定一个命题只要举出一个反例即可。
定
义:
判别步骤:
判别技巧:
小结
p
q,相当于P
q
,即
P
q
或
P、q
从集合角度理解:
回顾
P足以导致q,也就是说条件p充分了;
q是p成立所
必须具备的前提。
充分条件与必要条件
再深入探究
按“充分、必要”把条件分类,可以分为四种类型:
⑵必要不充分条件(
)
⑶既不充分也不必要条件(
)
⑷充要条件(
)
⑴充分不必要条件(
)
例2、已知:
⊙O的半径为r,圆心O到直线l的距离为d,求证
:d=r是直线l与⊙O相切的充要条件。
证明:如图,作OP
⊥l于点P,则OP=d.
(1)充分性
:若d=r,则点p在⊙O上。在直线l上任取一点Q(异于点p),连接OQ。则OQ
>OP=r.所以,除点p外直线l上的点都在⊙O的外部,即直线l与⊙O仅有一个公共点P.所以直线l与⊙O相切。
(2)必要性
:若直线l与⊙O相切,不妨设切点为P,则OP
⊥l,因此d=OP=r.
