沪教版(上海)高一数学上册 1.2 集合之间的关系_4 课件(共18张PPT)
文档属性
| 名称 | 沪教版(上海)高一数学上册 1.2 集合之间的关系_4 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 577.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
集合之间的关系与运算
1.了解集合的含义、元素与集合的“属于”关系,能用自然语言、图形语言、
集合语言(列举法或描述法)描述不同的具体问题,理解集合之间包含与相等
的含义,能识别给定集合的子集,在具体情境中,了解全集与空集的含义.
2.理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集,理解
在给定集合中一个子集的补集的含义,会求给定子集的补集,能使用韦恩图
(Venn)表达集合的关系及运算.
集合与常用逻辑用语
基础自查
1.集合与元素
(1)集合元素的三个特征:确定性、
、无序性.
(2)元素与集合的关系是属于或不属于关系,用符号
或
表示.
(3)集合的表示法:列举法、
、图示法、自然语言.
(4)常用数集:自然数集N;正整数集N
(或N+);整数集Z;有理数集Q;
实数集R.
(5)集合的分类:按集合中元素个数划分,集合可以分为有限集、无限
集、
.
互异性
∈
?
描述法
空集
2.集合间的基本关系
(1)子集、真子集及其性质
对任意的x∈A,都有x∈B,则
(或
).
若A?B,且在B中至少有一个元素x∈B,但x?A,则
.
?
A;A?A;A?B,B?C?A?C.
若A含有n个元素,则A的子集有2n个,A的非空子集有
个.
(2)集合相等
若A?B且B?A,则
.
A?B
B?A
?
2n-1
A=B
3.集合的运算及其性质
(1)集合的并、交、补运算
并集:A∪B={x|x∈A或x∈B};
交集:A∩B=
;
补集:?UA={x|x∈U且x?A}.
U为全集,?UA表示A相对于全集U的补集.
(2)集合的运算性质
①A∪B=A?B?A,A∩B=A?
;
②A∩A=A,A∩?=
;
③A∪A=A,A∪?=A;
④A∩?UA=?,A∪?UA=U,?U(?UA)=A.
{x|x∈A且x∈B}
A?B
?
联动思考
想一想:子集与真子集的区别与联系?
答案:集合A的真子集一定是其子集,而集合A的子集不一定是其真子集.
议一议:怎样理解并集概念中的“或”?
答案:并集概念中“或”的意义:“x∈A,或x∈B”包括三种情况:一是x∈A
但x∈/B,二是x∈/A,x∈B,三是x∈A且x∈B,即可兼有.
联动体验
1.已知集合A={1,3,5,7,9},B={0,3,6,9,12},则A∩B等于
( )
A.{3,5}
B.{3,6}
C.{3,7}
D.{3,9}
解析:A={1,3,5,7,9},B={0,3,6,9,12},A和B中有相同的元素3,9,
∴A∩B={3,9}.
答案:D
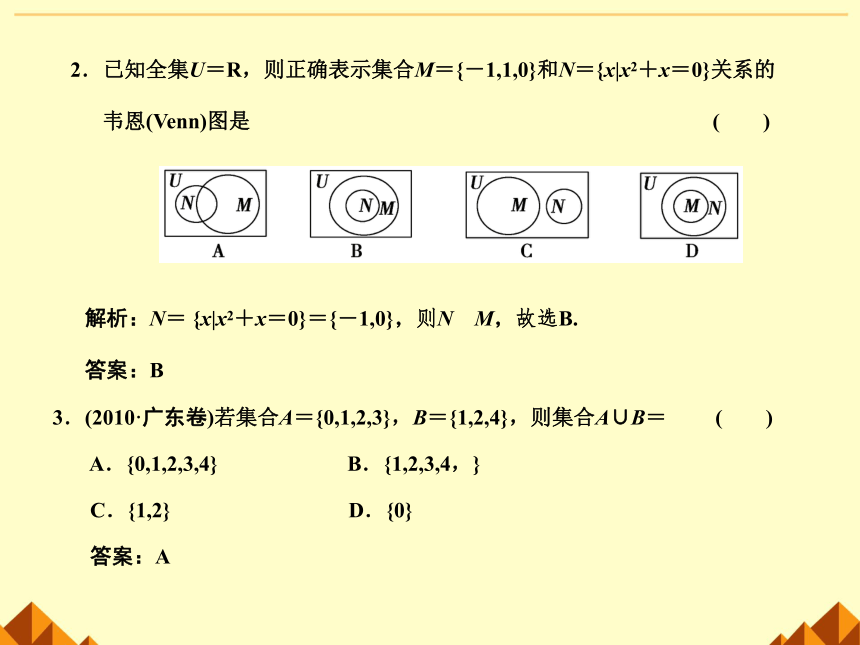
2.已知全集U=R,则正确表示集合M={-1,1,0}和N={x|x2+x=0}关系的
韦恩(Venn)图是
( )
解析:N=
{x|x2+x=0}={-1,0},则N?M,故选B.
答案:B
3.(2010·广东卷)若集合A={0,1,2,3},B={1,2,4},则集合A∪B=
( )
A.{0,1,2,3,4}
B.{1,2,3,4,}
C.{1,2}
D.{0}
答案:A
4.(2010·山东卷)已知全集U=R,集合M={x|x2-4≤0}则?UM=
( )
A.{x|-2<x<2}
B.{x|-2≤x≤2}
C.{x|x<-2或x>2}
D.{x|x≤-2或x≥2}
解析:M={x|x2-4≤0}={x|-2≤x≤2}∴?UM={x|x<-2或x>2}.
答案:C
5.已知集合A={-1,3,m},集合B={3,4},若B?A,则实数m=________.
解析:∵B?A,∴4∈B?4∈A?m=4.
答案:4
考向一 集合的基本概念
考向二 集合间的基本关系
反思感悟:善于总结,养成习惯
对于含有参数的问题,求解的基本策略是分类讨论,在分类讨论时要把字母参数的各种可能情况都考虑进去,特别注意不要遗漏了参数等于零的情况.
迁移发散
2.已知集合A={x|x2-3x-10≤0},
(1)若B?A,B={x|m+1≤x≤2m-1},求实数m的取值范围;
(2)若A?B,B={x|m-6≤x≤2m-1},求实数m的取值范围;
(3)若A=B,B={x|m-6≤x≤2m-1},求实数m的取值范围.
解:(1)由A={x|x2-3x-10≤0},得
A={x|-2≤x≤5},
∵B?A,∴①若B=?,
则m+1>2m-1,
即m<2,此时满足B?A.
考向三 集合的基本运算
反思感悟:善于总结,养成习惯
1.求一个集合在指定集合中的补集,其一般方法是把这个集合法求出来,再根
据补集的含义求解
2.在解对数不等式时一定要注意对数函数的定义域本身对变量的限制条件,不
然就会扩大解的范围,同时注意对数函数性质的应用,把对数不等式转化为
一般的代数不等式.
迁移发散
3.设集合A={x|0≤x≤4},B={y|y=-x2,-1≤x≤2},则?R(A∩B)
等于
( )
A.R
B.{x|x∈R,x≠0}
C.{0}
D.?
解析:B={y|y=-x2,-1≤x≤2}=[-4,0],则A∩B={0},∴?R(A∩B)
={x|x∈R,x≠0}.
答案:B
课堂总结
感悟提升
1.集合中的元素的三个性质,特别是无序性和互异性在解题时经常用到.解题
后要进行检验,要重视符号语言与文字语言之间的相互转化.
2.空集在解题时有特殊地位,它是任何集合的子集,是任何非空集合的真子
集,时刻关注对空集的讨论,防止漏掉.
3.解题时注意区分两大关系:一是元素与集合的从属关系;二是集合与集合的
包含关系.
4.解答集合题目,认清集合元素的属性(是点集、数集或其他情形)和化简集合
是正确求解的两个先决条件.
5.韦恩图示法和数轴图示法是进行集合交、并、补运算的常用方法,其中运用
数轴图示法要特别注意端点是实心点还是空心点.
集合之间的关系与运算
1.了解集合的含义、元素与集合的“属于”关系,能用自然语言、图形语言、
集合语言(列举法或描述法)描述不同的具体问题,理解集合之间包含与相等
的含义,能识别给定集合的子集,在具体情境中,了解全集与空集的含义.
2.理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集,理解
在给定集合中一个子集的补集的含义,会求给定子集的补集,能使用韦恩图
(Venn)表达集合的关系及运算.
集合与常用逻辑用语
基础自查
1.集合与元素
(1)集合元素的三个特征:确定性、
、无序性.
(2)元素与集合的关系是属于或不属于关系,用符号
或
表示.
(3)集合的表示法:列举法、
、图示法、自然语言.
(4)常用数集:自然数集N;正整数集N
(或N+);整数集Z;有理数集Q;
实数集R.
(5)集合的分类:按集合中元素个数划分,集合可以分为有限集、无限
集、
.
互异性
∈
?
描述法
空集
2.集合间的基本关系
(1)子集、真子集及其性质
对任意的x∈A,都有x∈B,则
(或
).
若A?B,且在B中至少有一个元素x∈B,但x?A,则
.
?
A;A?A;A?B,B?C?A?C.
若A含有n个元素,则A的子集有2n个,A的非空子集有
个.
(2)集合相等
若A?B且B?A,则
.
A?B
B?A
?
2n-1
A=B
3.集合的运算及其性质
(1)集合的并、交、补运算
并集:A∪B={x|x∈A或x∈B};
交集:A∩B=
;
补集:?UA={x|x∈U且x?A}.
U为全集,?UA表示A相对于全集U的补集.
(2)集合的运算性质
①A∪B=A?B?A,A∩B=A?
;
②A∩A=A,A∩?=
;
③A∪A=A,A∪?=A;
④A∩?UA=?,A∪?UA=U,?U(?UA)=A.
{x|x∈A且x∈B}
A?B
?
联动思考
想一想:子集与真子集的区别与联系?
答案:集合A的真子集一定是其子集,而集合A的子集不一定是其真子集.
议一议:怎样理解并集概念中的“或”?
答案:并集概念中“或”的意义:“x∈A,或x∈B”包括三种情况:一是x∈A
但x∈/B,二是x∈/A,x∈B,三是x∈A且x∈B,即可兼有.
联动体验
1.已知集合A={1,3,5,7,9},B={0,3,6,9,12},则A∩B等于
( )
A.{3,5}
B.{3,6}
C.{3,7}
D.{3,9}
解析:A={1,3,5,7,9},B={0,3,6,9,12},A和B中有相同的元素3,9,
∴A∩B={3,9}.
答案:D
2.已知全集U=R,则正确表示集合M={-1,1,0}和N={x|x2+x=0}关系的
韦恩(Venn)图是
( )
解析:N=
{x|x2+x=0}={-1,0},则N?M,故选B.
答案:B
3.(2010·广东卷)若集合A={0,1,2,3},B={1,2,4},则集合A∪B=
( )
A.{0,1,2,3,4}
B.{1,2,3,4,}
C.{1,2}
D.{0}
答案:A
4.(2010·山东卷)已知全集U=R,集合M={x|x2-4≤0}则?UM=
( )
A.{x|-2<x<2}
B.{x|-2≤x≤2}
C.{x|x<-2或x>2}
D.{x|x≤-2或x≥2}
解析:M={x|x2-4≤0}={x|-2≤x≤2}∴?UM={x|x<-2或x>2}.
答案:C
5.已知集合A={-1,3,m},集合B={3,4},若B?A,则实数m=________.
解析:∵B?A,∴4∈B?4∈A?m=4.
答案:4
考向一 集合的基本概念
考向二 集合间的基本关系
反思感悟:善于总结,养成习惯
对于含有参数的问题,求解的基本策略是分类讨论,在分类讨论时要把字母参数的各种可能情况都考虑进去,特别注意不要遗漏了参数等于零的情况.
迁移发散
2.已知集合A={x|x2-3x-10≤0},
(1)若B?A,B={x|m+1≤x≤2m-1},求实数m的取值范围;
(2)若A?B,B={x|m-6≤x≤2m-1},求实数m的取值范围;
(3)若A=B,B={x|m-6≤x≤2m-1},求实数m的取值范围.
解:(1)由A={x|x2-3x-10≤0},得
A={x|-2≤x≤5},
∵B?A,∴①若B=?,
则m+1>2m-1,
即m<2,此时满足B?A.
考向三 集合的基本运算
反思感悟:善于总结,养成习惯
1.求一个集合在指定集合中的补集,其一般方法是把这个集合法求出来,再根
据补集的含义求解
2.在解对数不等式时一定要注意对数函数的定义域本身对变量的限制条件,不
然就会扩大解的范围,同时注意对数函数性质的应用,把对数不等式转化为
一般的代数不等式.
迁移发散
3.设集合A={x|0≤x≤4},B={y|y=-x2,-1≤x≤2},则?R(A∩B)
等于
( )
A.R
B.{x|x∈R,x≠0}
C.{0}
D.?
解析:B={y|y=-x2,-1≤x≤2}=[-4,0],则A∩B={0},∴?R(A∩B)
={x|x∈R,x≠0}.
答案:B
课堂总结
感悟提升
1.集合中的元素的三个性质,特别是无序性和互异性在解题时经常用到.解题
后要进行检验,要重视符号语言与文字语言之间的相互转化.
2.空集在解题时有特殊地位,它是任何集合的子集,是任何非空集合的真子
集,时刻关注对空集的讨论,防止漏掉.
3.解题时注意区分两大关系:一是元素与集合的从属关系;二是集合与集合的
包含关系.
4.解答集合题目,认清集合元素的属性(是点集、数集或其他情形)和化简集合
是正确求解的两个先决条件.
5.韦恩图示法和数轴图示法是进行集合交、并、补运算的常用方法,其中运用
数轴图示法要特别注意端点是实心点还是空心点.
