高中物理必修二6.1 圆周运动(课件)(19张PPT)
文档属性
| 名称 | 高中物理必修二6.1 圆周运动(课件)(19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 781.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-09-08 05:52:14 | ||
图片预览





文档简介
(共19张PPT)
质点的运动轨迹是圆(圆的一部分)
的运动叫做圆周运动
-、匀速圆周运动
——物体沿着圆周运动,并且线速度的大小处处相等,这种运动叫做匀速圆周运动。
匀速圆周运动中的“匀速”指速度不变吗?
注意:“匀速”圆周运动是一种变速曲线运动
速度方向时刻在变化
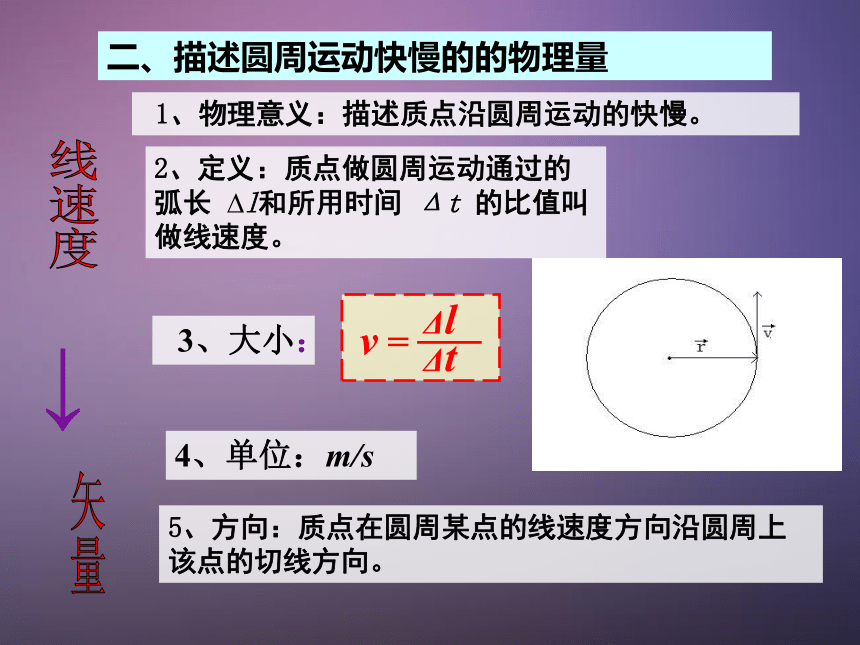
二、描述圆周运动快慢的的物理量
1、物理意义:描述质点沿圆周运动的快慢。
2、定义:质点做圆周运动通过的弧长
?l和所用时间
Δt
的比值叫做线速度。
3、大小:
4、单位:m/s
v
=
Δt
Δl
5、方向:质点在圆周某点的线速度方向沿圆周上该点的切线方向。
↓
1、物理意义:描述质点转过圆心角的快慢。
2、定义:质点所在的半径转过圆心角Δθ和所用时间Δt的比值叫做角速度。
3、大小:
ω=
Δt
Δ
θ
Δ
θ
4、角速度的单位:
弧度/秒
rad/s
注意:匀速圆周运动是角速度不变的运动,但线速度
是变化的(线速度的方向不断变化)。
3、周期、频率、转速
匀速圆周运动是一种周期性的运动。所谓周期性,是指运动物体经过一定的时间后,又重复回到原来的位置,瞬时速度也重复回到原来的大小和方向。
周期:运动物体完成一次周期性的运动所用的时间
。用T
表示。单位:秒(s)
频率:单位时间内完成的周期次数。用
f
表示,
即
f
=
1/T
。单位:赫兹(Hz)或s-1
转速:单位时间内转过的圈数。用
n
表示。
单位:转每秒,符号r/s
;
转每分,符号r/min。
频率和周期是互为倒数的关系。
三、线速度、角速度、周期、频率、转速间的关系
?
=
ω
r
?
=
2πr
T
ω
=
2π
T
﹜
得
ω
=
2π
T
=
2πn
=2πf
讨论:
1)r一定,v与ω成正比
2)v一定,ω与r成反比
3)ω一定,v与r成正比
1)传动装置线速度的关系
a、皮带传动-线速度相等
b、齿轮传动-线速度相等
同一传动各轮边缘上线速度相同
四、两个重要的结论
A
B
C
2)同一轮上各点的角速度关系
同一轮上各点的角速度相同
圆周运动的传动装置问题
C
B
A
B
A
C
如图所示装置中,A、B、C三个轮的半径分别为r、2r、3r,求:
⑴图中A、B两点的线速度之比
(2)A、B两点的角速度之比
(3)A、C两点的角速度之比
(4)A、C两点的线速度之比
(1)A、B的线速度相同
(3)A、C的角速度相同
(2)由?
=ωr
得
(4)由?
=ωr
得
常见传动从动装置
皮带传动
齿轮传动
c
A
B
摩擦传动
皮带(链条、齿轮、摩擦等)传动,轮边缘的质点线速度大小相等。
C
B
A
1、关于匀速圆周运动的说法正确的是(
)
A、线速度不变的运动
B、角速度、速率、转速不变的运动
C、匀速圆周运动是变速运动
D、质点做匀速圆周运动时处于平衡状态
课堂巩固练习
BC
2、如图所示,主动轮P和从动轮Q的半径之比为2:1,A、B两点分别在两轮边缘上,则A、B两点的线速度大小之比为VA:VB=________,角速度大小之比为ωA:
ωB=________
1:1
1:2
1.线速度
(1)物理意义:描述质点沿圆周运动的快慢。
(2)定义:质点做圆周运动通过的弧长△s和所用时间△t的比值叫做线速度。(比值定义法,这里是弧长,而直线运动中是位移)
(3)大小:v=△l/△t单位:m/s(s是弧长。非位移)。
(4)当选取的时间△t很小很小时(趋近零)。弧长△s就等于物体在t时刻的位移,定义式中的v,就是直线运动中学过的瞬时速度了。
(5)方向;在圆周各点的切线上。
2.角速度
(1)物理意义:描述质点转过的圆心角的快慢。
(2)定义:在匀速圆周运动中。连接运动质点和圆心的半径转过△θ的角度跟所用时间△t的比值,就是质点运动的角速度。
(3)定义式:ω=△θ/△t
(4)单位:弧度/秒(rad/s)
。
课堂小结
4.线速度与角速度的关系
5.周期、频率、转速
(1).匀速圆周运动是一种周期性的运动。所谓周期性,是指运动物体经过一定的时间后,又重复回到原来的位置,瞬时速度也重复回到原来的大小和方向。
周期:运动物体完成一次周期性的运动所用的时间
。用T
表示。单位:秒(s)
(2)
频率:单位时间内完成的周期次数。用
f
表示,
即
f
=
1/T
。单位:赫兹(Hz)或s-1
频率和周期是互为倒数的关系。
(3)转速:单位时间内转过的圈数。用
n
表示。
单位:转每秒,符号r/s
;
转每分,符号r/min
质点的运动轨迹是圆(圆的一部分)
的运动叫做圆周运动
-、匀速圆周运动
——物体沿着圆周运动,并且线速度的大小处处相等,这种运动叫做匀速圆周运动。
匀速圆周运动中的“匀速”指速度不变吗?
注意:“匀速”圆周运动是一种变速曲线运动
速度方向时刻在变化
二、描述圆周运动快慢的的物理量
1、物理意义:描述质点沿圆周运动的快慢。
2、定义:质点做圆周运动通过的弧长
?l和所用时间
Δt
的比值叫做线速度。
3、大小:
4、单位:m/s
v
=
Δt
Δl
5、方向:质点在圆周某点的线速度方向沿圆周上该点的切线方向。
↓
1、物理意义:描述质点转过圆心角的快慢。
2、定义:质点所在的半径转过圆心角Δθ和所用时间Δt的比值叫做角速度。
3、大小:
ω=
Δt
Δ
θ
Δ
θ
4、角速度的单位:
弧度/秒
rad/s
注意:匀速圆周运动是角速度不变的运动,但线速度
是变化的(线速度的方向不断变化)。
3、周期、频率、转速
匀速圆周运动是一种周期性的运动。所谓周期性,是指运动物体经过一定的时间后,又重复回到原来的位置,瞬时速度也重复回到原来的大小和方向。
周期:运动物体完成一次周期性的运动所用的时间
。用T
表示。单位:秒(s)
频率:单位时间内完成的周期次数。用
f
表示,
即
f
=
1/T
。单位:赫兹(Hz)或s-1
转速:单位时间内转过的圈数。用
n
表示。
单位:转每秒,符号r/s
;
转每分,符号r/min。
频率和周期是互为倒数的关系。
三、线速度、角速度、周期、频率、转速间的关系
?
=
ω
r
?
=
2πr
T
ω
=
2π
T
﹜
得
ω
=
2π
T
=
2πn
=2πf
讨论:
1)r一定,v与ω成正比
2)v一定,ω与r成反比
3)ω一定,v与r成正比
1)传动装置线速度的关系
a、皮带传动-线速度相等
b、齿轮传动-线速度相等
同一传动各轮边缘上线速度相同
四、两个重要的结论
A
B
C
2)同一轮上各点的角速度关系
同一轮上各点的角速度相同
圆周运动的传动装置问题
C
B
A
B
A
C
如图所示装置中,A、B、C三个轮的半径分别为r、2r、3r,求:
⑴图中A、B两点的线速度之比
(2)A、B两点的角速度之比
(3)A、C两点的角速度之比
(4)A、C两点的线速度之比
(1)A、B的线速度相同
(3)A、C的角速度相同
(2)由?
=ωr
得
(4)由?
=ωr
得
常见传动从动装置
皮带传动
齿轮传动
c
A
B
摩擦传动
皮带(链条、齿轮、摩擦等)传动,轮边缘的质点线速度大小相等。
C
B
A
1、关于匀速圆周运动的说法正确的是(
)
A、线速度不变的运动
B、角速度、速率、转速不变的运动
C、匀速圆周运动是变速运动
D、质点做匀速圆周运动时处于平衡状态
课堂巩固练习
BC
2、如图所示,主动轮P和从动轮Q的半径之比为2:1,A、B两点分别在两轮边缘上,则A、B两点的线速度大小之比为VA:VB=________,角速度大小之比为ωA:
ωB=________
1:1
1:2
1.线速度
(1)物理意义:描述质点沿圆周运动的快慢。
(2)定义:质点做圆周运动通过的弧长△s和所用时间△t的比值叫做线速度。(比值定义法,这里是弧长,而直线运动中是位移)
(3)大小:v=△l/△t单位:m/s(s是弧长。非位移)。
(4)当选取的时间△t很小很小时(趋近零)。弧长△s就等于物体在t时刻的位移,定义式中的v,就是直线运动中学过的瞬时速度了。
(5)方向;在圆周各点的切线上。
2.角速度
(1)物理意义:描述质点转过的圆心角的快慢。
(2)定义:在匀速圆周运动中。连接运动质点和圆心的半径转过△θ的角度跟所用时间△t的比值,就是质点运动的角速度。
(3)定义式:ω=△θ/△t
(4)单位:弧度/秒(rad/s)
。
课堂小结
4.线速度与角速度的关系
5.周期、频率、转速
(1).匀速圆周运动是一种周期性的运动。所谓周期性,是指运动物体经过一定的时间后,又重复回到原来的位置,瞬时速度也重复回到原来的大小和方向。
周期:运动物体完成一次周期性的运动所用的时间
。用T
表示。单位:秒(s)
(2)
频率:单位时间内完成的周期次数。用
f
表示,
即
f
=
1/T
。单位:赫兹(Hz)或s-1
频率和周期是互为倒数的关系。
(3)转速:单位时间内转过的圈数。用
n
表示。
单位:转每秒,符号r/s
;
转每分,符号r/min
