高中物理必修二6.4 生活中的圆周运动(课件)(38张PPT)
文档属性
| 名称 | 高中物理必修二6.4 生活中的圆周运动(课件)(38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-09-08 06:03:58 | ||
图片预览







文档简介
(共38张PPT)
第五章
曲线运动
第七节生活中的圆周运动
1、什么是向心力?其作用是什么?
一、知识回顾
提供物体做圆周运动的力
(受力分析)
物体做圆周运动所需的力
(运动分析)
二、火车转弯
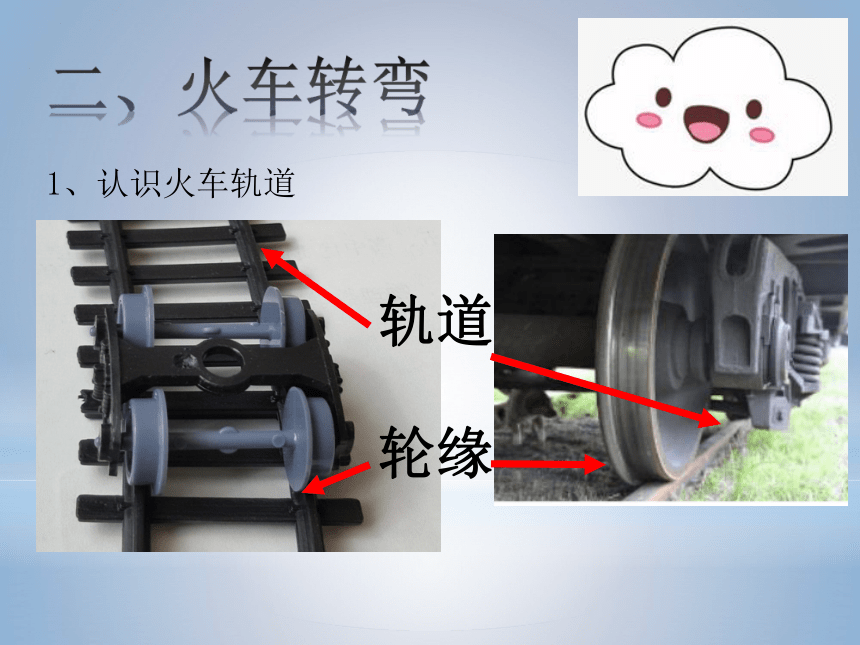
1、认识火车轨道
轮缘
轨道
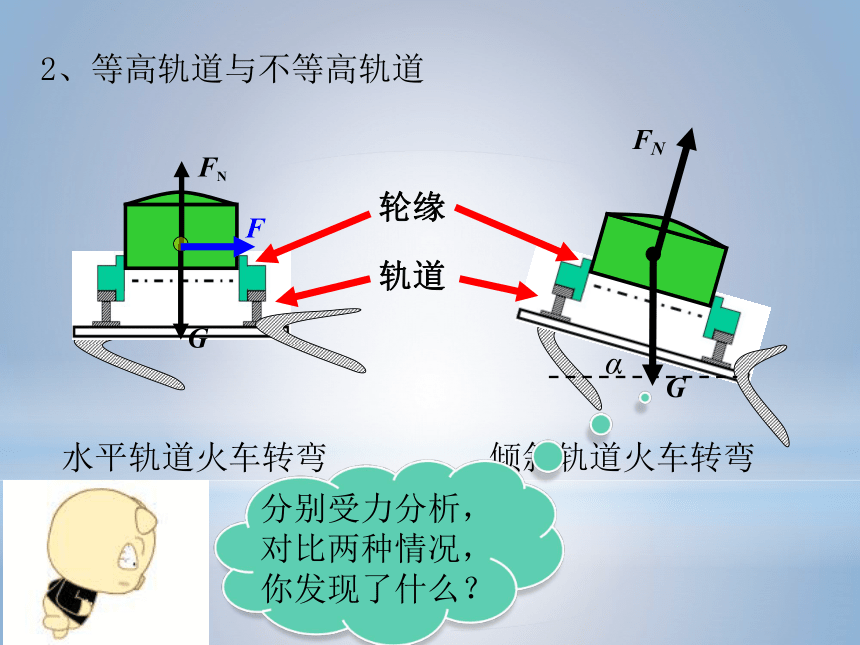
2、等高轨道与不等高轨道
FN
F
G
轮缘
轨道
FN
G
α
水平轨道火车转弯
倾斜轨道火车转弯
分别受力分析,对比两种情况,你发现了什么?
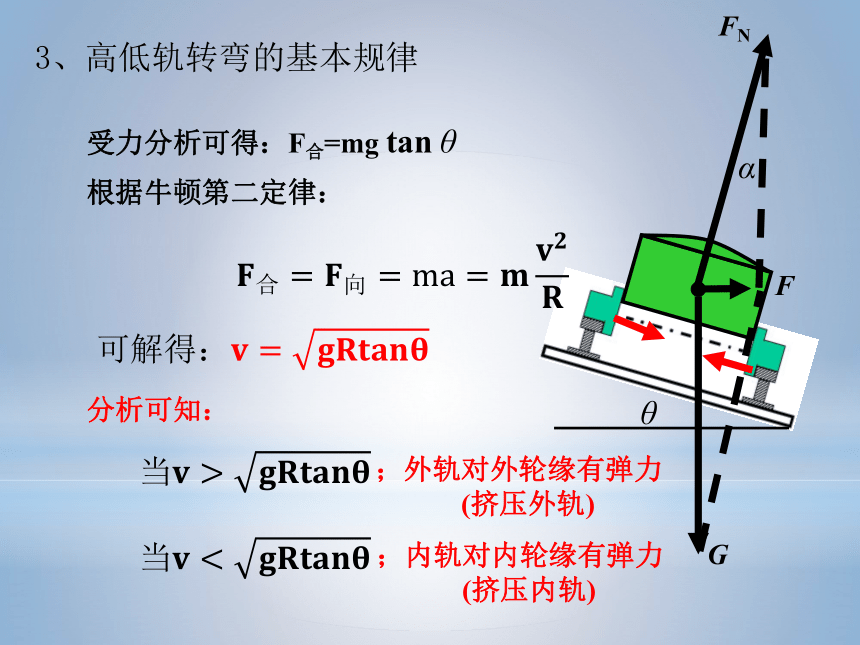
3、高低轨转弯的基本规律
根据牛顿第二定律:
FN
G
F
θ
α
受力分析可得:F合=mg
tan
θ
;外轨对外轮缘有弹力
(挤压外轨)
;内轨对内轮缘有弹力
(挤压内轨)
分析可知:
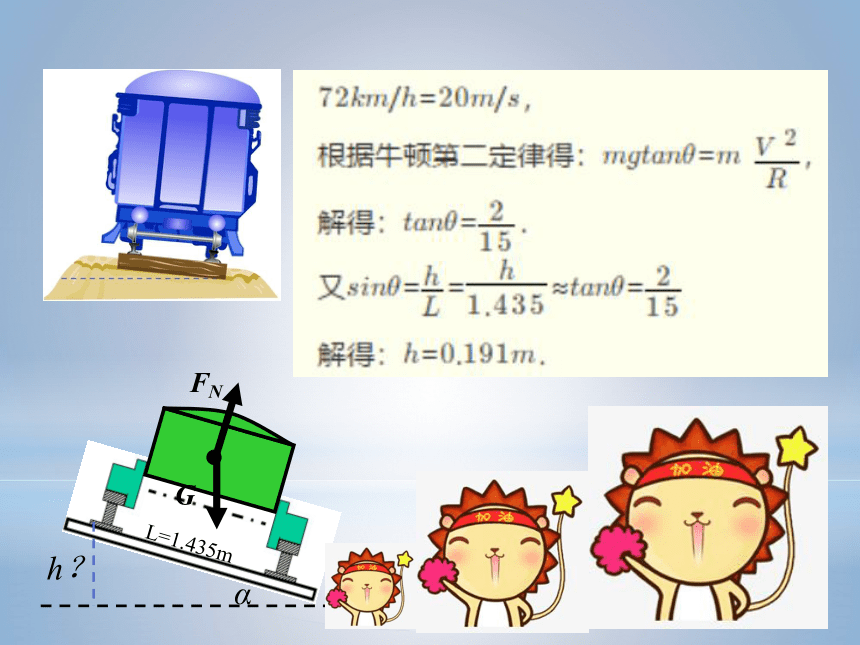
例1、铁路转弯处的圆弧半径是300m,轨距是1.435m,规定火车通过这里的速度是72km/h。g=10m/s2,当α很小时,tanα=sinα。
(1)内外轨的高度差应该是多大,才能使铁轨不受轮缘的挤压?
(2)保持内外轨的这个高度差,如果车的速度大于或小于72km/h,会分别发生什么现象?说明理由。
FN
G
α
L=1.435m
h?
例2、在修筑铁路时,弯道处的外轨会略高于内轨(如图),当火车以规定的行驶速度转弯时,内、外轨均不会受到轮缘的挤压,设此时的速度大小为v,重力加速度为g,以下说法中正确的是( )
A.该弯道的半径R=v2/r
B.当火车质量改变时,规定的行驶速度也将改变
C.当火车速率大于v时,外轨将受到轮缘的挤压
D.当火车速率小于v时,外轨将受到轮缘的挤压
C
二、汽车转弯
1、平地转弯与山路转弯
A、平地转弯
Ff
G
N
Ff
分析可知,此时车轮与地面的摩擦力提供向心力。
=μmg
为安全行驶:可采取哪些措施?
①增大动摩擦因数μ
②增大转弯半径
③使路面倾斜
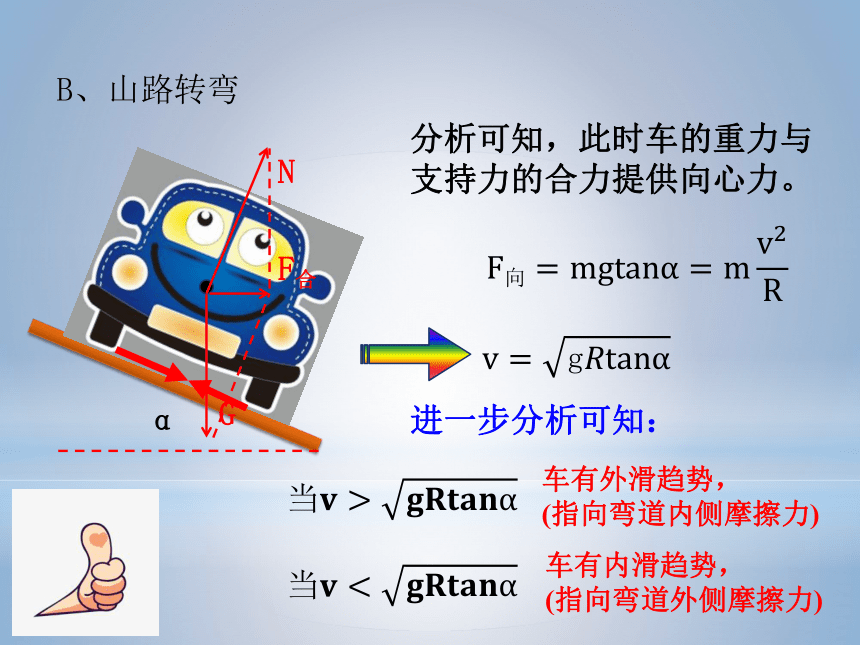
B、山路转弯
F合
G
N
分析可知,此时车的重力与支持力的合力提供向心力。
α
车有外滑趋势,
(指向弯道内侧摩擦力)
车有内滑趋势,
(指向弯道外侧摩擦力)
进一步分析可知:
例3、摩托赛车在水平路面上转弯,地面的摩擦力已达到最大,当摩托赛车的速率增为原来的2倍时,则摩托赛车转弯的轨道半径必须(
)
A、至少增大到原来的4倍
B、至少增大到原来的2倍
C、至少增大到原来的√2倍
D、减小到原来的1/2
A
例4、公路急转弯处通常是交通事故多发地带。如图,某公路急转弯处是一圆弧,当汽车行驶的速率为v0时,汽车恰好没有向公路内外两侧滑动的趋势。则在该弯道处(
)
A.
路面外侧低内侧高
B.
车速只要低于v0,车辆便会向内侧滑动
C.
当路面结冰时,与未结冰时相比,v0的值变小
D.
车速虽然高于v0,但只要不超出某一最高限度,车辆便不会向外侧滑动
D
例5、水平路面汽车转弯靠静摩擦力充当向心力,由于静摩擦力有个最大值,所以,在转弯半径r一定的情况下,转弯的速度v0不能太大,我们可以在转弯处设计成倾角为θ的坡路,如图所示,在动摩擦因数μ不变的情况下,且μ)
A.
汽车在水平路面转弯,汽车的质量越大,转弯允许的最大速度越大
B.
汽车在倾斜路面转弯,随速度的增大,受到的摩擦力增大
C.
汽车恰好能停在倾角为θ的倾斜路面上
D.
汽车在倾斜路面转弯,若沿倾斜路面方向没有侧滑运动趋势,则速度v0=√grtanθ
D
1、定义:做匀速圆周运动的物体,在一定条件下,做逐渐远离圆心的运动,这种运动叫离心运动。
三、离心运动
2、原因:向心力突然消失或者合外力不足于提供向心力。
3、合外力超过所需向心力,物体做逐渐靠近圆心的运动,即向心运动(近心运动)。
4、生活现象
例6、下列关于离心现象的说法正确的是(
)
A.
做匀速圆周运动的物体,当它所受的一切力都突然消失时,它将沿切线做直线运动
B.
当物体所受的离心力大于向心力时产生离心现象
C.
做匀速圆周运动的物体,当它所受的一切力都消失时,它将做背离圆心的圆周运动
D.
做匀速圆周运动的物体,当它所受的一切力都突然消失时,它将做曲线运动
A
例7、如图,光滑水平面上,小球m在拉力F作用下做匀速圆周运动,若小球运动到P点时,拉力F突然减小为F2,关于小球运动情况的说法正确的是(?)
A.
小球在离心力作用下将沿轨迹Pa做离心运动
B.
小球在离心力作用下将沿轨迹Pb做离心运动
C.
小球在离心力作用下将沿轨迹Pc做离心运动
D.
小球将沿轨迹Pb做离心运动,但不受离心力
D
四、汽车过桥
1、凸形桥
对车受力分析有:
G
N
由牛顿第二定律:
由上式,当速度v增加时,支持力N减小
当N=0时,
即说明当车过凸形桥时,车容易“飘”
2、凸形桥
对车受力分析有:
G
N
由牛顿第二定律:
由上式,当速度v增加时,支持力N增加
当N=Nm时,
即说明当车过凹形桥时,车容易“爆胎”
例8、质量为m
的汽车以速率v通过半径为R的拱桥,如图所示,求汽车在桥顶时对路面的压力是多大?
解:汽车通过桥顶时,受力如图:
mg
FN
O
R
由牛顿第二定律:
由牛顿第三定律:
失重
完全失重
当:
例9、地球可以看做一个巨大的拱形桥,桥面的半径就是地球的半径。会不会出现这样的情况:速度大到一定程度时,地面对车的支持力为零?这时驾驶员与座椅之间的压力是多少……
第一宇宙速度
思考:航天员在航天器中绕地球做匀速圆周运动时,航天员处于完全的失重状态,航天员是否不受地球引力?
mg
FN
由牛顿第二定律:
当FN=0时,
此时座舱对航天员的支持力FN=0,
航天员处于失重状态
例10、(多)宇宙飞船绕地球做匀速圆周运动,下列说法中正确的有(
)
A.在飞船内可以用天平测量物体的质量
B.在飞船内可以用水银气压计测舱内的气压
C.在飞船内可以用弹簧测力计测拉力
D.在飞船内将重物挂于弹簧测力计上,弹簧测力计示数为0,但重物仍受地球的引力
CD
五、杆模型与绳模型
1、轻绳模型
mg
F
受力分析如图:
由牛顿第二定律可得:
当v减小时,拉力F减小,
临界当F=0时,v取得最小值
绳模型(水流星),经过最高点v的速度不小于
2、单环模型
mg
F
同理由:
可得
若v小于临界速度,将出现脱轨现象
例11、(多选)用细绳拴着质量为m的小球,在竖直平面内做半径为R的圆周运动,如图所示.则下列说法正确的是(
)
A.小球通过最高点时,绳子张力可以为0
B.小球通过最高点时的最小速度为0
C.小球刚好通过最高点时的速度是
D.小球通过最高点时,绳子对小球的作用力可以与球所受重力方向相反
AC
例12、如图,在竖直平面内有一半径为R的半圆形轨道,最高点为P点,现让一小滑块(可视为质点)从水平地面上向半圆形轨道运动,下列关于小滑块运动情况的分析,正确的是(
)
D
A.若vP=0,小滑块恰能通过P点,且离开P点后做自由落体运动
B.若vP=0,小滑块能通过P点,且离开P点后做平抛运动
C.若vP=
,小滑块恰能到达P点,且离开P点后做自由落体运动
D.若vP=
,小滑块恰能到达P点,且离开P点后做平抛运动
例13、(多)英国特技演员史蒂夫·特鲁加里亚曾飞车挑战世界最大环形车道.如图所示,环形车道竖直放置,直径达12
m.若汽车在车道上以12
m/s恒定的速率运动,演员与汽车的总质量为1
000
kg,重力加速度g取10
m/s2,则(
)
A.汽车通过最低点时,演员处于超重状态
B.汽车通过最高点时对环形车道的压力为1.4×104
N
C.若要挑战成功,汽车不可能以低于12
m/s的恒定速率运动
D.汽车在环形车道上的角速度为1
rad/s
选AB.
AB
3、轻杆模型
假设杆与物块恰好无作用力:受力分析如图:
由牛顿第二定律可得:
得:
mg
①当v增加时,所需向心力变大,重力不足于提供向心力,杆提供向下的拉力。
②当v减小时,所需向心力变小,重力超过所需向心力,杆提供向上的支持力。
(1)当v=0时,FN=mg,FN为支持力,沿半径背离圆心。
(2)当0,FN背离圆心,随v的增大而减小
(3)当v=时,FN=0
(4)当v>时,FN+mg=m
,
FN指向圆心,随v的增大而增大
4、双环模型
mg
mg
N
①在最高点分析,球可能受到向上的支持力,也可能受到向下的支持力,还可能不受支持力。
②在最低点分析,球肯定受到向上的支持力
例14、(多)
一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球在竖直面内做半径为R的圆周运动,如图所示,则下列说法错误的是(
)
A.小球过最高点时,杆所受到的弹力可以等于零
B.小球过最高点的最小速度是零
C.小球过最高点时,杆对球的作用力一定随速度增大而增大
D.小球过最高点时,杆对球的作用力一定随速度增大而减小
CD
例15、(多)如图,长0.5m的轻质细杆,一端固定有一个质量为3kg的小球,另一端由电动机带动,使杆绕O点在竖直平面内做匀速圆周运动,小球的速率为2m/s,取重力加速度g=10m/s2,下列说法正确的是(
)
A.小球通过最高点时,对杆的拉力大小是24N
B.小球通过最高点时,对杆的压力大小是6N
C.小球通过最低点时,对杆的拉力大小是54N
D.小球通过最低点时,对杆的拉力大小是24N
BC
例16、(多)宇航员在绕地球匀速运行的空间站做实验.如图,光滑的半圆形管道和底部粗糙的水平AB管道相连接,整个装置安置在竖直平面上,宇航员让一小球(直径比管道直径小)以一定的速度从A端射入,小球通过AB段并越过半圆形管道最高点C后飞出,则(
)
A.小球从C点飞出后将做平抛运动
B.小球在AB管道运动时不受摩擦力作用
C.小球在半圆管道运动时受力平衡
D.小球在半圆管道运动时对管道有压力
BD
例17、如图所示,质量为m的小球在竖直放置的光滑圆形管道内做圆周运动,ab是过轨道圆心的水平线,下列说法中正确的是(
)
A.小球在ab线上方管道中运动时,内侧管壁对小球一定有作用力
B.小球在ab线上方管道中运动时,外侧管壁对小球一定有作用力
C.小球在ab线下方管道中运动时,内侧管壁对小球一定有作用力
D.小球在ab线下方管道中运动时,外侧管壁对小球一定有作用力
D
第五章
曲线运动
第七节生活中的圆周运动
1、什么是向心力?其作用是什么?
一、知识回顾
提供物体做圆周运动的力
(受力分析)
物体做圆周运动所需的力
(运动分析)
二、火车转弯
1、认识火车轨道
轮缘
轨道
2、等高轨道与不等高轨道
FN
F
G
轮缘
轨道
FN
G
α
水平轨道火车转弯
倾斜轨道火车转弯
分别受力分析,对比两种情况,你发现了什么?
3、高低轨转弯的基本规律
根据牛顿第二定律:
FN
G
F
θ
α
受力分析可得:F合=mg
tan
θ
;外轨对外轮缘有弹力
(挤压外轨)
;内轨对内轮缘有弹力
(挤压内轨)
分析可知:
例1、铁路转弯处的圆弧半径是300m,轨距是1.435m,规定火车通过这里的速度是72km/h。g=10m/s2,当α很小时,tanα=sinα。
(1)内外轨的高度差应该是多大,才能使铁轨不受轮缘的挤压?
(2)保持内外轨的这个高度差,如果车的速度大于或小于72km/h,会分别发生什么现象?说明理由。
FN
G
α
L=1.435m
h?
例2、在修筑铁路时,弯道处的外轨会略高于内轨(如图),当火车以规定的行驶速度转弯时,内、外轨均不会受到轮缘的挤压,设此时的速度大小为v,重力加速度为g,以下说法中正确的是( )
A.该弯道的半径R=v2/r
B.当火车质量改变时,规定的行驶速度也将改变
C.当火车速率大于v时,外轨将受到轮缘的挤压
D.当火车速率小于v时,外轨将受到轮缘的挤压
C
二、汽车转弯
1、平地转弯与山路转弯
A、平地转弯
Ff
G
N
Ff
分析可知,此时车轮与地面的摩擦力提供向心力。
=μmg
为安全行驶:可采取哪些措施?
①增大动摩擦因数μ
②增大转弯半径
③使路面倾斜
B、山路转弯
F合
G
N
分析可知,此时车的重力与支持力的合力提供向心力。
α
车有外滑趋势,
(指向弯道内侧摩擦力)
车有内滑趋势,
(指向弯道外侧摩擦力)
进一步分析可知:
例3、摩托赛车在水平路面上转弯,地面的摩擦力已达到最大,当摩托赛车的速率增为原来的2倍时,则摩托赛车转弯的轨道半径必须(
)
A、至少增大到原来的4倍
B、至少增大到原来的2倍
C、至少增大到原来的√2倍
D、减小到原来的1/2
A
例4、公路急转弯处通常是交通事故多发地带。如图,某公路急转弯处是一圆弧,当汽车行驶的速率为v0时,汽车恰好没有向公路内外两侧滑动的趋势。则在该弯道处(
)
A.
路面外侧低内侧高
B.
车速只要低于v0,车辆便会向内侧滑动
C.
当路面结冰时,与未结冰时相比,v0的值变小
D.
车速虽然高于v0,但只要不超出某一最高限度,车辆便不会向外侧滑动
D
例5、水平路面汽车转弯靠静摩擦力充当向心力,由于静摩擦力有个最大值,所以,在转弯半径r一定的情况下,转弯的速度v0不能太大,我们可以在转弯处设计成倾角为θ的坡路,如图所示,在动摩擦因数μ不变的情况下,且μ
A.
汽车在水平路面转弯,汽车的质量越大,转弯允许的最大速度越大
B.
汽车在倾斜路面转弯,随速度的增大,受到的摩擦力增大
C.
汽车恰好能停在倾角为θ的倾斜路面上
D.
汽车在倾斜路面转弯,若沿倾斜路面方向没有侧滑运动趋势,则速度v0=√grtanθ
D
1、定义:做匀速圆周运动的物体,在一定条件下,做逐渐远离圆心的运动,这种运动叫离心运动。
三、离心运动
2、原因:向心力突然消失或者合外力不足于提供向心力。
3、合外力超过所需向心力,物体做逐渐靠近圆心的运动,即向心运动(近心运动)。
4、生活现象
例6、下列关于离心现象的说法正确的是(
)
A.
做匀速圆周运动的物体,当它所受的一切力都突然消失时,它将沿切线做直线运动
B.
当物体所受的离心力大于向心力时产生离心现象
C.
做匀速圆周运动的物体,当它所受的一切力都消失时,它将做背离圆心的圆周运动
D.
做匀速圆周运动的物体,当它所受的一切力都突然消失时,它将做曲线运动
A
例7、如图,光滑水平面上,小球m在拉力F作用下做匀速圆周运动,若小球运动到P点时,拉力F突然减小为F2,关于小球运动情况的说法正确的是(?)
A.
小球在离心力作用下将沿轨迹Pa做离心运动
B.
小球在离心力作用下将沿轨迹Pb做离心运动
C.
小球在离心力作用下将沿轨迹Pc做离心运动
D.
小球将沿轨迹Pb做离心运动,但不受离心力
D
四、汽车过桥
1、凸形桥
对车受力分析有:
G
N
由牛顿第二定律:
由上式,当速度v增加时,支持力N减小
当N=0时,
即说明当车过凸形桥时,车容易“飘”
2、凸形桥
对车受力分析有:
G
N
由牛顿第二定律:
由上式,当速度v增加时,支持力N增加
当N=Nm时,
即说明当车过凹形桥时,车容易“爆胎”
例8、质量为m
的汽车以速率v通过半径为R的拱桥,如图所示,求汽车在桥顶时对路面的压力是多大?
解:汽车通过桥顶时,受力如图:
mg
FN
O
R
由牛顿第二定律:
由牛顿第三定律:
失重
完全失重
当:
例9、地球可以看做一个巨大的拱形桥,桥面的半径就是地球的半径。会不会出现这样的情况:速度大到一定程度时,地面对车的支持力为零?这时驾驶员与座椅之间的压力是多少……
第一宇宙速度
思考:航天员在航天器中绕地球做匀速圆周运动时,航天员处于完全的失重状态,航天员是否不受地球引力?
mg
FN
由牛顿第二定律:
当FN=0时,
此时座舱对航天员的支持力FN=0,
航天员处于失重状态
例10、(多)宇宙飞船绕地球做匀速圆周运动,下列说法中正确的有(
)
A.在飞船内可以用天平测量物体的质量
B.在飞船内可以用水银气压计测舱内的气压
C.在飞船内可以用弹簧测力计测拉力
D.在飞船内将重物挂于弹簧测力计上,弹簧测力计示数为0,但重物仍受地球的引力
CD
五、杆模型与绳模型
1、轻绳模型
mg
F
受力分析如图:
由牛顿第二定律可得:
当v减小时,拉力F减小,
临界当F=0时,v取得最小值
绳模型(水流星),经过最高点v的速度不小于
2、单环模型
mg
F
同理由:
可得
若v小于临界速度,将出现脱轨现象
例11、(多选)用细绳拴着质量为m的小球,在竖直平面内做半径为R的圆周运动,如图所示.则下列说法正确的是(
)
A.小球通过最高点时,绳子张力可以为0
B.小球通过最高点时的最小速度为0
C.小球刚好通过最高点时的速度是
D.小球通过最高点时,绳子对小球的作用力可以与球所受重力方向相反
AC
例12、如图,在竖直平面内有一半径为R的半圆形轨道,最高点为P点,现让一小滑块(可视为质点)从水平地面上向半圆形轨道运动,下列关于小滑块运动情况的分析,正确的是(
)
D
A.若vP=0,小滑块恰能通过P点,且离开P点后做自由落体运动
B.若vP=0,小滑块能通过P点,且离开P点后做平抛运动
C.若vP=
,小滑块恰能到达P点,且离开P点后做自由落体运动
D.若vP=
,小滑块恰能到达P点,且离开P点后做平抛运动
例13、(多)英国特技演员史蒂夫·特鲁加里亚曾飞车挑战世界最大环形车道.如图所示,环形车道竖直放置,直径达12
m.若汽车在车道上以12
m/s恒定的速率运动,演员与汽车的总质量为1
000
kg,重力加速度g取10
m/s2,则(
)
A.汽车通过最低点时,演员处于超重状态
B.汽车通过最高点时对环形车道的压力为1.4×104
N
C.若要挑战成功,汽车不可能以低于12
m/s的恒定速率运动
D.汽车在环形车道上的角速度为1
rad/s
选AB.
AB
3、轻杆模型
假设杆与物块恰好无作用力:受力分析如图:
由牛顿第二定律可得:
得:
mg
①当v增加时,所需向心力变大,重力不足于提供向心力,杆提供向下的拉力。
②当v减小时,所需向心力变小,重力超过所需向心力,杆提供向上的支持力。
(1)当v=0时,FN=mg,FN为支持力,沿半径背离圆心。
(2)当0
(3)当v=时,FN=0
(4)当v>时,FN+mg=m
,
FN指向圆心,随v的增大而增大
4、双环模型
mg
mg
N
①在最高点分析,球可能受到向上的支持力,也可能受到向下的支持力,还可能不受支持力。
②在最低点分析,球肯定受到向上的支持力
例14、(多)
一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球在竖直面内做半径为R的圆周运动,如图所示,则下列说法错误的是(
)
A.小球过最高点时,杆所受到的弹力可以等于零
B.小球过最高点的最小速度是零
C.小球过最高点时,杆对球的作用力一定随速度增大而增大
D.小球过最高点时,杆对球的作用力一定随速度增大而减小
CD
例15、(多)如图,长0.5m的轻质细杆,一端固定有一个质量为3kg的小球,另一端由电动机带动,使杆绕O点在竖直平面内做匀速圆周运动,小球的速率为2m/s,取重力加速度g=10m/s2,下列说法正确的是(
)
A.小球通过最高点时,对杆的拉力大小是24N
B.小球通过最高点时,对杆的压力大小是6N
C.小球通过最低点时,对杆的拉力大小是54N
D.小球通过最低点时,对杆的拉力大小是24N
BC
例16、(多)宇航员在绕地球匀速运行的空间站做实验.如图,光滑的半圆形管道和底部粗糙的水平AB管道相连接,整个装置安置在竖直平面上,宇航员让一小球(直径比管道直径小)以一定的速度从A端射入,小球通过AB段并越过半圆形管道最高点C后飞出,则(
)
A.小球从C点飞出后将做平抛运动
B.小球在AB管道运动时不受摩擦力作用
C.小球在半圆管道运动时受力平衡
D.小球在半圆管道运动时对管道有压力
BD
例17、如图所示,质量为m的小球在竖直放置的光滑圆形管道内做圆周运动,ab是过轨道圆心的水平线,下列说法中正确的是(
)
A.小球在ab线上方管道中运动时,内侧管壁对小球一定有作用力
B.小球在ab线上方管道中运动时,外侧管壁对小球一定有作用力
C.小球在ab线下方管道中运动时,内侧管壁对小球一定有作用力
D.小球在ab线下方管道中运动时,外侧管壁对小球一定有作用力
D
