17.3勾股定理 课件 冀教版数学八年级上册(1)(共23张ppt)
文档属性
| 名称 | 17.3勾股定理 课件 冀教版数学八年级上册(1)(共23张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 10:55:39 | ||
图片预览


文档简介
(共23张PPT)
第十七章
冀教版初中数学八年级上册
17.3
勾股定理
毕达哥拉斯
(公元前572-前492年)
古希腊著名的哲学家
数学家。
情境引入
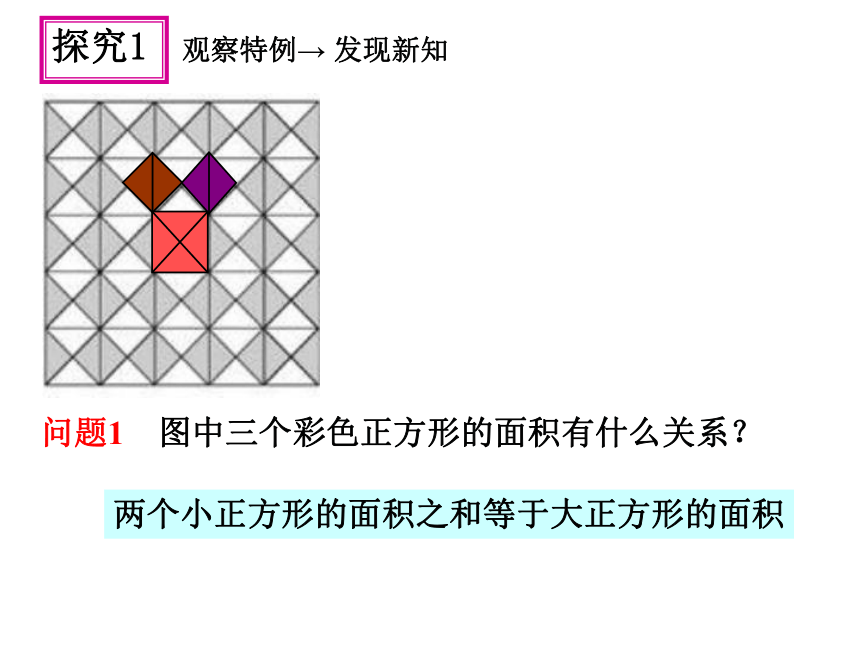
问题1 图中三个彩色正方形的面积有什么关系?
探究1
观察特例→
发现新知
两个小正方形的面积之和等于大正方形的面积
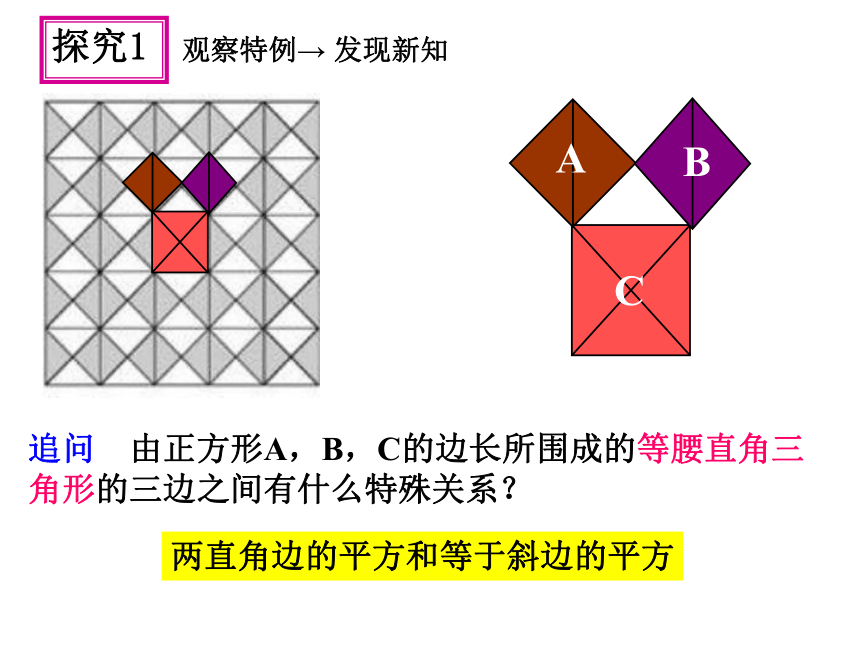
追问 由正方形A,B,C的边长所围成的等腰直角三角形的三边之间有什么特殊关系?
C
B
A
探究1
观察特例→
发现新知
两直角边的平方和等于斜边的平方
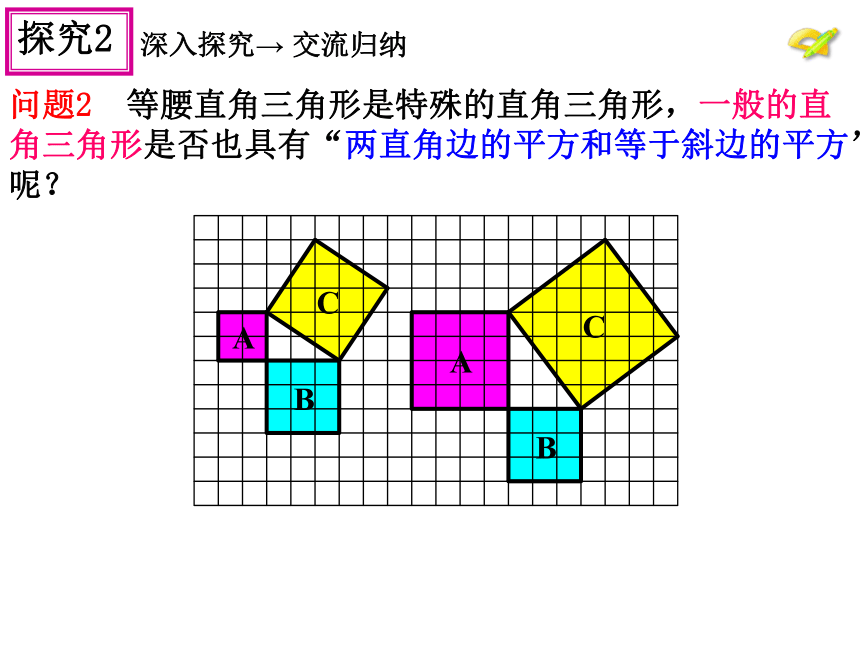
问题2 等腰直角三角形是特殊的直角三角形,一般的直角三角形是否也具有“两直角边的平方和等于斜边的平方”呢?
探究2
深入探究→
交流归纳
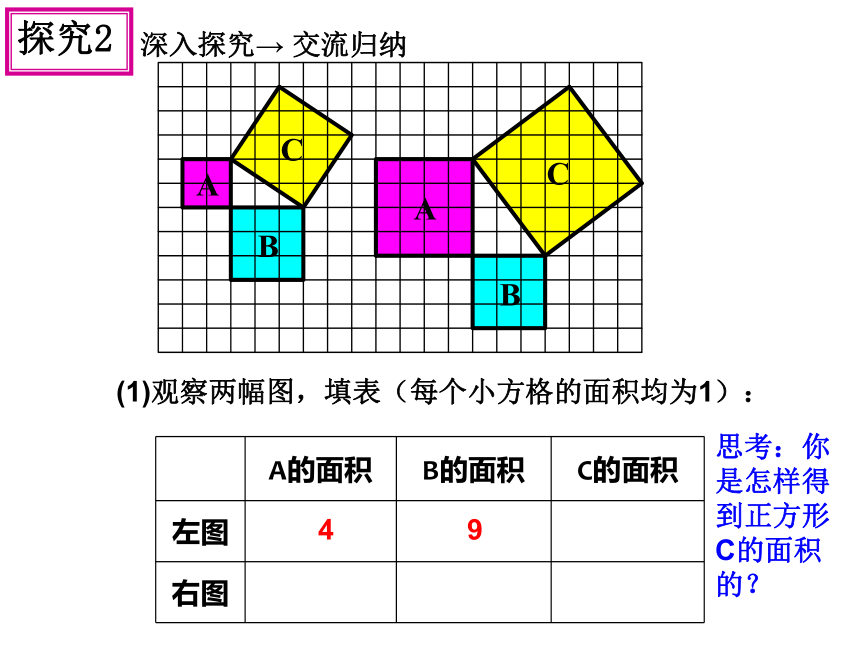
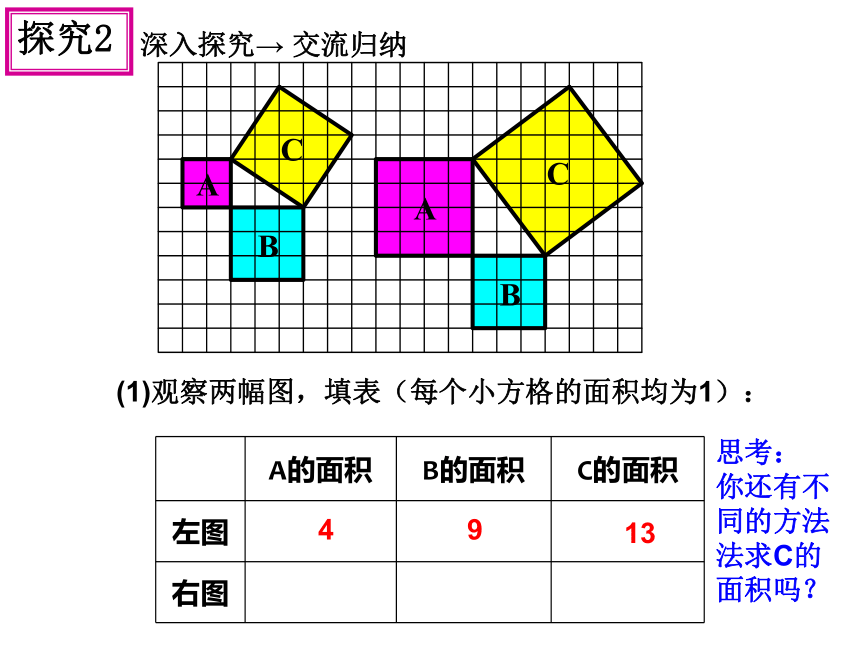
(1)观察两幅图,填表(每个小方格的面积均为1):
A的面积
B的面积
C的面积
左图
右图
4
探究2
深入探究→
交流归纳
9
思考:你是怎样得到正方形C的面积的?
探究2
深入探究→
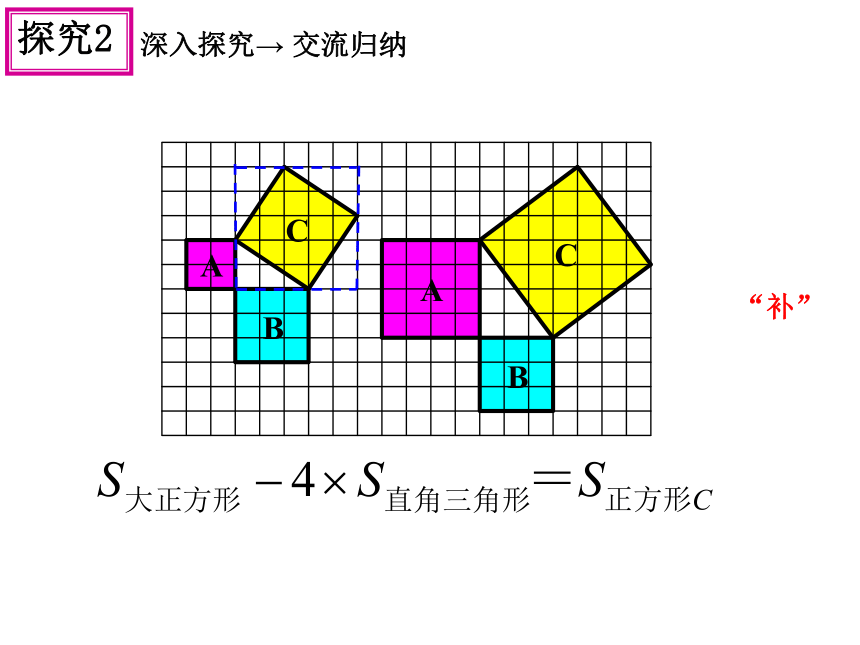
交流归纳
“补”
A的面积
B的面积
C的面积
左图
右图
4
探究2
深入探究→
交流归纳
9
13
思考:
你还有不同的方法法求C的
面积吗?
(1)观察两幅图,填表(每个小方格的面积均为1):
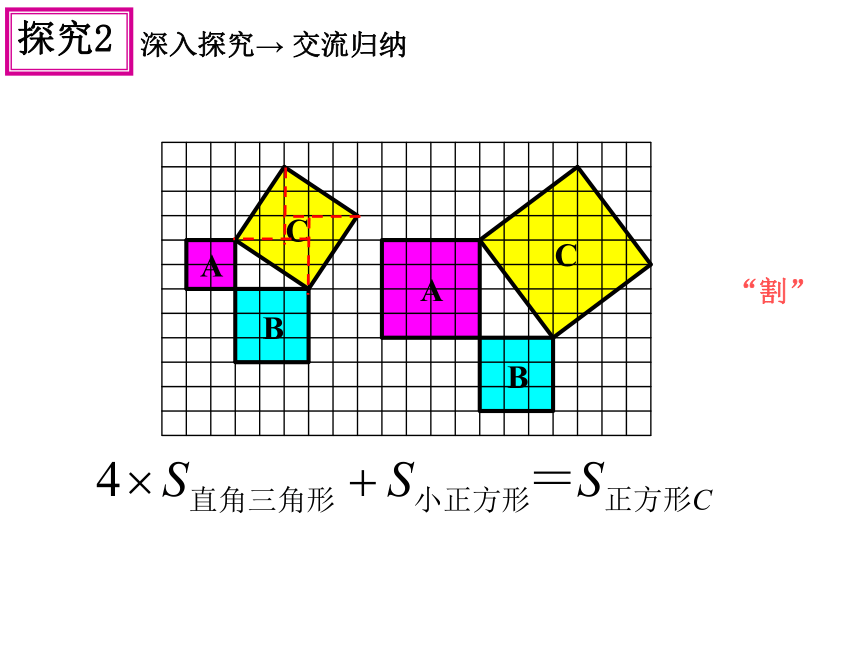
探究2
深入探究→
交流归纳
“割”
A的面积
B的面积
C的面积
左图
右图
4
9
探究2
深入探究→
交流归纳
13
(1)观察两幅图,填表(每个小方格的面积均为1):
A的面积
B的面积
C的面积
左图
右图
4
9
16
探究2
深入探究→
交流归纳
13
9
25
选择你喜欢
的方法求C
的面积
(1)观察两幅图,填表(每个小方格的面积均为1):
(2)分析填表数据,正方形A、B、C面积之间的关系是什么?
A的面积
B的面积
C的面积
左图
4
9
13
右图
16
9
25
探究2
深入探究→
交流归纳
追问 正方形A、B、C
所围成的直角三角形三边之间有怎样的特殊关系?
两直角边的平方和等于斜边的平方
如果直角三角形的两条直角边长分别为a、b,斜边长为c,那么
探究3
深入探究→
得出猜想
猜想:命题
问题3 一般情况下,如果任意直角三角形的两直角边分别为a,b,斜边长为c,猜想两直角边a,b与斜边c的关系?
c
a
b
c
a
b
1、准备四个全等的直角三角形(设直角三角形的两条直角边分别为a,b,斜边c);
2、你能用这四个直角三角形拼成一个正方形吗?
3、你拼的正方形中是否含有以斜边c为边的正方形?
4、你能否就你拼出的图说明a2+b2=c2?
割弦图
补
探究3
拼图验证→
加深理解
拼一拼
c
a
b
c
a
b
c
a
b
c
a
b
拼图1
割弦图
补
探究3
拼图验证→
加深理解
c2
(a+b)2
大正方形的面积可以表示为
;
小正方形的面积可以表示为
小正方形的面积也可以表示为:
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为
;
大正方形的面积也可以表示为
c2
4?
+(b-
a)2
∵
c2=
4?
+(b-a)2
拼图2
c
a
b
c
b
a
c
a
b
c
a
b
割弦图
补
探究3
拼图验证→
加深理解
a
b
c
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2
+
b2
=
c2
勾股定理
即
直角三角形两直角边的平方和等于斜边的平方。
经过证明被确认正确的命题叫做定理
勾
股
勾
弦
股
例.求出下列直角三角形中未知边的长度
初步应用定理
x
6
8
A
B
C
(1)
初步应用定理
练一练
1.在△ABC中,∠C=90°,a=3,b=4,则c=_____
2.在△ABC中,a=3,b=4,试求第三边c的值
3.在一个直角三角形中,两边长分别为3、4,
则第三边的长为_____
5
15
(1)必须是直角三角形
(2)弄清已知边是什么边
(3)弄清未知边是什么边
或
课堂小结
(1)勾股定理的内容是什么?它有什么作用?
(2)在探究勾股定理的过程中,我们经历了怎样
的探究过程?
(3)运用勾股定理应注意些什么?
求直角三角形中边的长度
网格中的直角三角形
等腰直角三角形
一般直角三角形
(1)必须是直角三角形
(2)弄清已知边是什么边
(3)弄清未知边是什么边
1.
请你利用今天学习的面积法证明教材习题17.3第13题.
2.
课下每个同学制作一张勾股定理的数学小报,并自己上网查阅与勾股定理有关的知识,证明方法和应用等,然后小组交流、展示.
作业布置
第十七章
冀教版初中数学八年级上册
17.3
勾股定理
毕达哥拉斯
(公元前572-前492年)
古希腊著名的哲学家
数学家。
情境引入
问题1 图中三个彩色正方形的面积有什么关系?
探究1
观察特例→
发现新知
两个小正方形的面积之和等于大正方形的面积
追问 由正方形A,B,C的边长所围成的等腰直角三角形的三边之间有什么特殊关系?
C
B
A
探究1
观察特例→
发现新知
两直角边的平方和等于斜边的平方
问题2 等腰直角三角形是特殊的直角三角形,一般的直角三角形是否也具有“两直角边的平方和等于斜边的平方”呢?
探究2
深入探究→
交流归纳
(1)观察两幅图,填表(每个小方格的面积均为1):
A的面积
B的面积
C的面积
左图
右图
4
探究2
深入探究→
交流归纳
9
思考:你是怎样得到正方形C的面积的?
探究2
深入探究→
交流归纳
“补”
A的面积
B的面积
C的面积
左图
右图
4
探究2
深入探究→
交流归纳
9
13
思考:
你还有不同的方法法求C的
面积吗?
(1)观察两幅图,填表(每个小方格的面积均为1):
探究2
深入探究→
交流归纳
“割”
A的面积
B的面积
C的面积
左图
右图
4
9
探究2
深入探究→
交流归纳
13
(1)观察两幅图,填表(每个小方格的面积均为1):
A的面积
B的面积
C的面积
左图
右图
4
9
16
探究2
深入探究→
交流归纳
13
9
25
选择你喜欢
的方法求C
的面积
(1)观察两幅图,填表(每个小方格的面积均为1):
(2)分析填表数据,正方形A、B、C面积之间的关系是什么?
A的面积
B的面积
C的面积
左图
4
9
13
右图
16
9
25
探究2
深入探究→
交流归纳
追问 正方形A、B、C
所围成的直角三角形三边之间有怎样的特殊关系?
两直角边的平方和等于斜边的平方
如果直角三角形的两条直角边长分别为a、b,斜边长为c,那么
探究3
深入探究→
得出猜想
猜想:命题
问题3 一般情况下,如果任意直角三角形的两直角边分别为a,b,斜边长为c,猜想两直角边a,b与斜边c的关系?
c
a
b
c
a
b
1、准备四个全等的直角三角形(设直角三角形的两条直角边分别为a,b,斜边c);
2、你能用这四个直角三角形拼成一个正方形吗?
3、你拼的正方形中是否含有以斜边c为边的正方形?
4、你能否就你拼出的图说明a2+b2=c2?
割弦图
补
探究3
拼图验证→
加深理解
拼一拼
c
a
b
c
a
b
c
a
b
c
a
b
拼图1
割弦图
补
探究3
拼图验证→
加深理解
c2
(a+b)2
大正方形的面积可以表示为
;
小正方形的面积可以表示为
小正方形的面积也可以表示为:
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为
;
大正方形的面积也可以表示为
c2
4?
+(b-
a)2
∵
c2=
4?
+(b-a)2
拼图2
c
a
b
c
b
a
c
a
b
c
a
b
割弦图
补
探究3
拼图验证→
加深理解
a
b
c
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2
+
b2
=
c2
勾股定理
即
直角三角形两直角边的平方和等于斜边的平方。
经过证明被确认正确的命题叫做定理
勾
股
勾
弦
股
例.求出下列直角三角形中未知边的长度
初步应用定理
x
6
8
A
B
C
(1)
初步应用定理
练一练
1.在△ABC中,∠C=90°,a=3,b=4,则c=_____
2.在△ABC中,a=3,b=4,试求第三边c的值
3.在一个直角三角形中,两边长分别为3、4,
则第三边的长为_____
5
1
(1)必须是直角三角形
(2)弄清已知边是什么边
(3)弄清未知边是什么边
或
课堂小结
(1)勾股定理的内容是什么?它有什么作用?
(2)在探究勾股定理的过程中,我们经历了怎样
的探究过程?
(3)运用勾股定理应注意些什么?
求直角三角形中边的长度
网格中的直角三角形
等腰直角三角形
一般直角三角形
(1)必须是直角三角形
(2)弄清已知边是什么边
(3)弄清未知边是什么边
1.
请你利用今天学习的面积法证明教材习题17.3第13题.
2.
课下每个同学制作一张勾股定理的数学小报,并自己上网查阅与勾股定理有关的知识,证明方法和应用等,然后小组交流、展示.
作业布置
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
