2021-2022冀教版数学八年级上册17.3勾股定理 课件(共24张PPT)
文档属性
| 名称 | 2021-2022冀教版数学八年级上册17.3勾股定理 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
17.3勾股定理
这个图案就是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”
2002年在北京召开了第24届国际数学家大会,它是最高水平的全球性数学科学学术会议,被誉为数学界的“奥运会”,这就是本届大会会徽的图案。
勾股定理的认识及验证
我们一起穿越回到2500年前,跟随毕达哥拉斯再去他那位老朋友家做客,看到他朋友家用等腰直角三角形砖铺成的地面(如图):
A
B
C
试问:正方形A、B、C面积之间有什么样的数量关系?
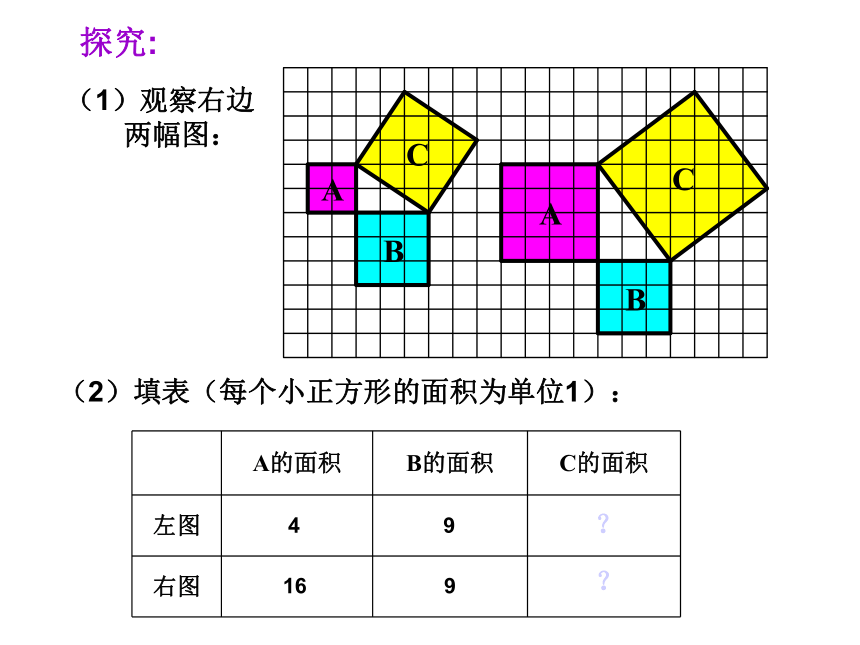
探究:
(1)观察右边
两幅图:
(2)填表(每个小正方形的面积为单位1):
A的面积
B的面积
C的面积
左图
右图
4
9
16
9
?
?
结论
以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
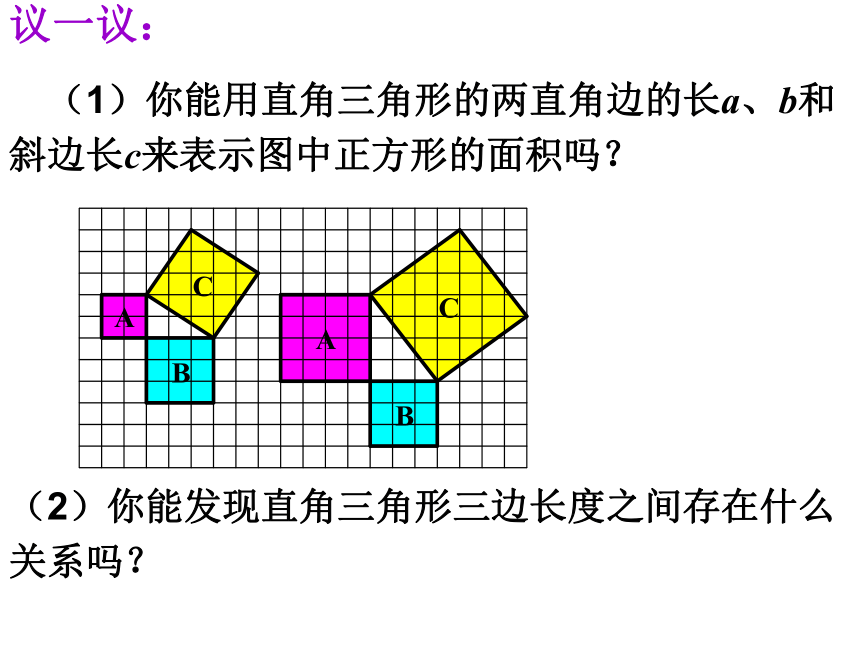
议一议:
(1)你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么
关系吗?
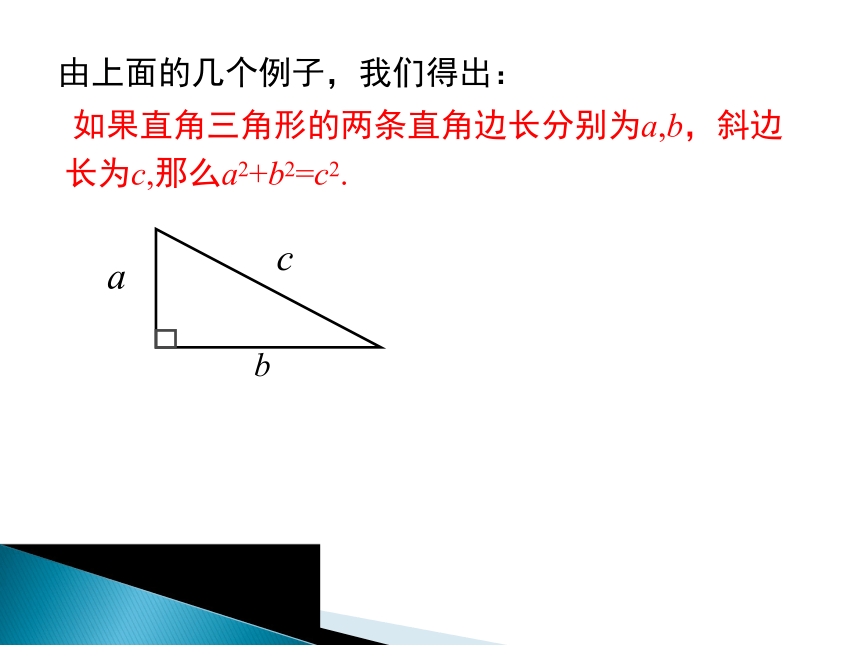
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
由上面的几个例子,我们得出:
a
b
c
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
勾2+股2=弦2
小贴士
下面动图形象的说明命题1的正确性,让我们跟着以前的数学家们用拼图法来证明这一猜想.
a
b
b
c
a
b
c
a
证法1
让我们跟着我国汉代数学家赵爽拼图,再用所拼的图形证明命题吧.
a
b
c
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
赵爽弦图
b-a
证明:
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.因为,这个图案被选为2002年在北京召开的国际数学大会的会徽.
证法2
毕达哥拉斯证法,请先用手中的四个全等的直角三角形按图示进行拼图,然后分析其面积关系后证明吧.
a
a
a
a
b
b
b
b
c
c
c
c
∴a2+b2+2ab=c2+2ab,
∴a2
+b2
=c2.
证明:
∵S大正方形=(a+b)2=a2+b2+2ab,
S大正方形=4S直角三角形+
S小正方形
=4×
ab+c2
=c2+2ab,
a
a
b
b
c
c
证法3
美国第二十任总统伽菲尔德的“总统证法”.(1876年)
如图,图中的三个三角形都是直角三角形,求证:a2
+
b2
=
c2.
我国数学家刘徽在他的《九章算术注》中给出的“青朱出入图”
:
a
b
c
青入
青方
青
出
青出
青入
朱入
朱方
朱出
青朱出入图
课外链接
如图,过
A
点画一直线
AL
使其垂直于
DE,
并交
DE
于
L,交
BC
于
M.通过证明△BCF≌△BDA,利用三角形面积与长方形面积的关系,得到正方形ABFG与矩形BDLM等积,同理正方形ACKH与
矩形MLEC也等积,于是推得
欧几里得证明勾股定理
推荐书目
练一练
求下列图中未知数x、y的值:
解:由勾股定理可得
81+
144=x2,
解得x=15.
解:由勾股定理可得
y2+
144=169,
解得
y=5
【变式题】
在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图?,
当BC为斜边时,如图?,
4
3
A
C
B
4
3
C
A
B
图?
图?
当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下一定要进行分类讨论,否则容易丢解.
归纳
A.8
米
B.9
米
C.10米
D.14米
1、如图,一个长8
米,宽6
米的草地,需在相对角的顶点间加一条小路,则小路的长为
(
)
8m
6m
别踩我,我怕疼!
2、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为
(
)
A
B
C
A.50米
B.120米
C.100米
D.130米
130
120
?
某楼房在20米高处的楼层失火,消防员取来25米长的云梯救火,已知梯子的底部离墙的距离是15米。问消防队员能否进入该楼层灭火?
已知两直角边求斜边
A
B
C
15
20
?
?
?
?
课堂小结
勾股定理
内容
在Rt△ABC中,
∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
注意
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
17.3勾股定理
这个图案就是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”
2002年在北京召开了第24届国际数学家大会,它是最高水平的全球性数学科学学术会议,被誉为数学界的“奥运会”,这就是本届大会会徽的图案。
勾股定理的认识及验证
我们一起穿越回到2500年前,跟随毕达哥拉斯再去他那位老朋友家做客,看到他朋友家用等腰直角三角形砖铺成的地面(如图):
A
B
C
试问:正方形A、B、C面积之间有什么样的数量关系?
探究:
(1)观察右边
两幅图:
(2)填表(每个小正方形的面积为单位1):
A的面积
B的面积
C的面积
左图
右图
4
9
16
9
?
?
结论
以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
议一议:
(1)你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么
关系吗?
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
由上面的几个例子,我们得出:
a
b
c
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
勾2+股2=弦2
小贴士
下面动图形象的说明命题1的正确性,让我们跟着以前的数学家们用拼图法来证明这一猜想.
a
b
b
c
a
b
c
a
证法1
让我们跟着我国汉代数学家赵爽拼图,再用所拼的图形证明命题吧.
a
b
c
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
赵爽弦图
b-a
证明:
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.因为,这个图案被选为2002年在北京召开的国际数学大会的会徽.
证法2
毕达哥拉斯证法,请先用手中的四个全等的直角三角形按图示进行拼图,然后分析其面积关系后证明吧.
a
a
a
a
b
b
b
b
c
c
c
c
∴a2+b2+2ab=c2+2ab,
∴a2
+b2
=c2.
证明:
∵S大正方形=(a+b)2=a2+b2+2ab,
S大正方形=4S直角三角形+
S小正方形
=4×
ab+c2
=c2+2ab,
a
a
b
b
c
c
证法3
美国第二十任总统伽菲尔德的“总统证法”.(1876年)
如图,图中的三个三角形都是直角三角形,求证:a2
+
b2
=
c2.
我国数学家刘徽在他的《九章算术注》中给出的“青朱出入图”
:
a
b
c
青入
青方
青
出
青出
青入
朱入
朱方
朱出
青朱出入图
课外链接
如图,过
A
点画一直线
AL
使其垂直于
DE,
并交
DE
于
L,交
BC
于
M.通过证明△BCF≌△BDA,利用三角形面积与长方形面积的关系,得到正方形ABFG与矩形BDLM等积,同理正方形ACKH与
矩形MLEC也等积,于是推得
欧几里得证明勾股定理
推荐书目
练一练
求下列图中未知数x、y的值:
解:由勾股定理可得
81+
144=x2,
解得x=15.
解:由勾股定理可得
y2+
144=169,
解得
y=5
【变式题】
在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图?,
当BC为斜边时,如图?,
4
3
A
C
B
4
3
C
A
B
图?
图?
当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下一定要进行分类讨论,否则容易丢解.
归纳
A.8
米
B.9
米
C.10米
D.14米
1、如图,一个长8
米,宽6
米的草地,需在相对角的顶点间加一条小路,则小路的长为
(
)
8m
6m
别踩我,我怕疼!
2、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为
(
)
A
B
C
A.50米
B.120米
C.100米
D.130米
130
120
?
某楼房在20米高处的楼层失火,消防员取来25米长的云梯救火,已知梯子的底部离墙的距离是15米。问消防队员能否进入该楼层灭火?
已知两直角边求斜边
A
B
C
15
20
?
?
?
?
课堂小结
勾股定理
内容
在Rt△ABC中,
∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
注意
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
