17.3勾股定理课件 冀教版数学八年级上册(22张)
文档属性
| 名称 | 17.3勾股定理课件 冀教版数学八年级上册(22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1022.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
§17.3
勾股定理
学习目标
1.经历
探索和验证勾股定理的过程,发展对图形性质或数量关系猜想及检验的能力,体会拼图验证的合理性。
2.能够利用勾股定理解决一些简单的实际问题
2002年世界数学家大会会标
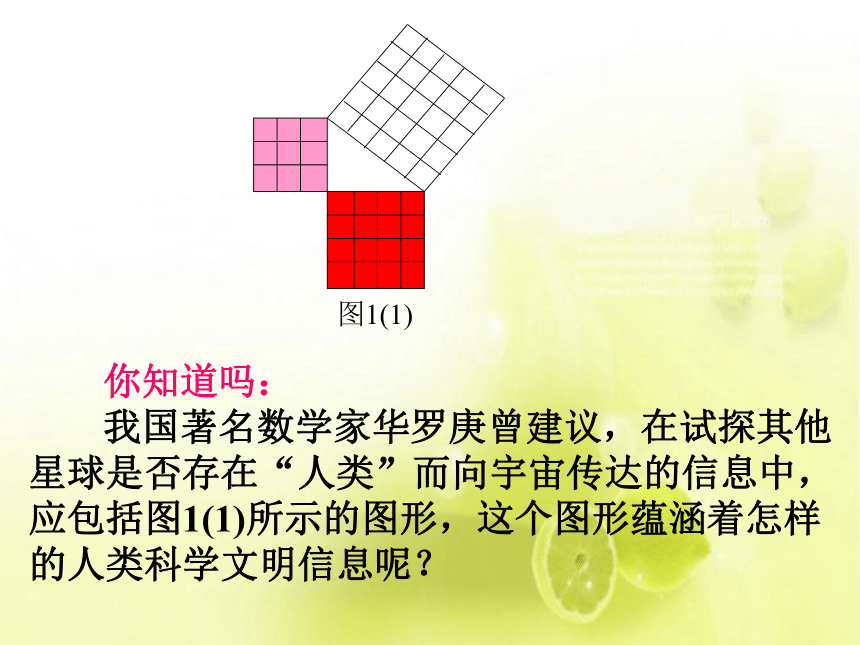
图1(1)
你知道吗:
我国著名数学家华罗庚曾建议,在试探其他星球是否存在“人类”而向宇宙传达的信息中,应包括图1(1)所示的图形,这个图形蕴涵着怎样的人类科学文明信息呢?
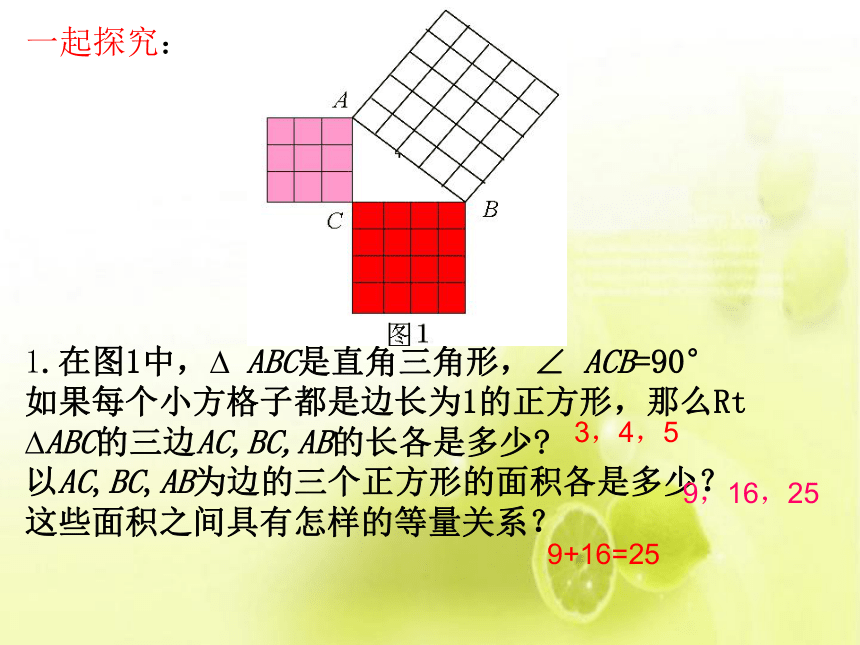
1.在图1中,?
ABC是直角三角形,∠
ACB=90°
如果每个小方格子都是边长为1的正方形,那么Rt
?ABC的三边AC,BC,AB的长各是多少?
以AC,BC,AB为边的三个正方形的面积各是多少?
这些面积之间具有怎样的等量关系?
一起探究:
3,4,5
9+16=25
9,16,25
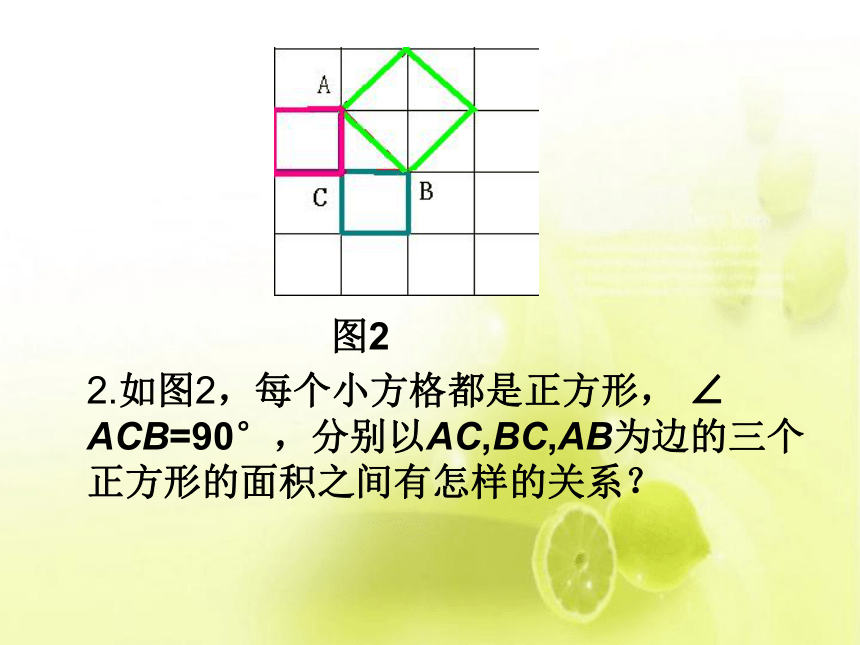
2.如图2,每个小方格都是正方形,
∠
ACB=90°,分别以AC,BC,AB为边的三个
正方形的面积之间有怎样的关系?
图2
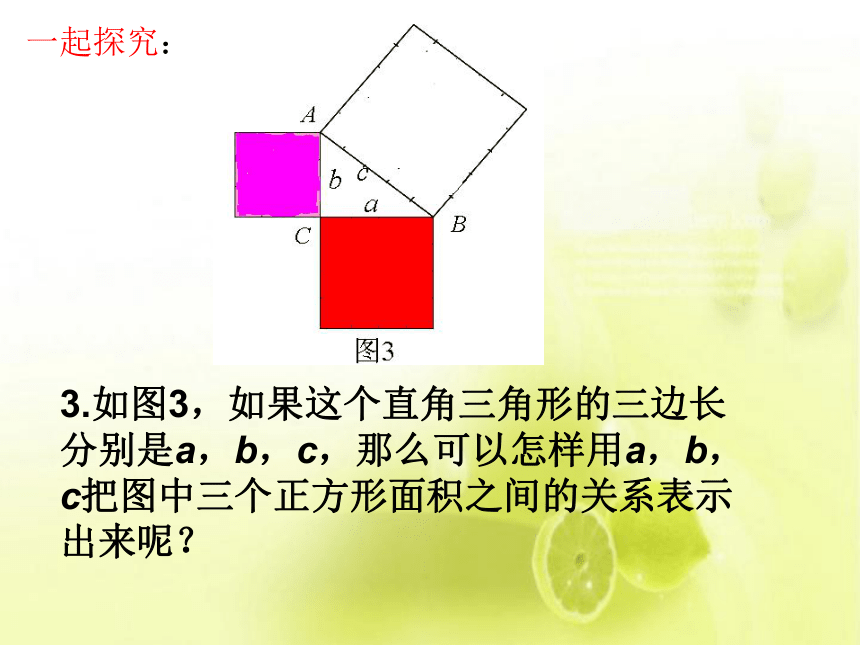
3.如图3,如果这个直角三角形的三边长分别是a,b,c,那么可以怎样用a,b,c把图中三个正方形面积之间的关系表示出来呢?
一起探究:
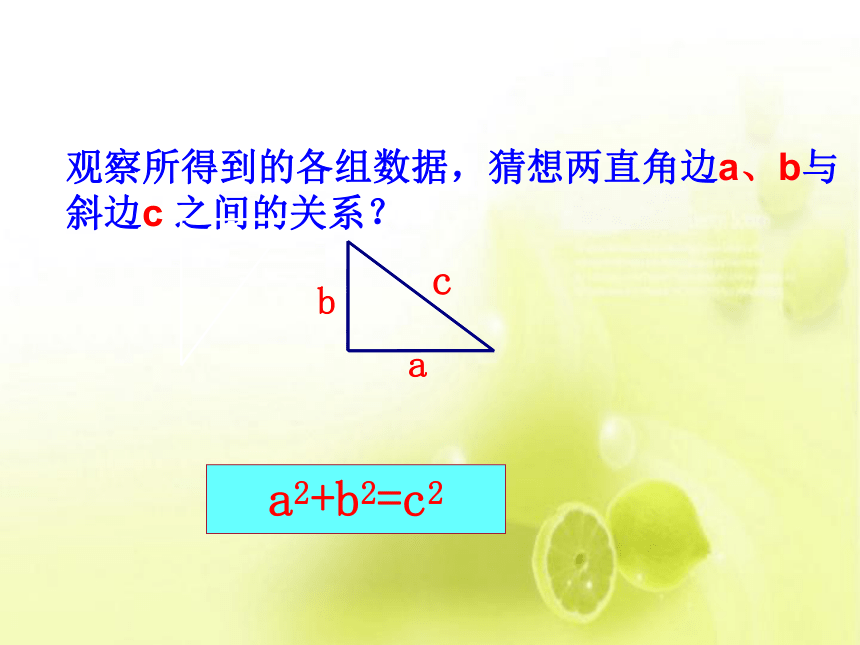
观察所得到的各组数据,猜想两直角边a、b与斜边c
之间的关系?
a2+b2=c2
a
c
b
┏
a2+b2=c2
a
c
b
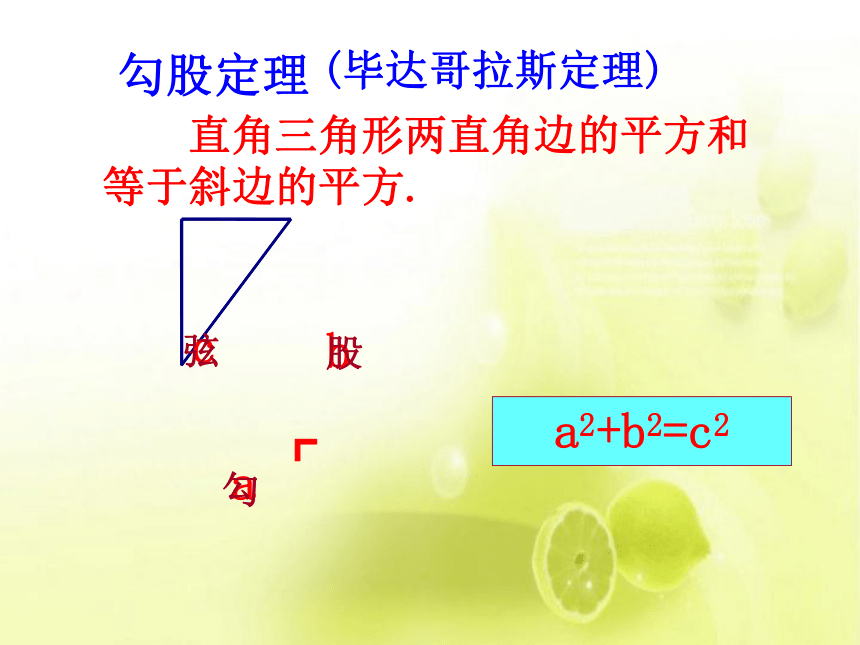
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
勾股定理
(毕达哥拉斯定理)
两千多年前,古希腊有个哥拉
斯学派,他们首先发现了勾股定理,因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派,1955
勾
股
世
界
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
a
b
c
a
b
c
b
a
c
a
b
c
用两种方法表示大正方形的面积:
a
b
c
b
c
b
c
b
c
a
a
a
试
一
试
我们用拼图的方法来说明勾股定理是正确的
“勾股圆方图”
c
b
?
a
c2
=
(b?
a)2
+
4(?ab)
=
b2
?
2ab
+
a2
+
2ab
b
a
?
a2
+
b2
=
c2
美国第二十任总统伽菲尔德的证法:
1、判断题:
1)若△ABC是直角三角形,直角边a=6,b=8,
则c=10.
2)
直角三角形的两边长分别是3和4,则另一边是5
3)直角三角形三边a,b,c一定满足下面的式子:
a?+b?
=c?
(√
)
(X
)
(X
)
实践与探索
2.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
X=15
y=5
Z=7
比一比看看谁算得快!
3.求下列直角三角形中未知边的长:
8
x
17
16
20
x
12
5
x
①X=15
②X=12
③X=13
1、如图,一个高3
米,宽4
米的大门,需在相对角的顶点间加一个加固木条,则木条的长为
(
)
A.3
米
B.4
米
C.5米
D.6米
C
3
4
2、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为
(
)
A
B
C
A.50米
B.120米
C.100米
D.130米
130
120
?
A
小实验:
如图,分别以直角三角形的三边为直径作三个半圆,这三个半圆的面积之间有什么关系?为什么?
课后作业
课本152页:习题1,2,3题.
§17.3
勾股定理
学习目标
1.经历
探索和验证勾股定理的过程,发展对图形性质或数量关系猜想及检验的能力,体会拼图验证的合理性。
2.能够利用勾股定理解决一些简单的实际问题
2002年世界数学家大会会标
图1(1)
你知道吗:
我国著名数学家华罗庚曾建议,在试探其他星球是否存在“人类”而向宇宙传达的信息中,应包括图1(1)所示的图形,这个图形蕴涵着怎样的人类科学文明信息呢?
1.在图1中,?
ABC是直角三角形,∠
ACB=90°
如果每个小方格子都是边长为1的正方形,那么Rt
?ABC的三边AC,BC,AB的长各是多少?
以AC,BC,AB为边的三个正方形的面积各是多少?
这些面积之间具有怎样的等量关系?
一起探究:
3,4,5
9+16=25
9,16,25
2.如图2,每个小方格都是正方形,
∠
ACB=90°,分别以AC,BC,AB为边的三个
正方形的面积之间有怎样的关系?
图2
3.如图3,如果这个直角三角形的三边长分别是a,b,c,那么可以怎样用a,b,c把图中三个正方形面积之间的关系表示出来呢?
一起探究:
观察所得到的各组数据,猜想两直角边a、b与斜边c
之间的关系?
a2+b2=c2
a
c
b
┏
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
勾股定理
(毕达哥拉斯定理)
两千多年前,古希腊有个哥拉
斯学派,他们首先发现了勾股定理,因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派,1955
勾
股
世
界
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
a
b
c
a
b
c
b
a
c
a
b
c
用两种方法表示大正方形的面积:
a
b
c
b
c
b
c
b
c
a
a
a
试
一
试
我们用拼图的方法来说明勾股定理是正确的
“勾股圆方图”
c
b
?
a
c2
=
(b?
a)2
+
4(?ab)
=
b2
?
2ab
+
a2
+
2ab
b
a
?
a2
+
b2
=
c2
美国第二十任总统伽菲尔德的证法:
1、判断题:
1)若△ABC是直角三角形,直角边a=6,b=8,
则c=10.
2)
直角三角形的两边长分别是3和4,则另一边是5
3)直角三角形三边a,b,c一定满足下面的式子:
a?+b?
=c?
(√
)
(X
)
(X
)
实践与探索
2.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
X=15
y=5
Z=7
比一比看看谁算得快!
3.求下列直角三角形中未知边的长:
8
x
17
16
20
x
12
5
x
①X=15
②X=12
③X=13
1、如图,一个高3
米,宽4
米的大门,需在相对角的顶点间加一个加固木条,则木条的长为
(
)
A.3
米
B.4
米
C.5米
D.6米
C
3
4
2、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为
(
)
A
B
C
A.50米
B.120米
C.100米
D.130米
130
120
?
A
小实验:
如图,分别以直角三角形的三边为直径作三个半圆,这三个半圆的面积之间有什么关系?为什么?
课后作业
课本152页:习题1,2,3题.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
