17.4直角三角形全等的判定课件 冀教版数学八年级上册 (25张)
文档属性
| 名称 | 17.4直角三角形全等的判定课件 冀教版数学八年级上册 (25张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 12:13:09 | ||
图片预览








文档简介
(共25张PPT)
1.经历两个直角三角形全等条件的探究过程,掌握直角三角形全等的条件;
2.会利用两个直角三角形全等的条件解决简单的实际问题。
学习目标
重点:掌握判定两直角三角形全等的条件;运用直角三角形全等的条件解决实际问题。
难点:探索“HL”定理,灵活运用直角三角形全等的条件来解决实际问题。
学习重点和难点
1.三角形全等的判定方法
(1)三边
(2)两边及其夹角
(3)两角及其夹边
(4)两角及一角对边
(SSS)
(SAS)
(ASA)
(AAS)
知
识
链
接
如果直角三角形两直角边分别为a、b,斜边为c,那么
3.尺规作图:做一个角等于90。
预习交流
2.勾股定理:
元旦将至,子硕师友组承办了舞台设计:背景的形状是两个直角三角形,为了美观,他们想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量。
问题1:
情境导入
问题1:
B
D
F
C
E
A
子硕师友准备了刻度尺和量角器,能完成这项任务吗?
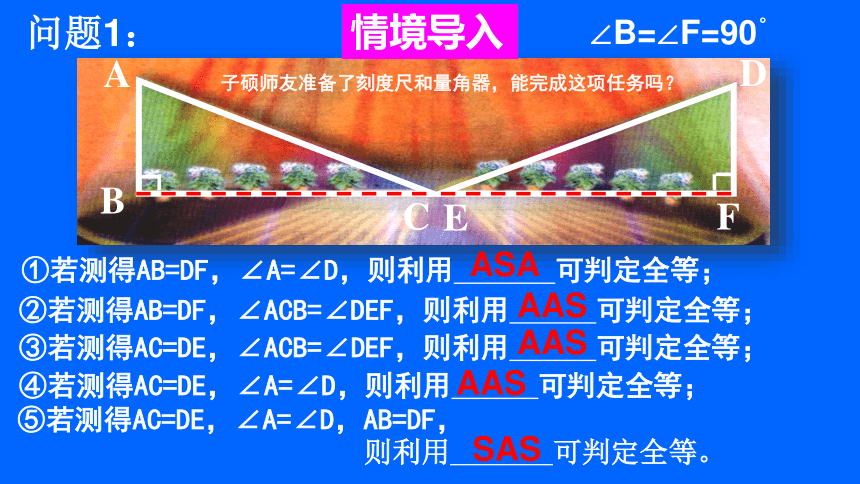
∠B=∠F=90。
①若测得AB=DF,∠A=∠D,则利用
可判定全等;
ASA
②若测得AB=DF,∠ACB=∠DEF,则利用
可判定全等;
AAS
③若测得AC=DE,∠ACB=∠DEF,则利用
可判定全等;
AAS
④若测得AC=DE,∠A=∠D,则利用
可判定全等;
AAS
⑤若测得AC=DE,∠A=∠D,AB=DF,
则利用
可判定全等。
SAS
情境导入
问题2:
B
D
F
C
E
A
如果子硕师友只带了刻度尺,能完成这项任务吗?
情境导入
子硕师友是这样做的,他测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”。你相信他的结论吗?
A
B
D
F
C
E
问题2:
情境导入
A
B
D
F
C
E
问题2:
情境导入
对于两个直角三角形,若满足一条直角边和一条斜边对应相等时,这两个直角三角形全等吗?
已知:如图,∠C=
90°,利用它做一个直角三角形,使该直角三角形的一条直角边BC=5cm,斜边AB=13cm。
动手操作
∟
B
C
C
A
B
互助探究
直角三角形全等的判定
思考:如果我们手中的直角三角形的一直角边和斜边长分别为a、c,那么它们还全等吗?
猜想:斜边和直角边对应相等的两个直角三角形
。
互助探究
直角三角形全等的判定
全等
A
B
C
A′
B′
C′
已知:如图,在△ABC和
△A'
B'C'
,∠ACB=∠A'C'B'=90°
AC=A'C',AB=A'B'
求证:
△ABC≌△A'B'C'
直角三角形全等的判定定理
互助探究
∟
∟
直角三角形全等的判定定理
证明:在△ABC和△A'B'C'中,
∵∠ACB=90°∠A'C'B'=90°
∵
AB=A'
B'
,AC=A'
C'
,
∴
BC=B'
C'
.
在△ABC和△
A'B'C'中
AB=A'B'
∵
BC=B'C'
AC=A'C'
∴△ABC≌△A'B'C'
(SSS).
互助探究
∴
BC2=AB2-AC2(勾股定理).
B'
C'
2=A'B'2-A'C'2
(勾股定理)
A
B
C
∟
A′
B′
C′
∟
斜边和一条直角边对应相等的两个直角三角形全等,
数学语言:
AB=A?B?
在Rt△ABC和Rt△A?B?C?中
Rt△ABC≌
Rt△A?B?C?
∴
∟
B
?
C?
A
?
∟
B
C
A
(HL)
BC=B?C?
∵
简写为“斜边、直角边”或“HL”。
直角三角形全等的判定定理
互助探究
1、下列判断对吗?并说明理由:
(1)一边及一个锐角对应相等的两个直角三角形
全等.(
)
(2)两直角边对应相等的两个直角三角形全等.(
)
(3)有两条边分别相等的两个直角三角形全等.(
)
√
√
X
跟踪训练
2、
如图,
∠ACB
=∠ADB=90。,要证明△ABC≌
△BAD,还需一个什么条件?把这些条件都写出来,并在相应的括号内填写出判定它们全等的理由。
(1)
(
)
(2)
(
)
(3)
(
)
(4)
(
)
A
B
D
C
跟踪训练
已知:如图,点P在∠AOB的内部,PC⊥OA,PD⊥OB,垂足分别为C,D,
PC=PD
求证: 点P在∠AOB的平分线上.
A
O
B
D
C
P
证明:作射线OP,
∵
PC⊥OA,PD⊥OB,
∴
∠PCO=∠PDO=90°
,
在RtΔOPC和RtΔOPD中,
{
PC=PD
(已知)
OP=OP(公共边)
∵
∴
RtΔOPC≌RtΔOPD(HL)
∴
∠POA=∠POB
∴
OP是∠AOB的平分线,即点P在∠AOB的平分线上.
例题解析
已知:如图,在△ABC中,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别为E、F,且DE=DF
求证:△ABC是等腰三角形。
D
跟踪训练
互助提高
1、已知:如图,CE⊥AB,DF⊥AB,垂足分别为E,F,AF=BE,且AC=BD,则不正确的结论是(
)
A.Rt△AEC≌Rt△BFD
B.∠C+∠B=90°
C.∠A=∠D
D.AC∥BD
C
A
E
C
B
F
D
2、在△ABC
中,AB=AC,DE是过点A的直线,
BD⊥DE
于D,CE⊥DE
于E.
(1)若BC在DE的同侧(如图①)且AD=CE,
说明:BA⊥AC.
互助提高
①
2、在△ABC
中,AB=AC,DE是过点A的直线,
BD⊥DE
于D,CE⊥DE于E.
(2)若BC在DE的两侧(如图②),且AD=CE,
问AB与AC仍垂直吗?
互助提高
A
B
C
D
E
②
1、斜边、直角边(HL)定理:斜边和一条直角边对应相等的两个直角三角形全等。
2、证明两个直角三角形全等,不仅可以
用HL定理,还可以用SAS、ASA、SSS、AAS定理来证明两个三角形全等。
归纳总结
直角三角形全等的判定
直角三角形
角的关系
边之间的关系
边和其他线段
的关系
勾股定理
直角三角形
两锐角互余
HL
斜边上的中线等于
斜边的一半
300角所对直角边
等于斜边的一半
SAS、ASA、
SSS、AAS
直角三角形的判定
勾股定理逆定理
两个角互余
构建知识树
分层作业
课本P161全体同学做A组第2题
A、B同学做B组第一题
C、D同学做A组第一题
作业布置
1.经历两个直角三角形全等条件的探究过程,掌握直角三角形全等的条件;
2.会利用两个直角三角形全等的条件解决简单的实际问题。
学习目标
重点:掌握判定两直角三角形全等的条件;运用直角三角形全等的条件解决实际问题。
难点:探索“HL”定理,灵活运用直角三角形全等的条件来解决实际问题。
学习重点和难点
1.三角形全等的判定方法
(1)三边
(2)两边及其夹角
(3)两角及其夹边
(4)两角及一角对边
(SSS)
(SAS)
(ASA)
(AAS)
知
识
链
接
如果直角三角形两直角边分别为a、b,斜边为c,那么
3.尺规作图:做一个角等于90。
预习交流
2.勾股定理:
元旦将至,子硕师友组承办了舞台设计:背景的形状是两个直角三角形,为了美观,他们想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量。
问题1:
情境导入
问题1:
B
D
F
C
E
A
子硕师友准备了刻度尺和量角器,能完成这项任务吗?
∠B=∠F=90。
①若测得AB=DF,∠A=∠D,则利用
可判定全等;
ASA
②若测得AB=DF,∠ACB=∠DEF,则利用
可判定全等;
AAS
③若测得AC=DE,∠ACB=∠DEF,则利用
可判定全等;
AAS
④若测得AC=DE,∠A=∠D,则利用
可判定全等;
AAS
⑤若测得AC=DE,∠A=∠D,AB=DF,
则利用
可判定全等。
SAS
情境导入
问题2:
B
D
F
C
E
A
如果子硕师友只带了刻度尺,能完成这项任务吗?
情境导入
子硕师友是这样做的,他测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”。你相信他的结论吗?
A
B
D
F
C
E
问题2:
情境导入
A
B
D
F
C
E
问题2:
情境导入
对于两个直角三角形,若满足一条直角边和一条斜边对应相等时,这两个直角三角形全等吗?
已知:如图,∠C=
90°,利用它做一个直角三角形,使该直角三角形的一条直角边BC=5cm,斜边AB=13cm。
动手操作
∟
B
C
C
A
B
互助探究
直角三角形全等的判定
思考:如果我们手中的直角三角形的一直角边和斜边长分别为a、c,那么它们还全等吗?
猜想:斜边和直角边对应相等的两个直角三角形
。
互助探究
直角三角形全等的判定
全等
A
B
C
A′
B′
C′
已知:如图,在△ABC和
△A'
B'C'
,∠ACB=∠A'C'B'=90°
AC=A'C',AB=A'B'
求证:
△ABC≌△A'B'C'
直角三角形全等的判定定理
互助探究
∟
∟
直角三角形全等的判定定理
证明:在△ABC和△A'B'C'中,
∵∠ACB=90°∠A'C'B'=90°
∵
AB=A'
B'
,AC=A'
C'
,
∴
BC=B'
C'
.
在△ABC和△
A'B'C'中
AB=A'B'
∵
BC=B'C'
AC=A'C'
∴△ABC≌△A'B'C'
(SSS).
互助探究
∴
BC2=AB2-AC2(勾股定理).
B'
C'
2=A'B'2-A'C'2
(勾股定理)
A
B
C
∟
A′
B′
C′
∟
斜边和一条直角边对应相等的两个直角三角形全等,
数学语言:
AB=A?B?
在Rt△ABC和Rt△A?B?C?中
Rt△ABC≌
Rt△A?B?C?
∴
∟
B
?
C?
A
?
∟
B
C
A
(HL)
BC=B?C?
∵
简写为“斜边、直角边”或“HL”。
直角三角形全等的判定定理
互助探究
1、下列判断对吗?并说明理由:
(1)一边及一个锐角对应相等的两个直角三角形
全等.(
)
(2)两直角边对应相等的两个直角三角形全等.(
)
(3)有两条边分别相等的两个直角三角形全等.(
)
√
√
X
跟踪训练
2、
如图,
∠ACB
=∠ADB=90。,要证明△ABC≌
△BAD,还需一个什么条件?把这些条件都写出来,并在相应的括号内填写出判定它们全等的理由。
(1)
(
)
(2)
(
)
(3)
(
)
(4)
(
)
A
B
D
C
跟踪训练
已知:如图,点P在∠AOB的内部,PC⊥OA,PD⊥OB,垂足分别为C,D,
PC=PD
求证: 点P在∠AOB的平分线上.
A
O
B
D
C
P
证明:作射线OP,
∵
PC⊥OA,PD⊥OB,
∴
∠PCO=∠PDO=90°
,
在RtΔOPC和RtΔOPD中,
{
PC=PD
(已知)
OP=OP(公共边)
∵
∴
RtΔOPC≌RtΔOPD(HL)
∴
∠POA=∠POB
∴
OP是∠AOB的平分线,即点P在∠AOB的平分线上.
例题解析
已知:如图,在△ABC中,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别为E、F,且DE=DF
求证:△ABC是等腰三角形。
D
跟踪训练
互助提高
1、已知:如图,CE⊥AB,DF⊥AB,垂足分别为E,F,AF=BE,且AC=BD,则不正确的结论是(
)
A.Rt△AEC≌Rt△BFD
B.∠C+∠B=90°
C.∠A=∠D
D.AC∥BD
C
A
E
C
B
F
D
2、在△ABC
中,AB=AC,DE是过点A的直线,
BD⊥DE
于D,CE⊥DE
于E.
(1)若BC在DE的同侧(如图①)且AD=CE,
说明:BA⊥AC.
互助提高
①
2、在△ABC
中,AB=AC,DE是过点A的直线,
BD⊥DE
于D,CE⊥DE于E.
(2)若BC在DE的两侧(如图②),且AD=CE,
问AB与AC仍垂直吗?
互助提高
A
B
C
D
E
②
1、斜边、直角边(HL)定理:斜边和一条直角边对应相等的两个直角三角形全等。
2、证明两个直角三角形全等,不仅可以
用HL定理,还可以用SAS、ASA、SSS、AAS定理来证明两个三角形全等。
归纳总结
直角三角形全等的判定
直角三角形
角的关系
边之间的关系
边和其他线段
的关系
勾股定理
直角三角形
两锐角互余
HL
斜边上的中线等于
斜边的一半
300角所对直角边
等于斜边的一半
SAS、ASA、
SSS、AAS
直角三角形的判定
勾股定理逆定理
两个角互余
构建知识树
分层作业
课本P161全体同学做A组第2题
A、B同学做B组第一题
C、D同学做A组第一题
作业布置
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
