冀教版数学八年级上册17.4直角三角形全等的判定课件 (25张ppt)
文档属性
| 名称 | 冀教版数学八年级上册17.4直角三角形全等的判定课件 (25张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 694.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 15:15:51 | ||
图片预览





文档简介
(共25张PPT)
17.4直角三角形全等的判定
复习提问
证明一般两个三角形全等有哪些方法?
1.在两个三角形中,如果有两个角及它们的夹边对应相等,那么这两个三角形全等(简记为A.S.A)
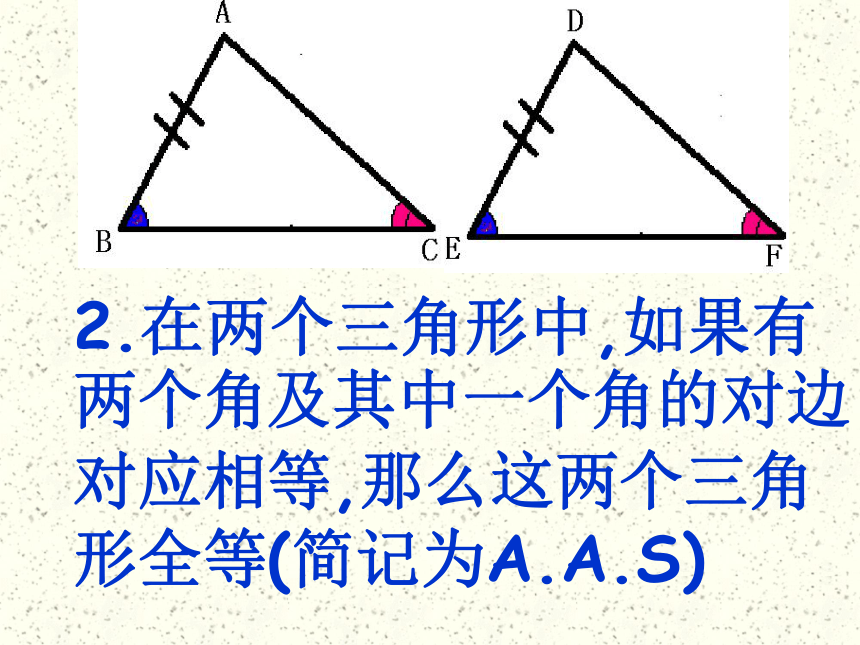
2.在两个三角形中,如果有两个角及其中一个角的对边对应相等,那么这两个三角形全等(简记为A.A.S)
3.在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等(简记为S.A.S)
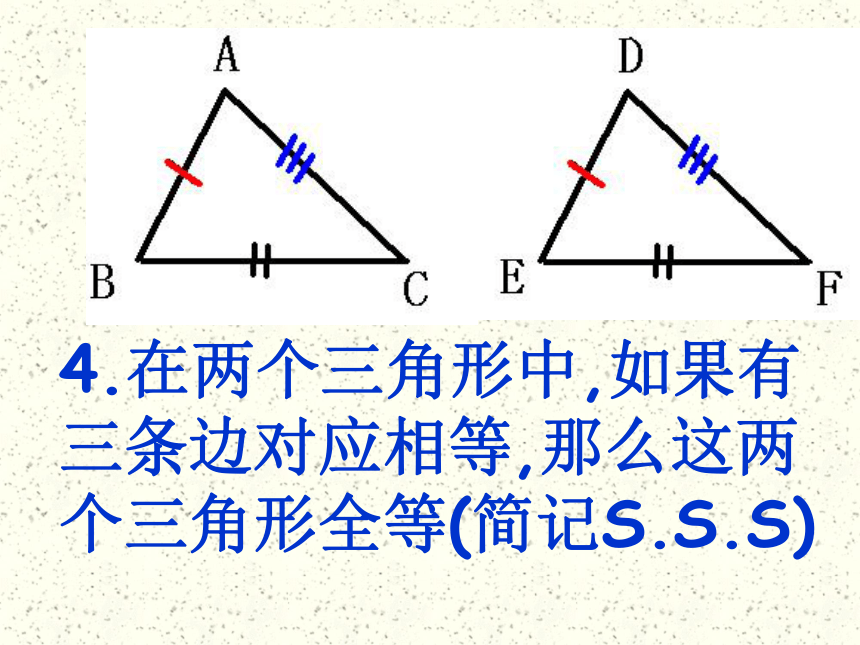
4.在两个三角形中,如果有三条边对应相等,那么这两个三角形全等(简记S.S.S)
判断:
满足下列条件的两个三角形是否全等?为什么?
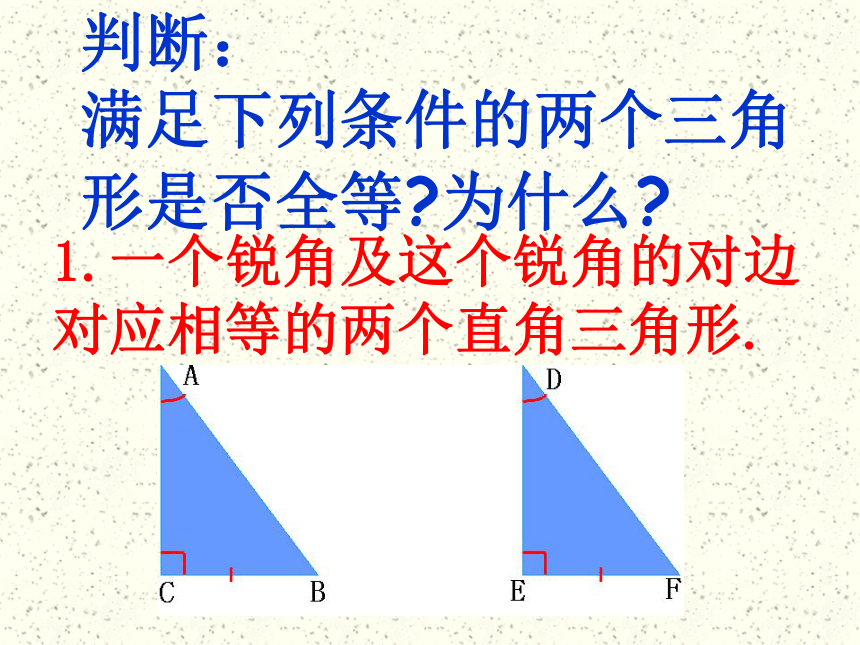
1.一个锐角及这个锐角的对边对应相等的两个直角三角形.
2.一个锐角及这个锐角相邻的直角边对应相等的两个直角三角形.
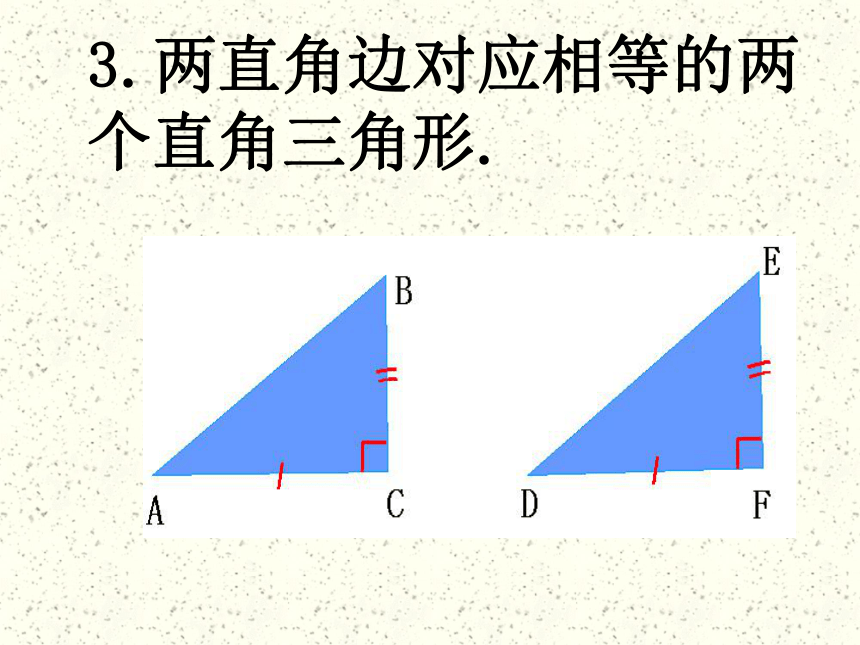
3.两直角边对应相等的两个直角三角形.
想一想
对于一般的三角形“S.S.A”可不可以证明三角形全等?
A
B
C
D
但直角三角形作为特殊的三角形,
会不会有自身独特的判定方法呢
?
动动手
做一做
画一个Rt△ABC,使得∠C=90°,一直角边CA=
8cm,斜边AB=10cm.
A
B
C
10cm
10cm
10cm
10cm
10cm
8cm
8cm
8cm
8cm
8cm
动动手
做一做
1:画∠MCN=90°;
C
N
M
动动手
做一做
1:画∠MCN=90°;
C
N
M
2:在射线CM上截取CA=8cm;
A
1:画∠MCN=90°;
2:在射线CM上截取CA=8cm;
动动手
做一做
3:以A为圆心,10cm为半径画弧,交射线CN于B;
C
N
M
A
B
C
N
M
B
动动手
做一做
A
4:连结AB;
△ABC即为所要
画的三角形
1:画∠MCN=90°;
2:在射线CM上截取CA=8cm;
3:以A为圆心,10cm为半径画弧,交射线CN于B;
把我们刚画好的直角三角形剪下来,和同桌的比比看,这些直角三角形有怎样的关系呢?
A
B
C
10cm
10cm
10cm
10cm
10cm
8cm
8cm
8cm
8cm
8cm
A′
B
′
C
′
10cm
10cm
10cm
10cm
10cm
8cm
8cm
8cm
8cm
8cm
Rt△ABC≌Rt△A′B′C′
斜边、直角边公理
有斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”
或“HL”
斜边、直角边公理
(HL)推理格式
A
B
C
A
′
B′
C
′
∴在Rt△ABC和Rt△
中
AB=
BC=
∴Rt△ABC≌
∵∠C=∠C′=90°
Rt△
(HL)
例1
已知:如图,在△ABC和△ABD中,AC⊥BC,
AD⊥BD,
垂足分别为C,D,AD=BC,求证:
△ABC≌△BAD.
A
B
D
C
例2已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF
A
B
C
P
E
F
Q
D
1.
如图∠C=
∠D=Rt
∠
,要证明△ACB≌
△BDA
,至少再补充几个条件,应补充什么条件?把它们分别写出来。
A
B
C
D
练习
2.如图
在△ABC中,已知BD⊥AC,CE
⊥AB,BD=CE。说明△EBC≌
△DCB的理由。
A
B
C
∟
∟
E
D
小结
直角三角形全等的判定
一般三角形全等的判定
“S.A.S”
“
A.S.A
”
“
A.A.S
”
“
S.S.S
”
“
S.A.S
”
“
A.S.A
”
“
A.A.S
”
“
H.L
”
灵活运用各种方法证明直角三角形全等
再见
17.4直角三角形全等的判定
复习提问
证明一般两个三角形全等有哪些方法?
1.在两个三角形中,如果有两个角及它们的夹边对应相等,那么这两个三角形全等(简记为A.S.A)
2.在两个三角形中,如果有两个角及其中一个角的对边对应相等,那么这两个三角形全等(简记为A.A.S)
3.在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等(简记为S.A.S)
4.在两个三角形中,如果有三条边对应相等,那么这两个三角形全等(简记S.S.S)
判断:
满足下列条件的两个三角形是否全等?为什么?
1.一个锐角及这个锐角的对边对应相等的两个直角三角形.
2.一个锐角及这个锐角相邻的直角边对应相等的两个直角三角形.
3.两直角边对应相等的两个直角三角形.
想一想
对于一般的三角形“S.S.A”可不可以证明三角形全等?
A
B
C
D
但直角三角形作为特殊的三角形,
会不会有自身独特的判定方法呢
?
动动手
做一做
画一个Rt△ABC,使得∠C=90°,一直角边CA=
8cm,斜边AB=10cm.
A
B
C
10cm
10cm
10cm
10cm
10cm
8cm
8cm
8cm
8cm
8cm
动动手
做一做
1:画∠MCN=90°;
C
N
M
动动手
做一做
1:画∠MCN=90°;
C
N
M
2:在射线CM上截取CA=8cm;
A
1:画∠MCN=90°;
2:在射线CM上截取CA=8cm;
动动手
做一做
3:以A为圆心,10cm为半径画弧,交射线CN于B;
C
N
M
A
B
C
N
M
B
动动手
做一做
A
4:连结AB;
△ABC即为所要
画的三角形
1:画∠MCN=90°;
2:在射线CM上截取CA=8cm;
3:以A为圆心,10cm为半径画弧,交射线CN于B;
把我们刚画好的直角三角形剪下来,和同桌的比比看,这些直角三角形有怎样的关系呢?
A
B
C
10cm
10cm
10cm
10cm
10cm
8cm
8cm
8cm
8cm
8cm
A′
B
′
C
′
10cm
10cm
10cm
10cm
10cm
8cm
8cm
8cm
8cm
8cm
Rt△ABC≌Rt△A′B′C′
斜边、直角边公理
有斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”
或“HL”
斜边、直角边公理
(HL)推理格式
A
B
C
A
′
B′
C
′
∴在Rt△ABC和Rt△
中
AB=
BC=
∴Rt△ABC≌
∵∠C=∠C′=90°
Rt△
(HL)
例1
已知:如图,在△ABC和△ABD中,AC⊥BC,
AD⊥BD,
垂足分别为C,D,AD=BC,求证:
△ABC≌△BAD.
A
B
D
C
例2已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF
A
B
C
P
E
F
Q
D
1.
如图∠C=
∠D=Rt
∠
,要证明△ACB≌
△BDA
,至少再补充几个条件,应补充什么条件?把它们分别写出来。
A
B
C
D
练习
2.如图
在△ABC中,已知BD⊥AC,CE
⊥AB,BD=CE。说明△EBC≌
△DCB的理由。
A
B
C
∟
∟
E
D
小结
直角三角形全等的判定
一般三角形全等的判定
“S.A.S”
“
A.S.A
”
“
A.A.S
”
“
S.S.S
”
“
S.A.S
”
“
A.S.A
”
“
A.A.S
”
“
H.L
”
灵活运用各种方法证明直角三角形全等
再见
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
