17.4直角三角形全等的判定课件 冀教版数学八年级上册(29张)
文档属性
| 名称 | 17.4直角三角形全等的判定课件 冀教版数学八年级上册(29张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 12:34:41 | ||
图片预览





文档简介
(共29张PPT)
17.4直角三角形全等的判定
三角形全等的判定方法有哪些?
复习巩固
SSS(三边对应相等的两个三角形全等)
ASA(两角和它们的夹边对应相等的两个三角形全等)
SAS(两边和它们的夹角对应相等的两个三角形全等)
AAS(两角和其中一角的对边对应相等的两个三角形全等)
复习巩固
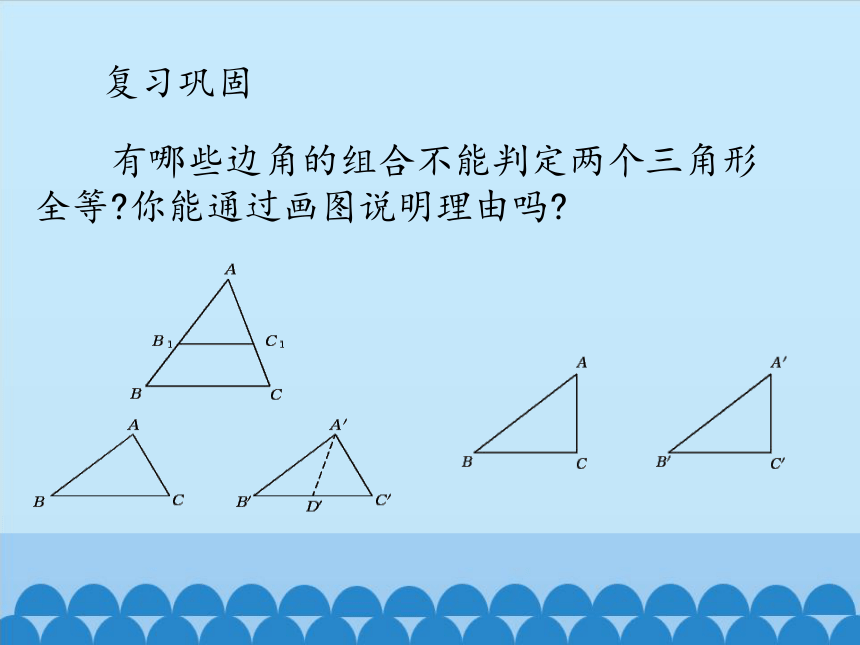
有哪些边角的组合不能判定两个三角形全等?你能通过画图说明理由吗?
如图(1)所示,已知两条线段(这两条线段长不相等),以长的线段为斜边、短的线段为一条直角边,画一个直角三角形.所有的直角三角形都全等吗?
学习新知
1.画一线段AB,使它等于4cm;
2.画∠EAB=90°;
3.以点B为圆心,以5cm长为半径画弧,交射线AE于点C;
4.连接BC,△ABC即为所求,
如图(2)所示.
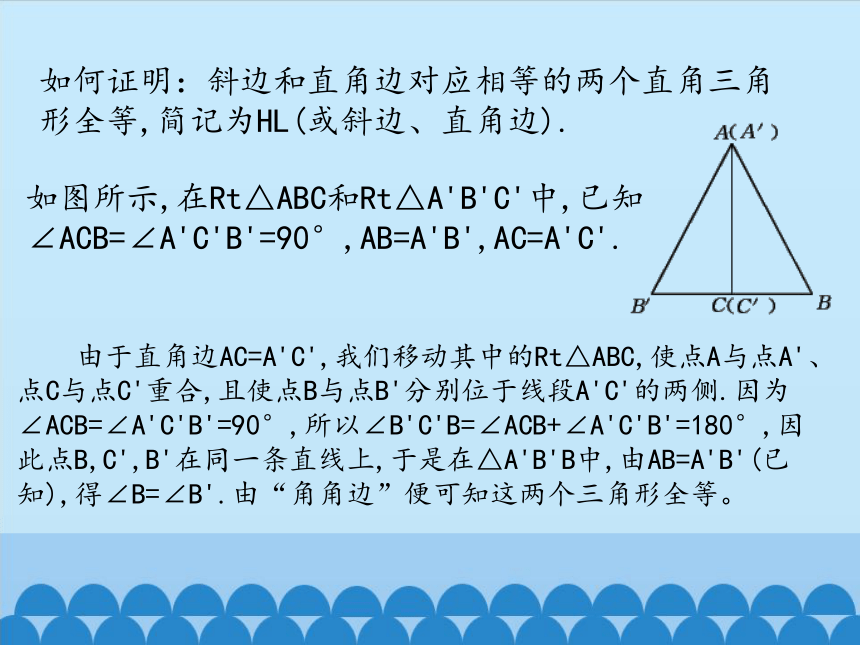
如何证明:斜边和直角边对应相等的两个直角三角形全等,简记为HL(或斜边、直角边).
如图所示,在Rt△ABC和Rt△A'B'C'中,已知∠ACB=∠A'C'B'=90°,AB=A'B',AC=A'C'.
由于直角边AC=A'C',我们移动其中的Rt△ABC,使点A与点A'、点C与点C'重合,且使点B与点B'分别位于线段A'C'的两侧.因为∠ACB=∠A'C'B'=90°,所以∠B'C'B=∠ACB+∠A'C'B'=180°,因此点B,C',B'在同一条直线上,于是在△A'B'B中,由AB=A'B'(已知),得∠B=∠B'.由“角角边”便可知这两个三角形全等。
已知一直角边和斜边,用尺规作直角三角形.
已知:如图所示,线段a,c.
求作:△ABC,使∠C=90°,BC=a,AB=c.
作法:如图所示.
(1)作线段CB=a.
(2)过点C,作MC⊥BC.
(3)以B为圆心,c为半径画弧,交CM于点A.
(4)连接AB.则△ABC即为所求.
分析:首先作出边BC,由∠C为直角可以作出另一直角边所在的射线,由AB=c可以确定点A.
结论:斜边和直角边对应相等的两个直角三角形全等.
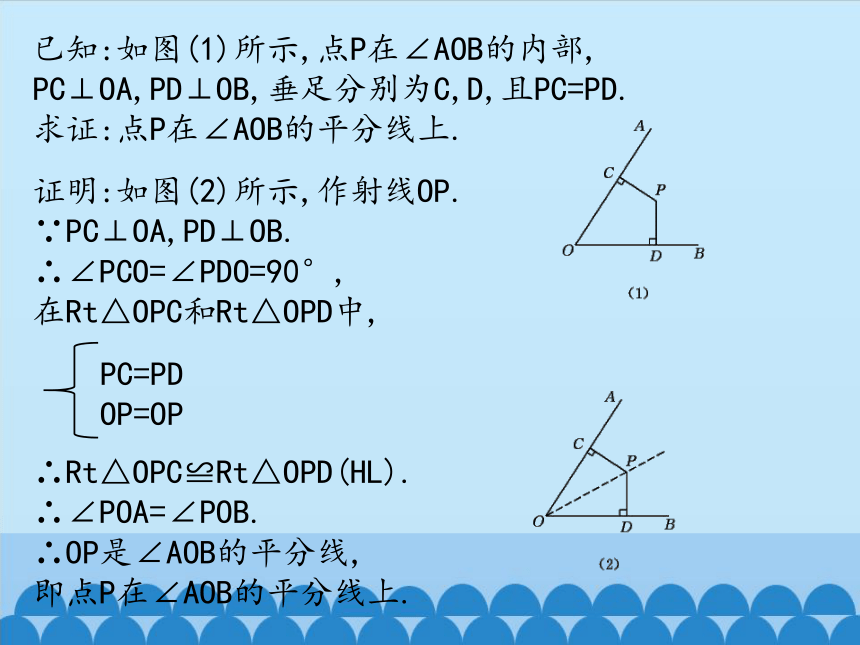
已知:如图(1)所示,点P在∠AOB的内部,
PC⊥OA,PD⊥OB,垂足分别为C,D,且PC=PD.
求证:点P在∠AOB的平分线上.
证明:如图(2)所示,作射线OP.
∵PC⊥OA,PD⊥OB.
∴∠PCO=∠PDO=90°,
在Rt△OPC和Rt△OPD中,
∴Rt△OPC≌Rt△OPD(HL).
∴∠POA=∠POB.
∴OP是∠AOB的平分线,
即点P在∠AOB的平分线上.
PC=PD
OP=OP
思考:这个命题与角平分线的性质定理有什么区别?通过这道题,你能得到怎样的结论?
归纳:角平分线性质定理的逆定理:到角两边距离相等的点在这个角的平分线上.
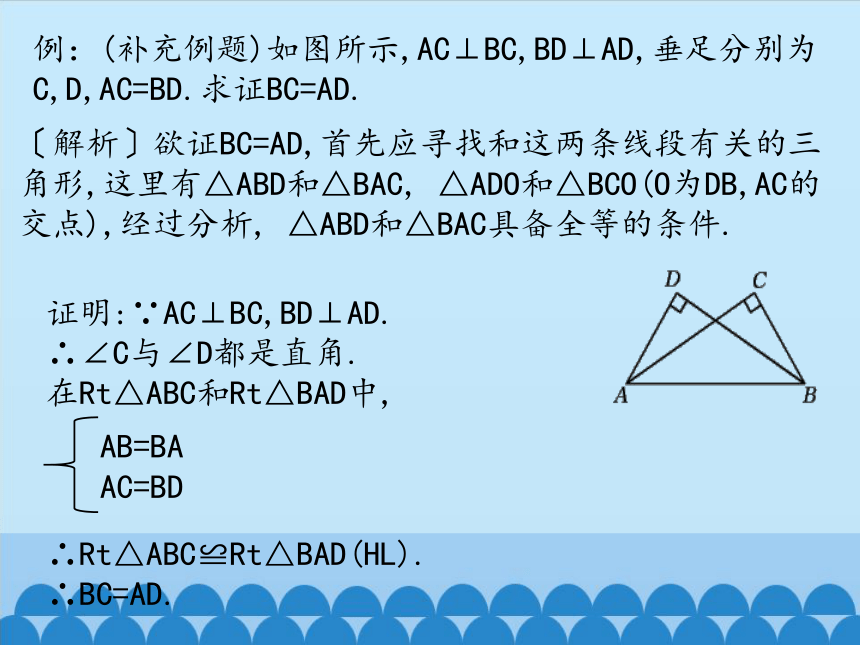
例:(补充例题)如图所示,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD.求证BC=AD.
〔解析〕欲证BC=AD,首先应寻找和这两条线段有关的三角形,这里有△ABD和△BAC,
△ADO和△BCO(O为DB,AC的交点),经过分析,
△ABD和△BAC具备全等的条件.
证明:∵AC⊥BC,BD⊥AD.
∴∠C与∠D都是直角.
在Rt△ABC和Rt△BAD中,
∴Rt△ABC≌Rt△BAD(HL).
∴BC=AD.
AB=BA
AC=BD
想一想:
你能用几种方法判定两个直角三角形全等?
直角三角形是特殊的三角形,所以不仅有一般三角形全等的判定法:SAS,ASA,AAS,SSS,还有直角三角形特殊的判定全等的方法——“HL”.
练一练:
1.如图所示,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由.
2.如图所示,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方面的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
下面是三名同学解决第2题的思考过程,你能明白他们的意思吗?
(2)有一条直角边和斜边对应相等,所以Rt△ABC与Rt△DEF全等.所以∠ABC=∠DEF,所以∠ABC+∠DFE=90°.
(3)在Rt△ABC和Rt△DEF中,BC=EF,AC=DF,所以AB=DE,因此这两个直角三角形是全等的,所以∠ABC=∠DEF,所以∠ABC+∠DFE=90°.
CB=EF
AC=DF
∠CAB=
∠FDE=90°
Rt△ABC≌Rt△DEF
→∠ABC=∠DEF
→∠ABC+∠DFE=90°
课堂小结
斜边和直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).
直角三角形首先是三角形,所以一般三角形全等的判定方法都适合它.同时,直角三角形又是特殊的三角形,有它的特殊性,“HL”定理是直角三角形全等独有的判定方法,所以直角三角形的判定方法最多,使用时应该抓住“直角”这个隐含的已知条件.
检测反馈
1.能判定两个直角三角形全等的条件是
( )
A.一个锐角对应相等
B.两个锐角对应相等
C.一条边对应相等
D.两条边对应相等
D
解析:A.一个锐角对应相等,利用已知的直角相等,可得出另一组锐角相等,但不能证明两个直角三角形全等,故A选项错误;B.两个锐角相等,那么也就是三个角对应相等,但不能证明两个直角三角形全等,故B选项错误;C.一条边对应相等,再加一组直角相等,不能得出两个直角三角形全等,故C选项错误;D.两条边对应相等,若是两条直角边相等,可利用SAS证全等,若一直角边对应相等,一斜边对应相等,利用HL也可证全等,故D选项正确.故选D.
2.如图所示,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD,DF,则图中全等的直角三角形共有
( )
A.3对
B.4对
C.5对
D.6对
B
解析:由E是CD中点,可知DE=EC,由四边形ABCD是矩形,可得AD=BC,AB=CD,∠DCB=∠DCF=90°,
AD∥BF,∴∠DAE=∠EFC,图中全等的直角三角形有:△AED≌△FEC,
△BDC≌△FDC≌△DBA,共4对.故选B.
3.如图所示,用“HL”判定Rt△ABC和Rt△DEF全等的条件是
( )
A.AC=DF,BC=EF
B.∠A=∠D,AB=DE
C.AC=DF,AB=DE
D.∠B=∠E,BC=EF
C
解析:∵在两个直角三角形中,AB,DE是斜边,
∴只有C中,AC=DF,AB=DE符合题意.
4.如图所示,
△ABC中,∠ABC=45°,AD⊥BC于D,点E在AD上,且BE=AC,求证DE=CD.
证明:∵∠ABC=45°,AD⊥BC,
∴AD=BD,∠BDE=∠ADC=90°.
又∵BE=AC,
∴Rt△BDE≌Rt△ADC.∴DE=CD.
解析:由∠ABC=45°,AD⊥BC可得到AD=BD,因为BE=AC,所以Rt△BDE≌Rt△ADC,从而得出DE=CD.
谢
谢
飞快的奔跑,纵情的跳跃,随心所欲的游动,变幻莫测的战术配合,充满激情与韵律的舞步……令人赏心悦目,赞叹不已。
欣赏
思考
我们经常见到的这些身体活动,都有一个共同的特征,是什么呢?
结论
这些身体活动都是人体与地面或其他物体相互作用,使人体在水平或垂直方向上产生的移动。因此,移动是它们的主要特征。
田径运动中的短跑、障碍跑、跳高、跳远,球类运动中的各种跑动、步法移动,健美操、舞蹈中的节律性移动,游泳等,都属于综合性移动技能。综合性移动技能也广泛应用于日常生活中。
综合性移动技能
速度、距离、节奏、时机、方向等是评价移动效果好坏的主要指标。
一点通
运动技能的学习,是一个既充满挑战也充满乐趣的过程。从不会到初步掌握,再到掌握得比较熟练,最后到能够比较自如地运用所学的运用技能,其中的每一点儿进步,都有着无穷的乐趣和成功的喜悦。
综合性移动技能广泛应用于多种运动项目中,如足球、排球、篮球、羽毛球等,同时还有许多民族民间传统运动项目。
影响综合性移动技能发展的主要因素
正确的运动姿势
身体各部位的协调配合
体育活动中发展的综合性移动技能,不仅可以丰富锻炼身体的手段和途径,而且可以对生活和日后工作所需要的操作技能产生积极影响。
影响综合性移动技能发展的主要因素
快速移动中的身体平衡能力
体能、心理因素(兴趣、情绪等)
谢
谢
17.4直角三角形全等的判定
三角形全等的判定方法有哪些?
复习巩固
SSS(三边对应相等的两个三角形全等)
ASA(两角和它们的夹边对应相等的两个三角形全等)
SAS(两边和它们的夹角对应相等的两个三角形全等)
AAS(两角和其中一角的对边对应相等的两个三角形全等)
复习巩固
有哪些边角的组合不能判定两个三角形全等?你能通过画图说明理由吗?
如图(1)所示,已知两条线段(这两条线段长不相等),以长的线段为斜边、短的线段为一条直角边,画一个直角三角形.所有的直角三角形都全等吗?
学习新知
1.画一线段AB,使它等于4cm;
2.画∠EAB=90°;
3.以点B为圆心,以5cm长为半径画弧,交射线AE于点C;
4.连接BC,△ABC即为所求,
如图(2)所示.
如何证明:斜边和直角边对应相等的两个直角三角形全等,简记为HL(或斜边、直角边).
如图所示,在Rt△ABC和Rt△A'B'C'中,已知∠ACB=∠A'C'B'=90°,AB=A'B',AC=A'C'.
由于直角边AC=A'C',我们移动其中的Rt△ABC,使点A与点A'、点C与点C'重合,且使点B与点B'分别位于线段A'C'的两侧.因为∠ACB=∠A'C'B'=90°,所以∠B'C'B=∠ACB+∠A'C'B'=180°,因此点B,C',B'在同一条直线上,于是在△A'B'B中,由AB=A'B'(已知),得∠B=∠B'.由“角角边”便可知这两个三角形全等。
已知一直角边和斜边,用尺规作直角三角形.
已知:如图所示,线段a,c.
求作:△ABC,使∠C=90°,BC=a,AB=c.
作法:如图所示.
(1)作线段CB=a.
(2)过点C,作MC⊥BC.
(3)以B为圆心,c为半径画弧,交CM于点A.
(4)连接AB.则△ABC即为所求.
分析:首先作出边BC,由∠C为直角可以作出另一直角边所在的射线,由AB=c可以确定点A.
结论:斜边和直角边对应相等的两个直角三角形全等.
已知:如图(1)所示,点P在∠AOB的内部,
PC⊥OA,PD⊥OB,垂足分别为C,D,且PC=PD.
求证:点P在∠AOB的平分线上.
证明:如图(2)所示,作射线OP.
∵PC⊥OA,PD⊥OB.
∴∠PCO=∠PDO=90°,
在Rt△OPC和Rt△OPD中,
∴Rt△OPC≌Rt△OPD(HL).
∴∠POA=∠POB.
∴OP是∠AOB的平分线,
即点P在∠AOB的平分线上.
PC=PD
OP=OP
思考:这个命题与角平分线的性质定理有什么区别?通过这道题,你能得到怎样的结论?
归纳:角平分线性质定理的逆定理:到角两边距离相等的点在这个角的平分线上.
例:(补充例题)如图所示,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD.求证BC=AD.
〔解析〕欲证BC=AD,首先应寻找和这两条线段有关的三角形,这里有△ABD和△BAC,
△ADO和△BCO(O为DB,AC的交点),经过分析,
△ABD和△BAC具备全等的条件.
证明:∵AC⊥BC,BD⊥AD.
∴∠C与∠D都是直角.
在Rt△ABC和Rt△BAD中,
∴Rt△ABC≌Rt△BAD(HL).
∴BC=AD.
AB=BA
AC=BD
想一想:
你能用几种方法判定两个直角三角形全等?
直角三角形是特殊的三角形,所以不仅有一般三角形全等的判定法:SAS,ASA,AAS,SSS,还有直角三角形特殊的判定全等的方法——“HL”.
练一练:
1.如图所示,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由.
2.如图所示,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方面的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
下面是三名同学解决第2题的思考过程,你能明白他们的意思吗?
(2)有一条直角边和斜边对应相等,所以Rt△ABC与Rt△DEF全等.所以∠ABC=∠DEF,所以∠ABC+∠DFE=90°.
(3)在Rt△ABC和Rt△DEF中,BC=EF,AC=DF,所以AB=DE,因此这两个直角三角形是全等的,所以∠ABC=∠DEF,所以∠ABC+∠DFE=90°.
CB=EF
AC=DF
∠CAB=
∠FDE=90°
Rt△ABC≌Rt△DEF
→∠ABC=∠DEF
→∠ABC+∠DFE=90°
课堂小结
斜边和直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).
直角三角形首先是三角形,所以一般三角形全等的判定方法都适合它.同时,直角三角形又是特殊的三角形,有它的特殊性,“HL”定理是直角三角形全等独有的判定方法,所以直角三角形的判定方法最多,使用时应该抓住“直角”这个隐含的已知条件.
检测反馈
1.能判定两个直角三角形全等的条件是
( )
A.一个锐角对应相等
B.两个锐角对应相等
C.一条边对应相等
D.两条边对应相等
D
解析:A.一个锐角对应相等,利用已知的直角相等,可得出另一组锐角相等,但不能证明两个直角三角形全等,故A选项错误;B.两个锐角相等,那么也就是三个角对应相等,但不能证明两个直角三角形全等,故B选项错误;C.一条边对应相等,再加一组直角相等,不能得出两个直角三角形全等,故C选项错误;D.两条边对应相等,若是两条直角边相等,可利用SAS证全等,若一直角边对应相等,一斜边对应相等,利用HL也可证全等,故D选项正确.故选D.
2.如图所示,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD,DF,则图中全等的直角三角形共有
( )
A.3对
B.4对
C.5对
D.6对
B
解析:由E是CD中点,可知DE=EC,由四边形ABCD是矩形,可得AD=BC,AB=CD,∠DCB=∠DCF=90°,
AD∥BF,∴∠DAE=∠EFC,图中全等的直角三角形有:△AED≌△FEC,
△BDC≌△FDC≌△DBA,共4对.故选B.
3.如图所示,用“HL”判定Rt△ABC和Rt△DEF全等的条件是
( )
A.AC=DF,BC=EF
B.∠A=∠D,AB=DE
C.AC=DF,AB=DE
D.∠B=∠E,BC=EF
C
解析:∵在两个直角三角形中,AB,DE是斜边,
∴只有C中,AC=DF,AB=DE符合题意.
4.如图所示,
△ABC中,∠ABC=45°,AD⊥BC于D,点E在AD上,且BE=AC,求证DE=CD.
证明:∵∠ABC=45°,AD⊥BC,
∴AD=BD,∠BDE=∠ADC=90°.
又∵BE=AC,
∴Rt△BDE≌Rt△ADC.∴DE=CD.
解析:由∠ABC=45°,AD⊥BC可得到AD=BD,因为BE=AC,所以Rt△BDE≌Rt△ADC,从而得出DE=CD.
谢
谢
飞快的奔跑,纵情的跳跃,随心所欲的游动,变幻莫测的战术配合,充满激情与韵律的舞步……令人赏心悦目,赞叹不已。
欣赏
思考
我们经常见到的这些身体活动,都有一个共同的特征,是什么呢?
结论
这些身体活动都是人体与地面或其他物体相互作用,使人体在水平或垂直方向上产生的移动。因此,移动是它们的主要特征。
田径运动中的短跑、障碍跑、跳高、跳远,球类运动中的各种跑动、步法移动,健美操、舞蹈中的节律性移动,游泳等,都属于综合性移动技能。综合性移动技能也广泛应用于日常生活中。
综合性移动技能
速度、距离、节奏、时机、方向等是评价移动效果好坏的主要指标。
一点通
运动技能的学习,是一个既充满挑战也充满乐趣的过程。从不会到初步掌握,再到掌握得比较熟练,最后到能够比较自如地运用所学的运用技能,其中的每一点儿进步,都有着无穷的乐趣和成功的喜悦。
综合性移动技能广泛应用于多种运动项目中,如足球、排球、篮球、羽毛球等,同时还有许多民族民间传统运动项目。
影响综合性移动技能发展的主要因素
正确的运动姿势
身体各部位的协调配合
体育活动中发展的综合性移动技能,不仅可以丰富锻炼身体的手段和途径,而且可以对生活和日后工作所需要的操作技能产生积极影响。
影响综合性移动技能发展的主要因素
快速移动中的身体平衡能力
体能、心理因素(兴趣、情绪等)
谢
谢
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
