浙江省宁波市重点中学2022届高三上学期返校考试数学试题(Word版含答案)
文档属性
| 名称 | 浙江省宁波市重点中学2022届高三上学期返校考试数学试题(Word版含答案) | 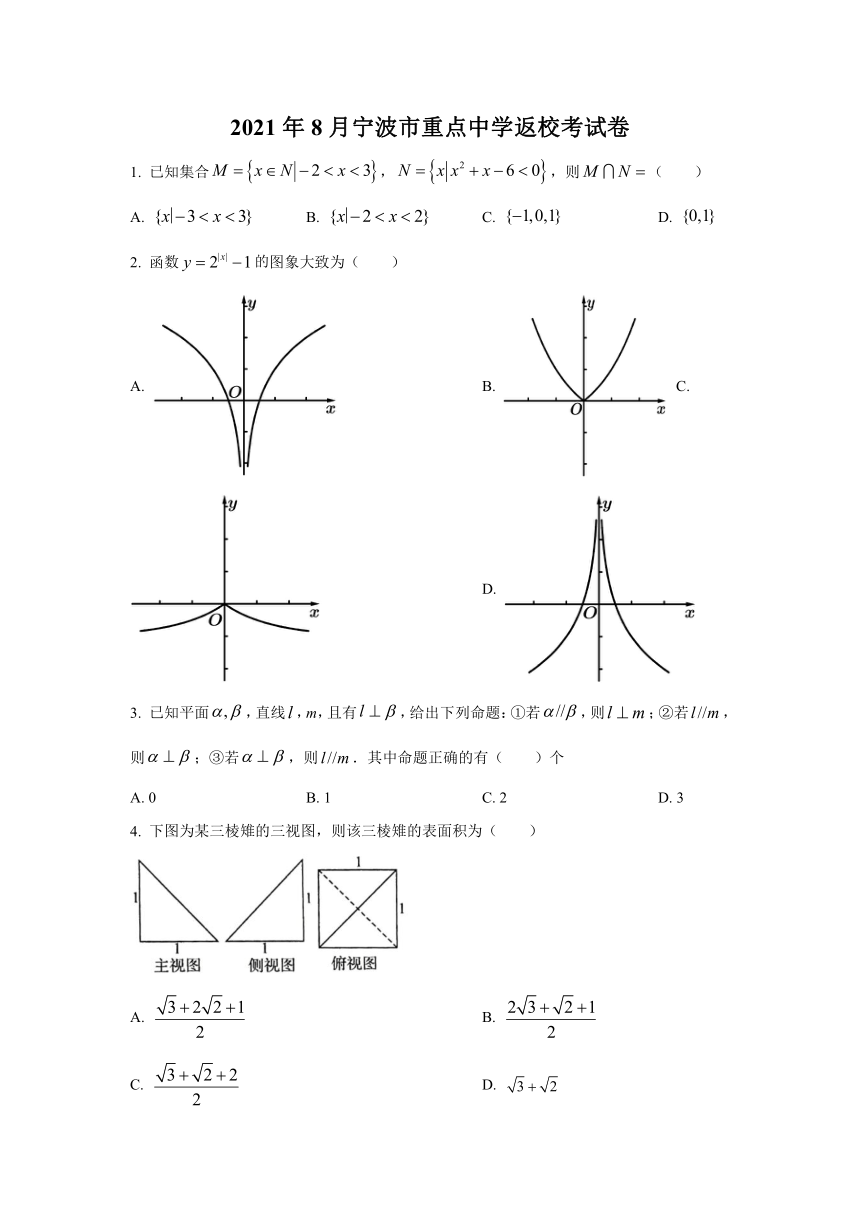 | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 12:41:41 | ||
图片预览




文档简介
2021年8月宁波市重点中学返校考试卷
1.
已知集合,,则(
)
A.
B.
C.
D.
2.
函数图象大致为(
)
A.
B.
C.
D.
3.
已知平面,直线,m,且有,给出下列命题:①若,则;②若,则;③若,则.其中命题正确的有(
)个
A.
0
B.
1
C.
2
D.
3
4.
下图为某三棱雉的三视图,则该三棱雉的表面积为(
)
A.
B.
C.
D.
5.
设实数满足条件,则的取值范围是(
)
A.
B.
C.
D.
6.
已知为常数,若展开式中的系数为,则(
)
A.
B.
C.
1
D.
2
7.
已知定点,动点Q在圆O:上,PQ的垂直平分线交直线
OQ于M点,若动点M的轨迹是双曲线,则m的值可以是(
)
A.
2
B.
3
C.
4
D.
5
8.
已知甲、乙两人进行五局球赛,甲每局获胜的概率是,且各局的胜负相互独立,已知
甲胜一局的奖金为10元,设甲所获得的资金总额为X元,则甲所获得奖金总额的方差(
)
A.
120
B.
240
C.
360
D.
480
9
已知,且,对任意均有,则(
)
A.
B.
C.
D.
10.
若函数的定义域为,满足,,都有,则关于的不等式的解集为(
)
A.
B.
C.
D.
11.
设复数(其中为虚数单位),则的虚部是_________,_________.
12.
抛物线的焦点到双曲线的一条渐近线的距离是,则双曲线的实轴长是__________,离心率是__________.
13.
若,且,当且仅当_________,
________时,取得最小值.
14.
已知对任意恒成立,且,,则___________;___________.
15.
用0,1,2,3,4,5组成无重复数字的六位偶数,若有且仅有2个奇数相邻,则这样的六位数共有___________个.
16.
设函数,若不等式对任意恒成立,则最大值为______________.
17.
设数列的前项和为,,(),(,).且?均为等差数列,则_________.
18.
在中,角,,所对的边分别是,,,.
(1)证明:;
(2)求角的取值范围.
19.
如图,已知四边形是菱形,是边长为的正三角形,为的中点,又
(1)求证:;
(2)求直线与平面所成角的正弦值.
20.
已知正项数列的前n项和为,且,.
(1)求数列的通项公式;
(2)若为等差数列,求证:.
21.
如图,已知,直线,是平面上的动点,过点P作l的垂线,垂足为点Q,且.
(1)求动点P轨迹C的方程;
(2)过点F的直线交轨迹C于A、B两点,交直线l于点M;
①已知,求的值;
②求的最小值.
22.
已知函数f(x)=ex+1-alnax+a(a>0).
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若关于x的不等式f(x)>0恒成立,求实数a的取值范围.
2021年8月宁波市重点中学返校考试卷
答案版
1.
已知集合,,则(
)
A.
B.
C.
D.
答案:D
2.
函数图象大致为(
)
A.
B.
C.
D.
答案:B
3.
已知平面,直线,m,且有,给出下列命题:①若,则;②若,则;③若,则.其中命题正确的有(
)个
A.
0
B.
1
C.
2
D.
3
答案:A
4.
下图为某三棱雉的三视图,则该三棱雉的表面积为(
)
A.
B.
C.
D.
答案:A
5.
设实数满足条件,则的取值范围是(
)
A.
B.
C.
D.
答案:C
6.
已知为常数,若展开式中的系数为,则(
)
A.
B.
C.
1
D.
2
答案:B
7.
已知定点,动点Q在圆O:上,PQ的垂直平分线交直线
OQ于M点,若动点M的轨迹是双曲线,则m的值可以是(
)
A.
2
B.
3
C.
4
D.
5
答案:D
8.
已知甲、乙两人进行五局球赛,甲每局获胜的概率是,且各局的胜负相互独立,已知
甲胜一局的奖金为10元,设甲所获得的资金总额为X元,则甲所获得奖金总额的方差(
)
A.
120
B.
240
C.
360
D.
480
答案:A
9
已知,且,对任意均有,则(
)
A.
B.
C.
D.
答案:B
10.
若函数的定义域为,满足,,都有,则关于的不等式的解集为(
)
A.
B.
C.
D.
答案:A
11.
设复数(其中为虚数单位),则的虚部是_________,_________.
答案:
①.
1
②.
0
12.
抛物线的焦点到双曲线的一条渐近线的距离是,则双曲线的实轴长是__________,离心率是__________.
答案:
①.
②.
13.
若,且,当且仅当_________,
________时,取得最小值.
答案:
①.
4
②.
2
14.
已知对任意恒成立,且,,则___________;___________.
答案:
①.
②.
15.
用0,1,2,3,4,5组成无重复数字的六位偶数,若有且仅有2个奇数相邻,则这样的六位数共有___________个.
答案:192
16.
设函数,若不等式对任意恒成立,则最大值为______________.
答案:
17.
设数列的前项和为,,(),(,).且?均为等差数列,则_________.
答案:
18.
在中,角,,所对的边分别是,,,.
(1)证明:;
(2)求角的取值范围.
答案:(1)证明见解析;(2)
19.
如图,已知四边形是菱形,是边长为的正三角形,为的中点,又
(1)求证:;
(2)求直线与平面所成角的正弦值.
答案:(1)证明见解析;(2).
20.
已知正项数列的前n项和为,且,.
(1)求数列的通项公式;
(2)若为等差数列,求证:.
答案:(1);(2)证明过程见解析.
21.
如图,已知,直线,是平面上的动点,过点P作l的垂线,垂足为点Q,且.
(1)求动点P轨迹C的方程;
(2)过点F的直线交轨迹C于A、B两点,交直线l于点M;
①已知,求的值;
②求的最小值.
答案:(1);(2)①;②.
22.
已知函数f(x)=ex+1-alnax+a(a>0).
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若关于x的不等式f(x)>0恒成立,求实数a的取值范围.
答案:(1)
(e2-1)x-y-2=0.(2)
(0,e2)
1.
已知集合,,则(
)
A.
B.
C.
D.
2.
函数图象大致为(
)
A.
B.
C.
D.
3.
已知平面,直线,m,且有,给出下列命题:①若,则;②若,则;③若,则.其中命题正确的有(
)个
A.
0
B.
1
C.
2
D.
3
4.
下图为某三棱雉的三视图,则该三棱雉的表面积为(
)
A.
B.
C.
D.
5.
设实数满足条件,则的取值范围是(
)
A.
B.
C.
D.
6.
已知为常数,若展开式中的系数为,则(
)
A.
B.
C.
1
D.
2
7.
已知定点,动点Q在圆O:上,PQ的垂直平分线交直线
OQ于M点,若动点M的轨迹是双曲线,则m的值可以是(
)
A.
2
B.
3
C.
4
D.
5
8.
已知甲、乙两人进行五局球赛,甲每局获胜的概率是,且各局的胜负相互独立,已知
甲胜一局的奖金为10元,设甲所获得的资金总额为X元,则甲所获得奖金总额的方差(
)
A.
120
B.
240
C.
360
D.
480
9
已知,且,对任意均有,则(
)
A.
B.
C.
D.
10.
若函数的定义域为,满足,,都有,则关于的不等式的解集为(
)
A.
B.
C.
D.
11.
设复数(其中为虚数单位),则的虚部是_________,_________.
12.
抛物线的焦点到双曲线的一条渐近线的距离是,则双曲线的实轴长是__________,离心率是__________.
13.
若,且,当且仅当_________,
________时,取得最小值.
14.
已知对任意恒成立,且,,则___________;___________.
15.
用0,1,2,3,4,5组成无重复数字的六位偶数,若有且仅有2个奇数相邻,则这样的六位数共有___________个.
16.
设函数,若不等式对任意恒成立,则最大值为______________.
17.
设数列的前项和为,,(),(,).且?均为等差数列,则_________.
18.
在中,角,,所对的边分别是,,,.
(1)证明:;
(2)求角的取值范围.
19.
如图,已知四边形是菱形,是边长为的正三角形,为的中点,又
(1)求证:;
(2)求直线与平面所成角的正弦值.
20.
已知正项数列的前n项和为,且,.
(1)求数列的通项公式;
(2)若为等差数列,求证:.
21.
如图,已知,直线,是平面上的动点,过点P作l的垂线,垂足为点Q,且.
(1)求动点P轨迹C的方程;
(2)过点F的直线交轨迹C于A、B两点,交直线l于点M;
①已知,求的值;
②求的最小值.
22.
已知函数f(x)=ex+1-alnax+a(a>0).
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若关于x的不等式f(x)>0恒成立,求实数a的取值范围.
2021年8月宁波市重点中学返校考试卷
答案版
1.
已知集合,,则(
)
A.
B.
C.
D.
答案:D
2.
函数图象大致为(
)
A.
B.
C.
D.
答案:B
3.
已知平面,直线,m,且有,给出下列命题:①若,则;②若,则;③若,则.其中命题正确的有(
)个
A.
0
B.
1
C.
2
D.
3
答案:A
4.
下图为某三棱雉的三视图,则该三棱雉的表面积为(
)
A.
B.
C.
D.
答案:A
5.
设实数满足条件,则的取值范围是(
)
A.
B.
C.
D.
答案:C
6.
已知为常数,若展开式中的系数为,则(
)
A.
B.
C.
1
D.
2
答案:B
7.
已知定点,动点Q在圆O:上,PQ的垂直平分线交直线
OQ于M点,若动点M的轨迹是双曲线,则m的值可以是(
)
A.
2
B.
3
C.
4
D.
5
答案:D
8.
已知甲、乙两人进行五局球赛,甲每局获胜的概率是,且各局的胜负相互独立,已知
甲胜一局的奖金为10元,设甲所获得的资金总额为X元,则甲所获得奖金总额的方差(
)
A.
120
B.
240
C.
360
D.
480
答案:A
9
已知,且,对任意均有,则(
)
A.
B.
C.
D.
答案:B
10.
若函数的定义域为,满足,,都有,则关于的不等式的解集为(
)
A.
B.
C.
D.
答案:A
11.
设复数(其中为虚数单位),则的虚部是_________,_________.
答案:
①.
1
②.
0
12.
抛物线的焦点到双曲线的一条渐近线的距离是,则双曲线的实轴长是__________,离心率是__________.
答案:
①.
②.
13.
若,且,当且仅当_________,
________时,取得最小值.
答案:
①.
4
②.
2
14.
已知对任意恒成立,且,,则___________;___________.
答案:
①.
②.
15.
用0,1,2,3,4,5组成无重复数字的六位偶数,若有且仅有2个奇数相邻,则这样的六位数共有___________个.
答案:192
16.
设函数,若不等式对任意恒成立,则最大值为______________.
答案:
17.
设数列的前项和为,,(),(,).且?均为等差数列,则_________.
答案:
18.
在中,角,,所对的边分别是,,,.
(1)证明:;
(2)求角的取值范围.
答案:(1)证明见解析;(2)
19.
如图,已知四边形是菱形,是边长为的正三角形,为的中点,又
(1)求证:;
(2)求直线与平面所成角的正弦值.
答案:(1)证明见解析;(2).
20.
已知正项数列的前n项和为,且,.
(1)求数列的通项公式;
(2)若为等差数列,求证:.
答案:(1);(2)证明过程见解析.
21.
如图,已知,直线,是平面上的动点,过点P作l的垂线,垂足为点Q,且.
(1)求动点P轨迹C的方程;
(2)过点F的直线交轨迹C于A、B两点,交直线l于点M;
①已知,求的值;
②求的最小值.
答案:(1);(2)①;②.
22.
已知函数f(x)=ex+1-alnax+a(a>0).
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若关于x的不等式f(x)>0恒成立,求实数a的取值范围.
答案:(1)
(e2-1)x-y-2=0.(2)
(0,e2)
同课章节目录
