2012新课标同步导学高一数学练习:3.3.1(北师大版必修4)
文档属性
| 名称 | 2012新课标同步导学高一数学练习:3.3.1(北师大版必修4) | 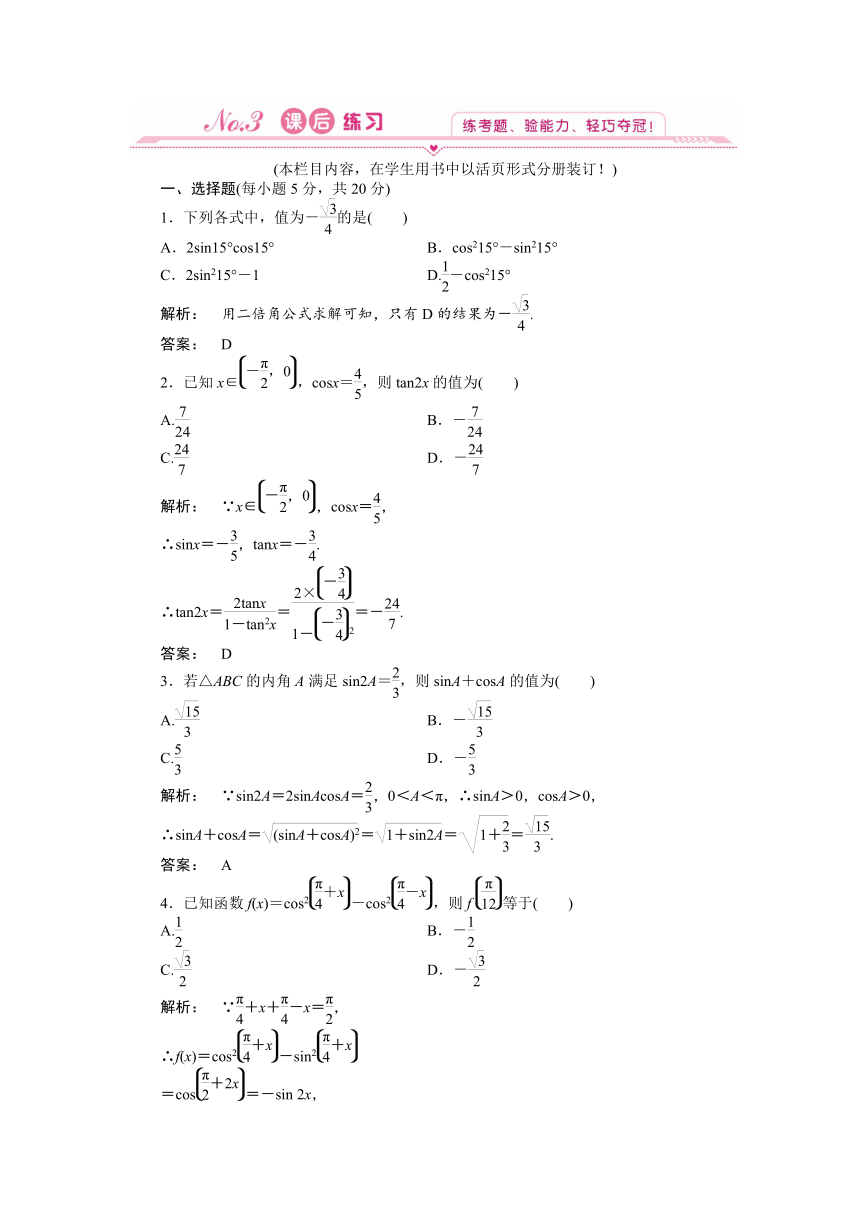 | |
| 格式 | zip | ||
| 文件大小 | 69.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-24 22:09:10 | ||
图片预览
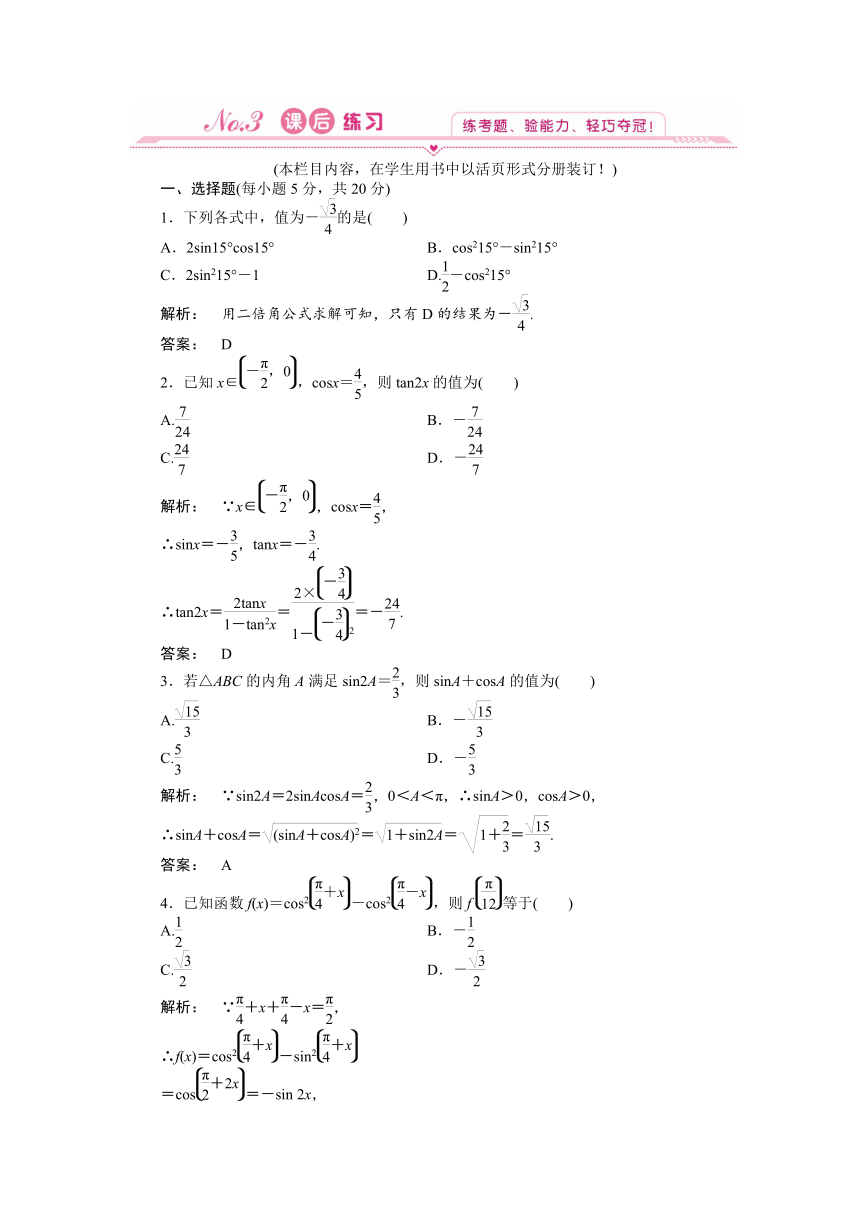
文档简介
(本栏目内容,在学生用书中以活页形式分册装订!)
一、选择题(每小题5分,共20分)
1.下列各式中,值为-的是( )
A.2sin15°cos15° B.cos215°-sin215°
C.2sin215°-1 D.-cos215°
解析: 用二倍角公式求解可知,只有D的结果为-.
答案: D
2.已知x∈,cosx=,则tan2x的值为( )
A. B.-
C. D.-
解析: ∵x∈,cosx=,
∴sinx=-,tanx=-.
∴tan2x===-.
答案: D
3.若△ABC的内角A满足sin2A=,则sinA+cosA的值为( )
A. B.-
C. D.-
解析: ∵sin2A=2sinAcosA=,0<A<π,∴sinA>0,cosA>0,
∴sinA+cosA====.
答案: A
4.已知函数f(x)=cos2-cos2,则f等于( )
A. B.-
C. D.-
解析: ∵+x+-x=,
∴f(x)=cos2-sin2
=cos=-sin 2x,
∴f=-.
答案: B
二、填空题(每小题5分,共10分)
5.已知tan =2,则tan α的值为________,tan 的值为________.
解析: tan α=tan==-,
进而有tan==-.
答案: - -
6.函数y=sinx·(sinx+cosx)(x∈R)的最大值是________.
解析: y=sinx·(sinx+cosx)=sin2x+sinxcosx
=+sin2x=+sin≤.
答案:
三、解答题(每小题10分,共20分)
7.已知sin α=cos 2α,α∈(0,),求sin 2α.
解析: ∵sin α=1-2sin2α,即2sin2α+sin α-1=0,
∴sin α=-1或sin α=.
又∵α∈(0,),∴sin α=,α=.
∴cos α=.∴sin 2α=2××=.
8.求-sin10°的值.
解析: 原式=-2sin10°·
=-2sin10°·
=-2cos10°=
==
??☆☆☆
9.(10分)已知:tan(π+α)=-.tan(α+β)=.
(1)求tan(α+β)的值;
(2)求tan β的值.
解析: (1)∵tan(π+α)=-
∴tan α=-
∵tan(α+β)=
=
=
=
=
==
(2)∵tan β=tan[(α+β)-α]
=
==.
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
一、选择题(每小题5分,共20分)
1.下列各式中,值为-的是( )
A.2sin15°cos15° B.cos215°-sin215°
C.2sin215°-1 D.-cos215°
解析: 用二倍角公式求解可知,只有D的结果为-.
答案: D
2.已知x∈,cosx=,则tan2x的值为( )
A. B.-
C. D.-
解析: ∵x∈,cosx=,
∴sinx=-,tanx=-.
∴tan2x===-.
答案: D
3.若△ABC的内角A满足sin2A=,则sinA+cosA的值为( )
A. B.-
C. D.-
解析: ∵sin2A=2sinAcosA=,0<A<π,∴sinA>0,cosA>0,
∴sinA+cosA====.
答案: A
4.已知函数f(x)=cos2-cos2,则f等于( )
A. B.-
C. D.-
解析: ∵+x+-x=,
∴f(x)=cos2-sin2
=cos=-sin 2x,
∴f=-.
答案: B
二、填空题(每小题5分,共10分)
5.已知tan =2,则tan α的值为________,tan 的值为________.
解析: tan α=tan==-,
进而有tan==-.
答案: - -
6.函数y=sinx·(sinx+cosx)(x∈R)的最大值是________.
解析: y=sinx·(sinx+cosx)=sin2x+sinxcosx
=+sin2x=+sin≤.
答案:
三、解答题(每小题10分,共20分)
7.已知sin α=cos 2α,α∈(0,),求sin 2α.
解析: ∵sin α=1-2sin2α,即2sin2α+sin α-1=0,
∴sin α=-1或sin α=.
又∵α∈(0,),∴sin α=,α=.
∴cos α=.∴sin 2α=2××=.
8.求-sin10°的值.
解析: 原式=-2sin10°·
=-2sin10°·
=-2cos10°=
==
??☆☆☆
9.(10分)已知:tan(π+α)=-.tan(α+β)=.
(1)求tan(α+β)的值;
(2)求tan β的值.
解析: (1)∵tan(π+α)=-
∴tan α=-
∵tan(α+β)=
=
=
=
=
==
(2)∵tan β=tan[(α+β)-α]
=
==.
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
