2012新课标同步导学高一数学练习:模块综合测评(B)(人教A版必修3)
文档属性
| 名称 | 2012新课标同步导学高一数学练习:模块综合测评(B)(人教A版必修3) |  | |
| 格式 | zip | ||
| 文件大小 | 257.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-24 22:11:12 | ||
图片预览



文档简介
模块综合测评(B)
(本栏目内容,在学生用书中以活页形式分册装订!)
(时间120分钟,满分150分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.用“更相减损术”求225与135的最大公约数为( )
A.45 B.5
C.9 D.15
解析: 225-135=90,135-90=45,90-45=45,所以选A.
答案: A
2.某社区有500个家庭,其中高收入家庭125户,中等收入家庭280户,低收入家庭95户,为了调查社会购买力的某项指标,要从中抽取一个容量为100户的样本,记作①.某学校高一年级有12名女排运动员,要从中选出3人调查学习负担情况,记作②.那么完成上述两项调查应采用的抽样方法是( )
A.①用随机抽样法,②用系统抽样法
B.①用分层抽样法,②用随机抽样法
C.①用系统抽样法,②用分层抽样法
D.①用分层抽样法,②用系统抽样法
解析: ①中具有明显的分层,适合用分层抽样法,②中总体容量,样本容量都较小,适合用随机抽样法.故选B.
答案: B
3.在一次随机试验中,彼此互斥的事件A、B、C、D的概率分别是0.2、0.2、0.3、0.3,则下列说法正确的是( )
A.A+B与C是互斥事件,也是对立事件
B.B+C与D是互斥事件,也是对立事件
C.A+C与B+D是互斥事件,但不是对立事件
D.A与B+C+D是互斥事件,也是对立事件
解析: ∵A、B、C、D是互斥事件.
且P(A+B+C+D)=1
∴A与B+C+D是互斥事件,也是对立事件.
答案: D
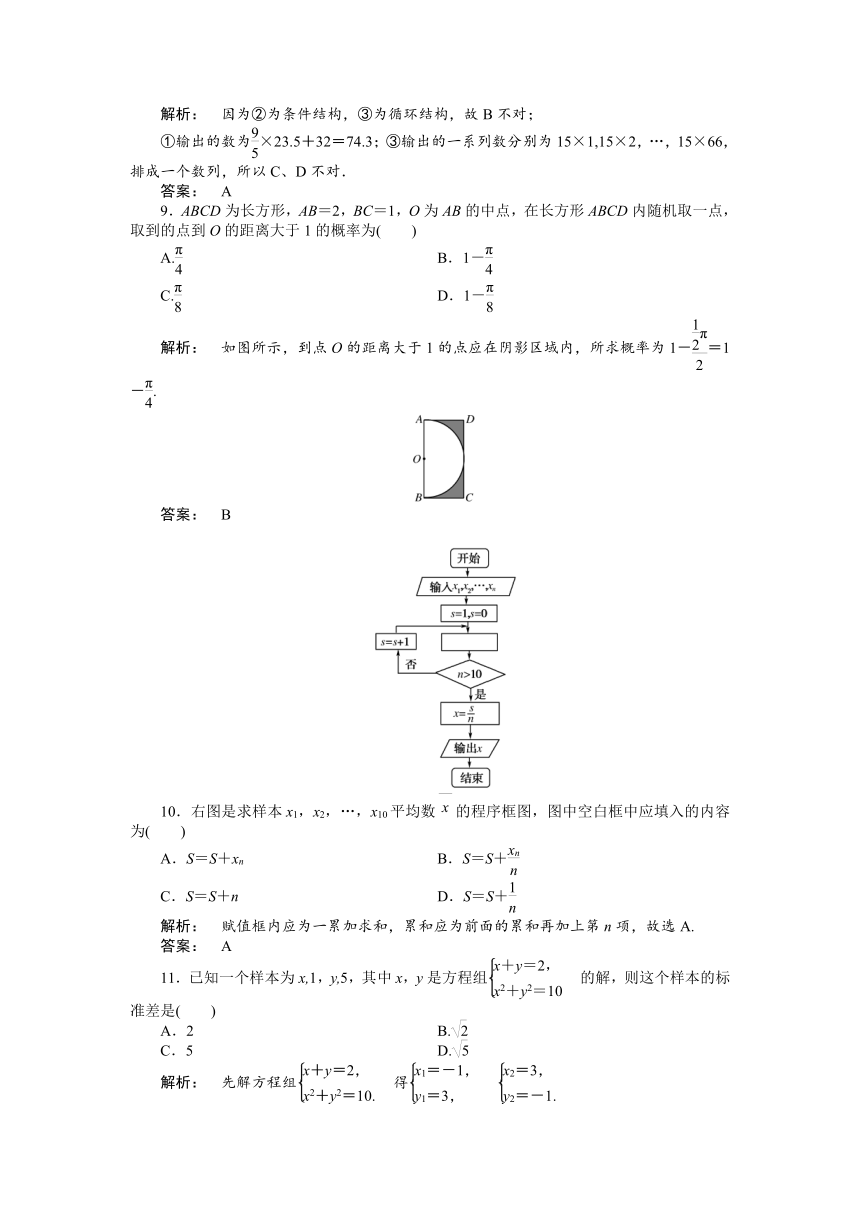
4.在佛山市禅城区和南海区打的士收费办法如下:不超过2千米收7元,超过2千米的里程每千米收2.6元,另每车次超过2千米收燃油附加费1元(其他因素不考虑).相应收费系统的程序框图如图所示,则①处应填( )
A.y=7+2.6x B.y=8+2.6x
C.y=7+2.6(x-2) D.y=8+2.6(x-2)
解析: 当x>2时,按y=8+2.6(x-2)收费;
当x≤2时,收费7元.
答案: D
5.为了解某县甲、乙、丙三所学校高三数学模拟的考试成绩,采取分层抽样方法,从甲校的1 260份试卷、乙校的720份试卷、丙校的900份试卷中进行抽样调研.如果从丙校的900份试卷中抽取了45份试卷,那么这次调研共抽查的试卷份数为( )
A.88 B.99
C.144 D.63
解析: 从丙校的900份试卷中抽取了45份试卷,说明抽样比是=,所以这次调研共抽查的试卷份数为
(1 260+720+900)×=144.
答案: C
6.观察新生婴儿的体重,其频率分布直方图如下图所示,则新生婴儿体重在[2 700,3 000)的频率为( )
A.0.3 B.0.001
C.0.2 D.0.1
解析: 0.001×300=0.3,故选A.
答案: A
7.把二进制(1 101)2化为五进制数的结果是( )
A.(32)5 B.(30)5
C.(23)5 D.(31)5
解析: (1 101)2=1×23+1×22+0×21+1×20=13
∴13=(23)5.故选C.
答案: C
8.给出①②③三个程序框图如下图,下列说法正确的是( )
A.②为条件结构,③为循环结构
B.①为顺序结构,②为循环结构,③为条件结构
C.①输出的结果为35
D.③输出的a表示比66小的15的倍数中的最大数
解析: 因为②为条件结构,③为循环结构,故B不对;
①输出的数为×23.5+32=74.3;③输出的一系列数分别为15×1,15×2,…,15×66,排成一个数列,所以C、D不对.
答案: A
9.ABCD为长方形,AB=2,BC=1,O为AB的中点,在长方形ABCD内随机取一点,取到的点到O的距离大于1的概率为( )
A. B.1-
C. D.1-
解析: 如图所示,到点O的距离大于1的点应在阴影区域内,所求概率为1-=1-.
答案: B
10.右图是求样本x1,x2,…,x10平均数的程序框图,图中空白框中应填入的内容为( )
A.S=S+xn B.S=S+
C.S=S+n D.S=S+
解析: 赋值框内应为一累加求和,累和应为前面的累和再加上第n项,故选A.
答案: A
11.已知一个样本为x,1,y,5,其中x,y是方程组的解,则这个样本的标准差是( )
A.2 B.
C.5 D.
解析: 先解方程组得
当时,这个样本为-1,1,3,5.
先求其平均数:=×(-1+1+3+5)=2.
再根据样本标准差的公式,求标准差:
s=
=
==.
当时,同理可得标准差为,因此应选D.
答案: D
12.设集合A={1,2},B={1,2,3},分别从集合A和B中随机取一个数a和b,确定平面上的一个点P(a,b),记“点P(a,b)落在直线x+y=n上”为事件Cn(2≤n≤5,n∈N),且事件Cn的概率最大,则n的所有可能值为( )
A.3 B.4
C.3和4 D.2和5
解析: 点P的所有可能值为(1,1),(1,2),(1,3),(2,1),(2,2),(2,3).点P(a,b)落在直线x+y=n上(2≤n≤5,n∈N),且事件Cn的概率最大.当n=3时,P点可能是(1,2),(2,1),当n=4时,P点可能是(1,3),(2,2),即事件C3、C4的概率最大,故选D.
答案: D
二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中的横线上)
13.假设要抽查某种品牌的850颗种子的发牙率,抽取60粒进行实验,利用随机数表抽取种子时,先将850颗种子按001,002,…,850进行编号,如果从随机数表第9行第8列的数4开始向右读,请你依次写出最先检测的4颗种子的编号分别是429,786,________,078.(在横线上填上所缺的种子编号)
(下面摘取了随机数表第7行至第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74
47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50
71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07
44 38 15 51 00 13 42 99 66 02 79 54
解析: 根据随机数表法的读数规则可知4颗种子的编号应为429,786,456,078.
答案: 456
14.将一个总数为A、B、C三层,其个体数之比为5∶3∶2.若用分层抽样方法抽取容量为100的样本,则应从C中抽取________个个体.
解析: C层占总体的=,所以容量为100的样本中,C层所占个体有100×=20(个).
答案: 20
15.(2011·江西高考)如图所示是某算法的程序框图,则程序运行后输出的结果是________.
解析: 第一次进入判断框前n=1,s=0+(-1)1+1=0;
第二次进入判断框前n=2,s=0+(-1)2+2=3;
第三次进入判断框前n=3,s=3+(-1)3+3=5;
第四次进入判断框前n=4,s=5+(-1)4+4=10.
答案: 10
16.某化工厂为预测某产品的回收率y,需要研究它和原料有效成分含量x之间的相关关系.现取了8对观察值,计算得i=52,i=228,=478,iyi=1 849,则y关于x的回归方程是________.
解析: 由=及=- ,各=11.47+2.62x.
答案: =11.47+2.62x
三、解答题(本大题共6小题,共74分.解答时应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分12分)如图是为解决某个问题而绘制的程序框图,仔细分析各图框内的内容及图框之间的关系,回答下面的问题:
(1)图框②中y1=ax+b的含义是什么?
(2)该程序框图解决的是怎样的一个问题?
(3)若最终输出的结果是y1=3,y2=-2.当x取5时输出的结果 5a+b的值应该是多大?
(4)在(3)的前提下,输入的x值越大,输出的ax+b是不是越大?为什么?
解析: (1)图框②中y1=ax+b的含义:该图框在执行①的前提下,即当x=2时计算ax+b的值,并把这个值赋给y1.
(2)该程序框图解决的是求函数f(x)=ax+b的函数值的问题.其中输入的是自变量x的值,输出的是x对应的函数值.
(3)y1=3,即2a+b=3.③
y2=-2,即-3a+b=-2.④
由③④,得a=1,b=1.
∴f(x)=x+1.
∴当x取5时,f(5)=5a+b=5×1+1=6.
(4)输入的x值越大,输出的函数值ax+b越大,因为f(x)=x+1在R上是增函数.
18.(本小题满分12分)已知集合A={-9,-7,-5,-3,-1,0,2,4,6,8},在平面直角坐标系中,点(x,y)的坐标x∈A,y∈A,x≠y,求:
(1)点(x,y)不在x轴上的概率;
(2)点(x,y)正好在第二象限的概率.
解析: 点(x,y)中,x∈A,y∈A,且x≠y,共能组成90个点.
(1)B为“点不在x轴上”,即y≠0,去掉9个点,还余81个点,所以P(B)==.
(2)C为“点在第二象限”,即x<0,y>0,共有20个点,
所以P(C)==.
19.在某次测验中,有6位同学的平均成绩为75分,用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
编号n 1 2 3 4 5
成绩xn 70 76 72 70 72
(1)求第6位同学的成绩x6,及这6位同学成绩的标准差s;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
解析: (1)由(70+76+72+70+72+x6)=75,
得x6=90.
s=
=7.
(2)从前5位同学中,随机地选2位同学,其成绩的所有可能的结果为(70,76),(70,72),(70,70),(70,72),(76,72),(76,70),(76,72),(72,70),(72,72),(70,72),共10种.其中恰有1位同学成绩在区间(68,75)中的结果为(70,76),(76,72),(76,70),(76,72),共4种.故恰有1位同学成绩在区间(68,75)中的概率为P==.
20.(本小题满分12分)根据空气质量AP(为整数)的不同,可将空气质量分级如下表:
API 0~50 51~100 101~150 151~200 201~250 251~300 >300
级别 Ⅰ Ⅱ Ⅲ1 Ⅲ2 Ⅳ1 Ⅳ2 Ⅴ
状况 优 良 轻微污染 轻度污染 中度污染 中度重污染 重度污染
对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间[0,50],(50,100],(100,150],(150,200],(200,250],(250,300]进行分组,得到频率分布直方图如下图.
(1)求直方图中x的值;
(2)计算一年中空气质量分别为良和轻微污染的天数;
(3)求该城市某一周的空气质量为良或轻微污染的概率.
(结果用分数表示.已知57=78 125,27=128,
++++=,365=73×5)
解析: (1)根据频率分布直方图可知,
X=÷50
=.
(2)空气质量为Y的天数=(Y对应的频率÷组距)×组距×365天,
所以一年中空气质量为良和轻微污染的天数分别是
×50×365=119(天)和×50×365=100(天).
(3)设A、B分别表示随机事件“空气质量为良”和“空气质量为轻微污染”,则事件A与B互斥.
所以空气质量为良或轻微污染的概率是
P=P(A∪B)=P(A)+P(B)=+=.
21.(本小题满分12分)如右图所示,OA=1,在以O为圆心,OA为半径的半圆弧上任取一点B,求使△AOB的面积大于等于的概率.
解析: 如右图所示,作OC⊥OA,C在半圆弧上,过OC中点D作OA的平行线交半圆弧于E、F,所以在上取一点B,则S△AOB≥.
连接OE,OF,
因为OD=OC=OF,OC⊥EF,
所以∠DOF=60°,所以∠EOF=120°,
所以l=π·1=π.
所以P===.
22.(本小题满分14分)将一颗骰子(它的六个面分别标有点数1,2,3,4,5,6)先后抛掷两次,观察向上的点数,求:
(1)两数之积是6的倍数的概率;
(2)设第一次,第二次抛掷向上的点数分别为x、y,则logx2y=1的概率是多少;
(3)以第一次向上的点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在直线x-y=3的下方区域的概率.
解析: (1)此问题中含有36个等可能基本事件,记“向上的两数之积是6的倍数”为事件A,则由图(1)可知,事件A中含有其中的15个等可能基本事件,所以P(A)==,
即两数之积是6的倍数的概率为.
(2)此问题中含有36个等可能基本事件,记“第一次、第二次抛掷向上的点数分别为x、y,logx2y=1”为事件B,则满足logx2y=1的x、y有(2,1),(4,2),(6,3)三种情况,所以P(B)==,即第一次、第二次抛掷向上的点数分别为x、y满足logx2y=1的概率是.
(3)此问题中含有有36个等可能基本事件,记“点(x,y)在直线x-y=3的下方区域”为事件C,则由图(2)可知,事件C中含有其中的3个等可能基本事件,所以P(C)==,即点(x,y)在直线x-y=3的下方区域的概率为.
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
(本栏目内容,在学生用书中以活页形式分册装订!)
(时间120分钟,满分150分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.用“更相减损术”求225与135的最大公约数为( )
A.45 B.5
C.9 D.15
解析: 225-135=90,135-90=45,90-45=45,所以选A.
答案: A
2.某社区有500个家庭,其中高收入家庭125户,中等收入家庭280户,低收入家庭95户,为了调查社会购买力的某项指标,要从中抽取一个容量为100户的样本,记作①.某学校高一年级有12名女排运动员,要从中选出3人调查学习负担情况,记作②.那么完成上述两项调查应采用的抽样方法是( )
A.①用随机抽样法,②用系统抽样法
B.①用分层抽样法,②用随机抽样法
C.①用系统抽样法,②用分层抽样法
D.①用分层抽样法,②用系统抽样法
解析: ①中具有明显的分层,适合用分层抽样法,②中总体容量,样本容量都较小,适合用随机抽样法.故选B.
答案: B
3.在一次随机试验中,彼此互斥的事件A、B、C、D的概率分别是0.2、0.2、0.3、0.3,则下列说法正确的是( )
A.A+B与C是互斥事件,也是对立事件
B.B+C与D是互斥事件,也是对立事件
C.A+C与B+D是互斥事件,但不是对立事件
D.A与B+C+D是互斥事件,也是对立事件
解析: ∵A、B、C、D是互斥事件.
且P(A+B+C+D)=1
∴A与B+C+D是互斥事件,也是对立事件.
答案: D
4.在佛山市禅城区和南海区打的士收费办法如下:不超过2千米收7元,超过2千米的里程每千米收2.6元,另每车次超过2千米收燃油附加费1元(其他因素不考虑).相应收费系统的程序框图如图所示,则①处应填( )
A.y=7+2.6x B.y=8+2.6x
C.y=7+2.6(x-2) D.y=8+2.6(x-2)
解析: 当x>2时,按y=8+2.6(x-2)收费;
当x≤2时,收费7元.
答案: D
5.为了解某县甲、乙、丙三所学校高三数学模拟的考试成绩,采取分层抽样方法,从甲校的1 260份试卷、乙校的720份试卷、丙校的900份试卷中进行抽样调研.如果从丙校的900份试卷中抽取了45份试卷,那么这次调研共抽查的试卷份数为( )
A.88 B.99
C.144 D.63
解析: 从丙校的900份试卷中抽取了45份试卷,说明抽样比是=,所以这次调研共抽查的试卷份数为
(1 260+720+900)×=144.
答案: C
6.观察新生婴儿的体重,其频率分布直方图如下图所示,则新生婴儿体重在[2 700,3 000)的频率为( )
A.0.3 B.0.001
C.0.2 D.0.1
解析: 0.001×300=0.3,故选A.
答案: A
7.把二进制(1 101)2化为五进制数的结果是( )
A.(32)5 B.(30)5
C.(23)5 D.(31)5
解析: (1 101)2=1×23+1×22+0×21+1×20=13
∴13=(23)5.故选C.
答案: C
8.给出①②③三个程序框图如下图,下列说法正确的是( )
A.②为条件结构,③为循环结构
B.①为顺序结构,②为循环结构,③为条件结构
C.①输出的结果为35
D.③输出的a表示比66小的15的倍数中的最大数
解析: 因为②为条件结构,③为循环结构,故B不对;
①输出的数为×23.5+32=74.3;③输出的一系列数分别为15×1,15×2,…,15×66,排成一个数列,所以C、D不对.
答案: A
9.ABCD为长方形,AB=2,BC=1,O为AB的中点,在长方形ABCD内随机取一点,取到的点到O的距离大于1的概率为( )
A. B.1-
C. D.1-
解析: 如图所示,到点O的距离大于1的点应在阴影区域内,所求概率为1-=1-.
答案: B
10.右图是求样本x1,x2,…,x10平均数的程序框图,图中空白框中应填入的内容为( )
A.S=S+xn B.S=S+
C.S=S+n D.S=S+
解析: 赋值框内应为一累加求和,累和应为前面的累和再加上第n项,故选A.
答案: A
11.已知一个样本为x,1,y,5,其中x,y是方程组的解,则这个样本的标准差是( )
A.2 B.
C.5 D.
解析: 先解方程组得
当时,这个样本为-1,1,3,5.
先求其平均数:=×(-1+1+3+5)=2.
再根据样本标准差的公式,求标准差:
s=
=
==.
当时,同理可得标准差为,因此应选D.
答案: D
12.设集合A={1,2},B={1,2,3},分别从集合A和B中随机取一个数a和b,确定平面上的一个点P(a,b),记“点P(a,b)落在直线x+y=n上”为事件Cn(2≤n≤5,n∈N),且事件Cn的概率最大,则n的所有可能值为( )
A.3 B.4
C.3和4 D.2和5
解析: 点P的所有可能值为(1,1),(1,2),(1,3),(2,1),(2,2),(2,3).点P(a,b)落在直线x+y=n上(2≤n≤5,n∈N),且事件Cn的概率最大.当n=3时,P点可能是(1,2),(2,1),当n=4时,P点可能是(1,3),(2,2),即事件C3、C4的概率最大,故选D.
答案: D
二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中的横线上)
13.假设要抽查某种品牌的850颗种子的发牙率,抽取60粒进行实验,利用随机数表抽取种子时,先将850颗种子按001,002,…,850进行编号,如果从随机数表第9行第8列的数4开始向右读,请你依次写出最先检测的4颗种子的编号分别是429,786,________,078.(在横线上填上所缺的种子编号)
(下面摘取了随机数表第7行至第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74
47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50
71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07
44 38 15 51 00 13 42 99 66 02 79 54
解析: 根据随机数表法的读数规则可知4颗种子的编号应为429,786,456,078.
答案: 456
14.将一个总数为A、B、C三层,其个体数之比为5∶3∶2.若用分层抽样方法抽取容量为100的样本,则应从C中抽取________个个体.
解析: C层占总体的=,所以容量为100的样本中,C层所占个体有100×=20(个).
答案: 20
15.(2011·江西高考)如图所示是某算法的程序框图,则程序运行后输出的结果是________.
解析: 第一次进入判断框前n=1,s=0+(-1)1+1=0;
第二次进入判断框前n=2,s=0+(-1)2+2=3;
第三次进入判断框前n=3,s=3+(-1)3+3=5;
第四次进入判断框前n=4,s=5+(-1)4+4=10.
答案: 10
16.某化工厂为预测某产品的回收率y,需要研究它和原料有效成分含量x之间的相关关系.现取了8对观察值,计算得i=52,i=228,=478,iyi=1 849,则y关于x的回归方程是________.
解析: 由=及=- ,各=11.47+2.62x.
答案: =11.47+2.62x
三、解答题(本大题共6小题,共74分.解答时应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分12分)如图是为解决某个问题而绘制的程序框图,仔细分析各图框内的内容及图框之间的关系,回答下面的问题:
(1)图框②中y1=ax+b的含义是什么?
(2)该程序框图解决的是怎样的一个问题?
(3)若最终输出的结果是y1=3,y2=-2.当x取5时输出的结果 5a+b的值应该是多大?
(4)在(3)的前提下,输入的x值越大,输出的ax+b是不是越大?为什么?
解析: (1)图框②中y1=ax+b的含义:该图框在执行①的前提下,即当x=2时计算ax+b的值,并把这个值赋给y1.
(2)该程序框图解决的是求函数f(x)=ax+b的函数值的问题.其中输入的是自变量x的值,输出的是x对应的函数值.
(3)y1=3,即2a+b=3.③
y2=-2,即-3a+b=-2.④
由③④,得a=1,b=1.
∴f(x)=x+1.
∴当x取5时,f(5)=5a+b=5×1+1=6.
(4)输入的x值越大,输出的函数值ax+b越大,因为f(x)=x+1在R上是增函数.
18.(本小题满分12分)已知集合A={-9,-7,-5,-3,-1,0,2,4,6,8},在平面直角坐标系中,点(x,y)的坐标x∈A,y∈A,x≠y,求:
(1)点(x,y)不在x轴上的概率;
(2)点(x,y)正好在第二象限的概率.
解析: 点(x,y)中,x∈A,y∈A,且x≠y,共能组成90个点.
(1)B为“点不在x轴上”,即y≠0,去掉9个点,还余81个点,所以P(B)==.
(2)C为“点在第二象限”,即x<0,y>0,共有20个点,
所以P(C)==.
19.在某次测验中,有6位同学的平均成绩为75分,用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
编号n 1 2 3 4 5
成绩xn 70 76 72 70 72
(1)求第6位同学的成绩x6,及这6位同学成绩的标准差s;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
解析: (1)由(70+76+72+70+72+x6)=75,
得x6=90.
s=
=7.
(2)从前5位同学中,随机地选2位同学,其成绩的所有可能的结果为(70,76),(70,72),(70,70),(70,72),(76,72),(76,70),(76,72),(72,70),(72,72),(70,72),共10种.其中恰有1位同学成绩在区间(68,75)中的结果为(70,76),(76,72),(76,70),(76,72),共4种.故恰有1位同学成绩在区间(68,75)中的概率为P==.
20.(本小题满分12分)根据空气质量AP(为整数)的不同,可将空气质量分级如下表:
API 0~50 51~100 101~150 151~200 201~250 251~300 >300
级别 Ⅰ Ⅱ Ⅲ1 Ⅲ2 Ⅳ1 Ⅳ2 Ⅴ
状况 优 良 轻微污染 轻度污染 中度污染 中度重污染 重度污染
对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间[0,50],(50,100],(100,150],(150,200],(200,250],(250,300]进行分组,得到频率分布直方图如下图.
(1)求直方图中x的值;
(2)计算一年中空气质量分别为良和轻微污染的天数;
(3)求该城市某一周的空气质量为良或轻微污染的概率.
(结果用分数表示.已知57=78 125,27=128,
++++=,365=73×5)
解析: (1)根据频率分布直方图可知,
X=÷50
=.
(2)空气质量为Y的天数=(Y对应的频率÷组距)×组距×365天,
所以一年中空气质量为良和轻微污染的天数分别是
×50×365=119(天)和×50×365=100(天).
(3)设A、B分别表示随机事件“空气质量为良”和“空气质量为轻微污染”,则事件A与B互斥.
所以空气质量为良或轻微污染的概率是
P=P(A∪B)=P(A)+P(B)=+=.
21.(本小题满分12分)如右图所示,OA=1,在以O为圆心,OA为半径的半圆弧上任取一点B,求使△AOB的面积大于等于的概率.
解析: 如右图所示,作OC⊥OA,C在半圆弧上,过OC中点D作OA的平行线交半圆弧于E、F,所以在上取一点B,则S△AOB≥.
连接OE,OF,
因为OD=OC=OF,OC⊥EF,
所以∠DOF=60°,所以∠EOF=120°,
所以l=π·1=π.
所以P===.
22.(本小题满分14分)将一颗骰子(它的六个面分别标有点数1,2,3,4,5,6)先后抛掷两次,观察向上的点数,求:
(1)两数之积是6的倍数的概率;
(2)设第一次,第二次抛掷向上的点数分别为x、y,则logx2y=1的概率是多少;
(3)以第一次向上的点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在直线x-y=3的下方区域的概率.
解析: (1)此问题中含有36个等可能基本事件,记“向上的两数之积是6的倍数”为事件A,则由图(1)可知,事件A中含有其中的15个等可能基本事件,所以P(A)==,
即两数之积是6的倍数的概率为.
(2)此问题中含有36个等可能基本事件,记“第一次、第二次抛掷向上的点数分别为x、y,logx2y=1”为事件B,则满足logx2y=1的x、y有(2,1),(4,2),(6,3)三种情况,所以P(B)==,即第一次、第二次抛掷向上的点数分别为x、y满足logx2y=1的概率是.
(3)此问题中含有有36个等可能基本事件,记“点(x,y)在直线x-y=3的下方区域”为事件C,则由图(2)可知,事件C中含有其中的3个等可能基本事件,所以P(C)==,即点(x,y)在直线x-y=3的下方区域的概率为.
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
