【人教九上数学学霸听课笔记】22.1.1 二次函数 课件(共25张PPT)
文档属性
| 名称 | 【人教九上数学学霸听课笔记】22.1.1 二次函数 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 06:37:53 | ||
图片预览








文档简介
(共25张PPT)
22.1 二次函数的图象和性质
第二十二章
二次函数
22.1.1 二次函数
预学浅梳理
探究与应用
随堂小检测
第二十二章 二次函数
一般地,形如_______________(a,b,c是常数,a≠0)的函数,叫做
二次函数.其中,x是自变量,a,b,c分别是函数解析式的
____________、____________和__________.
y=ax2+bx+c
二次项系数
一次项系数
常数项
目标一 理解二次函数的概念
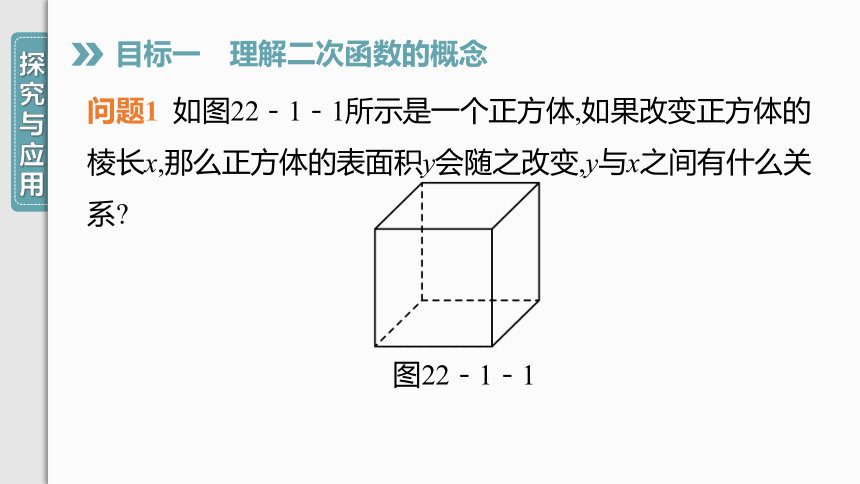
问题1
如图22-1-1所示是一个正方体,如果改变正方体的棱长x,那么正方体的表面积y会随之改变,y与x之间有什么关系?
图22-1-1
探究
正方体的六个面是全等的正方形,正方体的棱长为x,表面积为y,显然,对于x的每一个值,y都有一个对应值,即____是____的函数,y与x的具体关系可以表示为________.
y
x
y=6x2
问题2
n个球队参加比赛,每两队之间进行一场比赛,比赛的场次数m与球队数n有什么关系?
探究
每个队要与其他________个球队各比赛一场,甲队对乙队的比赛与乙队对甲队的比赛是同一场比赛,所以比赛的场次数m=_________,即m=__________,其中____是____的函数,______是自变量.
(n-1)
m
n
n
问题3
某种产品现在的年产量是20
t,计划今后两年增加产量,如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
探究
这种产品的原产量是______,一年后的产量是
__________,再经过一年后的产量是_______________,即两年后的产量y与x之间的关系可以表示为_____________,即__________________,其中______是____的函数,____是自变量.
20t
20(1+x)t
20(1+x)(1+x)t
y=20(1+x)2
y=20x2+40x+20
y
x
x
思考
观察问题1~3中所得到的函数解析式,它们有什么共同点?
解:函数都是用自变量的二次式表示的.
定义
一般地,形如y=ax2+bx+c(a,b,c是常数,________≠0)
的函数,叫做二次函数.其中x是自变量,a,b,c分别是函数解析
式的____________、____________和常数项.
a
二次项系数
一次项系数
判别二次函数的三个条件
(1)含有自变量的代数式是整式;
(2)化简后自变量的最高次数是2;
(3)二次项系数不为0.
归纳总结
例2
已知函数y=(1+m)xm2+1是关于x的二次函数,求m的值.
解:∵y=(1+m)xm2+1是关于x的二次函数,
∴m2+1=2,解得m=±1.
∵1+m≠0,∴m≠-1,∴m=1.
目标二 会根据实际问题列出二次函数的解析式
例3
如图22-1-2,用20米长的篱笆围成一个一边靠墙的矩形花圃(墙足够长),设垂直于墙的一边长为x米,矩形花圃的面积为y平方米.
(1)写出y关于x的函数解析式;
(2)当x=3时,矩形花圃的面积为多少?
图22-1-1
解:(1)y=x(20-2x)=-2x2+20x(0(2)当x=3时,y=-2×32+20×3=42,
即当x=3时,矩形花圃的面积为42平方米.
D
2.一台机器原价60万元,如果每年的折旧率为x,两年后这台机器的价格为y万元,那么y与x之间的函数解析式为( )
A.y=60(1-x)2
B.y=60(1-x)
C.y=60-x2
D.y=60(1+x)2
A
3.若函数y=(m-2)xm2-2+2x-7是关于x的二次函数,则m的取值范围是( )
A.m=±2
B.m≠2
C.m=-2
D.m为全体实数
C
4.解:(1)(2)(3)是二次函数,(4)(5)不是二次函数.
y=1-3x2,二次项系数是-3,一次项系数是0,常数项是1.
y=3x2+2x,二次项系数是3,一次项系数是2,常数项是0.
y=x(x-5)+2整理为一般形式是y=x2-5x+2,二次项系数是1,一次项系数是-5,常数项是2.
https://www.21cnjy.com/help/help_extract.php
22.1 二次函数的图象和性质
第二十二章
二次函数
22.1.1 二次函数
预学浅梳理
探究与应用
随堂小检测
第二十二章 二次函数
一般地,形如_______________(a,b,c是常数,a≠0)的函数,叫做
二次函数.其中,x是自变量,a,b,c分别是函数解析式的
____________、____________和__________.
y=ax2+bx+c
二次项系数
一次项系数
常数项
目标一 理解二次函数的概念
问题1
如图22-1-1所示是一个正方体,如果改变正方体的棱长x,那么正方体的表面积y会随之改变,y与x之间有什么关系?
图22-1-1
探究
正方体的六个面是全等的正方形,正方体的棱长为x,表面积为y,显然,对于x的每一个值,y都有一个对应值,即____是____的函数,y与x的具体关系可以表示为________.
y
x
y=6x2
问题2
n个球队参加比赛,每两队之间进行一场比赛,比赛的场次数m与球队数n有什么关系?
探究
每个队要与其他________个球队各比赛一场,甲队对乙队的比赛与乙队对甲队的比赛是同一场比赛,所以比赛的场次数m=_________,即m=__________,其中____是____的函数,______是自变量.
(n-1)
m
n
n
问题3
某种产品现在的年产量是20
t,计划今后两年增加产量,如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
探究
这种产品的原产量是______,一年后的产量是
__________,再经过一年后的产量是_______________,即两年后的产量y与x之间的关系可以表示为_____________,即__________________,其中______是____的函数,____是自变量.
20t
20(1+x)t
20(1+x)(1+x)t
y=20(1+x)2
y=20x2+40x+20
y
x
x
思考
观察问题1~3中所得到的函数解析式,它们有什么共同点?
解:函数都是用自变量的二次式表示的.
定义
一般地,形如y=ax2+bx+c(a,b,c是常数,________≠0)
的函数,叫做二次函数.其中x是自变量,a,b,c分别是函数解析
式的____________、____________和常数项.
a
二次项系数
一次项系数
判别二次函数的三个条件
(1)含有自变量的代数式是整式;
(2)化简后自变量的最高次数是2;
(3)二次项系数不为0.
归纳总结
例2
已知函数y=(1+m)xm2+1是关于x的二次函数,求m的值.
解:∵y=(1+m)xm2+1是关于x的二次函数,
∴m2+1=2,解得m=±1.
∵1+m≠0,∴m≠-1,∴m=1.
目标二 会根据实际问题列出二次函数的解析式
例3
如图22-1-2,用20米长的篱笆围成一个一边靠墙的矩形花圃(墙足够长),设垂直于墙的一边长为x米,矩形花圃的面积为y平方米.
(1)写出y关于x的函数解析式;
(2)当x=3时,矩形花圃的面积为多少?
图22-1-1
解:(1)y=x(20-2x)=-2x2+20x(0
即当x=3时,矩形花圃的面积为42平方米.
D
2.一台机器原价60万元,如果每年的折旧率为x,两年后这台机器的价格为y万元,那么y与x之间的函数解析式为( )
A.y=60(1-x)2
B.y=60(1-x)
C.y=60-x2
D.y=60(1+x)2
A
3.若函数y=(m-2)xm2-2+2x-7是关于x的二次函数,则m的取值范围是( )
A.m=±2
B.m≠2
C.m=-2
D.m为全体实数
C
4.解:(1)(2)(3)是二次函数,(4)(5)不是二次函数.
y=1-3x2,二次项系数是-3,一次项系数是0,常数项是1.
y=3x2+2x,二次项系数是3,一次项系数是2,常数项是0.
y=x(x-5)+2整理为一般形式是y=x2-5x+2,二次项系数是1,一次项系数是-5,常数项是2.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
