【人教九上数学学霸听课笔记】22.1.2 二次函数y=ax2的图象和性质 课件(共33张PPT)
文档属性
| 名称 | 【人教九上数学学霸听课笔记】22.1.2 二次函数y=ax2的图象和性质 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 06:39:14 | ||
图片预览







文档简介
(共33张PPT)
22.1 二次函数的图象和性质
第二十二章
二次函数
22.1.2 二次函数y=ax2的图象和性质
预学浅梳理
探究与应用
随堂小检测
第二十二章 二次函数
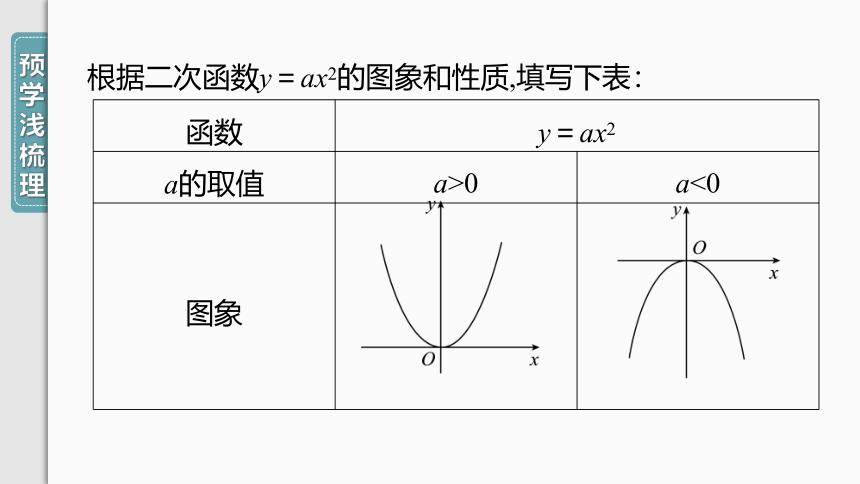
根据二次函数y=ax2的图象和性质,填写下表:
函数
y=ax2
a的取值
a>0
a<0
图象
函数
y=ax2
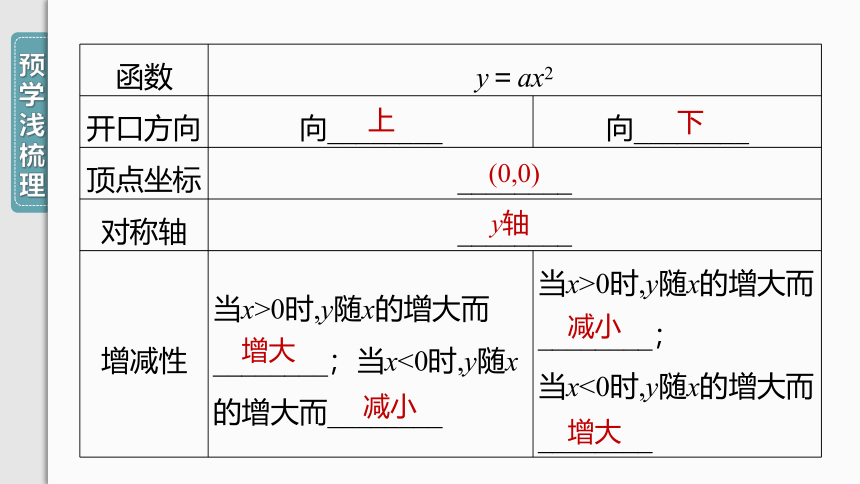
开口方向
向________
向________
顶点坐标
________
对称轴
________
增减性
当x>0时,y随x的增大而________;当x<0时,y随x的增大而________
当x>0时,y随x的增大而________;
当x<0时,y随x的增大而________
上
下
(0,0)
y轴
增大
减小
减小
增大
函数
y=ax2
最值
当x=0时,y最小值=________
当x=0时,y最大值=________
0
0
目标一 会用描点法画出二次函数y=ax2的图象,了解抛
物线的有关概念
探究
(1)画图:请根据下面的步骤用描点法画出二次函数y=x2的图象.
①列表:选取适当的x值,并计算相应的y值,完成下表:
x
…
-3
-2
-1
0
1
2
3
…
y=x2
…
…
②描点:根据上表中x,y的数值在如图22-1-3所示的平面直角坐标系中描点.
③连线:用平滑曲线顺次连接图中描出的各点.
图22-1-3
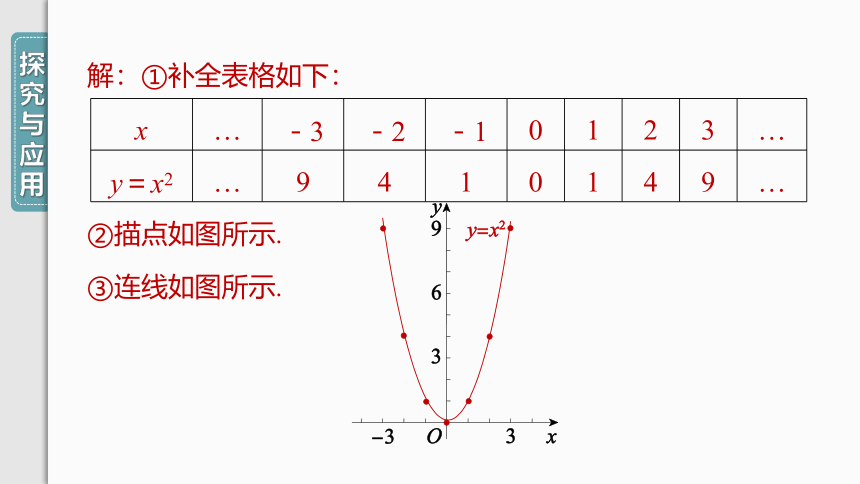
解:①补全表格如下:
②描点如图所示.
③连线如图所示.
x
…
-3
-2
-1
0
1
2
3
…
y=x2
…
9
4
1
0
1
4
9
…
(2)观察y=x2的图象并回答问题:
①二次函数y=x2的图象是一条曲线,这条曲线叫做________,抛物线y=x2关于________对称.它与对称轴的交点是________,该交点叫做抛物线y=x2的________,它是抛物线上的最________点.
抛物线
y轴
(0,0)
顶点
低
②在对称轴________,抛物线y=x2从左到右下降;在对称轴右侧,抛物线从左到右________.也就是说,当x<0时,y随x的增大而________;当x>0时,y随x的增大而________.
左侧
上升
减小
增大
目标二 探究二次函数y=ax2的图象与性质
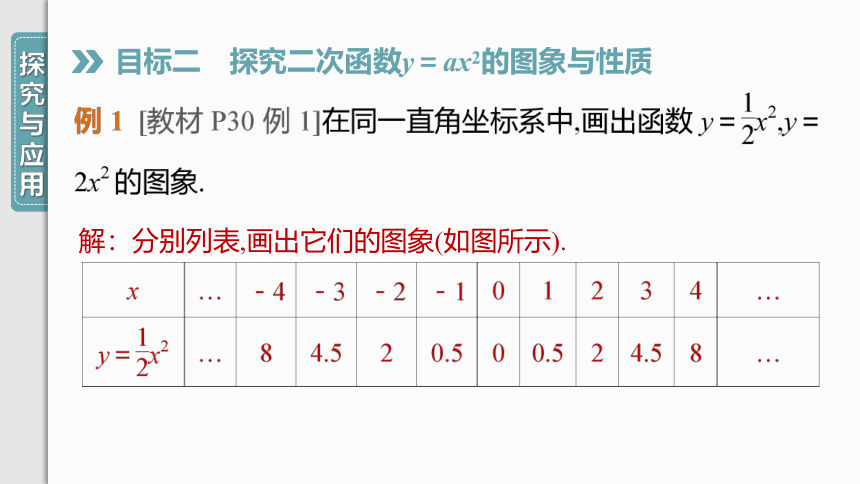
解:分别列表,画出它们的图象(如图所示).
x
…
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
…
y=2x2
…
8
4.5
2
0.5
0
0.5
2
4.5
8
…
解:(1)共同点:函数图象的开口向上,对称轴是y轴,顶点是原点,顶点是抛物线的最低点.
不同点:开口大小不同.
(2)当a>0时,二次函数y=ax2的图象开口向上,对称轴是y轴,顶点是原点,顶点是抛物线的最低点,a越大,抛物线的开口越小.
解:(1)如图所示:
共同点:函数图象的开口向下,对称轴是y轴,顶点是原点,顶点是抛物线的最高点.
不同点:开口大小不同.
(2)当a<0时,二次函数y=ax2的图象开口向下,对称轴是y轴,顶点是原点,顶点是抛物线的最高点,a越小,抛物线的开口越小.
归纳
二次函数y=ax2的图象特征与性质
1.一般地,抛物线y=ax2的对称轴是________轴,顶点是
________.
y
原点
归纳
2.如果a>0,
(1)抛物线的开口向________,顶点是抛物线的最______点;
(2)当x<0时,y随x的增大而________,当x>0时,y随x的增大而
________.
上
低
减小
增大
归纳
3.如果a<0,
(1)抛物线的开口向________,顶点是抛物线的最______点;
(2)当x<0时,y随x的增大而________,当x>0时,y随x的增大而
________.
4.对于抛物线y=ax2,|a|越大,抛物线的开口越________.
下
高
增大
减小
小
解:(1)抛物线y=5x2的开口向上,对称轴是y轴,顶点是原点.
(2)抛物线y=-4x2的开口向下,对称轴是y轴,顶点是原点.
目标三 能应用二次函数y=ax2的图象和性质解决简单的
问题
例2
二次函数y=(2m+1)x2的图象如图22-1-4所示.
(1)m的取值范围是________;
(2)若在抛物线上有两个点A(2,y1),B(5,y2),
则y1________y2.
图22-1-4
<
变式
已知y=(k+2)xk2+k-4是关于x的二次函数,且当x>0时,y随x的增大而增大,则k=________.
2
变式
若二次函数y=(2-m)x|m|-3的图象开口向下,求m的值.
解:∵y=(2-m)x|m|-3是二次函数,
∴|m|-3=2,解得m=5或m=-5.
上述解题过程正确吗?如果不正确,请写出正确的解题过程.
解:上述解题过程不正确.
正确的解题过程如下:
∵y=(2-m)x|m|-3是二次函数,
∴|m|-3=2,解得m=5或m=-5.
∵二次函数y=(2-m)x|m|-3的图象开口向下,
∴2-m<0,解得m>2,故m=5
1.对于函数y=x2,下列判断中,正确的是( )
A.若m,n互为相反数,则x=m与x=n对应的函数值相等
B.对于同一自变量x,有两个函数值与之对应
C.对于任意一个实数y,有两个x值与之对应
D.对于任意一个实数x,都有y>0
A
2.当k________时,抛物线y=(1-k)x2的开口向上.此时,当x<0时,y随x的增大而________;当x>0时,y随x的增大而______.
<1
减小
增大
3.在如图22-1-5所示的坐标系中画出二次函数y=-8x2的图象,并解决下列问题:
解:二次函数y=-8x2的图象如图所示.
图22-1-5
(1)抛物线的对称轴是________,顶点坐标是________.
(2)抛物线的开口向________.
(3)抛物线在对称轴左边的部分,函数
值随自变量取值的增大而________;
在对称轴右边的部分,函数值随自变
量取值的增大而________.
y轴
(0,0)
下
增大
减小
https://www.21cnjy.com/help/help_extract.php
22.1 二次函数的图象和性质
第二十二章
二次函数
22.1.2 二次函数y=ax2的图象和性质
预学浅梳理
探究与应用
随堂小检测
第二十二章 二次函数
根据二次函数y=ax2的图象和性质,填写下表:
函数
y=ax2
a的取值
a>0
a<0
图象
函数
y=ax2
开口方向
向________
向________
顶点坐标
________
对称轴
________
增减性
当x>0时,y随x的增大而________;当x<0时,y随x的增大而________
当x>0时,y随x的增大而________;
当x<0时,y随x的增大而________
上
下
(0,0)
y轴
增大
减小
减小
增大
函数
y=ax2
最值
当x=0时,y最小值=________
当x=0时,y最大值=________
0
0
目标一 会用描点法画出二次函数y=ax2的图象,了解抛
物线的有关概念
探究
(1)画图:请根据下面的步骤用描点法画出二次函数y=x2的图象.
①列表:选取适当的x值,并计算相应的y值,完成下表:
x
…
-3
-2
-1
0
1
2
3
…
y=x2
…
…
②描点:根据上表中x,y的数值在如图22-1-3所示的平面直角坐标系中描点.
③连线:用平滑曲线顺次连接图中描出的各点.
图22-1-3
解:①补全表格如下:
②描点如图所示.
③连线如图所示.
x
…
-3
-2
-1
0
1
2
3
…
y=x2
…
9
4
1
0
1
4
9
…
(2)观察y=x2的图象并回答问题:
①二次函数y=x2的图象是一条曲线,这条曲线叫做________,抛物线y=x2关于________对称.它与对称轴的交点是________,该交点叫做抛物线y=x2的________,它是抛物线上的最________点.
抛物线
y轴
(0,0)
顶点
低
②在对称轴________,抛物线y=x2从左到右下降;在对称轴右侧,抛物线从左到右________.也就是说,当x<0时,y随x的增大而________;当x>0时,y随x的增大而________.
左侧
上升
减小
增大
目标二 探究二次函数y=ax2的图象与性质
解:分别列表,画出它们的图象(如图所示).
x
…
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
…
y=2x2
…
8
4.5
2
0.5
0
0.5
2
4.5
8
…
解:(1)共同点:函数图象的开口向上,对称轴是y轴,顶点是原点,顶点是抛物线的最低点.
不同点:开口大小不同.
(2)当a>0时,二次函数y=ax2的图象开口向上,对称轴是y轴,顶点是原点,顶点是抛物线的最低点,a越大,抛物线的开口越小.
解:(1)如图所示:
共同点:函数图象的开口向下,对称轴是y轴,顶点是原点,顶点是抛物线的最高点.
不同点:开口大小不同.
(2)当a<0时,二次函数y=ax2的图象开口向下,对称轴是y轴,顶点是原点,顶点是抛物线的最高点,a越小,抛物线的开口越小.
归纳
二次函数y=ax2的图象特征与性质
1.一般地,抛物线y=ax2的对称轴是________轴,顶点是
________.
y
原点
归纳
2.如果a>0,
(1)抛物线的开口向________,顶点是抛物线的最______点;
(2)当x<0时,y随x的增大而________,当x>0时,y随x的增大而
________.
上
低
减小
增大
归纳
3.如果a<0,
(1)抛物线的开口向________,顶点是抛物线的最______点;
(2)当x<0时,y随x的增大而________,当x>0时,y随x的增大而
________.
4.对于抛物线y=ax2,|a|越大,抛物线的开口越________.
下
高
增大
减小
小
解:(1)抛物线y=5x2的开口向上,对称轴是y轴,顶点是原点.
(2)抛物线y=-4x2的开口向下,对称轴是y轴,顶点是原点.
目标三 能应用二次函数y=ax2的图象和性质解决简单的
问题
例2
二次函数y=(2m+1)x2的图象如图22-1-4所示.
(1)m的取值范围是________;
(2)若在抛物线上有两个点A(2,y1),B(5,y2),
则y1________y2.
图22-1-4
<
变式
已知y=(k+2)xk2+k-4是关于x的二次函数,且当x>0时,y随x的增大而增大,则k=________.
2
变式
若二次函数y=(2-m)x|m|-3的图象开口向下,求m的值.
解:∵y=(2-m)x|m|-3是二次函数,
∴|m|-3=2,解得m=5或m=-5.
上述解题过程正确吗?如果不正确,请写出正确的解题过程.
解:上述解题过程不正确.
正确的解题过程如下:
∵y=(2-m)x|m|-3是二次函数,
∴|m|-3=2,解得m=5或m=-5.
∵二次函数y=(2-m)x|m|-3的图象开口向下,
∴2-m<0,解得m>2,故m=5
1.对于函数y=x2,下列判断中,正确的是( )
A.若m,n互为相反数,则x=m与x=n对应的函数值相等
B.对于同一自变量x,有两个函数值与之对应
C.对于任意一个实数y,有两个x值与之对应
D.对于任意一个实数x,都有y>0
A
2.当k________时,抛物线y=(1-k)x2的开口向上.此时,当x<0时,y随x的增大而________;当x>0时,y随x的增大而______.
<1
减小
增大
3.在如图22-1-5所示的坐标系中画出二次函数y=-8x2的图象,并解决下列问题:
解:二次函数y=-8x2的图象如图所示.
图22-1-5
(1)抛物线的对称轴是________,顶点坐标是________.
(2)抛物线的开口向________.
(3)抛物线在对称轴左边的部分,函数
值随自变量取值的增大而________;
在对称轴右边的部分,函数值随自变
量取值的增大而________.
y轴
(0,0)
下
增大
减小
https://www.21cnjy.com/help/help_extract.php
同课章节目录
