【人教九上数学学霸听课笔记】22.1.3 第3课时 二次函数y=a(x-h)2+k的图象和性质 课件(共29张PPT)
文档属性
| 名称 | 【人教九上数学学霸听课笔记】22.1.3 第3课时 二次函数y=a(x-h)2+k的图象和性质 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 06:32:20 | ||
图片预览








文档简介
(共29张PPT)
22.1.3 二次函数y=a(x-h)2+k的图象和性质
第二十二章
二次函数
第3课时 二次函数y=a(x-h)2+k的图象和性质
预学浅梳理
探究与应用
随堂小检测
第二十二章 二次函数
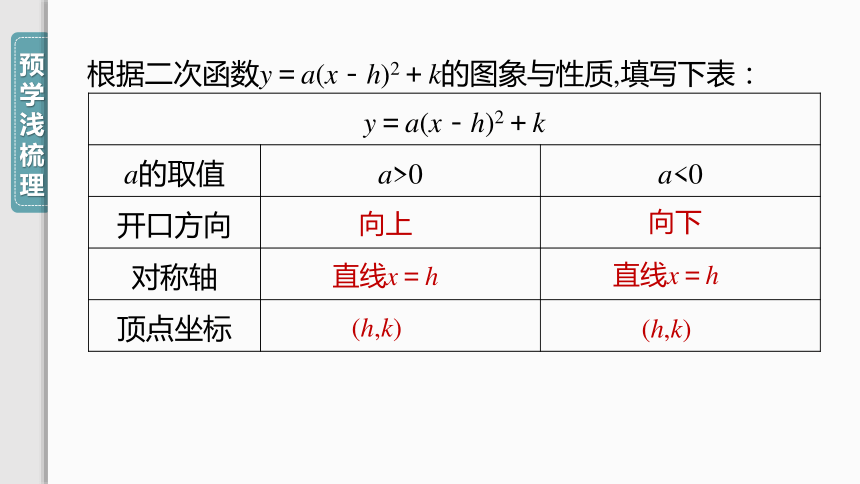
根据二次函数y=a(x-h)2+k的图象与性质,填写下表:
y=a(x-h)2+k
a的取值
a>0
a<0
开口方向
对称轴
顶点坐标
向上
向下
直线x=h
直线x=h
(h,k)
(h,k)
y=a(x-h)2+k
a的取值
a>0
a<0
增减性
当xh时,y随x的增大而________
当xh时,y随x的增大而________
最值
当x=___时,y有最小值,y最小值=____
当x=____时,y有最大值,y最大值=____
减小
增大
增大
减小
h
k
h
k
目标一 理解并掌握二次函数y=a(x-h)2+k的图象及性质
归纳
二次函数y=a(x-h)2+k图象的特征与性质
1.二次函数y=a(x-h)2+k的图象的对称轴是________,顶点
坐标是________.
2.当a>0时,图象开口向________,当x________,当x>h时,y随x的增大而________,当x=h时,y有最
________值是________.
直线x=h
(h,k)
上
减小
增大
小
k
归纳
3.当a<0时,图象开口向________,当x________,当x>h时,y随x的增大而________,当x=________
时,y有最大值是________.
下
增大
减小
h
k
练习
指出下列拋物线的开口方向、顶点坐标和对称轴,并说明当x取何值时,y随x的增大而增大;当x取何值时,y随x的增大而减小.
(1)y=4(x+1)2-4; (2)y=-2(x-1)2+3.
解:(1)抛物线y=4(x+1)2-4开口向上,顶点坐标为(-1,-4),对称轴为直线x=-1,当x>-1时,y随x的增大而增大,当x<-1时,y随x的增大而减小.
(2)抛物线y=-2(x-1)2+3开口向下,顶点坐标为(1,3),对称轴为直线x=1,当x<1时,y随x的增大而增大,当x>1时,y随x的增大而减小.
目标二 理解抛物线y=a(x-h)2+k与抛物线y=ax2之间
的位置关系
解:如图所示.方法一:
抛物线y=ax2与y=a(x±h)2±k(h>0,k>0)之间的位置关系
规律总结
练习
函数y=4(x+1)2-2的图象是由函数y=4x2的图象如何平移得到的?
解:将函数y=4x2的图象先向左平移1个单位长度,再向下平移2个单位长度得到函数y=4(x+1)2-2的图象.(平移方法不唯一)
目标三 能用二次函数y=a(x-h)2+k解决简单的实际问题
例3
[教材P36例4]要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1
m处达到最高,高度为3
m,水柱落地处离池中心3
m,水管应多长?
解:以水管与地面交点为原点,原点与水柱落地处所在直线为x轴,水管所在直线为y轴,建立直角坐标系,如图.
因为点(1,3)是图中这段抛物线的顶点,
所以可设这段抛物线对应的函数解析式
是y=a(x-1)2+3(0≤x≤3).
感悟
实际问题中建立合适坐标系的重要性
在用二次函数建模方法解决实际问题时,建立不同的坐标系,会得到不同的函数模型,比如例3中取水管与地面的交点为原点,和取喷水头为原点建立坐标系之后,得到的函数解析式会不同,我们可根据实际情况以计算简便为主选取合适的坐标系.
图J22-1-1
解:如图,以直线OA为x轴,过点O且与OA垂直的直线为y轴,建立平面直角坐标系,
则抛物线的顶点坐标是(4,3),
故可设抛物线的函数解析式为
y=a(x-4)2+3.
解得x1=10,x2=-2(不合题意,舍去).
故这名男生推出铅球的水平距离OA是10
m.
1.填表:
向下
y轴
(0,0)
向上
y轴
(0,5)
向下
直线x=-4
(-4,0)
向上
直线x=-2
(-2,-7)
[解析]
可将各解析式统一写成y=a(x-h)2+k的形式,再根据图象的性质填写.
y=-5x2?y=-5(x-0)2+0;
y=-3(x+4)2?y=-3[x-(-4)]2+0;
y=4(x+2)2-7?y=4[x-(-2)]2+(-7).
2.看图填空:
图22-1-10
下
4
右
5
右
5
下
4
x
…
3
4
5
6
7
8
9
…
y
…
3
…
(2)描点画图:
(3)设A(3.5,y1),B(5.5,y2),则y1________y2.
图22-1-11
解:(1)补全表格如下:
(2)如图所示.
(3)>
x
…
3
4
5
6
7
8
9
…
y
…
7.5
5
3.5
3
3.5
5
7.5
…
https://www.21cnjy.com/help/help_extract.php
22.1.3 二次函数y=a(x-h)2+k的图象和性质
第二十二章
二次函数
第3课时 二次函数y=a(x-h)2+k的图象和性质
预学浅梳理
探究与应用
随堂小检测
第二十二章 二次函数
根据二次函数y=a(x-h)2+k的图象与性质,填写下表:
y=a(x-h)2+k
a的取值
a>0
a<0
开口方向
对称轴
顶点坐标
向上
向下
直线x=h
直线x=h
(h,k)
(h,k)
y=a(x-h)2+k
a的取值
a>0
a<0
增减性
当x
当x
最值
当x=___时,y有最小值,y最小值=____
当x=____时,y有最大值,y最大值=____
减小
增大
增大
减小
h
k
h
k
目标一 理解并掌握二次函数y=a(x-h)2+k的图象及性质
归纳
二次函数y=a(x-h)2+k图象的特征与性质
1.二次函数y=a(x-h)2+k的图象的对称轴是________,顶点
坐标是________.
2.当a>0时,图象开口向________,当x
________值是________.
直线x=h
(h,k)
上
减小
增大
小
k
归纳
3.当a<0时,图象开口向________,当x
时,y有最大值是________.
下
增大
减小
h
k
练习
指出下列拋物线的开口方向、顶点坐标和对称轴,并说明当x取何值时,y随x的增大而增大;当x取何值时,y随x的增大而减小.
(1)y=4(x+1)2-4; (2)y=-2(x-1)2+3.
解:(1)抛物线y=4(x+1)2-4开口向上,顶点坐标为(-1,-4),对称轴为直线x=-1,当x>-1时,y随x的增大而增大,当x<-1时,y随x的增大而减小.
(2)抛物线y=-2(x-1)2+3开口向下,顶点坐标为(1,3),对称轴为直线x=1,当x<1时,y随x的增大而增大,当x>1时,y随x的增大而减小.
目标二 理解抛物线y=a(x-h)2+k与抛物线y=ax2之间
的位置关系
解:如图所示.方法一:
抛物线y=ax2与y=a(x±h)2±k(h>0,k>0)之间的位置关系
规律总结
练习
函数y=4(x+1)2-2的图象是由函数y=4x2的图象如何平移得到的?
解:将函数y=4x2的图象先向左平移1个单位长度,再向下平移2个单位长度得到函数y=4(x+1)2-2的图象.(平移方法不唯一)
目标三 能用二次函数y=a(x-h)2+k解决简单的实际问题
例3
[教材P36例4]要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1
m处达到最高,高度为3
m,水柱落地处离池中心3
m,水管应多长?
解:以水管与地面交点为原点,原点与水柱落地处所在直线为x轴,水管所在直线为y轴,建立直角坐标系,如图.
因为点(1,3)是图中这段抛物线的顶点,
所以可设这段抛物线对应的函数解析式
是y=a(x-1)2+3(0≤x≤3).
感悟
实际问题中建立合适坐标系的重要性
在用二次函数建模方法解决实际问题时,建立不同的坐标系,会得到不同的函数模型,比如例3中取水管与地面的交点为原点,和取喷水头为原点建立坐标系之后,得到的函数解析式会不同,我们可根据实际情况以计算简便为主选取合适的坐标系.
图J22-1-1
解:如图,以直线OA为x轴,过点O且与OA垂直的直线为y轴,建立平面直角坐标系,
则抛物线的顶点坐标是(4,3),
故可设抛物线的函数解析式为
y=a(x-4)2+3.
解得x1=10,x2=-2(不合题意,舍去).
故这名男生推出铅球的水平距离OA是10
m.
1.填表:
向下
y轴
(0,0)
向上
y轴
(0,5)
向下
直线x=-4
(-4,0)
向上
直线x=-2
(-2,-7)
[解析]
可将各解析式统一写成y=a(x-h)2+k的形式,再根据图象的性质填写.
y=-5x2?y=-5(x-0)2+0;
y=-3(x+4)2?y=-3[x-(-4)]2+0;
y=4(x+2)2-7?y=4[x-(-2)]2+(-7).
2.看图填空:
图22-1-10
下
4
右
5
右
5
下
4
x
…
3
4
5
6
7
8
9
…
y
…
3
…
(2)描点画图:
(3)设A(3.5,y1),B(5.5,y2),则y1________y2.
图22-1-11
解:(1)补全表格如下:
(2)如图所示.
(3)>
x
…
3
4
5
6
7
8
9
…
y
…
7.5
5
3.5
3
3.5
5
7.5
…
https://www.21cnjy.com/help/help_extract.php
同课章节目录
