【人教九上数学学霸听课笔记】22.3 第3课时 二次函数与拱桥类问题 课件(共27张PPT)
文档属性
| 名称 | 【人教九上数学学霸听课笔记】22.3 第3课时 二次函数与拱桥类问题 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 06:43:50 | ||
图片预览







文档简介
(共27张PPT)
22.3 实际问题与二次函数
第二十二章
二次函数
第3课时 二次函数与拱桥类问题
探究与应用
随堂小检测
第二十二章 二次函数
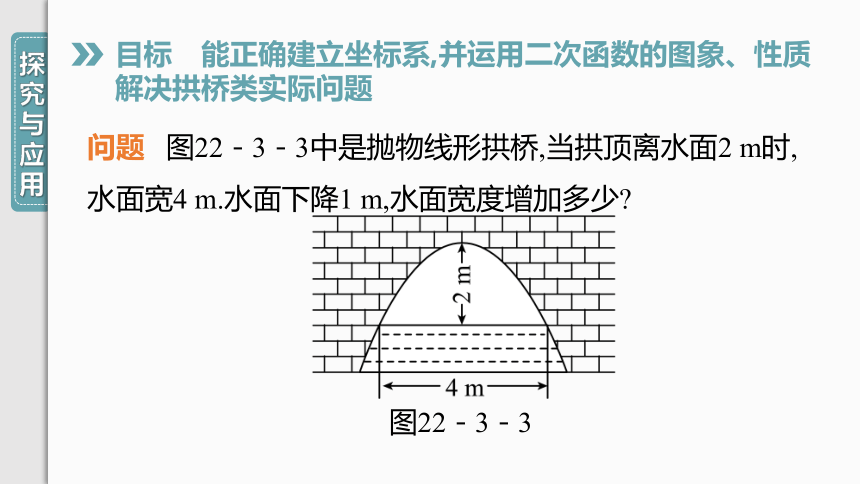
目标 能正确建立坐标系,并运用二次函数的图象、性质
解决拱桥类实际问题
问题
图22-3-3中是抛物线形拱桥,当拱顶离水面2
m时,水面宽4
m.水面下降1
m,水面宽度增加多少?
图22-3-3
分析
(1)什么函数的图象是抛物线?此拱挢问题可利用什么函数来解决?
解:二次函数的图象是抛物线,此拱桥问题可利用二次函数来解决.
(2)要求出此抛物线的解析式,则需要建立直角坐标系.怎样建立直角坐标系呢?
请按下面提供的方法画图建立坐标系,求出函数解析式并解决问题.
方法一:以水面所在直线为x轴,水面的中点为原点建立直角坐标系.?
解:方法一:如图所示:
由题意,设抛物线的解析式为y=ax2+b.
∵当拱顶离水面2
m时,水面宽4
m,
∴C(0,2),B(2,0).
当水面下降1
m时,水面的纵坐标为-1.
令y=-1,
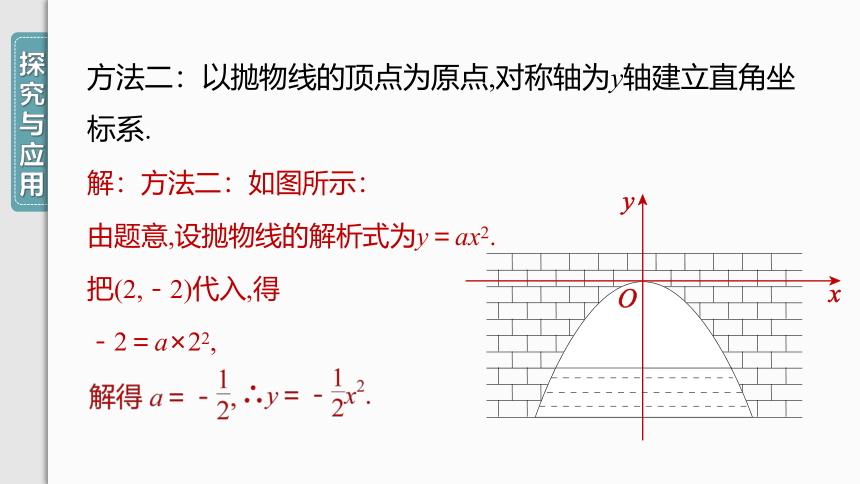
方法二:以抛物线的顶点为原点,对称轴为y轴建立直角坐标系.
解:方法二:如图所示:
由题意,设抛物线的解析式为y=ax2.
把(2,-2)代入,得
-2=a×22,
当水面下降1
m时,水面的纵坐标为-3.
方法三:以抛物线与水面的左侧交点为原点,水面所在直线为x轴建立直角坐标系.
解:方法三:如图所示:
根据题意知,抛物线与x轴的交
点为(0,0),(4,0),其顶点坐标为(2,2).
设抛物线的解析式为y=a(x-2)2+2.
将(0,0)代入,得4a+2=0,
当水面下降1
m时,水面的纵坐标为-1.
比较上面的三种方法,你觉得哪种方法更简便?
解:方法二更简便.
利用二次函数解决拱桥类问题的“五步法”
(1)恰当地建立______________;
(2)将已知条件转化为点的坐标;
(3)合理地设出所求函数的________;
(4)代入已知条件或点的坐标求出解析式;
(5)利用解析式求解问题.
归纳总结
平面直角坐标系
解析式
图22-3-4
∵点A(0,10)在抛物线上,
解得x1=-1(舍去),x2=3,∴OB=3.
即水流落地点B离墙的距离OB为3
m.
练习
如图22-3-5①为抛物线形拱桥,在正常水位下测得主拱宽24
m,最高点离水面8
m.以水平线AB为x轴,AB的中点为原点建立直角坐标系(如图②).桥边有一浮在水面部分高
4
m,最宽处为18
m的船,试探索此船在正常水位时能否开到桥下,并说明理由.
图22-3-5
解:不能.理由如下:
由题意可得B(12,0),C(0,8).
因为抛物线的顶点为C(0,8),所以可设抛物线的解析式为y=ax2+8.
所以此船在正常水位时不能开到桥下.
1.如图22-3-6,一桥拱呈抛物线状,桥的最大高度CM是
16
m,跨度AB是40
m,在线段AB上离中点M处5
m的地方,桥的高度DN是多少米?
图22-3-6
解:如图22-3-7所示,以直线AB为x轴,向右为正方向﹐点M为坐标原点,建立直角坐标系,则可设抛物线的解析式为y=ax2+
_________.
图22-3-7
16
因为抛物线经过点B(20,0),
所以0=a×202+________,解得a=________,
所以抛物线的解析式为y=_____________.
当x=5时,y=________.
答:在线段AB上离中点M处5
m的
地方,桥的高度DN是________
m.
16
15
15
2.如图22-3-8所示,某工厂的大门是一抛物线形水泥建筑物,大门的地面宽度为8
m,两侧距地面3
m的高处各有一个壁灯,两壁灯之间的水平距离为6
m,求工厂大门的高(水泥建筑物厚度忽略不计).
图22-3-8
解:如图所示,以抛物线的对称轴为y轴,向上为正方向,对称轴与地面的交点为坐标原点建立直角坐标系,则可设抛物线的解析式为y=ax2+h.
因为抛物线经过点(-4,0)和(-3,3),
https://www.21cnjy.com/help/help_extract.php
22.3 实际问题与二次函数
第二十二章
二次函数
第3课时 二次函数与拱桥类问题
探究与应用
随堂小检测
第二十二章 二次函数
目标 能正确建立坐标系,并运用二次函数的图象、性质
解决拱桥类实际问题
问题
图22-3-3中是抛物线形拱桥,当拱顶离水面2
m时,水面宽4
m.水面下降1
m,水面宽度增加多少?
图22-3-3
分析
(1)什么函数的图象是抛物线?此拱挢问题可利用什么函数来解决?
解:二次函数的图象是抛物线,此拱桥问题可利用二次函数来解决.
(2)要求出此抛物线的解析式,则需要建立直角坐标系.怎样建立直角坐标系呢?
请按下面提供的方法画图建立坐标系,求出函数解析式并解决问题.
方法一:以水面所在直线为x轴,水面的中点为原点建立直角坐标系.?
解:方法一:如图所示:
由题意,设抛物线的解析式为y=ax2+b.
∵当拱顶离水面2
m时,水面宽4
m,
∴C(0,2),B(2,0).
当水面下降1
m时,水面的纵坐标为-1.
令y=-1,
方法二:以抛物线的顶点为原点,对称轴为y轴建立直角坐标系.
解:方法二:如图所示:
由题意,设抛物线的解析式为y=ax2.
把(2,-2)代入,得
-2=a×22,
当水面下降1
m时,水面的纵坐标为-3.
方法三:以抛物线与水面的左侧交点为原点,水面所在直线为x轴建立直角坐标系.
解:方法三:如图所示:
根据题意知,抛物线与x轴的交
点为(0,0),(4,0),其顶点坐标为(2,2).
设抛物线的解析式为y=a(x-2)2+2.
将(0,0)代入,得4a+2=0,
当水面下降1
m时,水面的纵坐标为-1.
比较上面的三种方法,你觉得哪种方法更简便?
解:方法二更简便.
利用二次函数解决拱桥类问题的“五步法”
(1)恰当地建立______________;
(2)将已知条件转化为点的坐标;
(3)合理地设出所求函数的________;
(4)代入已知条件或点的坐标求出解析式;
(5)利用解析式求解问题.
归纳总结
平面直角坐标系
解析式
图22-3-4
∵点A(0,10)在抛物线上,
解得x1=-1(舍去),x2=3,∴OB=3.
即水流落地点B离墙的距离OB为3
m.
练习
如图22-3-5①为抛物线形拱桥,在正常水位下测得主拱宽24
m,最高点离水面8
m.以水平线AB为x轴,AB的中点为原点建立直角坐标系(如图②).桥边有一浮在水面部分高
4
m,最宽处为18
m的船,试探索此船在正常水位时能否开到桥下,并说明理由.
图22-3-5
解:不能.理由如下:
由题意可得B(12,0),C(0,8).
因为抛物线的顶点为C(0,8),所以可设抛物线的解析式为y=ax2+8.
所以此船在正常水位时不能开到桥下.
1.如图22-3-6,一桥拱呈抛物线状,桥的最大高度CM是
16
m,跨度AB是40
m,在线段AB上离中点M处5
m的地方,桥的高度DN是多少米?
图22-3-6
解:如图22-3-7所示,以直线AB为x轴,向右为正方向﹐点M为坐标原点,建立直角坐标系,则可设抛物线的解析式为y=ax2+
_________.
图22-3-7
16
因为抛物线经过点B(20,0),
所以0=a×202+________,解得a=________,
所以抛物线的解析式为y=_____________.
当x=5时,y=________.
答:在线段AB上离中点M处5
m的
地方,桥的高度DN是________
m.
16
15
15
2.如图22-3-8所示,某工厂的大门是一抛物线形水泥建筑物,大门的地面宽度为8
m,两侧距地面3
m的高处各有一个壁灯,两壁灯之间的水平距离为6
m,求工厂大门的高(水泥建筑物厚度忽略不计).
图22-3-8
解:如图所示,以抛物线的对称轴为y轴,向上为正方向,对称轴与地面的交点为坐标原点建立直角坐标系,则可设抛物线的解析式为y=ax2+h.
因为抛物线经过点(-4,0)和(-3,3),
https://www.21cnjy.com/help/help_extract.php
同课章节目录
