【人教九上数学学霸听课笔记】22.5 第二十二章 二次函数章末总结提升 课件(共45张PPT)
文档属性
| 名称 | 【人教九上数学学霸听课笔记】22.5 第二十二章 二次函数章末总结提升 课件(共45张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 06:47:52 | ||
图片预览









文档简介
(共45张PPT)
本章总结提升
第二十二章
二次函数
本章总结提升
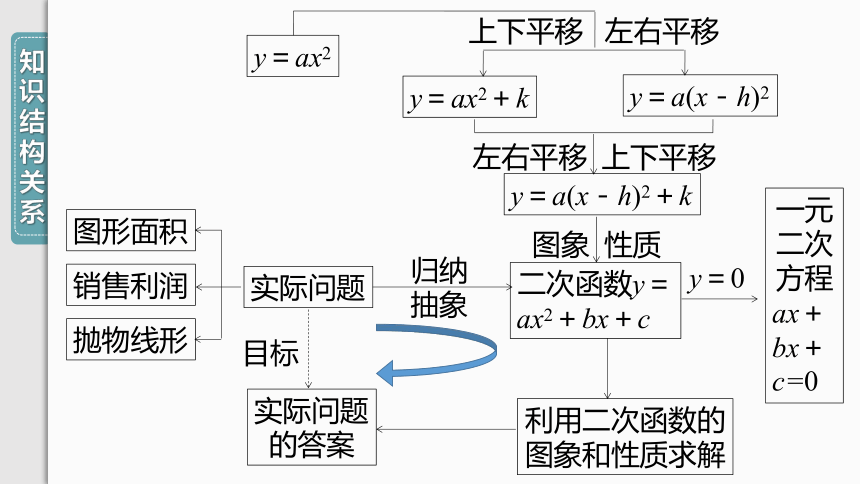
知识结构关系
重点模块总结
综合能力提升
第二十二章 二次函数
图形面积
销售利润
抛物线形
实际问题
实际问题
的答案
目标
归纳
抽象
二次函数y=
ax2+bx+c
利用二次函数的
图象和性质求解
y=0
一元二次方程
ax+
bx+c=0
图象
性质
y=a(x-h)2+k
左右平移
上下平移
y=ax2+k
y=a(x-h)2
上下平移
左右平移
y=ax2
模块1 抛物线的平移
抛物线y=ax2经过怎样的平移可以得到抛物线y=a(x-h)2+k?
例1
(1)[2020·绥化]将抛物线y=2(x-3)2+2向左平移3个单位长度,再向下平移2个单位长度,得到的抛物线的解析式是
( )
A.y=2(x-6)2
B.y=2(x-6)2+4
C.y=2x2
D.y=2x2+4
C
(2)若将抛物线y=ax2+bx+c向下平移3个单位长度,再向左平移1个单位长度得到抛物线y=2(x-1)2+3,则a=_______,
b=________,c=________.
[解析]
∵平移前后抛物线的开口方向和大小相同,∴a=2.依题意可知,平移前的抛物线的顶点坐标是(2,6),∴平移前的抛物线的解析式为y=2(x-2)2+6,即y=2x2-8x+14,∴b=-8,c=14.
2
-8
14
将抛物线y=ax2+bx+c用配方法化成y=a(x-h)2+k的形式,而任意抛物线y=a(x-h)2+k均可由抛物线y=ax2平移得到,具体平移方法如图22-T-1:
归纳总结
图22-T-1
模块2 二次函数的图象和性质
结合二次函数的图象回顾二次函数的性质,例如根据抛物线的开口方向、顶点坐标,说明二次函数在什么情况下取得最大(小)值.
例2
[2020·襄阳]二次函数y=ax2+bx+c的图象如图22-T-2所示,有下列结论:①ac<0;②3a+c=0;③4ac-b2<0;④当x>-1时,y随着x的增大而减小.其中正确的有
( )
A.4个
B.3个
C.2个
D.1个
图22-T-2
B
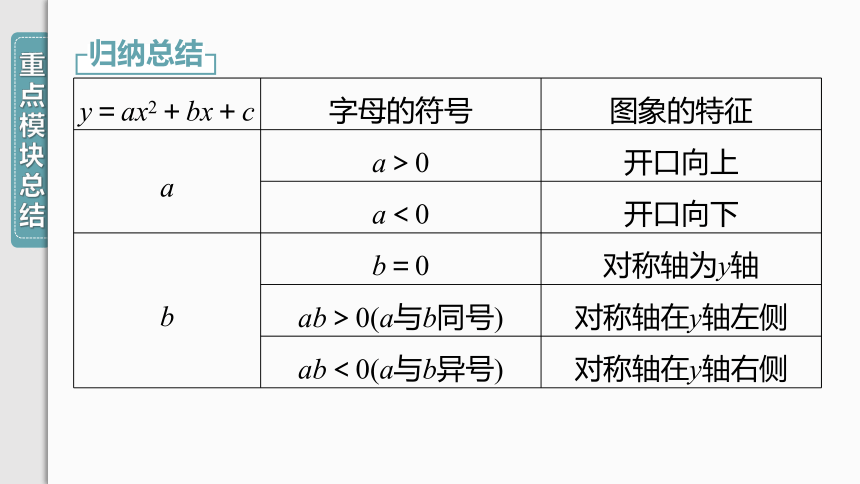
归纳总结
y=ax2+bx+c
字母的符号
图象的特征
a
a>0
开口向上
a<0
开口向下
b
b=0
对称轴为y轴
ab>0(a与b同号)
对称轴在y轴左侧
ab<0(a与b异号)
对称轴在y轴右侧
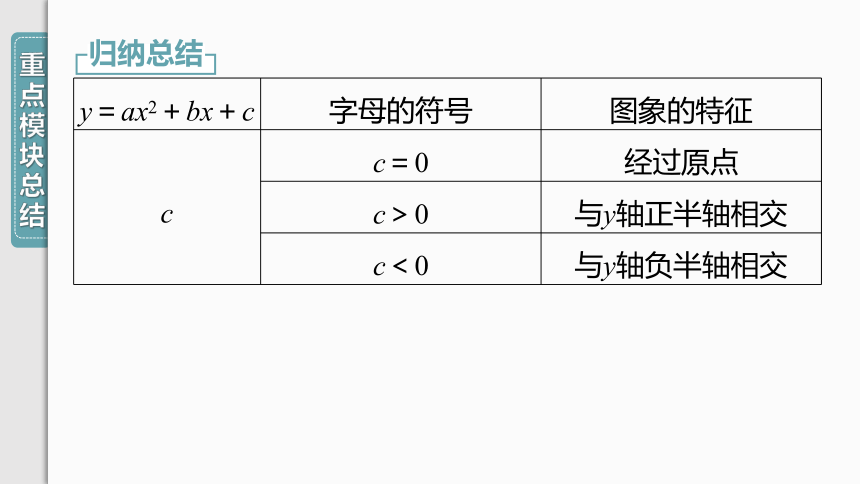
归纳总结
y=ax2+bx+c
字母的符号
图象的特征
c
c=0
经过原点
c>0
与y轴正半轴相交
c<0
与y轴负半轴相交
归纳总结
y=ax2+bx+c
字母的符号
图象的特征
b2-4ac
b2-4ac=0
与x轴有唯一公共点(顶点)
b2-4ac>0
与x轴有两个公共点
b2-4ac<0
与x轴没有公共点
归纳总结
特殊关系
当x=1时,y=a+b+c;
当x=-1时,y=a-b+c;
若a+b+c>0,则当x=1时,y>0;
若a-b+c>0,则当x=-1时,y>0
模块3 用待定系数法求二次函数的解析式
用待定系数法求二次函数的解析式的方法有哪些?
例3
已知一抛物线与x轴的交点是A(-2,0),B(1,0),且经过点C(2,8),求此抛物线的解析式.
[解析]
已知此抛物线经过三点,故可设一般式求解析式.若仔细观察点A,B的特征,又知点A,B是抛物线与x轴的交点,因此又可设交点式求解析式.
解:解法一:设此抛物线的解析式为y=ax2+bx+c.
∴此抛物线的解析式为y=2x2+2x-4.
解法二:∵抛物线过点A(-2,0),B(1,0),
∴设此抛物线的解析式为y=a(x+2)(x-1).
又∵抛物线过点C(2,8),
∴8=a(2+2)×(2-1),解得a=2,
∴y=2(x+2)(x-1)=2x2+2x-4.
即此抛物线的解析式为y=2x2+2x-4.
归纳总结
方法
适用条件及求法
一般式
若已知图象上三个点的坐标,则设所求二次函数的解析式为y=ax2+bx+c,将已知三个点的坐标代入,求a,b,c的值
顶点式
若已知二次函数图象的顶点坐标或对称轴与最大值(或最小值),则设所求二次函数的解析式为y=a(x-h)2+k,将其他已知条件代入,求出待定系数
归纳总结
方法
适用条件及求法
交点式
若已知二次函数图象与x轴的两个交点的坐标为(x1,0),(x2,0),则设所求二次函数的解析式为y=a(x-x1)(x-x2),将其他已知条件代入,求出待定系数
模块4 二次函数的实际应用
在日常生活、生产和科研中,常常会遇到求什么条件下可以使材料最省、时间最少、效率最高等问题,其中一些问题可以归纳为求二次函数的最大值或最小值.请举例说明如何分析、解决这样的问题.
例4
[2020·黄冈]网络销售已经成为一种热门的销售方式.为了减少农产品的库存,我市市长亲自在某网络平台上进行直播销售大别山牌板栗.为提高大家购买的积极性,直播时,板栗公司每天拿出2000元现金,作为红包发给购买者.已知该板栗的成本价格为6元/kg,每日销售量y(kg)与销售单价x(元/kg)满足关系式:y=-100x+5000.经销售发现,销售单价不低于成本价且不高于30元/kg.当每日销售量不低于4000
kg时,每千克成本将降低1元.设板栗公司销售该板栗的日获利为W(元).
(1)请求出日获利W与销售单价x之间的函数关系式;
(2)当销售单价定为多少时,销售这种板栗日获利最大?最大利润为多少元?
(3)当W≥40000元时,网络平台将向板栗公司收取a元/kg(a<4)的相关费用,若此时日获利的最大值为42100元,求a的值.
解:(1)当y≥4000时,-100x+5000≥4000,解得x≤10.
∴当6≤x≤10时,W=(x-6+1)(-100x+5000)-2000=-100x2+5500x-27000;
当10<x≤30时,W=(x-6)(-100x+5000)-2000=-100x2+5600x-32000.
(2)当6≤x≤10时,W=-100x2+5500x-27000.
∴当x=10时,W最大=-100×102+5500×10-27000=18000.
当10<x≤30时,W=-100x2+5600x-32000.
∵图象的对称轴为直线x=28,
∴当x=28时,W最大=-100×282+5600×28-32000=46400.
∵46400>18000,∴当销售单价定为28元/kg时,销售这种板栗日获利最大,最大利润为46400元.
(3)∵40000>18000,
∴10<x≤30,则W=-100x2+5600x-32000.
令W=40000,则-100x2+5600x-32000=40000,解得x1=20,x2=36.
在平面直角坐标系中,画出函数
W=-100x2+5600x-32000的
大致图象如图所示.
观察图象可知,当W≥40000时,20≤x≤36.
又∵10<x≤30,∴20≤x≤30.
设现在板栗公司销售该板栗的日获利为W1元,则W1=(x-6-a)(-100x+5000)-2000=-100x2+(5600+100a)x-32000-5000a,
整理得a2-88a+172=0,解得a1=2,a2=86.
又∵a<4,∴a=2.
模块5 数学思想方法的应用
通过本章的学习,你领悟了哪些数学思想方法?你能举例说明数学思想方法在解题中的应用吗?
例5
[数形结合思想]对于题目“一段抛物线L:y=-x(x-3)+c(0≤x≤3)与直线l:y=x+2有唯一公共点,若c为整数,确定所有c的值.”甲的结果是c=1,乙的结果是c=3或4.则( )
A.甲的结果正确
B.乙的结果正确
C.甲、乙的结果合在一起才正确
D.甲、乙的结果合在一起也不正确
D
(1)当c<1时,L与l没有公共点;
(2)当c=1时,L与l有一个公共点;
(3)当1<c≤2时,L与l有两个公共点;
(4)当2<c≤5时,L与l有一个公共点;
(5)当c>5时,L与l没有公共点.
所以当整数c=1,3,4,5时,L与l有一个公共点.故选D.
一、二次函数与代数综合
例6
已知关于x的一元二次方程mx2+(1-5m)x-5=0(m≠0).
(1)求证:无论m为何非零实数,此方程总有两个实数根;
(2)若抛物线y=mx2+(1-5m)x-5与x轴交于A(x1,0),B(x2,0)两点,且|x1-x2|=6,求m的值;
(3)若m>0,点P(a,b)与点Q(a+n,b)在(2)中的抛物线上(点P,Q不重合),求代数式4a2-n2+8n的值.
解:(1)证明:∵Δ=(1-5m)2-4m·(-5)=(5m+1)2≥0,
∴无论m为何非零实数,此方程总有两个实数根.
(2)在y=mx2+(1-5m)x-5中,令y=0,
则mx2+(1-5m)x-5=0.
将方程mx2+(1-5m)x-5=0左边分解因式,得(mx+1)(x-5)=0.
(3)由(2)得,当m>0时,m=1,
此时抛物线为y=x2-4x-5,其对称轴为直线x=2.
由题意知,点P,Q关于直线x=2对称,
∴4a2-n2+8n=(4-n)2-n2+8n=16.
二、二次函数与几何综合
例7
如图22-T-3,在平面直角坐标系中,二次函数y=ax2+bx+c的图象交x轴于点A(-4,0),B(2,0),交y轴于点C(0,6),在y轴上有一点E(0,-2),连接AE.
(1)求二次函数的解析式.
图22-T-3
(2)若点D在第二象限且是抛物线上的一个动点,求△ADE面积的最大值.
(3)抛物线的对称轴上是否存在点P,使
△AEP为等腰三角形?若存在,请直接写
出所有点P的坐标;若不存在,请说明
理由.
图22-T-3
解:(1)由题意可得
如图,过点D作DF∥y轴交AE于点F,交x轴于点G,过点E作EH⊥
DF,垂足为H.
三边均不与坐标轴平行的三角形面积的计算方法
(1)从铅直方向(或水平方向)确定三个顶点中哪个居中;
(2)过居中的顶点作横轴(或纵轴)的垂线,从而把原三角形分
成易于计算面积的两个小三角形.
归纳总结
归纳总结
图22-T-4
https://www.21cnjy.com/help/help_extract.php
本章总结提升
第二十二章
二次函数
本章总结提升
知识结构关系
重点模块总结
综合能力提升
第二十二章 二次函数
图形面积
销售利润
抛物线形
实际问题
实际问题
的答案
目标
归纳
抽象
二次函数y=
ax2+bx+c
利用二次函数的
图象和性质求解
y=0
一元二次方程
ax+
bx+c=0
图象
性质
y=a(x-h)2+k
左右平移
上下平移
y=ax2+k
y=a(x-h)2
上下平移
左右平移
y=ax2
模块1 抛物线的平移
抛物线y=ax2经过怎样的平移可以得到抛物线y=a(x-h)2+k?
例1
(1)[2020·绥化]将抛物线y=2(x-3)2+2向左平移3个单位长度,再向下平移2个单位长度,得到的抛物线的解析式是
( )
A.y=2(x-6)2
B.y=2(x-6)2+4
C.y=2x2
D.y=2x2+4
C
(2)若将抛物线y=ax2+bx+c向下平移3个单位长度,再向左平移1个单位长度得到抛物线y=2(x-1)2+3,则a=_______,
b=________,c=________.
[解析]
∵平移前后抛物线的开口方向和大小相同,∴a=2.依题意可知,平移前的抛物线的顶点坐标是(2,6),∴平移前的抛物线的解析式为y=2(x-2)2+6,即y=2x2-8x+14,∴b=-8,c=14.
2
-8
14
将抛物线y=ax2+bx+c用配方法化成y=a(x-h)2+k的形式,而任意抛物线y=a(x-h)2+k均可由抛物线y=ax2平移得到,具体平移方法如图22-T-1:
归纳总结
图22-T-1
模块2 二次函数的图象和性质
结合二次函数的图象回顾二次函数的性质,例如根据抛物线的开口方向、顶点坐标,说明二次函数在什么情况下取得最大(小)值.
例2
[2020·襄阳]二次函数y=ax2+bx+c的图象如图22-T-2所示,有下列结论:①ac<0;②3a+c=0;③4ac-b2<0;④当x>-1时,y随着x的增大而减小.其中正确的有
( )
A.4个
B.3个
C.2个
D.1个
图22-T-2
B
归纳总结
y=ax2+bx+c
字母的符号
图象的特征
a
a>0
开口向上
a<0
开口向下
b
b=0
对称轴为y轴
ab>0(a与b同号)
对称轴在y轴左侧
ab<0(a与b异号)
对称轴在y轴右侧
归纳总结
y=ax2+bx+c
字母的符号
图象的特征
c
c=0
经过原点
c>0
与y轴正半轴相交
c<0
与y轴负半轴相交
归纳总结
y=ax2+bx+c
字母的符号
图象的特征
b2-4ac
b2-4ac=0
与x轴有唯一公共点(顶点)
b2-4ac>0
与x轴有两个公共点
b2-4ac<0
与x轴没有公共点
归纳总结
特殊关系
当x=1时,y=a+b+c;
当x=-1时,y=a-b+c;
若a+b+c>0,则当x=1时,y>0;
若a-b+c>0,则当x=-1时,y>0
模块3 用待定系数法求二次函数的解析式
用待定系数法求二次函数的解析式的方法有哪些?
例3
已知一抛物线与x轴的交点是A(-2,0),B(1,0),且经过点C(2,8),求此抛物线的解析式.
[解析]
已知此抛物线经过三点,故可设一般式求解析式.若仔细观察点A,B的特征,又知点A,B是抛物线与x轴的交点,因此又可设交点式求解析式.
解:解法一:设此抛物线的解析式为y=ax2+bx+c.
∴此抛物线的解析式为y=2x2+2x-4.
解法二:∵抛物线过点A(-2,0),B(1,0),
∴设此抛物线的解析式为y=a(x+2)(x-1).
又∵抛物线过点C(2,8),
∴8=a(2+2)×(2-1),解得a=2,
∴y=2(x+2)(x-1)=2x2+2x-4.
即此抛物线的解析式为y=2x2+2x-4.
归纳总结
方法
适用条件及求法
一般式
若已知图象上三个点的坐标,则设所求二次函数的解析式为y=ax2+bx+c,将已知三个点的坐标代入,求a,b,c的值
顶点式
若已知二次函数图象的顶点坐标或对称轴与最大值(或最小值),则设所求二次函数的解析式为y=a(x-h)2+k,将其他已知条件代入,求出待定系数
归纳总结
方法
适用条件及求法
交点式
若已知二次函数图象与x轴的两个交点的坐标为(x1,0),(x2,0),则设所求二次函数的解析式为y=a(x-x1)(x-x2),将其他已知条件代入,求出待定系数
模块4 二次函数的实际应用
在日常生活、生产和科研中,常常会遇到求什么条件下可以使材料最省、时间最少、效率最高等问题,其中一些问题可以归纳为求二次函数的最大值或最小值.请举例说明如何分析、解决这样的问题.
例4
[2020·黄冈]网络销售已经成为一种热门的销售方式.为了减少农产品的库存,我市市长亲自在某网络平台上进行直播销售大别山牌板栗.为提高大家购买的积极性,直播时,板栗公司每天拿出2000元现金,作为红包发给购买者.已知该板栗的成本价格为6元/kg,每日销售量y(kg)与销售单价x(元/kg)满足关系式:y=-100x+5000.经销售发现,销售单价不低于成本价且不高于30元/kg.当每日销售量不低于4000
kg时,每千克成本将降低1元.设板栗公司销售该板栗的日获利为W(元).
(1)请求出日获利W与销售单价x之间的函数关系式;
(2)当销售单价定为多少时,销售这种板栗日获利最大?最大利润为多少元?
(3)当W≥40000元时,网络平台将向板栗公司收取a元/kg(a<4)的相关费用,若此时日获利的最大值为42100元,求a的值.
解:(1)当y≥4000时,-100x+5000≥4000,解得x≤10.
∴当6≤x≤10时,W=(x-6+1)(-100x+5000)-2000=-100x2+5500x-27000;
当10<x≤30时,W=(x-6)(-100x+5000)-2000=-100x2+5600x-32000.
(2)当6≤x≤10时,W=-100x2+5500x-27000.
∴当x=10时,W最大=-100×102+5500×10-27000=18000.
当10<x≤30时,W=-100x2+5600x-32000.
∵图象的对称轴为直线x=28,
∴当x=28时,W最大=-100×282+5600×28-32000=46400.
∵46400>18000,∴当销售单价定为28元/kg时,销售这种板栗日获利最大,最大利润为46400元.
(3)∵40000>18000,
∴10<x≤30,则W=-100x2+5600x-32000.
令W=40000,则-100x2+5600x-32000=40000,解得x1=20,x2=36.
在平面直角坐标系中,画出函数
W=-100x2+5600x-32000的
大致图象如图所示.
观察图象可知,当W≥40000时,20≤x≤36.
又∵10<x≤30,∴20≤x≤30.
设现在板栗公司销售该板栗的日获利为W1元,则W1=(x-6-a)(-100x+5000)-2000=-100x2+(5600+100a)x-32000-5000a,
整理得a2-88a+172=0,解得a1=2,a2=86.
又∵a<4,∴a=2.
模块5 数学思想方法的应用
通过本章的学习,你领悟了哪些数学思想方法?你能举例说明数学思想方法在解题中的应用吗?
例5
[数形结合思想]对于题目“一段抛物线L:y=-x(x-3)+c(0≤x≤3)与直线l:y=x+2有唯一公共点,若c为整数,确定所有c的值.”甲的结果是c=1,乙的结果是c=3或4.则( )
A.甲的结果正确
B.乙的结果正确
C.甲、乙的结果合在一起才正确
D.甲、乙的结果合在一起也不正确
D
(1)当c<1时,L与l没有公共点;
(2)当c=1时,L与l有一个公共点;
(3)当1<c≤2时,L与l有两个公共点;
(4)当2<c≤5时,L与l有一个公共点;
(5)当c>5时,L与l没有公共点.
所以当整数c=1,3,4,5时,L与l有一个公共点.故选D.
一、二次函数与代数综合
例6
已知关于x的一元二次方程mx2+(1-5m)x-5=0(m≠0).
(1)求证:无论m为何非零实数,此方程总有两个实数根;
(2)若抛物线y=mx2+(1-5m)x-5与x轴交于A(x1,0),B(x2,0)两点,且|x1-x2|=6,求m的值;
(3)若m>0,点P(a,b)与点Q(a+n,b)在(2)中的抛物线上(点P,Q不重合),求代数式4a2-n2+8n的值.
解:(1)证明:∵Δ=(1-5m)2-4m·(-5)=(5m+1)2≥0,
∴无论m为何非零实数,此方程总有两个实数根.
(2)在y=mx2+(1-5m)x-5中,令y=0,
则mx2+(1-5m)x-5=0.
将方程mx2+(1-5m)x-5=0左边分解因式,得(mx+1)(x-5)=0.
(3)由(2)得,当m>0时,m=1,
此时抛物线为y=x2-4x-5,其对称轴为直线x=2.
由题意知,点P,Q关于直线x=2对称,
∴4a2-n2+8n=(4-n)2-n2+8n=16.
二、二次函数与几何综合
例7
如图22-T-3,在平面直角坐标系中,二次函数y=ax2+bx+c的图象交x轴于点A(-4,0),B(2,0),交y轴于点C(0,6),在y轴上有一点E(0,-2),连接AE.
(1)求二次函数的解析式.
图22-T-3
(2)若点D在第二象限且是抛物线上的一个动点,求△ADE面积的最大值.
(3)抛物线的对称轴上是否存在点P,使
△AEP为等腰三角形?若存在,请直接写
出所有点P的坐标;若不存在,请说明
理由.
图22-T-3
解:(1)由题意可得
如图,过点D作DF∥y轴交AE于点F,交x轴于点G,过点E作EH⊥
DF,垂足为H.
三边均不与坐标轴平行的三角形面积的计算方法
(1)从铅直方向(或水平方向)确定三个顶点中哪个居中;
(2)过居中的顶点作横轴(或纵轴)的垂线,从而把原三角形分
成易于计算面积的两个小三角形.
归纳总结
归纳总结
图22-T-4
https://www.21cnjy.com/help/help_extract.php
同课章节目录
