【人教九上数学学霸提升作业】22.1.3 第3课时 二次函数y=a(x-h)2+k的图象和性质(含答案)
文档属性
| 名称 | 【人教九上数学学霸提升作业】22.1.3 第3课时 二次函数y=a(x-h)2+k的图象和性质(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第3课时 二次函数y=a(x-h)2+k的图象和性质
命题点
1 二次函数y=a(x-h)2+k的图象和性质
1.二次函数y=(x+2)2-1的图象大致为图22-1-23中的
( )
图22-1-23
2.[2020·凉山州模拟]
下列关于二次函数y=2(x-3)2+2的说法正确的是
( )
A.其图象的顶点坐标为(-3,2)
B.其图象的对称轴是直线y=3
C.当x>3时,y随x的增大而增大
D.当x=0时,y=2
3.[2020·甘孜州]
如图22-1-24,二次函数y=a(x+1)2+k的图象与x轴交于A(-3,0),B两点,下列说法错误的是
( )
A.a<0
B.图象的对称轴为直线x=-1
C.点B的坐标为(1,0)
D.当x<0时,y随x的增大而增大
图22-1-24
图22-1-25
4.图22-1-25中是有相同对称轴的两条抛物线,下列关系不正确的是
( )
A.h=m
B.k>n
C.k=n
D.h>0,k>0
5.已知二次函数y=a(x+k)2+k(a≠0),无论k取何值,其图象的顶点都在
( )
A.直线y=x上
B.直线y=-x上
C.x轴上
D.y轴上
6.已知二次函数y=-(x-1)2+3,当t( )
A.t<0
B.0≤t<1
C.1≤t<4
D.t≥4
7.已知点A(4,y1),B(,y2),C(-2,y3)都在二次函数y=(x-2)2-1的图象上,则y1,y2,y3的大小关系是 .(用“>”号连接)?
命题点
2 二次函数y=a(x-h)2+k与y=ax2的关系
8.将抛物线y=2(x-4)2-1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为
( )
A.y=2x2+1
B.y=2x2-3
C.y=2(x-8)2+1
D.y=2(x-8)2-3
9.[2020·衢州]
二次函数y=x2的图象平移后经过点(2,0),则下列平移方法正确的是
( )
A.向左平移2个单位长度,向下平移2个单位长度
B.向左平移1个单位长度,向上平移2个单位长度
C.向右平移1个单位长度,向下平移1个单位长度
D.向右平移2个单位长度,向上平移1个单位长度
10.若抛物线y=(x-1)2+2不动,将平面直角坐标系xOy先沿水平方向向右平移1个单位长度,再沿铅直方向向上平移3个单位长度,则原抛物线的解析式变为
( )
A.y=(x-2)2+3
B.y=(x-2)2+5
C.y=x2-1
D.y=x2+4
11.[2020·牡丹江]
将抛物线y=(x-1)2-5关于y轴对称,再向右平移3个单位长度后顶点的坐标是 .?
12.如图22-1-26,把抛物线y=x2平移得到抛物线m,抛物线m经过点A(-6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q.
图22-1-26
(1)求顶点P的坐标;
(2)写出平移过程;
(3)求图中阴影部分的面积.
命题点
3 确定y=a(x-h)2+k的解析式
13.图象的顶点为M(-2,1),且经过原点的二次函数解析式是
( )
A.y=(x-2)2+1
B.y=-(x+2)2+1
C.y=(x+2)2+1
D.y=(x-2)2+1
14.随着新农村的建设和旧城的改造,我们的家园越来越美丽.小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高为2
m的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为1
m处达到最高,水柱落地处离池中心3
m.(如图22-1-27所示)
(1)请你建立适当的平面直角坐标系,并求出水柱抛物线的解析式;
(2)求水柱的最大高度.
图22-1-27
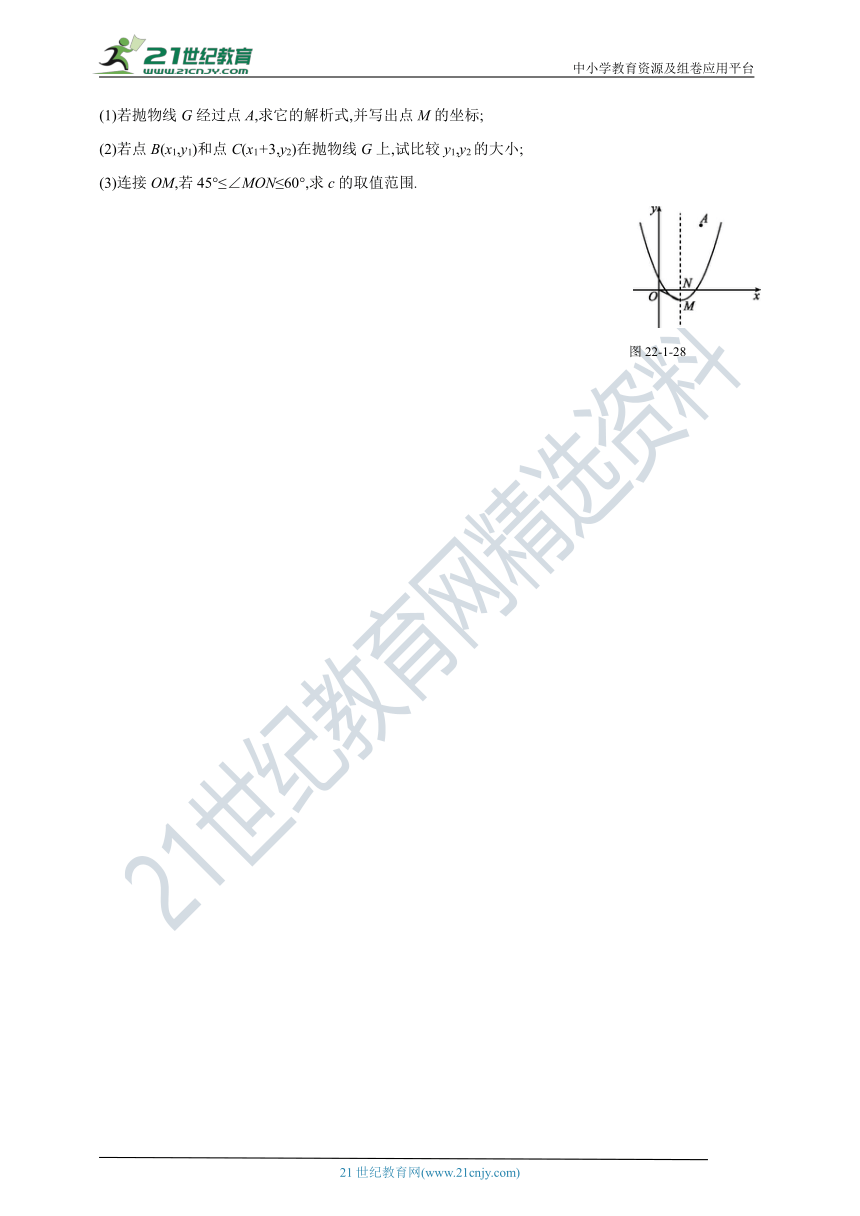
15.如图22-1-28,在平面直角坐标系中,点A(2,3),抛物线G:y=x2-2x+c(c为常数)的顶点为M,对称轴与x轴相交于点N.
(1)若抛物线G经过点A,求它的解析式,并写出点M的坐标;
(2)若点B(x1,y1)和点C(x1+3,y2)在抛物线G上,试比较y1,y2的大小;
(3)连接OM,若45°≤∠MON≤60°,求c的取值范围.
图22-1-28
典题讲评与答案详析
1.D 2.C 3.D
4.C [解析]
因为这两条抛物线的对称轴是同一条直线,所以h=m.而顶点(h,k)在顶点(m,n)的上方,因此有k>n.观察图象可知对称轴x=h在y轴的右侧,因此有h>0,顶点(h,k)在x轴的上方,因此有k>0.
5.B 6.C
7.y3>y1>y2 [解析]
先找到抛物线y=(x-2)2-1的对称轴为直线x=2,再找到点(4,y1)关于直线x=2的对称点为(0,y1),最后利用x<2时,y随x的增大而减小解题.因为-2<0<,所以有y3>y1>y2.
8.A [解析]
抛物线y=2(x-4)2-1先向左平移4个单位长度,得到的抛物线的解析式为y=2(x-4+4)2-1,即y=2x2-1,再向上平移2个单位长度得到的抛物线的解析式为y=2x2-1+2,即y=2x2+1.
9.C [解析]
按A选项中的方法平移后所得的二次函数图象的解析式为y=(x+2)2-2,当x=2时,y=14,所以图象不经过点(2,0);
按B选项中的方法平移后所得的二次函数图象的解析式为y=(x+1)2+2,
当x=2时,y=11,所以图象不经过点(2,0);
按C选项中的方法平移后所得的二次函数图象的解析式为y=(x-1)2-1,
当x=2时,y=0,所以图象经过点(2,0);
按D选项中的方法平移后所得的二次函数图象的解析式为y=(x-2)2+1,
当x=2时,y=1,所以图象不经过点(2,0).
因此本题选C.
10.C [解析]
将平面直角坐标系xOy先沿水平方向向右平移1个单位长度,再沿铅直方向向上平移3个单位长度,这相当于平面直角坐标系不动,把抛物线向左平移1个单位长度,再向下平移3个单位长度.
∵y=(x-1)2+2,
∴原抛物线的解析式变为y=(x-1+1)2+2-3=x2-1.
11.(2,-5)
12.解:(1)设P(h,k),则抛物线m的解析式为y=(x-h)2+k.
∵抛物线m经过点A(-6,0)和原点O(0,0),
∴0=(-6-h)2+k,0=(0-h)2+k,
解得h=-3,k=-,∴y=(x+3)2-.
∴顶点P的坐标为-3,-.
(2)答案不唯一,如抛物线y=x2向左平移3个单位长度,再向下平移个单位长度.
(3)连接OP,OQ.
∵抛物线m的对称轴与抛物线y=x2交于点Q,
∴Q-3,,
∴点P,Q关于x轴对称,
∴图中阴影部分的面积=S△OPQ=×3×9=.
13.B
14.解:(1)答案不唯一,如:如图所示,以喷水管与地面交点为原点,原点与水柱落地点所在直线为x轴,喷水管所在直线为y轴,建立平面直角坐标系.
设抛物线的解析式为y=a(x-1)2+k,代入(0,2)和(3,0),得解得
∴水柱抛物线的解析式为y=-(x-1)2+(0≤x≤3).
(2)∵y=-(x-1)2+(0≤x≤3),
∴当x=1时,y取得最大值,最大值为,即水柱的最大高度为
m.
15.解:(1)∵抛物线y=x2-2x+c经过点A(2,3),
∴3=22-2×2+c,∴c=3,
∴抛物线G的解析式为y=x2-2x+3.
∵y=x2-2x+3=(x-1)2+2,
∴点M的坐标为(1,2).
(2)∵点B(x1,y1)和点C(x1+3,y2)在抛物线G上,
∴y1=-2x1+c,y2=(x1+3)2-2(x1+3)+c,
∴y2-y1=(x1+3)2-2(x1+3)+c-(-2x1+c)=6x1+3.
当x1>-时,y2>y1;
当x1=-时,y2=y1;
当x1<-时,y2(3)∵y=x2-2x+c=(x-1)2+c-1,
∴N(1,0),∴ON=1.
当点M在x轴上方时,若∠MON=45°,如图①,
则ON=MN=1,∴M(1,1),
∴1=(1-1)2+c-1,∴c=2;
若∠MON=60°,如图②,
则MN=ON=,
∴M(1,),
∴=(1-1)2+c-1,∴c=+1.
∴若45°≤∠MON≤60°,则2≤c≤+1.
同理,当点M在x轴下方时,-+1≤c≤0.
综上,当45°≤∠MON≤60°时,c的取值范围为2≤c≤+1或-+1≤c≤0.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
第3课时 二次函数y=a(x-h)2+k的图象和性质
命题点
1 二次函数y=a(x-h)2+k的图象和性质
1.二次函数y=(x+2)2-1的图象大致为图22-1-23中的
( )
图22-1-23
2.[2020·凉山州模拟]
下列关于二次函数y=2(x-3)2+2的说法正确的是
( )
A.其图象的顶点坐标为(-3,2)
B.其图象的对称轴是直线y=3
C.当x>3时,y随x的增大而增大
D.当x=0时,y=2
3.[2020·甘孜州]
如图22-1-24,二次函数y=a(x+1)2+k的图象与x轴交于A(-3,0),B两点,下列说法错误的是
( )
A.a<0
B.图象的对称轴为直线x=-1
C.点B的坐标为(1,0)
D.当x<0时,y随x的增大而增大
图22-1-24
图22-1-25
4.图22-1-25中是有相同对称轴的两条抛物线,下列关系不正确的是
( )
A.h=m
B.k>n
C.k=n
D.h>0,k>0
5.已知二次函数y=a(x+k)2+k(a≠0),无论k取何值,其图象的顶点都在
( )
A.直线y=x上
B.直线y=-x上
C.x轴上
D.y轴上
6.已知二次函数y=-(x-1)2+3,当t
A.t<0
B.0≤t<1
C.1≤t<4
D.t≥4
7.已知点A(4,y1),B(,y2),C(-2,y3)都在二次函数y=(x-2)2-1的图象上,则y1,y2,y3的大小关系是 .(用“>”号连接)?
命题点
2 二次函数y=a(x-h)2+k与y=ax2的关系
8.将抛物线y=2(x-4)2-1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为
( )
A.y=2x2+1
B.y=2x2-3
C.y=2(x-8)2+1
D.y=2(x-8)2-3
9.[2020·衢州]
二次函数y=x2的图象平移后经过点(2,0),则下列平移方法正确的是
( )
A.向左平移2个单位长度,向下平移2个单位长度
B.向左平移1个单位长度,向上平移2个单位长度
C.向右平移1个单位长度,向下平移1个单位长度
D.向右平移2个单位长度,向上平移1个单位长度
10.若抛物线y=(x-1)2+2不动,将平面直角坐标系xOy先沿水平方向向右平移1个单位长度,再沿铅直方向向上平移3个单位长度,则原抛物线的解析式变为
( )
A.y=(x-2)2+3
B.y=(x-2)2+5
C.y=x2-1
D.y=x2+4
11.[2020·牡丹江]
将抛物线y=(x-1)2-5关于y轴对称,再向右平移3个单位长度后顶点的坐标是 .?
12.如图22-1-26,把抛物线y=x2平移得到抛物线m,抛物线m经过点A(-6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q.
图22-1-26
(1)求顶点P的坐标;
(2)写出平移过程;
(3)求图中阴影部分的面积.
命题点
3 确定y=a(x-h)2+k的解析式
13.图象的顶点为M(-2,1),且经过原点的二次函数解析式是
( )
A.y=(x-2)2+1
B.y=-(x+2)2+1
C.y=(x+2)2+1
D.y=(x-2)2+1
14.随着新农村的建设和旧城的改造,我们的家园越来越美丽.小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高为2
m的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为1
m处达到最高,水柱落地处离池中心3
m.(如图22-1-27所示)
(1)请你建立适当的平面直角坐标系,并求出水柱抛物线的解析式;
(2)求水柱的最大高度.
图22-1-27
15.如图22-1-28,在平面直角坐标系中,点A(2,3),抛物线G:y=x2-2x+c(c为常数)的顶点为M,对称轴与x轴相交于点N.
(1)若抛物线G经过点A,求它的解析式,并写出点M的坐标;
(2)若点B(x1,y1)和点C(x1+3,y2)在抛物线G上,试比较y1,y2的大小;
(3)连接OM,若45°≤∠MON≤60°,求c的取值范围.
图22-1-28
典题讲评与答案详析
1.D 2.C 3.D
4.C [解析]
因为这两条抛物线的对称轴是同一条直线,所以h=m.而顶点(h,k)在顶点(m,n)的上方,因此有k>n.观察图象可知对称轴x=h在y轴的右侧,因此有h>0,顶点(h,k)在x轴的上方,因此有k>0.
5.B 6.C
7.y3>y1>y2 [解析]
先找到抛物线y=(x-2)2-1的对称轴为直线x=2,再找到点(4,y1)关于直线x=2的对称点为(0,y1),最后利用x<2时,y随x的增大而减小解题.因为-2<0<,所以有y3>y1>y2.
8.A [解析]
抛物线y=2(x-4)2-1先向左平移4个单位长度,得到的抛物线的解析式为y=2(x-4+4)2-1,即y=2x2-1,再向上平移2个单位长度得到的抛物线的解析式为y=2x2-1+2,即y=2x2+1.
9.C [解析]
按A选项中的方法平移后所得的二次函数图象的解析式为y=(x+2)2-2,当x=2时,y=14,所以图象不经过点(2,0);
按B选项中的方法平移后所得的二次函数图象的解析式为y=(x+1)2+2,
当x=2时,y=11,所以图象不经过点(2,0);
按C选项中的方法平移后所得的二次函数图象的解析式为y=(x-1)2-1,
当x=2时,y=0,所以图象经过点(2,0);
按D选项中的方法平移后所得的二次函数图象的解析式为y=(x-2)2+1,
当x=2时,y=1,所以图象不经过点(2,0).
因此本题选C.
10.C [解析]
将平面直角坐标系xOy先沿水平方向向右平移1个单位长度,再沿铅直方向向上平移3个单位长度,这相当于平面直角坐标系不动,把抛物线向左平移1个单位长度,再向下平移3个单位长度.
∵y=(x-1)2+2,
∴原抛物线的解析式变为y=(x-1+1)2+2-3=x2-1.
11.(2,-5)
12.解:(1)设P(h,k),则抛物线m的解析式为y=(x-h)2+k.
∵抛物线m经过点A(-6,0)和原点O(0,0),
∴0=(-6-h)2+k,0=(0-h)2+k,
解得h=-3,k=-,∴y=(x+3)2-.
∴顶点P的坐标为-3,-.
(2)答案不唯一,如抛物线y=x2向左平移3个单位长度,再向下平移个单位长度.
(3)连接OP,OQ.
∵抛物线m的对称轴与抛物线y=x2交于点Q,
∴Q-3,,
∴点P,Q关于x轴对称,
∴图中阴影部分的面积=S△OPQ=×3×9=.
13.B
14.解:(1)答案不唯一,如:如图所示,以喷水管与地面交点为原点,原点与水柱落地点所在直线为x轴,喷水管所在直线为y轴,建立平面直角坐标系.
设抛物线的解析式为y=a(x-1)2+k,代入(0,2)和(3,0),得解得
∴水柱抛物线的解析式为y=-(x-1)2+(0≤x≤3).
(2)∵y=-(x-1)2+(0≤x≤3),
∴当x=1时,y取得最大值,最大值为,即水柱的最大高度为
m.
15.解:(1)∵抛物线y=x2-2x+c经过点A(2,3),
∴3=22-2×2+c,∴c=3,
∴抛物线G的解析式为y=x2-2x+3.
∵y=x2-2x+3=(x-1)2+2,
∴点M的坐标为(1,2).
(2)∵点B(x1,y1)和点C(x1+3,y2)在抛物线G上,
∴y1=-2x1+c,y2=(x1+3)2-2(x1+3)+c,
∴y2-y1=(x1+3)2-2(x1+3)+c-(-2x1+c)=6x1+3.
当x1>-时,y2>y1;
当x1=-时,y2=y1;
当x1<-时,y2
∴N(1,0),∴ON=1.
当点M在x轴上方时,若∠MON=45°,如图①,
则ON=MN=1,∴M(1,1),
∴1=(1-1)2+c-1,∴c=2;
若∠MON=60°,如图②,
则MN=ON=,
∴M(1,),
∴=(1-1)2+c-1,∴c=+1.
∴若45°≤∠MON≤60°,则2≤c≤+1.
同理,当点M在x轴下方时,-+1≤c≤0.
综上,当45°≤∠MON≤60°时,c的取值范围为2≤c≤+1或-+1≤c≤0.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
同课章节目录
