1.2怎样判定三角形相似习题精练-普通用卷2021-2022学年九年级数学青岛版上册(Word版 含答案)
文档属性
| 名称 | 1.2怎样判定三角形相似习题精练-普通用卷2021-2022学年九年级数学青岛版上册(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 265.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 12:38:47 | ||
图片预览



文档简介
青岛版九年级上册第一章1.2怎样判定三角形相似习题精练
一、选择题
如图,已知∽,且,则等于?
?
A.
B.
C.
D.
如图,∽,下列各式中正确的有?
?
.
A.
1个
B.
2个
C.
3个
D.
4个
如图,D是的边BC上的点,∽,则下列各式中正确的是?
?
A.
B.
C.
D.
如图,∽,若,,则与的相似比是?
?
A.
B.
C.
D.
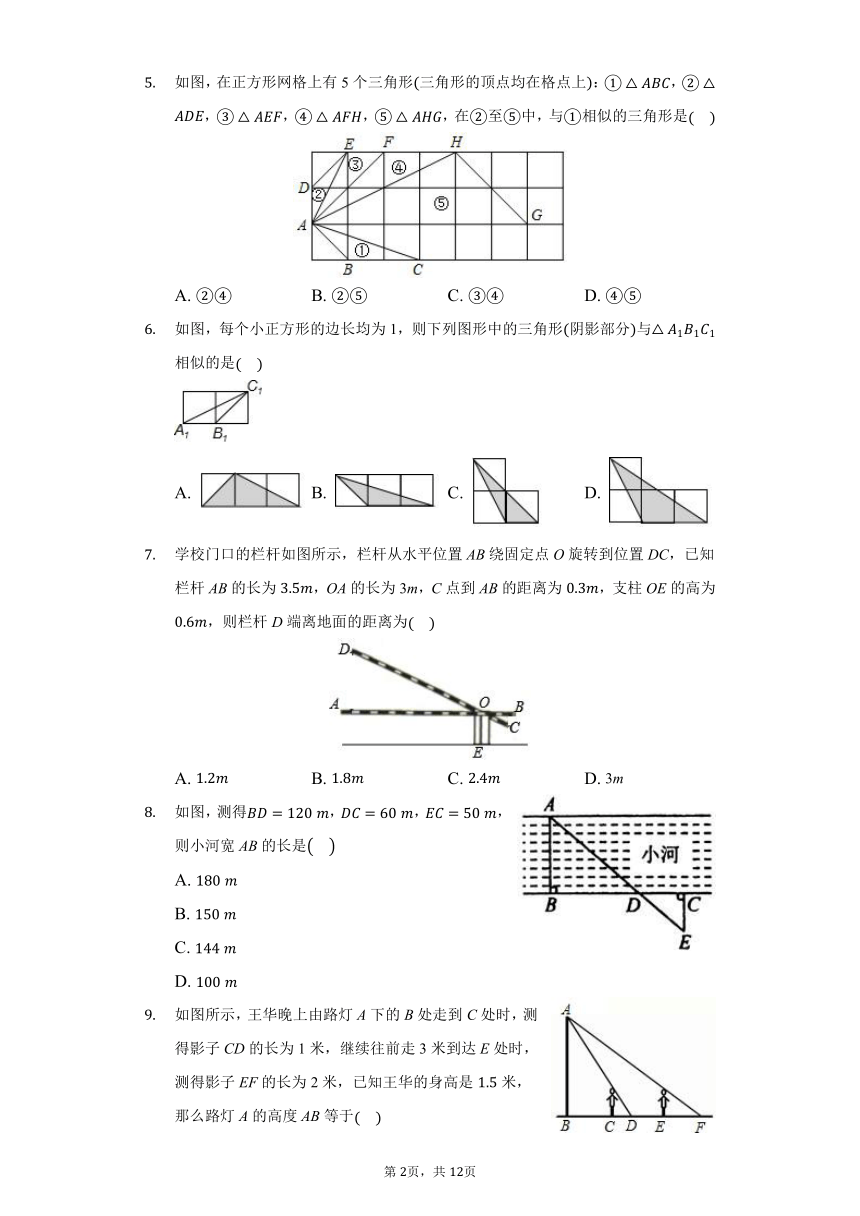
如图,在正方形网格上有5个三角形三角形的顶点均在格点上:,,,,,在至中,与相似的三角形是
A.
B.
C.
D.
如图,每个小正方形的边长均为1,则下列图形中的三角形阴影部分与相似的是
A.
B.
C.
D.
学校门口的栏杆如图所示,栏杆从水平位置AB绕固定点O旋转到位置DC,已知栏杆AB的长为,OA的长为3m,C点到AB的距离为,支柱OE的高为,则栏杆D端离地面的距离为
A.
B.
C.
D.
3m
如图,测得,,,则小河宽AB的长是
A.
B.
C.
D.
如图所示,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是米,那么路灯A的高度AB等于
A.
米
B.
6米
C.
米
D.
8米
如图,P是斜边BC上一点,不与B,C重合,过点P作直线截,使截得的三角形与相似,满足这样的直线共有
A.
1条
B.
2条
C.
3条
D.
4条
二、填空题
在由边长为1的小正方形组成的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形如图,已知是网格图形中的格点三角形,则该图中所有与相似的格点三角形中面积最大的三角形的斜边长是??????????.
如图,的顶点在的正方形网格的格点上,在图中画出一个与相似但不全等的的顶点在格点上,则的最长边是________.
佳佳和琪琪各自制作了一个三角形框架,已知两个三角形框架的形状相同,且佳佳制作的三角形框架的三边长分别为,和,若琪琪制作的三角形框架的最短边长为,则它的最长边长为??????????.
如图是测量河宽的示意图,AE与BC相交于点D,,测得,,,求得河宽______
三、解答题
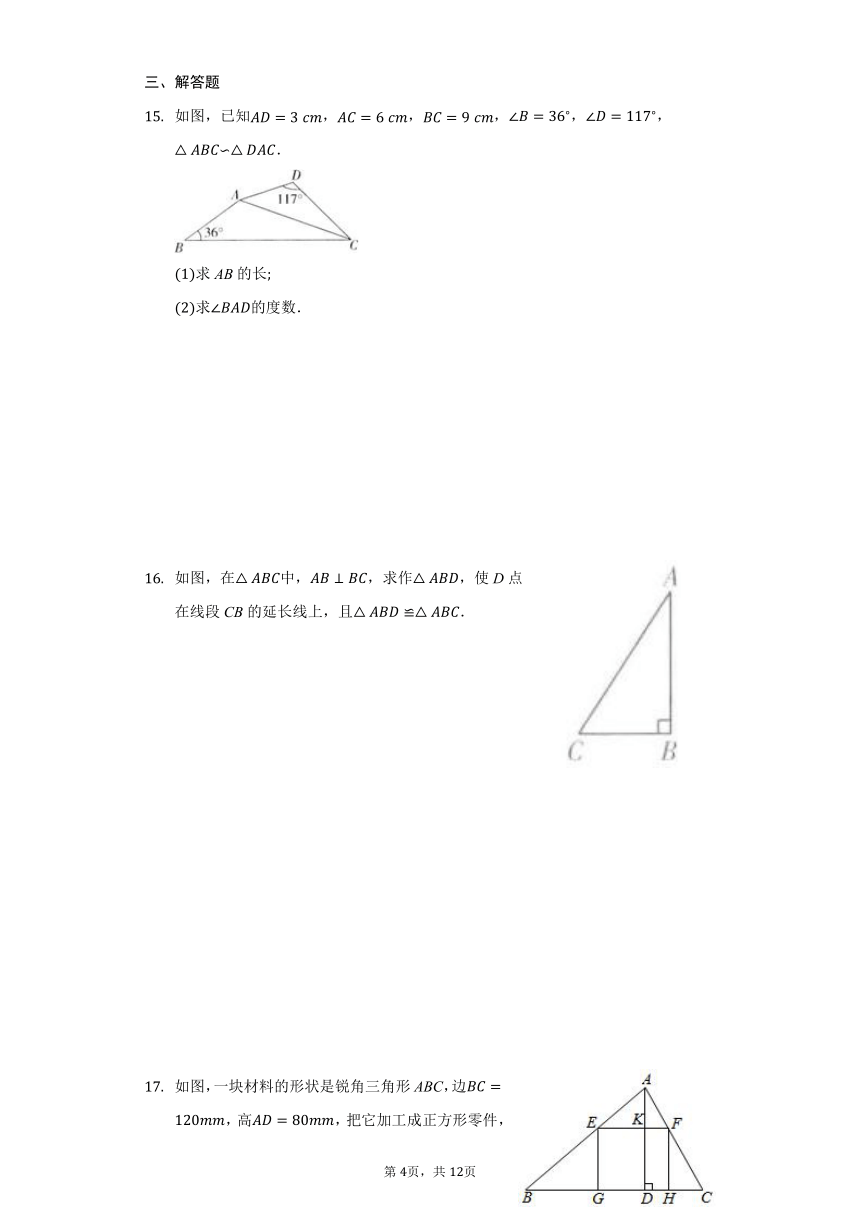
如图,已知,,,,,∽.
求AB的长
求的度数.
如图,在中,,求作,使D点在线段CB的延长线上,且.
如图,一块材料的形状是锐角三角形ABC,边,高,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
已知:如图,中,AD平分,E是AD上一点,且AB::判断BE与BD的数量关系并证明.
已知和点,如图.
以点为一个顶点作,使∽,且的面积等于面积的4倍;要求:尺规作图,不写作法,保留作图痕迹
设D、E、F分别是三边AB、BC、AC的中点,、、分别是你所作的三边、、的中点,求证:∽.
答案和解析
1.【答案】B
【解析】略
2.【答案】A
【解析】错解:D,不能准确找出相似三角形的对应边,从而不能准确写出对应线段所成的比例式.正解:A
3.【答案】D
【解析】?由∽及相似三角形对应边成比例,可得,
只有D选项正确,
故选D.
4.【答案】B
【解析】?,,
,
.
∽,
与的相似比是.
故选B.
5.【答案】A
【解析】解:由题意:中,,
又,
,,
∽∽,
故选:A.
根据两边成比例夹角相等两三角形相似即可判断.
本题考查相似三角形的判定,解题的关键是理解题意,灵活运用所学知识解决问题.
6.【答案】B
【解析】解:因为中有一个角是,四个选项的三角形中,有角的三角形只有B选项的三角形,
且夹角的两边的比相等:,
因此满足了两边对应成比例且夹角相等.
故选:B.
根据相似三角形的判定方法一一判断即可.
7.【答案】C
【解析】解:过D作于G,过C作于H,
则,
∽,
,
栏杆从水平位置AB绕固定点O旋转到位置DC,
,,,
,
,
,
,
栏杆D端离地面的距离为.
故选:C.
过D作于G,过C作于H,则,根据相似三角形的性质即可得到结论.
本题主要考查相似三角形的应用,解题的关键是熟练掌握相似三角形的判定与性质.
8.【答案】D
【解析】解:,,
∽,
,
则,
解得:.
故选D.
此题主要考查了相似三角形的应用;用到的知识点为:两角对应相等的两三角形相似;相似三角形的对应边成比例.由两角对应相等可得∽,利用对应边成比例可得两岸间的大致距离AB.
9.【答案】B
【解析】解:如图,
,
当王华在CG处时,∽,
即,
当王华在EH处时,∽,
即,
,
米,米,米,米,
设,,
,
解得,
则,
解得,米.
即路灯A的高度米.
故选:B.??
10.【答案】C
【解析】解:
由于是直角三角形,
过P点作直线截,则截得的三角形与有一公共角,
所以只要再作一个直角即可使截得的三角形与相似,
过点P可作AB的垂线、AC的垂线、BC的垂线,共3条直线.
故答案选C.??
11.【答案】
【解析】在中,,,
,,与相似的格点三角形的两直角边长的比为,
在的网格图形中,最长线段的长为,此时与相似的三角形较短的直角边长为4,另一直角边长为8,但画不出端点都在格点上且长为8的线段,故较短直角边长应小于4,在图中尝试,可画出,,的三角形DEF,?,
∽,此时为与相似的面积最大的三角形,其斜边长为.
12.【答案】
【解析】解:如图所示:∽,
,,.
的最长边是.
故答案为.
【答案】?
【解析】?设琪琪制作的三角形框架的最长边长为,
根据题意,得,
解得,
即琪琪制作的三角形框架的最长边长为.
14.【答案】100
【解析】解:,,
∽,
,,
解得:米.
故答案为:100.
15.【答案】∽,
,,.
,,,
,
.
.
16.【答案】解:作法如下.
延长
以点B为圆心,以BC长为半径画弧交CB的延长线于点
连接AD,则即为所求作的三角形,如图所示.
17.【答案】解:四边形EGFH为正方形,
,
∽;
设正方形零件的边长为x?mm,则,,
,
∽,
,
,
,
解得:.
答:正方形零件的边长为48mm.
18.【答案】解:.
理由如下:
平分,
,
::AD,
∽,
,
,
.
19.【答案】解:作线段、、,得即可所求.
证明:、、,
∽,
;
证明:
、E、F分别是三边AB、BC、AC的中点,
,,,
∽,
同理:∽,
由可知:∽,
∽.
第2页,共2页
一、选择题
如图,已知∽,且,则等于?
?
A.
B.
C.
D.
如图,∽,下列各式中正确的有?
?
.
A.
1个
B.
2个
C.
3个
D.
4个
如图,D是的边BC上的点,∽,则下列各式中正确的是?
?
A.
B.
C.
D.
如图,∽,若,,则与的相似比是?
?
A.
B.
C.
D.
如图,在正方形网格上有5个三角形三角形的顶点均在格点上:,,,,,在至中,与相似的三角形是
A.
B.
C.
D.
如图,每个小正方形的边长均为1,则下列图形中的三角形阴影部分与相似的是
A.
B.
C.
D.
学校门口的栏杆如图所示,栏杆从水平位置AB绕固定点O旋转到位置DC,已知栏杆AB的长为,OA的长为3m,C点到AB的距离为,支柱OE的高为,则栏杆D端离地面的距离为
A.
B.
C.
D.
3m
如图,测得,,,则小河宽AB的长是
A.
B.
C.
D.
如图所示,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是米,那么路灯A的高度AB等于
A.
米
B.
6米
C.
米
D.
8米
如图,P是斜边BC上一点,不与B,C重合,过点P作直线截,使截得的三角形与相似,满足这样的直线共有
A.
1条
B.
2条
C.
3条
D.
4条
二、填空题
在由边长为1的小正方形组成的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形如图,已知是网格图形中的格点三角形,则该图中所有与相似的格点三角形中面积最大的三角形的斜边长是??????????.
如图,的顶点在的正方形网格的格点上,在图中画出一个与相似但不全等的的顶点在格点上,则的最长边是________.
佳佳和琪琪各自制作了一个三角形框架,已知两个三角形框架的形状相同,且佳佳制作的三角形框架的三边长分别为,和,若琪琪制作的三角形框架的最短边长为,则它的最长边长为??????????.
如图是测量河宽的示意图,AE与BC相交于点D,,测得,,,求得河宽______
三、解答题
如图,已知,,,,,∽.
求AB的长
求的度数.
如图,在中,,求作,使D点在线段CB的延长线上,且.
如图,一块材料的形状是锐角三角形ABC,边,高,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
已知:如图,中,AD平分,E是AD上一点,且AB::判断BE与BD的数量关系并证明.
已知和点,如图.
以点为一个顶点作,使∽,且的面积等于面积的4倍;要求:尺规作图,不写作法,保留作图痕迹
设D、E、F分别是三边AB、BC、AC的中点,、、分别是你所作的三边、、的中点,求证:∽.
答案和解析
1.【答案】B
【解析】略
2.【答案】A
【解析】错解:D,不能准确找出相似三角形的对应边,从而不能准确写出对应线段所成的比例式.正解:A
3.【答案】D
【解析】?由∽及相似三角形对应边成比例,可得,
只有D选项正确,
故选D.
4.【答案】B
【解析】?,,
,
.
∽,
与的相似比是.
故选B.
5.【答案】A
【解析】解:由题意:中,,
又,
,,
∽∽,
故选:A.
根据两边成比例夹角相等两三角形相似即可判断.
本题考查相似三角形的判定,解题的关键是理解题意,灵活运用所学知识解决问题.
6.【答案】B
【解析】解:因为中有一个角是,四个选项的三角形中,有角的三角形只有B选项的三角形,
且夹角的两边的比相等:,
因此满足了两边对应成比例且夹角相等.
故选:B.
根据相似三角形的判定方法一一判断即可.
7.【答案】C
【解析】解:过D作于G,过C作于H,
则,
∽,
,
栏杆从水平位置AB绕固定点O旋转到位置DC,
,,,
,
,
,
,
栏杆D端离地面的距离为.
故选:C.
过D作于G,过C作于H,则,根据相似三角形的性质即可得到结论.
本题主要考查相似三角形的应用,解题的关键是熟练掌握相似三角形的判定与性质.
8.【答案】D
【解析】解:,,
∽,
,
则,
解得:.
故选D.
此题主要考查了相似三角形的应用;用到的知识点为:两角对应相等的两三角形相似;相似三角形的对应边成比例.由两角对应相等可得∽,利用对应边成比例可得两岸间的大致距离AB.
9.【答案】B
【解析】解:如图,
,
当王华在CG处时,∽,
即,
当王华在EH处时,∽,
即,
,
米,米,米,米,
设,,
,
解得,
则,
解得,米.
即路灯A的高度米.
故选:B.??
10.【答案】C
【解析】解:
由于是直角三角形,
过P点作直线截,则截得的三角形与有一公共角,
所以只要再作一个直角即可使截得的三角形与相似,
过点P可作AB的垂线、AC的垂线、BC的垂线,共3条直线.
故答案选C.??
11.【答案】
【解析】在中,,,
,,与相似的格点三角形的两直角边长的比为,
在的网格图形中,最长线段的长为,此时与相似的三角形较短的直角边长为4,另一直角边长为8,但画不出端点都在格点上且长为8的线段,故较短直角边长应小于4,在图中尝试,可画出,,的三角形DEF,?,
∽,此时为与相似的面积最大的三角形,其斜边长为.
12.【答案】
【解析】解:如图所示:∽,
,,.
的最长边是.
故答案为.
【答案】?
【解析】?设琪琪制作的三角形框架的最长边长为,
根据题意,得,
解得,
即琪琪制作的三角形框架的最长边长为.
14.【答案】100
【解析】解:,,
∽,
,,
解得:米.
故答案为:100.
15.【答案】∽,
,,.
,,,
,
.
.
16.【答案】解:作法如下.
延长
以点B为圆心,以BC长为半径画弧交CB的延长线于点
连接AD,则即为所求作的三角形,如图所示.
17.【答案】解:四边形EGFH为正方形,
,
∽;
设正方形零件的边长为x?mm,则,,
,
∽,
,
,
,
解得:.
答:正方形零件的边长为48mm.
18.【答案】解:.
理由如下:
平分,
,
::AD,
∽,
,
,
.
19.【答案】解:作线段、、,得即可所求.
证明:、、,
∽,
;
证明:
、E、F分别是三边AB、BC、AC的中点,
,,,
∽,
同理:∽,
由可知:∽,
∽.
第2页,共2页
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
