《第14章位置与坐标》同步能力提升训练(2)2020-2021学年七年级数学青岛版下册(Word版 附答案)
文档属性
| 名称 | 《第14章位置与坐标》同步能力提升训练(2)2020-2021学年七年级数学青岛版下册(Word版 附答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 191.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 00:00:00 | ||
图片预览




文档简介
2021学年青岛版七年级数学下册《第14章位置与坐标》同步能力提升训练2(附答案)
选择题
1.将点A(﹣5,3)向右平移3个单位长度,那么平移后的对应点A′的坐标为( )
A.(﹣5,6)
B.(﹣8,3)
C.(﹣2,3)
D.(﹣5,0)
2.在平面直角坐标系中,有两点坐标分别为(2,0)和(0,3),则这两点之间的距离是( )
A.
B.
C.13
D.5
3.在直角坐标系中,点P(m,2﹣2m)的横坐标与纵坐标互为相反数,则P点在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.下列说法正确的是( )
A.若ab=0,则点P(a,b)表示原点
B.(﹣4)2的算术平方根是4
C.若A(2,﹣2),B(2,2),则直线AB∥x轴
D.负数没有立方根
5.如图,△ABC经过一定的平移得到,如果△ABC上的点P的坐标为(a,b),那么这个点在△A′B′C′上的对应点P′的坐标为( )
A.(a﹣2,b﹣3)
B.(a﹣3,b﹣2)
C.(a+3,b+2)
D.(a+2,b+3)
6.如图是利用平面直角坐标系画出的首钢园中部分场馆建筑的分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示群明湖的点的坐标为(﹣2,0),表示冰壶馆的点的坐标为(﹣3,2),则表示下列场馆建筑的点的坐标正确的是( )
A.滑雪大跳台(﹣5,0)
B.五一剧场(﹣3,﹣2)
C.冬奥组委会(﹣5,4)
D.全民畅读艺术书店(5,0)
7.若点N到x轴的距离是1,到y轴的距离是2,则点N的坐标是( )
A.(1,2)
B.(1,2),(1,﹣2),(﹣1,2),(﹣1,﹣2)
C.(2,1)
D.(2,1),(2,﹣1),(﹣2,1),(﹣2,﹣1)
8.星城长沙是湖南省省会城市,也是长江中游地区重要的中心城市,以下能准确表示长沙地理位置的是( )
A.在北京的西南方
B.东经112.59°,北纬28.12°
C.距离北京1478千米处
D.东经112.59°
9.在平面直角坐标系xOy中,对于点P(x,y),我们把P1(y﹣1,﹣x﹣1)叫做点P的友好点,已知点A1的友好点为A2,点A2的友好点为A3,点A3的友好点为A4,这样依次得到各点.若A2021的坐标为(﹣3,2),设A1(x,y),则x+y的值是( )
A.﹣5
B.3
C.﹣1
D.5
10.如图所示,平面直角坐标系中,x轴负半轴上有一点A(﹣1,0),点A第1次向上平移1个单位至点A1(﹣1,1),接着又向右平移1个单位至点A2(0,1),然后再向上平移1个单位至点A3(0,2),向右平移1个单位至点A4(1,2),…,照此规律平移下去,点A平移至点A2021时,点A2021的坐标是( )
A.(1008,1010)
B.(1009,1010)
C.(1009,1011)
D.(1008,1011)
填空题
11.如图,已知A(2,2),B(﹣4,1),点P在y轴上,当y轴平分∠APB时,线段OP=
.
12.在平面直角坐标系中,已知A(﹣1,﹣1),过点A作x轴的平行线,在该平行线上有一点B.若AB=2,则点B的坐标为
.
13.点A(m﹣1,2m+2)在一、三象限的角平分线上,则m=
.
14.已知点M(﹣3,3),线段MN=4,且MN∥y轴,则点N的坐标是
.
15.在平面直角坐标系内,P到x轴的距离是3,到y轴的距离是5,那么点P的坐标为
.
16.如图,平面直角坐标系中O是原点,等边△OAB的顶点A的坐标是(2,0),动点P从点O出发,以每秒1个单位长度的速度,沿O→A→B→O→A…的路线作循环运动,则第2021秒时,点P的坐标是
.
17.若点P(a+5,2a+1)在第二、四象限角平分线上,则a=
.
18.已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P到x轴、y轴的距离相等.
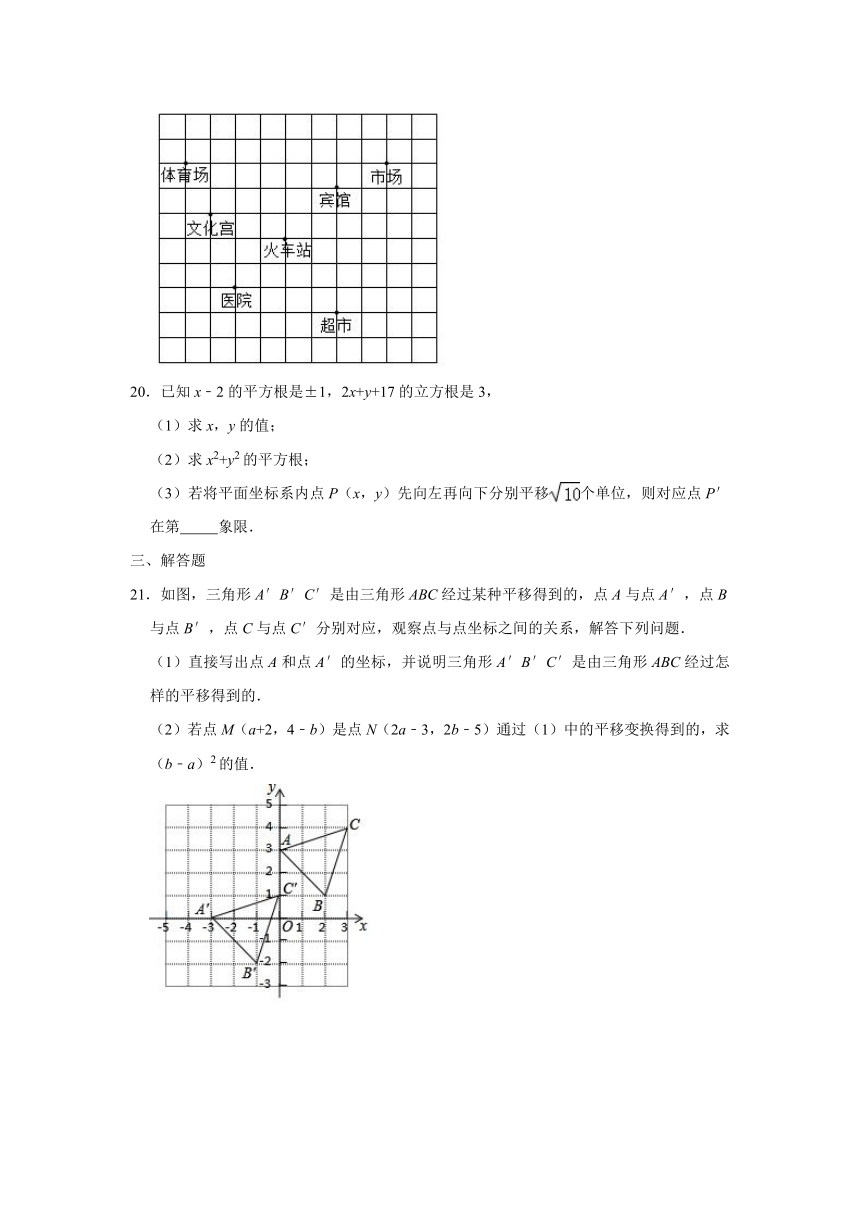
19.如图,这是某市部分建筑分布简图,若火车站的坐标为(﹣1,2),市场的坐标为(3,5),请在图中画出平面直角坐标系,并分别写出超市、体育场和医院的坐标.超市的坐标为
;体育场的坐标为
;医院的坐标为
.
20.已知x﹣2的平方根是±1,2x+y+17的立方根是3,
(1)求x,y的值;
(2)求x2+y2的平方根;
(3)若将平面坐标系内点P(x,y)先向左再向下分别平移个单位,则对应点P′在第
象限.
解答题
21.如图,三角形A′B′C′是由三角形ABC经过某种平移得到的,点A与点A′,点B与点B′,点C与点C′分别对应,观察点与点坐标之间的关系,解答下列问题.
(1)直接写出点A和点A′的坐标,并说明三角形A′B′C′是由三角形ABC经过怎样的平移得到的.
(2)若点M(a+2,4﹣b)是点N(2a﹣3,2b﹣5)通过(1)中的平移变换得到的,求(b﹣a)2的值.
22.在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的三个顶点坐标如表所示:
△ABC
A(a,0)
B(5,3)
C(2,1)
△A′B′C′
A′(3,4)
B′(7,b)
C′(c,d)
(1)观察表中各对应点坐标的变化,并填空:△ABC向右平移
个单位长度,再向上平移
个单位长度可以得到△A′B′C′;a=
,b=
.
(2)求出线段AB在整个平移的过程中在坐标平面上扫过的面积.
(3)若点M(m,n)为线段AB上的一点,则m、n满足的关系式是
.
23.在平面直角坐标系中,分别根据下列条件,求出各点的坐标.
(1)点A在y轴上,位于原点上方,距离原点2个单位长度;
(2)点B在x轴上,位于原点右侧,距离原点1个单位长度;
(3)点C在x轴上方,y轴右侧,距离每条坐标轴都是2个单位长度;
(4)点D在x轴下方,y轴左侧,距离每条坐标轴都是3个单位长度;
(5)点E在x轴下方,y轴右侧,距离x轴2个单位长度,距离y轴4个单位长度.
参考答案
1.解:根据题意,从点A平移到点A′,点A′的纵坐标不变,横坐标是﹣5+3=﹣2,
故点A′的坐标是(﹣2,3).
故选:C.
2.解:∵A(2,0)和B(0,3),
∴OA=2,OB=3,
∴AB=.
故选:C.
3.解:∵点P(m,2﹣2m)的横坐标与纵坐标互为相反数,
∴m+2﹣2m=0,
解得:m=2,
故2﹣2m=2﹣4=﹣2,
则P点坐标为:(2,﹣2),在第四象限.
故选:D.
4.解:A.若ab=0,则a=0,b≠0或b=0,a≠0或a=0,b=0,所以点P(a,b)表示原点或在x轴或y轴上,故A错误,不符合题意;
B.(﹣4)2的算术平方根是4,正确,符合题意;
C.若A(2,﹣2),B(2,2),则直线AB∥y轴,不符合题意;
D.负数有立方根,不符合题意.
故选:B.
5.解:点B的坐标为(﹣2,0),点B′的坐标为(1,2);
横坐标增加了1﹣(﹣2)=3;纵坐标增加了2﹣0=2;
∵△ABC上点P的坐标为(a,b),
∴点P的横坐标为a+3,纵坐标为b+2,
∴点P变换后的对应点P′的坐标为(a+3,b+2),
故选:C.
6.解:滑雪大跳台(﹣5,0),五一剧场(﹣3,4),冬奥组委会(﹣5,8),全民畅读艺术书店(0,5);
故选:A.
7.解:∵点N到x轴的距离是1,到y轴的距离是2,
∴点N的纵坐标为1或﹣1,横坐标为2或﹣2,
∴点N的坐标是(2,1),(2,﹣1),(﹣2,1),(﹣2,﹣1),
故选:D.
8.解:A、在北京的西南方,无法准确确定长沙地理位置;
B、东经112.59°,北纬28.12°,是地球上唯一的点,能准确表示长沙地理位置;
C、距离北京1478千米处,无法准确确定长沙地理位置;
D、东经112.59°,无法准确确定长沙地理位置;
故选:B.
9.解:∵A2021的坐标为(﹣3,2),
根据题意可知:
A2020的坐标为(﹣3,﹣2),
A2019的坐标为(1,﹣2),
A2018的坐标为(1,2),
A2017的坐标为(﹣3,2),
…
∴A4n+1(﹣3,2),A4n+2(1,2),A4n+3(1,﹣2),A4n+4(﹣3,﹣2)(n为自然数).
∵2021=505×4???1,
∵A2021的坐标为(﹣3,2),
∴A1(﹣3,2),
∴x+y=﹣3+2=﹣1.
故选:C.
10.解:由题意,A1(﹣1,1),A3(0,2),A5(1,3),A7(2,4),???,A2n﹣1(﹣2+n,n),
∴A2021(1009,1011),
故选:C.
11.解:如图,当y轴平分∠APB时,点A关于y的对称点A'在BP上,
∵A(2,2),
∴A'(﹣2,2),
设A'B的表达式为y=kx+b,
把A'(﹣2,2),B(﹣4,1)代入,
可得,
解,
∴y=,
令x=0,则y=3,
∴点P的坐标为(0,3),
∴OP=3.故答案为3.
12.解:∵A(﹣1,﹣1),AB∥x轴,AB=2,
∴设B(x,﹣1),
∴|x﹣(﹣1)|=2,
∴x+1=±2,
∴x=1或﹣3,
∴点B的坐标为(1,﹣1)或(﹣3,﹣1).
故答案为(1,﹣1)或(﹣3,﹣1).
13.解:根据题意得m﹣1=2m+2,
解得m=﹣3,
故答案为:﹣3.
14.解:∵线段MN=4,且MN∥y轴,点M(﹣3,3),
∴点N的坐标为(﹣3,y),
∴|y﹣3|=4,
∴y=﹣1或y=7,
∴则点N的坐标是(﹣3,﹣1)或(﹣3,7).
故答案为:(﹣3,﹣1)或(﹣3,7).
15.解:∵点P(x,y)到x轴的距离为3,到y轴的距离为5,
∴点P的横坐标是5或﹣5,纵坐标是3或﹣3,
∴点P的坐标为(﹣5,3),(﹣5,﹣3);(5,3);(5,﹣3).
故答案为:(﹣5,3),(﹣5,﹣3);(5,3);(5,﹣3).
16.解:由题意得,第1秒结束时P点的坐标为P1(1,0);
第2秒结束时P点的坐标为P2(2,0);
第3秒结束时P点的坐标为P3(2﹣1×cos60°,1×sin60°),即P3(,);
第4秒结束时P点的坐标为P4(1,2×sin60°),即P4(1,);
第5秒结束时P点的坐标为P5(,);
第6秒结束时P点的坐标为P6(0,0);
第7秒结束时P点的坐标为P7(1,0),与P1相同;
……
由上可知,P点的坐标按每6秒进行循环,
∵2021÷6=336……5,
∴第2021秒结束后,点P的坐标与P5相同为(,),
故答案为:(,).
17.解:由点P(a+5,2a+1)点在第二、四象限的角平分线上,得
a+5+2a+1=0,
解得a=﹣2,
故答案为:﹣2.
18.解:(1)∵点P(a﹣2,2a+8)在x轴上,
∴2a+8=0,
解得:a=﹣4,
故a﹣2=﹣4﹣2=﹣6,
则P(﹣6,0);
(2)∵点P到x轴、y轴的距离相等,
∴a﹣2=2a+8或a﹣2+2a+8=0,
解得:a1=﹣10,a2=﹣2,
故当a=﹣10时,a﹣2=﹣12,2a+8=﹣12,
则P(﹣12,﹣12);
故当a=﹣2时,a﹣2=﹣4,2a+8=4,
则P(﹣4,4).
综上所述:P(﹣12,﹣12)或(﹣4,4).
19.解:如图所示:超市的坐标为(1,﹣1);
体育场的坐标为(﹣5,5);
医院的坐标为(﹣3,0).
故答案为:(1,﹣1),(﹣5,5),(﹣3,0).
20.解:(1)根据题意知x﹣2=1,2x+y+17=27,
解得x=3,y=4;
(2)∵x=3,y=4,
∴x2+y2=32+42=9+16=25,
则x2+y2的平方根为±5;
(3)由题意知,点P的坐标为(3,4),
平移后点的坐标为(3﹣,4﹣),
∵3﹣<0,4﹣>0,
∴点P的对应点P′在第二象限,
故答案为:二.
21.解:(1)由题意A(0,3),A′(﹣3,0),
三角形A′B′C′是由三角形ABC向左平移3个单位,再向下平移3个单位得到.
(2)由题意,
解得,
∴(b﹣a)2=16.
22.解:(1)∵A(a,0),A′(3,4),
∴△ABC向上平移4个单位后得到△A′B′C′,
∵B(5,3),B′(7,b),
∴△ABC向右平移2个单位后得到△A′B′C′,
∴a=1,b=3+4=7,
故答案为:2;4;1;7;
(2)线段AB在整个平移的过程中在坐标平面上扫过的面积:2×3+4×4=22;
(3)设AB所在直线解析式为y=kx+b,
∵A(1,0),B(5,3),
∴,
解得:,
∴AB所在直线解析式为y=x﹣,
∵点M(m,n)为线段AB上的一点,
∴n=m﹣,
即:3m﹣4n=3,
故答案为:3m﹣4n=3.
23.解:(1)∵点A在y轴上,
∴点A的横坐标为0,
而点A位于原点上方,距离原点2个单位长度,
∴点A的纵坐标为2,
∴点A的坐标为(0,2);
(2)点B在x轴上,
∴点B的纵坐标为0,
而点A位于原点右侧,距离原点1个单位长度,
∴点B的横坐标为﹣1,
∴点B的纵坐标为(1,0);
(3)∵点C在x轴上方,y轴右侧,距离每条坐标轴都是2个单位长度,
∴点C的坐标为(2,2);
(4)∵点D在下轴上方,y轴左侧,距离每条坐标轴都是3个单位长度,
∴点D的坐标为(﹣3,﹣3);
(5)∵点E在x轴下方,y轴右侧,距离x轴2个单位长度,距离y轴4个单位长度,
∴点E的坐标为(4,﹣2).
选择题
1.将点A(﹣5,3)向右平移3个单位长度,那么平移后的对应点A′的坐标为( )
A.(﹣5,6)
B.(﹣8,3)
C.(﹣2,3)
D.(﹣5,0)
2.在平面直角坐标系中,有两点坐标分别为(2,0)和(0,3),则这两点之间的距离是( )
A.
B.
C.13
D.5
3.在直角坐标系中,点P(m,2﹣2m)的横坐标与纵坐标互为相反数,则P点在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.下列说法正确的是( )
A.若ab=0,则点P(a,b)表示原点
B.(﹣4)2的算术平方根是4
C.若A(2,﹣2),B(2,2),则直线AB∥x轴
D.负数没有立方根
5.如图,△ABC经过一定的平移得到,如果△ABC上的点P的坐标为(a,b),那么这个点在△A′B′C′上的对应点P′的坐标为( )
A.(a﹣2,b﹣3)
B.(a﹣3,b﹣2)
C.(a+3,b+2)
D.(a+2,b+3)
6.如图是利用平面直角坐标系画出的首钢园中部分场馆建筑的分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示群明湖的点的坐标为(﹣2,0),表示冰壶馆的点的坐标为(﹣3,2),则表示下列场馆建筑的点的坐标正确的是( )
A.滑雪大跳台(﹣5,0)
B.五一剧场(﹣3,﹣2)
C.冬奥组委会(﹣5,4)
D.全民畅读艺术书店(5,0)
7.若点N到x轴的距离是1,到y轴的距离是2,则点N的坐标是( )
A.(1,2)
B.(1,2),(1,﹣2),(﹣1,2),(﹣1,﹣2)
C.(2,1)
D.(2,1),(2,﹣1),(﹣2,1),(﹣2,﹣1)
8.星城长沙是湖南省省会城市,也是长江中游地区重要的中心城市,以下能准确表示长沙地理位置的是( )
A.在北京的西南方
B.东经112.59°,北纬28.12°
C.距离北京1478千米处
D.东经112.59°
9.在平面直角坐标系xOy中,对于点P(x,y),我们把P1(y﹣1,﹣x﹣1)叫做点P的友好点,已知点A1的友好点为A2,点A2的友好点为A3,点A3的友好点为A4,这样依次得到各点.若A2021的坐标为(﹣3,2),设A1(x,y),则x+y的值是( )
A.﹣5
B.3
C.﹣1
D.5
10.如图所示,平面直角坐标系中,x轴负半轴上有一点A(﹣1,0),点A第1次向上平移1个单位至点A1(﹣1,1),接着又向右平移1个单位至点A2(0,1),然后再向上平移1个单位至点A3(0,2),向右平移1个单位至点A4(1,2),…,照此规律平移下去,点A平移至点A2021时,点A2021的坐标是( )
A.(1008,1010)
B.(1009,1010)
C.(1009,1011)
D.(1008,1011)
填空题
11.如图,已知A(2,2),B(﹣4,1),点P在y轴上,当y轴平分∠APB时,线段OP=
.
12.在平面直角坐标系中,已知A(﹣1,﹣1),过点A作x轴的平行线,在该平行线上有一点B.若AB=2,则点B的坐标为
.
13.点A(m﹣1,2m+2)在一、三象限的角平分线上,则m=
.
14.已知点M(﹣3,3),线段MN=4,且MN∥y轴,则点N的坐标是
.
15.在平面直角坐标系内,P到x轴的距离是3,到y轴的距离是5,那么点P的坐标为
.
16.如图,平面直角坐标系中O是原点,等边△OAB的顶点A的坐标是(2,0),动点P从点O出发,以每秒1个单位长度的速度,沿O→A→B→O→A…的路线作循环运动,则第2021秒时,点P的坐标是
.
17.若点P(a+5,2a+1)在第二、四象限角平分线上,则a=
.
18.已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P到x轴、y轴的距离相等.
19.如图,这是某市部分建筑分布简图,若火车站的坐标为(﹣1,2),市场的坐标为(3,5),请在图中画出平面直角坐标系,并分别写出超市、体育场和医院的坐标.超市的坐标为
;体育场的坐标为
;医院的坐标为
.
20.已知x﹣2的平方根是±1,2x+y+17的立方根是3,
(1)求x,y的值;
(2)求x2+y2的平方根;
(3)若将平面坐标系内点P(x,y)先向左再向下分别平移个单位,则对应点P′在第
象限.
解答题
21.如图,三角形A′B′C′是由三角形ABC经过某种平移得到的,点A与点A′,点B与点B′,点C与点C′分别对应,观察点与点坐标之间的关系,解答下列问题.
(1)直接写出点A和点A′的坐标,并说明三角形A′B′C′是由三角形ABC经过怎样的平移得到的.
(2)若点M(a+2,4﹣b)是点N(2a﹣3,2b﹣5)通过(1)中的平移变换得到的,求(b﹣a)2的值.
22.在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的三个顶点坐标如表所示:
△ABC
A(a,0)
B(5,3)
C(2,1)
△A′B′C′
A′(3,4)
B′(7,b)
C′(c,d)
(1)观察表中各对应点坐标的变化,并填空:△ABC向右平移
个单位长度,再向上平移
个单位长度可以得到△A′B′C′;a=
,b=
.
(2)求出线段AB在整个平移的过程中在坐标平面上扫过的面积.
(3)若点M(m,n)为线段AB上的一点,则m、n满足的关系式是
.
23.在平面直角坐标系中,分别根据下列条件,求出各点的坐标.
(1)点A在y轴上,位于原点上方,距离原点2个单位长度;
(2)点B在x轴上,位于原点右侧,距离原点1个单位长度;
(3)点C在x轴上方,y轴右侧,距离每条坐标轴都是2个单位长度;
(4)点D在x轴下方,y轴左侧,距离每条坐标轴都是3个单位长度;
(5)点E在x轴下方,y轴右侧,距离x轴2个单位长度,距离y轴4个单位长度.
参考答案
1.解:根据题意,从点A平移到点A′,点A′的纵坐标不变,横坐标是﹣5+3=﹣2,
故点A′的坐标是(﹣2,3).
故选:C.
2.解:∵A(2,0)和B(0,3),
∴OA=2,OB=3,
∴AB=.
故选:C.
3.解:∵点P(m,2﹣2m)的横坐标与纵坐标互为相反数,
∴m+2﹣2m=0,
解得:m=2,
故2﹣2m=2﹣4=﹣2,
则P点坐标为:(2,﹣2),在第四象限.
故选:D.
4.解:A.若ab=0,则a=0,b≠0或b=0,a≠0或a=0,b=0,所以点P(a,b)表示原点或在x轴或y轴上,故A错误,不符合题意;
B.(﹣4)2的算术平方根是4,正确,符合题意;
C.若A(2,﹣2),B(2,2),则直线AB∥y轴,不符合题意;
D.负数有立方根,不符合题意.
故选:B.
5.解:点B的坐标为(﹣2,0),点B′的坐标为(1,2);
横坐标增加了1﹣(﹣2)=3;纵坐标增加了2﹣0=2;
∵△ABC上点P的坐标为(a,b),
∴点P的横坐标为a+3,纵坐标为b+2,
∴点P变换后的对应点P′的坐标为(a+3,b+2),
故选:C.
6.解:滑雪大跳台(﹣5,0),五一剧场(﹣3,4),冬奥组委会(﹣5,8),全民畅读艺术书店(0,5);
故选:A.
7.解:∵点N到x轴的距离是1,到y轴的距离是2,
∴点N的纵坐标为1或﹣1,横坐标为2或﹣2,
∴点N的坐标是(2,1),(2,﹣1),(﹣2,1),(﹣2,﹣1),
故选:D.
8.解:A、在北京的西南方,无法准确确定长沙地理位置;
B、东经112.59°,北纬28.12°,是地球上唯一的点,能准确表示长沙地理位置;
C、距离北京1478千米处,无法准确确定长沙地理位置;
D、东经112.59°,无法准确确定长沙地理位置;
故选:B.
9.解:∵A2021的坐标为(﹣3,2),
根据题意可知:
A2020的坐标为(﹣3,﹣2),
A2019的坐标为(1,﹣2),
A2018的坐标为(1,2),
A2017的坐标为(﹣3,2),
…
∴A4n+1(﹣3,2),A4n+2(1,2),A4n+3(1,﹣2),A4n+4(﹣3,﹣2)(n为自然数).
∵2021=505×4???1,
∵A2021的坐标为(﹣3,2),
∴A1(﹣3,2),
∴x+y=﹣3+2=﹣1.
故选:C.
10.解:由题意,A1(﹣1,1),A3(0,2),A5(1,3),A7(2,4),???,A2n﹣1(﹣2+n,n),
∴A2021(1009,1011),
故选:C.
11.解:如图,当y轴平分∠APB时,点A关于y的对称点A'在BP上,
∵A(2,2),
∴A'(﹣2,2),
设A'B的表达式为y=kx+b,
把A'(﹣2,2),B(﹣4,1)代入,
可得,
解,
∴y=,
令x=0,则y=3,
∴点P的坐标为(0,3),
∴OP=3.故答案为3.
12.解:∵A(﹣1,﹣1),AB∥x轴,AB=2,
∴设B(x,﹣1),
∴|x﹣(﹣1)|=2,
∴x+1=±2,
∴x=1或﹣3,
∴点B的坐标为(1,﹣1)或(﹣3,﹣1).
故答案为(1,﹣1)或(﹣3,﹣1).
13.解:根据题意得m﹣1=2m+2,
解得m=﹣3,
故答案为:﹣3.
14.解:∵线段MN=4,且MN∥y轴,点M(﹣3,3),
∴点N的坐标为(﹣3,y),
∴|y﹣3|=4,
∴y=﹣1或y=7,
∴则点N的坐标是(﹣3,﹣1)或(﹣3,7).
故答案为:(﹣3,﹣1)或(﹣3,7).
15.解:∵点P(x,y)到x轴的距离为3,到y轴的距离为5,
∴点P的横坐标是5或﹣5,纵坐标是3或﹣3,
∴点P的坐标为(﹣5,3),(﹣5,﹣3);(5,3);(5,﹣3).
故答案为:(﹣5,3),(﹣5,﹣3);(5,3);(5,﹣3).
16.解:由题意得,第1秒结束时P点的坐标为P1(1,0);
第2秒结束时P点的坐标为P2(2,0);
第3秒结束时P点的坐标为P3(2﹣1×cos60°,1×sin60°),即P3(,);
第4秒结束时P点的坐标为P4(1,2×sin60°),即P4(1,);
第5秒结束时P点的坐标为P5(,);
第6秒结束时P点的坐标为P6(0,0);
第7秒结束时P点的坐标为P7(1,0),与P1相同;
……
由上可知,P点的坐标按每6秒进行循环,
∵2021÷6=336……5,
∴第2021秒结束后,点P的坐标与P5相同为(,),
故答案为:(,).
17.解:由点P(a+5,2a+1)点在第二、四象限的角平分线上,得
a+5+2a+1=0,
解得a=﹣2,
故答案为:﹣2.
18.解:(1)∵点P(a﹣2,2a+8)在x轴上,
∴2a+8=0,
解得:a=﹣4,
故a﹣2=﹣4﹣2=﹣6,
则P(﹣6,0);
(2)∵点P到x轴、y轴的距离相等,
∴a﹣2=2a+8或a﹣2+2a+8=0,
解得:a1=﹣10,a2=﹣2,
故当a=﹣10时,a﹣2=﹣12,2a+8=﹣12,
则P(﹣12,﹣12);
故当a=﹣2时,a﹣2=﹣4,2a+8=4,
则P(﹣4,4).
综上所述:P(﹣12,﹣12)或(﹣4,4).
19.解:如图所示:超市的坐标为(1,﹣1);
体育场的坐标为(﹣5,5);
医院的坐标为(﹣3,0).
故答案为:(1,﹣1),(﹣5,5),(﹣3,0).
20.解:(1)根据题意知x﹣2=1,2x+y+17=27,
解得x=3,y=4;
(2)∵x=3,y=4,
∴x2+y2=32+42=9+16=25,
则x2+y2的平方根为±5;
(3)由题意知,点P的坐标为(3,4),
平移后点的坐标为(3﹣,4﹣),
∵3﹣<0,4﹣>0,
∴点P的对应点P′在第二象限,
故答案为:二.
21.解:(1)由题意A(0,3),A′(﹣3,0),
三角形A′B′C′是由三角形ABC向左平移3个单位,再向下平移3个单位得到.
(2)由题意,
解得,
∴(b﹣a)2=16.
22.解:(1)∵A(a,0),A′(3,4),
∴△ABC向上平移4个单位后得到△A′B′C′,
∵B(5,3),B′(7,b),
∴△ABC向右平移2个单位后得到△A′B′C′,
∴a=1,b=3+4=7,
故答案为:2;4;1;7;
(2)线段AB在整个平移的过程中在坐标平面上扫过的面积:2×3+4×4=22;
(3)设AB所在直线解析式为y=kx+b,
∵A(1,0),B(5,3),
∴,
解得:,
∴AB所在直线解析式为y=x﹣,
∵点M(m,n)为线段AB上的一点,
∴n=m﹣,
即:3m﹣4n=3,
故答案为:3m﹣4n=3.
23.解:(1)∵点A在y轴上,
∴点A的横坐标为0,
而点A位于原点上方,距离原点2个单位长度,
∴点A的纵坐标为2,
∴点A的坐标为(0,2);
(2)点B在x轴上,
∴点B的纵坐标为0,
而点A位于原点右侧,距离原点1个单位长度,
∴点B的横坐标为﹣1,
∴点B的纵坐标为(1,0);
(3)∵点C在x轴上方,y轴右侧,距离每条坐标轴都是2个单位长度,
∴点C的坐标为(2,2);
(4)∵点D在下轴上方,y轴左侧,距离每条坐标轴都是3个单位长度,
∴点D的坐标为(﹣3,﹣3);
(5)∵点E在x轴下方,y轴右侧,距离x轴2个单位长度,距离y轴4个单位长度,
∴点E的坐标为(4,﹣2).
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
