2020-2021学年青岛版七年级数学下册《第13章 平面图形的认识》同步提升训练(Word版 附答案)
文档属性
| 名称 | 2020-2021学年青岛版七年级数学下册《第13章 平面图形的认识》同步提升训练(Word版 附答案) |  | |
| 格式 | doc | ||
| 文件大小 | 227.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 12:45:00 | ||
图片预览




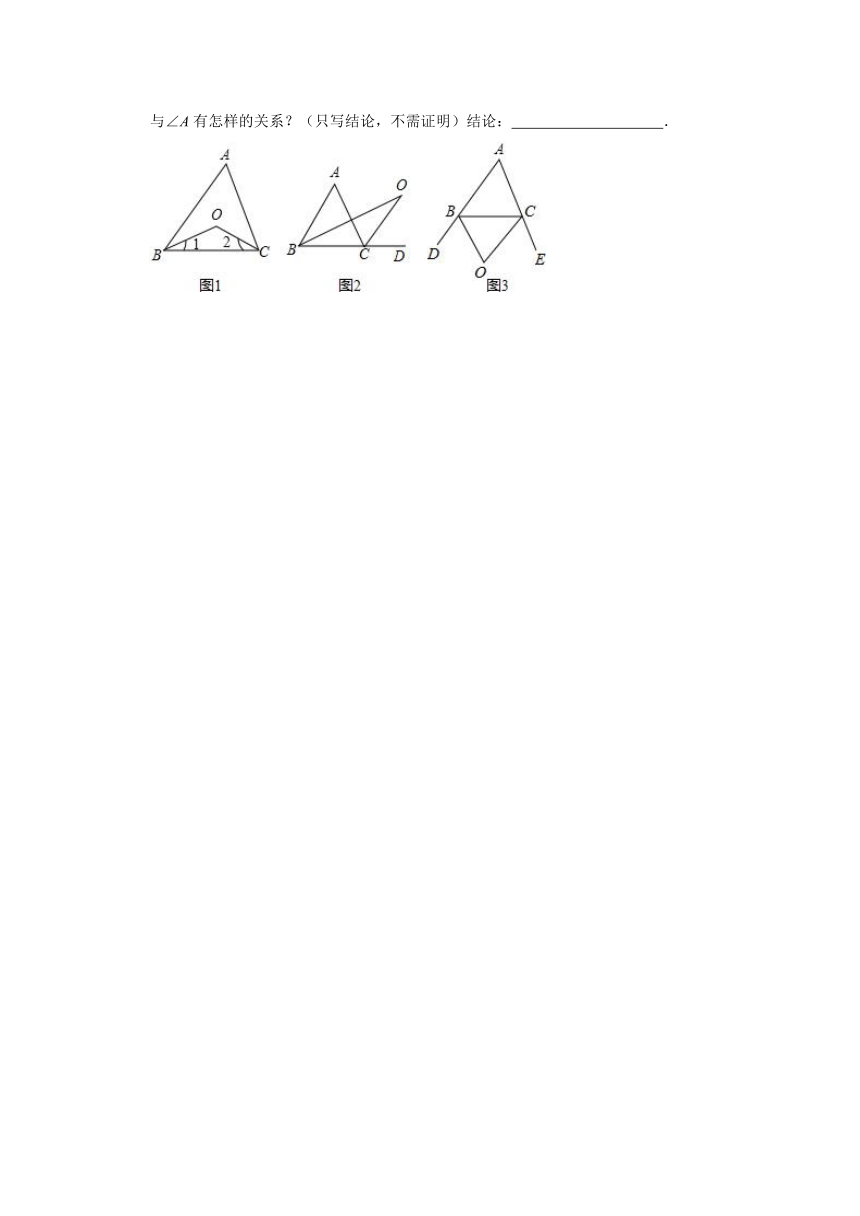
文档简介
2021年青岛版七年级数学下册《第13章平面图形的认识》同步提升训练(附答案)
选择题
1.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有( )
A.2对
B.3对
C.4对
D.6对
2.如图,在△ABC中,AD、BF、CE相交于O点,则图中的三角形的个数是( )
A.7个
B.10个
C.15个
D.16个
3.如图,△ABC中,边BC=12cm,高AD=6cm,边长为x的正方形PQMN的一边在BC上,其余两个顶点分别在AB、AC上,则正方形边长x为( )
A.3cm
B.4cm
C.5cm
D.6cm
4.如图,长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,若点C也在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C个数( )
A.2
B.3
C.4
D.5
5.在△ABC中,AD是BC边上的中线,G是重心.如果AG=6,那么线段DG的长为( )
A.2
B.3
C.6
D.12
6.在直角△ABC中,∠C=90°,CB=6,CA=8,G为重心,到斜边AB的距离为( )
A.
B.
C.
D.2
7.现有3cm,4cm,7cm,9cm长的四根木棒,任取其中三根组成一个三角形,那么可以组成的三角形的个数是( )
A.1个
B.2个
C.3个
D.4个
8.课题学习时,老师布置画一个三角形ABC,使∠A=30°,AB=10cm,∠A的对边BC可以在长为4cm、5cm、6cm、11cm四条线段中任选,这样最多可以画( )个互不全等的三角形.
A.3个
B.4个
C.5个
D.6个
9.如图,∠A=35°,∠B=∠C=90°,则∠D的度数是( )
A.35°
B.45°
C.55°
D.65°
10.如图,AB∥CD,EF⊥AB于E,EF交CD于F,已知∠2=30°,则∠1是( )
A.20°
B.60°
C.30°
D.45°
填空题
11.某同学在纸上画了四个点,如果把这四个点彼此连接,连成一个图形,则这个图形中会有
个三角形出现.
12.如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是
.
13.如图,G是△ABC的重心,AG⊥GC,AC=4,则BG的长为
.
14.三条整数长度的线段不能构成三角形的总长度和的最小值为1+2+3=6,四条整数长度的线段任意三条均不能构成三角形的总长度和的最小值为1+2+3+5=11,由此请探究:一根钢管长2009cm,现把此钢管截成整数长的小钢管,使任意三根钢管均不能围成三角形,这根钢管最多可以截成
根整数长的小钢管.
15.如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=36°,则∠CAP=
.
解答题
16.两条平行直线上各有n个点,用这n对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当n=1时的情况,此时图中三角形的个数为0;
图2展示了当n=2时的一种情况,此时图中三角形的个数为2;
(1)当n=3时,在图3中画出使三角形个数最少的图形,此时图中三角形的个数为
个;
(2)试猜想当n对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当n=2021时,按上述规则画出的图形中,最少有多少个三角形?
17.如图,学校有一块三角形空地(即△ABC),现准备将它分成面积相等的两块地,栽种不同的花草,请你把它分出来.(作图题要求:尺规作图,保留作图痕迹,不写作法,不要求证明).
18.如图,在四边形ABCD中,对角线AC与BD相交于P,请添加一个条件,使四边形ABCD的面积为:S四边形ABCD=AC?BD,并说明理由.
19.如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,AE平分∠DAC,∠B=50°,求∠BAD和∠AEC的度数.
20.认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线
∴
∴
又∵∠ABC+∠ACB=180°﹣∠A
∴
∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣∠A)=
探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)结论:
.
参考答案
1.解:△BDC与△BEC、△BDC与△BAC、△BEC与△BAC共三对.
故选:B.
2.解:6+3+6+1=16个三角形.故选D.
3.解:设正方形的边长为x,PN交AD于E,如右图,连接PD、DN.
(BD+CD)x+AD(PE+NE)=,
解得x=4.
故选:B.
4.解:C点所有的情况如图所示:
故选:C.
5.解:∵三角形的重心到顶点的距离是其到对边中点的距离的2倍,
∴DG=AG=3.
故选:B.
6.解:设CD是Rt△ABC的斜边上的中线,三角形的重心G在线段CD上,过点G作GE⊥AB于点E,过点C作CE⊥AB于点F,
∵在△ABC中,∠ACB=90°,AC=8,BC=6,
∴AB==10,
如图,CD是Rt△ABC的斜边上的中线,
∴三角形的重心G在线段CD上,
∴DG=CD,
∵GE∥CF,
∴EG=FC,
∵FC×AB=AC×BC,
∴FC=,
∴GE=×=,
即△ABC的重心到斜边AB的距离为:.
故选:A.
7.解:四条木棒的所有组合:3,4,7和3,4,9和3,7,9和4,7,9;
只有3,7,9和4,7,9能组成三角形.
故选:B.
8.解:如图,过B作BD⊥直线AC于D,
则线段BD的长度是B到直线AC的最短距离,
∵∠A=30°,AB=10cm,
∴BD=AB=5cm,而垂线段最短,
∴在长为4cm、5cm、6cm、11cm四条线段中有5cm、11cm可以各画1个互不全等的三角形,6cm可以画二个互不全等的三角形.
故选:B.
9.解:∵∠B=∠C=90°,∠AOB=∠COD,
∴∠D=∠A=35°.
故选:A.
10.解:∵AB∥CD,EF⊥AB,
∴EF⊥CD.
∵∠2=30°,
∴∠1=∠3=90°﹣∠2=60°.
故选:B.
11.解:∵①当四个点共线时,不能作出三角形;
②当三个点共线,第四个点不在这条直线上时,能够画出3个三角形;
③若4个点能构成凹四边形,则能画出4个三角形;
④当任意的三个点不共线时,则能够画出8个三角形.
∴0或3或4或8.
12.方法1
解:∵△ABC的三条中线AD、BE,CF交于点G,
∴S△CGE=S△AGE=S△ACF,S△BGF=S△BGD=S△BCF,
∵S△ACF=S△BCF=S△ABC=×12=6,
∴S△CGE=S△ACF=×6=2,S△BGF=S△BCF=×6=2,
∴S阴影=S△CGE+S△BGF=4.
故答案为4.
方法2
设△AFG,△BFG,△BDG,△CDG,△CEG,△AEG的面积分别为S1,S2,S3,S4,S5,S6,根据中线平分三角形面积可得:S1=S2,S3=S4,S5=S6,S1+S2+S3=S4+S5+S6①,S2+S3+S4=S1+S5+S6②
由①﹣②可得S1=S4,所以S1=S2=S3=S4=S5=S6=2,故阴影部分的面积为4.
故答案为:4.
13.解:延长BG交AC于D点,
∵G是△ABC的重心,
∴BD为△ABC的中线;
又∵AG⊥GC,
∴GD为Rt△AGC斜边上的中线,
∴GD=AC,
∵G是△ABC的重心,
∴BG=2GD=AC=4.
14.解:1+2+3+5+8+13+21+34+55+89+144+233+377+610=1595.
所以把此钢管截成整数长的小钢管,使任意三根钢管均不能围成三角形,这根钢管最多可以截成14根整数长的小钢管.
故答案为14.
15.解:过P点作PF⊥BA于F,PN⊥BD于N,PM⊥AC于M,
设∠PCD=x°,
∵CP平分∠ACD,
∴∠ACP=∠PCD=x°,PM=PN,
∵BP平分∠ABC,
∴∠ABP=∠PBC,PF=PN,
∴PF=PM,
又∵PF⊥BA于F,PM⊥AC于M,
∴∠FAP=∠PAC.
∵∠BPC=36°,
∴∠ABP=∠PBC=(x﹣36)°,
∴∠BAC=∠ACD﹣∠ABC=2x°﹣(x°﹣36°)﹣(x°﹣36°)=72°,
∴∠CAF=108°,
∴∠FAP=∠PAC=54°.
故答案为:54°.
16.解:(1)
4个;
(2)当有n对点时,最少可以画2(n﹣1)个三角形;
(3)2×(2021﹣1)=4041个.
答:当n=2021时,最少可以画4041个三角形.
17.解:作图如下:
.
18.解:条件:AC⊥BD,理由:
∵AC⊥BD,
∴,,
∴S四边形ABCD=S△ACD+S△ACB
=+
=
=.
19.解:在△ABC中,
∵∠BAC=90°,∠B=50°,
∴∠C=90°﹣∠B=40°,
∵AD⊥BC于点D,
∴∠BAD=90°﹣∠B=40°;
在△ADC中,
∵∠ADC=90°,∠C=40°,
∴∠DAC=90°﹣∠C=50°,
∵AE平分∠DAC,
∴∠DAE=∠DAC=25°,
在△DAE中,
∵∠ADE=90°,∠DAE=25°,
∴∠AED=90°﹣∠DAE=65°,
∴∠AEC=180°﹣∠AED=180°﹣65°=115°.
20.解:(1)探究2结论:∠BOC=∠A,
理由如下:
∵BO和CO分别是∠ABC和∠ACD的角平分线,
∴∠1=∠ABC,∠2=∠ACD,
又∵∠ACD是△ABC的一外角,
∴∠ACD=∠A+∠ABC,
∴∠2=(∠A+∠ABC)=∠A+∠1,
∵∠2是△BOC的一外角,
∴∠BOC=∠2﹣∠1=∠A+∠1﹣∠1=∠A;
(2)探究3:∠OBC=(∠A+∠ACB),∠OCB=(∠A+∠ABC),
∠BOC=180°﹣∠0BC﹣∠OCB,
=180°﹣(∠A+∠ACB)﹣(∠A+∠ABC),
=180°﹣∠A﹣(∠A+∠ABC+∠ACB),
结论∠BOC=90°﹣∠A.
选择题
1.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有( )
A.2对
B.3对
C.4对
D.6对
2.如图,在△ABC中,AD、BF、CE相交于O点,则图中的三角形的个数是( )
A.7个
B.10个
C.15个
D.16个
3.如图,△ABC中,边BC=12cm,高AD=6cm,边长为x的正方形PQMN的一边在BC上,其余两个顶点分别在AB、AC上,则正方形边长x为( )
A.3cm
B.4cm
C.5cm
D.6cm
4.如图,长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,若点C也在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C个数( )
A.2
B.3
C.4
D.5
5.在△ABC中,AD是BC边上的中线,G是重心.如果AG=6,那么线段DG的长为( )
A.2
B.3
C.6
D.12
6.在直角△ABC中,∠C=90°,CB=6,CA=8,G为重心,到斜边AB的距离为( )
A.
B.
C.
D.2
7.现有3cm,4cm,7cm,9cm长的四根木棒,任取其中三根组成一个三角形,那么可以组成的三角形的个数是( )
A.1个
B.2个
C.3个
D.4个
8.课题学习时,老师布置画一个三角形ABC,使∠A=30°,AB=10cm,∠A的对边BC可以在长为4cm、5cm、6cm、11cm四条线段中任选,这样最多可以画( )个互不全等的三角形.
A.3个
B.4个
C.5个
D.6个
9.如图,∠A=35°,∠B=∠C=90°,则∠D的度数是( )
A.35°
B.45°
C.55°
D.65°
10.如图,AB∥CD,EF⊥AB于E,EF交CD于F,已知∠2=30°,则∠1是( )
A.20°
B.60°
C.30°
D.45°
填空题
11.某同学在纸上画了四个点,如果把这四个点彼此连接,连成一个图形,则这个图形中会有
个三角形出现.
12.如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是
.
13.如图,G是△ABC的重心,AG⊥GC,AC=4,则BG的长为
.
14.三条整数长度的线段不能构成三角形的总长度和的最小值为1+2+3=6,四条整数长度的线段任意三条均不能构成三角形的总长度和的最小值为1+2+3+5=11,由此请探究:一根钢管长2009cm,现把此钢管截成整数长的小钢管,使任意三根钢管均不能围成三角形,这根钢管最多可以截成
根整数长的小钢管.
15.如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=36°,则∠CAP=
.
解答题
16.两条平行直线上各有n个点,用这n对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当n=1时的情况,此时图中三角形的个数为0;
图2展示了当n=2时的一种情况,此时图中三角形的个数为2;
(1)当n=3时,在图3中画出使三角形个数最少的图形,此时图中三角形的个数为
个;
(2)试猜想当n对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当n=2021时,按上述规则画出的图形中,最少有多少个三角形?
17.如图,学校有一块三角形空地(即△ABC),现准备将它分成面积相等的两块地,栽种不同的花草,请你把它分出来.(作图题要求:尺规作图,保留作图痕迹,不写作法,不要求证明).
18.如图,在四边形ABCD中,对角线AC与BD相交于P,请添加一个条件,使四边形ABCD的面积为:S四边形ABCD=AC?BD,并说明理由.
19.如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,AE平分∠DAC,∠B=50°,求∠BAD和∠AEC的度数.
20.认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线
∴
∴
又∵∠ABC+∠ACB=180°﹣∠A
∴
∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣∠A)=
探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)结论:
.
参考答案
1.解:△BDC与△BEC、△BDC与△BAC、△BEC与△BAC共三对.
故选:B.
2.解:6+3+6+1=16个三角形.故选D.
3.解:设正方形的边长为x,PN交AD于E,如右图,连接PD、DN.
(BD+CD)x+AD(PE+NE)=,
解得x=4.
故选:B.
4.解:C点所有的情况如图所示:
故选:C.
5.解:∵三角形的重心到顶点的距离是其到对边中点的距离的2倍,
∴DG=AG=3.
故选:B.
6.解:设CD是Rt△ABC的斜边上的中线,三角形的重心G在线段CD上,过点G作GE⊥AB于点E,过点C作CE⊥AB于点F,
∵在△ABC中,∠ACB=90°,AC=8,BC=6,
∴AB==10,
如图,CD是Rt△ABC的斜边上的中线,
∴三角形的重心G在线段CD上,
∴DG=CD,
∵GE∥CF,
∴EG=FC,
∵FC×AB=AC×BC,
∴FC=,
∴GE=×=,
即△ABC的重心到斜边AB的距离为:.
故选:A.
7.解:四条木棒的所有组合:3,4,7和3,4,9和3,7,9和4,7,9;
只有3,7,9和4,7,9能组成三角形.
故选:B.
8.解:如图,过B作BD⊥直线AC于D,
则线段BD的长度是B到直线AC的最短距离,
∵∠A=30°,AB=10cm,
∴BD=AB=5cm,而垂线段最短,
∴在长为4cm、5cm、6cm、11cm四条线段中有5cm、11cm可以各画1个互不全等的三角形,6cm可以画二个互不全等的三角形.
故选:B.
9.解:∵∠B=∠C=90°,∠AOB=∠COD,
∴∠D=∠A=35°.
故选:A.
10.解:∵AB∥CD,EF⊥AB,
∴EF⊥CD.
∵∠2=30°,
∴∠1=∠3=90°﹣∠2=60°.
故选:B.
11.解:∵①当四个点共线时,不能作出三角形;
②当三个点共线,第四个点不在这条直线上时,能够画出3个三角形;
③若4个点能构成凹四边形,则能画出4个三角形;
④当任意的三个点不共线时,则能够画出8个三角形.
∴0或3或4或8.
12.方法1
解:∵△ABC的三条中线AD、BE,CF交于点G,
∴S△CGE=S△AGE=S△ACF,S△BGF=S△BGD=S△BCF,
∵S△ACF=S△BCF=S△ABC=×12=6,
∴S△CGE=S△ACF=×6=2,S△BGF=S△BCF=×6=2,
∴S阴影=S△CGE+S△BGF=4.
故答案为4.
方法2
设△AFG,△BFG,△BDG,△CDG,△CEG,△AEG的面积分别为S1,S2,S3,S4,S5,S6,根据中线平分三角形面积可得:S1=S2,S3=S4,S5=S6,S1+S2+S3=S4+S5+S6①,S2+S3+S4=S1+S5+S6②
由①﹣②可得S1=S4,所以S1=S2=S3=S4=S5=S6=2,故阴影部分的面积为4.
故答案为:4.
13.解:延长BG交AC于D点,
∵G是△ABC的重心,
∴BD为△ABC的中线;
又∵AG⊥GC,
∴GD为Rt△AGC斜边上的中线,
∴GD=AC,
∵G是△ABC的重心,
∴BG=2GD=AC=4.
14.解:1+2+3+5+8+13+21+34+55+89+144+233+377+610=1595.
所以把此钢管截成整数长的小钢管,使任意三根钢管均不能围成三角形,这根钢管最多可以截成14根整数长的小钢管.
故答案为14.
15.解:过P点作PF⊥BA于F,PN⊥BD于N,PM⊥AC于M,
设∠PCD=x°,
∵CP平分∠ACD,
∴∠ACP=∠PCD=x°,PM=PN,
∵BP平分∠ABC,
∴∠ABP=∠PBC,PF=PN,
∴PF=PM,
又∵PF⊥BA于F,PM⊥AC于M,
∴∠FAP=∠PAC.
∵∠BPC=36°,
∴∠ABP=∠PBC=(x﹣36)°,
∴∠BAC=∠ACD﹣∠ABC=2x°﹣(x°﹣36°)﹣(x°﹣36°)=72°,
∴∠CAF=108°,
∴∠FAP=∠PAC=54°.
故答案为:54°.
16.解:(1)
4个;
(2)当有n对点时,最少可以画2(n﹣1)个三角形;
(3)2×(2021﹣1)=4041个.
答:当n=2021时,最少可以画4041个三角形.
17.解:作图如下:
.
18.解:条件:AC⊥BD,理由:
∵AC⊥BD,
∴,,
∴S四边形ABCD=S△ACD+S△ACB
=+
=
=.
19.解:在△ABC中,
∵∠BAC=90°,∠B=50°,
∴∠C=90°﹣∠B=40°,
∵AD⊥BC于点D,
∴∠BAD=90°﹣∠B=40°;
在△ADC中,
∵∠ADC=90°,∠C=40°,
∴∠DAC=90°﹣∠C=50°,
∵AE平分∠DAC,
∴∠DAE=∠DAC=25°,
在△DAE中,
∵∠ADE=90°,∠DAE=25°,
∴∠AED=90°﹣∠DAE=65°,
∴∠AEC=180°﹣∠AED=180°﹣65°=115°.
20.解:(1)探究2结论:∠BOC=∠A,
理由如下:
∵BO和CO分别是∠ABC和∠ACD的角平分线,
∴∠1=∠ABC,∠2=∠ACD,
又∵∠ACD是△ABC的一外角,
∴∠ACD=∠A+∠ABC,
∴∠2=(∠A+∠ABC)=∠A+∠1,
∵∠2是△BOC的一外角,
∴∠BOC=∠2﹣∠1=∠A+∠1﹣∠1=∠A;
(2)探究3:∠OBC=(∠A+∠ACB),∠OCB=(∠A+∠ABC),
∠BOC=180°﹣∠0BC﹣∠OCB,
=180°﹣(∠A+∠ACB)﹣(∠A+∠ABC),
=180°﹣∠A﹣(∠A+∠ABC+∠ACB),
结论∠BOC=90°﹣∠A.
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
