《3.4 相似三角形的判定与性质》课时同步练习2020-2021学年数学湘教版九年级上册(Word版 含答案)
文档属性
| 名称 | 《3.4 相似三角形的判定与性质》课时同步练习2020-2021学年数学湘教版九年级上册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 302.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 13:06:54 | ||
图片预览



文档简介
《3.4
相似三角形的判定与性质》课时同步练习2020-2021年数学湘教版九(上)
一.选择题(共10小题)
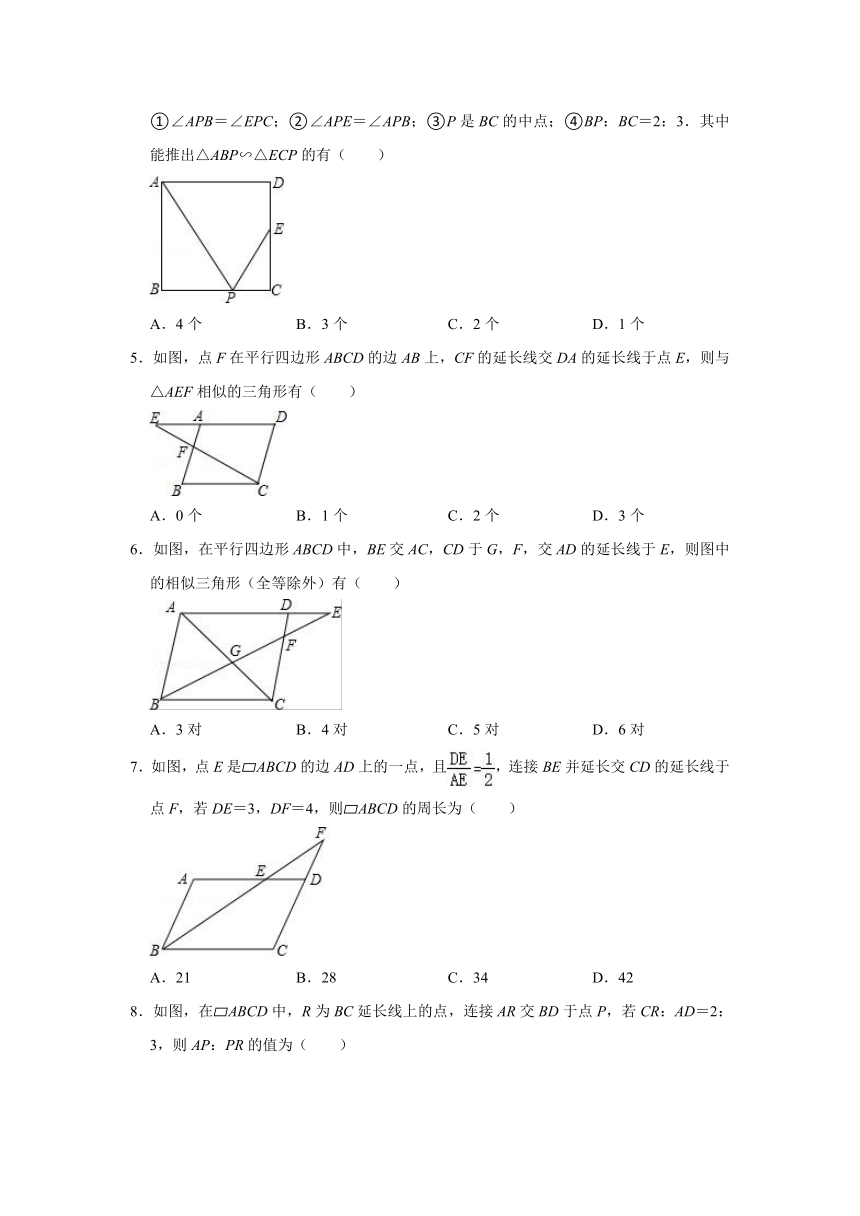
1.如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A.
B.
C.
D.
2.如图,已知矩形ABCD中,点E是边AD上的任一点,连接BE,过E作BE的垂线交BC延长线于点F,交边CD于点P,则图中共有相似三角形( )
A.6对
B.5对
C.4对
D.3对
3.如图,下列条件不能判定△ABC与△ADE相似的是( )
A.=
B.∠B=∠ADE
C.=
D.∠C=∠AED
4.如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:
①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中点;④BP:BC=2:3.其中能推出△ABP∽△ECP的有( )
A.4个
B.3个
C.2个
D.1个
5.如图,点F在平行四边形ABCD的边AB上,CF的延长线交DA的延长线于点E,则与△AEF相似的三角形有( )
A.0个
B.1个
C.2个
D.3个
6.如图,在平行四边形ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形(全等除外)有( )
A.3对
B.4对
C.5对
D.6对
7.如图,点E是?ABCD的边AD上的一点,且,连接BE并延长交CD的延长线于点F,若DE=3,DF=4,则?ABCD的周长为( )
A.21
B.28
C.34
D.42
8.如图,在?ABCD中,R为BC延长线上的点,连接AR交BD于点P,若CR:AD=2:3,则AP:PR的值为( )
A.3:5
B.2:3
C.3:4
D.3:2
9.如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为( )
A.18
B.
C.
D.
10.已知△ABC∽△DEF,S△ABC:S△DEF=9,且△ABC的周长为18,则△DEF的周长为( )
A.2
B.3
C.6
D.54
二.填空题(共6小题)
11.在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,当AE=
时,以A、D、E为顶点的三角形与△ABC相似.
12.如图,∠1=∠2,添加一个条件使得△ADE∽△ACB,可添加的条件是
.
13.如图,在矩形ABCD中,AB=2,BC=4,E是CD延长线上一点,连接BE交AD于点F,连接CF,若△ABF与△CEF的面积相等,则DE的长为
.
14.如图,已知AD:DB=2:1,CE:EA=2:3,则CF:DF=
.
15.两三角形的相似比为1:4,它们的周长之差为27
cm,则较小三角形的周长为
.
16.若△ABC∽△DEF,且对应高线的比为2:3,则它们的面积比为
.
三.解答题(共8小题)
17.如图,已知在△ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DB?CE.求证:△ADB∽△EAC.
18.在△ABC中,∠BAC=90°,AB=AC,点D是BC边上一点,过点D作∠ADE=45°,DE交AC于点E,求证:△ABD∽△DCE.
19.如图,已知正方形ABCD,点E在CB延长线上,点F在BC延长线上,连接DE、DF、EF交AB于点G,若AG=CF,求证:CD2=CE?CF.
20.如图,已知正方形ABCD的边长为4,F为BC上一点,且BF=3,E为DC上的点.
(1)若∠AEF=90°,求证:△ADE∽△ECF;
(2)若△ADE与△ECF相似,求CE的长.
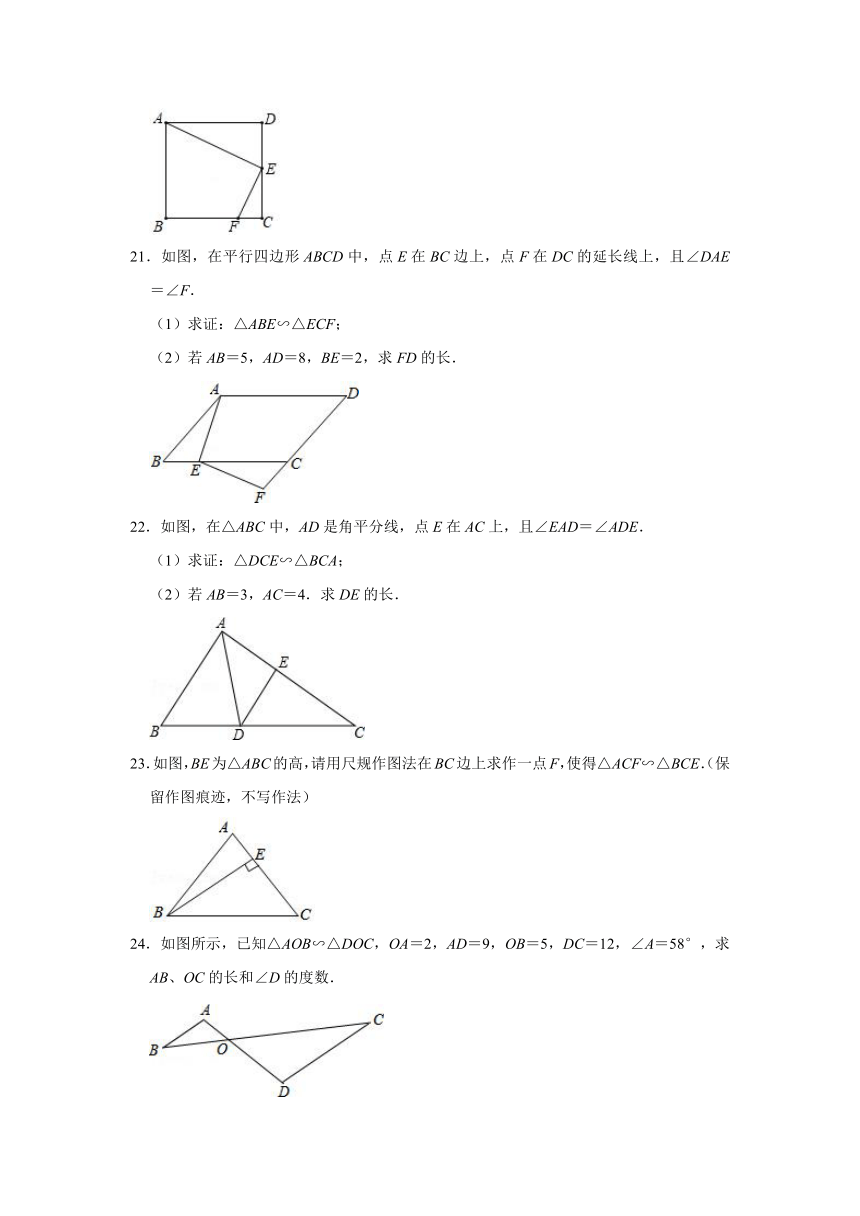
21.如图,在平行四边形ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
(1)求证:△ABE∽△ECF;
(2)若AB=5,AD=8,BE=2,求FD的长.
22.如图,在△ABC中,AD是角平分线,点E在AC上,且∠EAD=∠ADE.
(1)求证:△DCE∽△BCA;
(2)若AB=3,AC=4.求DE的长.
23.如图,BE为△ABC的高,请用尺规作图法在BC边上求作一点F,使得△ACF∽△BCE.(保留作图痕迹,不写作法)
24.如图所示,已知△AOB∽△DOC,OA=2,AD=9,OB=5,DC=12,∠A=58°,求AB、OC的长和∠D的度数.
参考答案
一.选择题(共10小题)
1.解:A、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项错误;
B、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项错误;
C、两三角形的对应边不成比例,故两三角形不相似,故本选项正确.
D、两三角形对应边成比例且夹角相等,故两三角形相似,故本选项错误;
故选:C.
2.解:∵四边形ABCD是矩形,
∴∠A=∠ABC=∠D=∠DCB=90°,
∴∠PCF=90°,
∵BE⊥EF,
∴∠BEF=90°,
∴∠ABE+∠AEB=∠AEB+∠DEP=90°,
∴∠ABE=∠DEP,
∵AD∥BC,
∴∠DEP=∠F,
∴∠ABE=∠DEP=∠F,
∴△ABE∽△DEP∽△EFB∽△CFP,
∴图中共有相似三角形有6对,
故选:A.
3.解:(B)∵∠A=∠A,
∠B=∠ADE,
∴△ABC∽△ADE,故B可以判断,
(C)∵
∠A=∠A
∴△ABC∽△ADE,故C可以判断,
(D)∵∠A=∠A,
∠C=∠AED,
∴△ABC∽△ADE,故D可以判断,
故选:A.
4.解:∵四边形ABCD为正方形,
∴AB=BC=CD,∠B=∠C=90°,
∵E为CD中点,
∴CD=2CE,即AB=BC=2CE,
①当∠APB=∠EPC时,结合∠B=∠C,可推出△ABP∽△ECP;
②当∠APE=∠APB≠60°时,则有∠APB≠∠EPC,所以不能推出△ABP∽△ECP;
③当P是BC中点时,则有BC=2PC,可知PC=CE,则△PCE为等腰直角三角形,而BP≠AB,即△ABP不是等腰直角三角形,故不能推出△ABP∽△ECP;
④当BP:BC=2:3时,则有BP:PC=2:1,且AB:CE=2:1,结合∠B=∠C,可推出△ABP∽△ECP相似;
故选:C.
5.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
由AF∥CD,可以推出△EAF∽△EDC,
由AE∥BC,可以推出△AEF∽△BCF,
故选:C.
6.解:∵AD∥BC,
∴△AGE∽△CGB,△DFE∽△CFB,
∵AB∥CD,
∴△ABG∽△CFG,△ABE∽△CFB,△EDF∽△EAB.
∴共有5对,
故选:C.
7.解:∵四边形ABCD是平行四边形,
∴AB∥CF,AB=CD,
∴△ABE∽△DFE,
∴,
∵DE=3,DF=4,
∴AE=6,AB=8,
∴AD=AE+DE=6+3=9,
∴平行四边形ABCD的周长为:(8+9)×2=34.
故选:C.
8.解:∵在?ABCD中,AD∥BC,且AD=BC,
∴△ADP∽△RBP,
∴,
∴.
∵CR:AD=2:3,
∴CR=AD,
∴=.
故选:A.
9.解:∵四边形ABCD是正方形,AB=12,BM=5,
∴MC=12﹣5=7.
∵ME⊥AM,
∴∠AME=90°,
∴∠AMB+∠CMG=90°.
∵∠AMB+∠BAM=90°,
∴∠BAM=∠CMG,∠B=∠C=90°,
∴△ABM∽△MCG,
∴=,即=,解得CG=,
∴DG=12﹣=.
∵AE∥BC,
∴∠E=CMG,∠EDG=∠C,
∴△MCG∽△EDG,
∴=,即=,解得DE=.
故选:B.
10.解:∵△ABC∽△DEF,S△ABC:S△DEF=9,
∴△ABC与△DEF的相似比为:3:1,
∴△ABC与△DEF的周长比为:3:1,
∵△ABC的周长为18厘米,
∴,
∴△DEF的周长为6厘米.
故选:C.
二.填空题(共6小题)
11.解:当=时,
∵∠A=∠A,
∴△AED∽△ABC,
此时AE===;
当=时,
∵∠A=∠A,
∴△ADE∽△ABC,
此时AE===;
故答案为:或.
12.解:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,即∠DAE=∠BAC.
当∠D=∠B或∠E=∠C或时,△ADE∽△ACB.
故答案为:∠D=∠B或∠E=∠C或
13.解:设DE=x.
∵DF∥BC,
∴△EFD∽△EBC,
∴,
∴,
∴DF=,AF=4﹣=,
∵△ABF与△CEF的面积相等,
∴?AF?AB=?EC?DF,
∴×2=×(x+2),
∴x1=﹣1,x2=﹣﹣1(舍去),
故答案为:﹣1.
14.解:过D作DM∥AC,交BE于M,
∵DM∥AC,
∴△BMD∽△BEA,
∴=,
∵AD:DB=2:1,
∴===,
即AE=3DM,
∵CE:EA=2:3,
∴CE=2DM,
∵DM∥AC,
∴△DMF∽△CEF,
∴===,
故答案为:2:1.
15.解:令较大的三角形的周长为xcm.
小三角形的周长为(x﹣27)cm,
由两个相似三角形对应中线的比为1:4得,
1:4=(x﹣27):x,
解之得x=36cm,
x﹣27=36﹣27=9cm.
故答案为9cm.
16.解:∵△ABC∽△DEF,对应高线的比为2:3,
∴它们的相似比为2:3,
∴它们的面积比为()2=.
故答案为:.
三.解答题(共8小题)
17.证明:∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABD=∠ACE,
∵AB2=DB?CE,
,
∴,
∴,
∴△ADB∽△EAC.
18.证明:如图所示:
∵∠BAC=90°,AB=AC,
∴△ABC为等腰直角三角形,
∴∠B=∠C=45°,
∴∠1+∠2=180°﹣∠B=135°,
∵∠ADE=45°,
∴∠2+∠3=135°,
∴∠1=∠3,
∵∠B=∠C,
∴△ABD∽△DCE.
19.证明:∵四边形ABCD为正方形,
∴AD=CD,∠A=∠ECD=∠DCF=90°.
在△ADG和△CDF中,,
∴△ADG≌△CDF(SAS),
∴∠ADG=∠CDF.
∵AD∥BE,
∴∠ADG=∠E,
∴∠E=∠CDF.
又∵∠ECD=∠DCF=90°,
∴△ECD∽△DCF,
∴=,
即CD2=CE?CF.
20.(1)证明:∵正方形ABCD,
∴∠D=∠C=90°,
∴∠AED+∠DAE=90°,
∵∠AEF=90°,
∴∠AED+∠CEF=90°,
∴∠DAE=∠CEF,
∴△ADE∽△ECF.
(2)∵正方形ABCD的边长为4,F为BC上一点,BF=3,E为DC上的点,
∴CF=1,DE=4﹣CE,
分两种情况:
①∵△ADE∽△ECF,
∴=.
∴=.
解得CE=2.
②∵△ADE∽△FCE,
∴=.
∴=.
解得CE=.
∴CE的长是2或.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠B=∠ECF,∠DAE=∠AEB.
又∵∠DAE=∠F,
∴∠AEB=∠F.
∴△ABE∽△ECF;
(2)解:∵△ABE∽△ECF,
∴=,
∵四边形ABCD是平行四边形,
∴BC=AD=8.CD=AB=5,
∴EC=BC﹣BE=8﹣2=6.
∴=.
∴CF=,
∴FD=CD+CF=
22.(1)证明:∵AD平分∠BAC,
∴∠BAD=∠EDA,
∵∠EAD=∠ADE,
∴∠BAD=∠ADE,
∴AB∥DE,
∴△DCE∽△BCA;
(2)解:∵∠EAD=∠ADE,
∴AE=DE,
设DE=x,
∴CE=AC﹣AE=AC﹣DE=4﹣x,
∵△DCE∽△BCA,
∴DE:AB=CE:AC,
即x:3=(4﹣x):4,
解得:x=,
∴DE的长是.
23.解:如图,△ACF即为所求.
24.解:∵OA=2,AD=9,
∴OD=9﹣2=7,
∵AB∥CD,
∴△AOB∽△DOC,
∴==,
∵OA=2,OB=5,DC=12,
∴==,
解得OC=,AB=,
∵△AOB∽△DOC,
∴∠D=∠A=58°.
相似三角形的判定与性质》课时同步练习2020-2021年数学湘教版九(上)
一.选择题(共10小题)
1.如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A.
B.
C.
D.
2.如图,已知矩形ABCD中,点E是边AD上的任一点,连接BE,过E作BE的垂线交BC延长线于点F,交边CD于点P,则图中共有相似三角形( )
A.6对
B.5对
C.4对
D.3对
3.如图,下列条件不能判定△ABC与△ADE相似的是( )
A.=
B.∠B=∠ADE
C.=
D.∠C=∠AED
4.如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:
①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中点;④BP:BC=2:3.其中能推出△ABP∽△ECP的有( )
A.4个
B.3个
C.2个
D.1个
5.如图,点F在平行四边形ABCD的边AB上,CF的延长线交DA的延长线于点E,则与△AEF相似的三角形有( )
A.0个
B.1个
C.2个
D.3个
6.如图,在平行四边形ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形(全等除外)有( )
A.3对
B.4对
C.5对
D.6对
7.如图,点E是?ABCD的边AD上的一点,且,连接BE并延长交CD的延长线于点F,若DE=3,DF=4,则?ABCD的周长为( )
A.21
B.28
C.34
D.42
8.如图,在?ABCD中,R为BC延长线上的点,连接AR交BD于点P,若CR:AD=2:3,则AP:PR的值为( )
A.3:5
B.2:3
C.3:4
D.3:2
9.如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为( )
A.18
B.
C.
D.
10.已知△ABC∽△DEF,S△ABC:S△DEF=9,且△ABC的周长为18,则△DEF的周长为( )
A.2
B.3
C.6
D.54
二.填空题(共6小题)
11.在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,当AE=
时,以A、D、E为顶点的三角形与△ABC相似.
12.如图,∠1=∠2,添加一个条件使得△ADE∽△ACB,可添加的条件是
.
13.如图,在矩形ABCD中,AB=2,BC=4,E是CD延长线上一点,连接BE交AD于点F,连接CF,若△ABF与△CEF的面积相等,则DE的长为
.
14.如图,已知AD:DB=2:1,CE:EA=2:3,则CF:DF=
.
15.两三角形的相似比为1:4,它们的周长之差为27
cm,则较小三角形的周长为
.
16.若△ABC∽△DEF,且对应高线的比为2:3,则它们的面积比为
.
三.解答题(共8小题)
17.如图,已知在△ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DB?CE.求证:△ADB∽△EAC.
18.在△ABC中,∠BAC=90°,AB=AC,点D是BC边上一点,过点D作∠ADE=45°,DE交AC于点E,求证:△ABD∽△DCE.
19.如图,已知正方形ABCD,点E在CB延长线上,点F在BC延长线上,连接DE、DF、EF交AB于点G,若AG=CF,求证:CD2=CE?CF.
20.如图,已知正方形ABCD的边长为4,F为BC上一点,且BF=3,E为DC上的点.
(1)若∠AEF=90°,求证:△ADE∽△ECF;
(2)若△ADE与△ECF相似,求CE的长.
21.如图,在平行四边形ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
(1)求证:△ABE∽△ECF;
(2)若AB=5,AD=8,BE=2,求FD的长.
22.如图,在△ABC中,AD是角平分线,点E在AC上,且∠EAD=∠ADE.
(1)求证:△DCE∽△BCA;
(2)若AB=3,AC=4.求DE的长.
23.如图,BE为△ABC的高,请用尺规作图法在BC边上求作一点F,使得△ACF∽△BCE.(保留作图痕迹,不写作法)
24.如图所示,已知△AOB∽△DOC,OA=2,AD=9,OB=5,DC=12,∠A=58°,求AB、OC的长和∠D的度数.
参考答案
一.选择题(共10小题)
1.解:A、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项错误;
B、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项错误;
C、两三角形的对应边不成比例,故两三角形不相似,故本选项正确.
D、两三角形对应边成比例且夹角相等,故两三角形相似,故本选项错误;
故选:C.
2.解:∵四边形ABCD是矩形,
∴∠A=∠ABC=∠D=∠DCB=90°,
∴∠PCF=90°,
∵BE⊥EF,
∴∠BEF=90°,
∴∠ABE+∠AEB=∠AEB+∠DEP=90°,
∴∠ABE=∠DEP,
∵AD∥BC,
∴∠DEP=∠F,
∴∠ABE=∠DEP=∠F,
∴△ABE∽△DEP∽△EFB∽△CFP,
∴图中共有相似三角形有6对,
故选:A.
3.解:(B)∵∠A=∠A,
∠B=∠ADE,
∴△ABC∽△ADE,故B可以判断,
(C)∵
∠A=∠A
∴△ABC∽△ADE,故C可以判断,
(D)∵∠A=∠A,
∠C=∠AED,
∴△ABC∽△ADE,故D可以判断,
故选:A.
4.解:∵四边形ABCD为正方形,
∴AB=BC=CD,∠B=∠C=90°,
∵E为CD中点,
∴CD=2CE,即AB=BC=2CE,
①当∠APB=∠EPC时,结合∠B=∠C,可推出△ABP∽△ECP;
②当∠APE=∠APB≠60°时,则有∠APB≠∠EPC,所以不能推出△ABP∽△ECP;
③当P是BC中点时,则有BC=2PC,可知PC=CE,则△PCE为等腰直角三角形,而BP≠AB,即△ABP不是等腰直角三角形,故不能推出△ABP∽△ECP;
④当BP:BC=2:3时,则有BP:PC=2:1,且AB:CE=2:1,结合∠B=∠C,可推出△ABP∽△ECP相似;
故选:C.
5.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
由AF∥CD,可以推出△EAF∽△EDC,
由AE∥BC,可以推出△AEF∽△BCF,
故选:C.
6.解:∵AD∥BC,
∴△AGE∽△CGB,△DFE∽△CFB,
∵AB∥CD,
∴△ABG∽△CFG,△ABE∽△CFB,△EDF∽△EAB.
∴共有5对,
故选:C.
7.解:∵四边形ABCD是平行四边形,
∴AB∥CF,AB=CD,
∴△ABE∽△DFE,
∴,
∵DE=3,DF=4,
∴AE=6,AB=8,
∴AD=AE+DE=6+3=9,
∴平行四边形ABCD的周长为:(8+9)×2=34.
故选:C.
8.解:∵在?ABCD中,AD∥BC,且AD=BC,
∴△ADP∽△RBP,
∴,
∴.
∵CR:AD=2:3,
∴CR=AD,
∴=.
故选:A.
9.解:∵四边形ABCD是正方形,AB=12,BM=5,
∴MC=12﹣5=7.
∵ME⊥AM,
∴∠AME=90°,
∴∠AMB+∠CMG=90°.
∵∠AMB+∠BAM=90°,
∴∠BAM=∠CMG,∠B=∠C=90°,
∴△ABM∽△MCG,
∴=,即=,解得CG=,
∴DG=12﹣=.
∵AE∥BC,
∴∠E=CMG,∠EDG=∠C,
∴△MCG∽△EDG,
∴=,即=,解得DE=.
故选:B.
10.解:∵△ABC∽△DEF,S△ABC:S△DEF=9,
∴△ABC与△DEF的相似比为:3:1,
∴△ABC与△DEF的周长比为:3:1,
∵△ABC的周长为18厘米,
∴,
∴△DEF的周长为6厘米.
故选:C.
二.填空题(共6小题)
11.解:当=时,
∵∠A=∠A,
∴△AED∽△ABC,
此时AE===;
当=时,
∵∠A=∠A,
∴△ADE∽△ABC,
此时AE===;
故答案为:或.
12.解:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,即∠DAE=∠BAC.
当∠D=∠B或∠E=∠C或时,△ADE∽△ACB.
故答案为:∠D=∠B或∠E=∠C或
13.解:设DE=x.
∵DF∥BC,
∴△EFD∽△EBC,
∴,
∴,
∴DF=,AF=4﹣=,
∵△ABF与△CEF的面积相等,
∴?AF?AB=?EC?DF,
∴×2=×(x+2),
∴x1=﹣1,x2=﹣﹣1(舍去),
故答案为:﹣1.
14.解:过D作DM∥AC,交BE于M,
∵DM∥AC,
∴△BMD∽△BEA,
∴=,
∵AD:DB=2:1,
∴===,
即AE=3DM,
∵CE:EA=2:3,
∴CE=2DM,
∵DM∥AC,
∴△DMF∽△CEF,
∴===,
故答案为:2:1.
15.解:令较大的三角形的周长为xcm.
小三角形的周长为(x﹣27)cm,
由两个相似三角形对应中线的比为1:4得,
1:4=(x﹣27):x,
解之得x=36cm,
x﹣27=36﹣27=9cm.
故答案为9cm.
16.解:∵△ABC∽△DEF,对应高线的比为2:3,
∴它们的相似比为2:3,
∴它们的面积比为()2=.
故答案为:.
三.解答题(共8小题)
17.证明:∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABD=∠ACE,
∵AB2=DB?CE,
,
∴,
∴,
∴△ADB∽△EAC.
18.证明:如图所示:
∵∠BAC=90°,AB=AC,
∴△ABC为等腰直角三角形,
∴∠B=∠C=45°,
∴∠1+∠2=180°﹣∠B=135°,
∵∠ADE=45°,
∴∠2+∠3=135°,
∴∠1=∠3,
∵∠B=∠C,
∴△ABD∽△DCE.
19.证明:∵四边形ABCD为正方形,
∴AD=CD,∠A=∠ECD=∠DCF=90°.
在△ADG和△CDF中,,
∴△ADG≌△CDF(SAS),
∴∠ADG=∠CDF.
∵AD∥BE,
∴∠ADG=∠E,
∴∠E=∠CDF.
又∵∠ECD=∠DCF=90°,
∴△ECD∽△DCF,
∴=,
即CD2=CE?CF.
20.(1)证明:∵正方形ABCD,
∴∠D=∠C=90°,
∴∠AED+∠DAE=90°,
∵∠AEF=90°,
∴∠AED+∠CEF=90°,
∴∠DAE=∠CEF,
∴△ADE∽△ECF.
(2)∵正方形ABCD的边长为4,F为BC上一点,BF=3,E为DC上的点,
∴CF=1,DE=4﹣CE,
分两种情况:
①∵△ADE∽△ECF,
∴=.
∴=.
解得CE=2.
②∵△ADE∽△FCE,
∴=.
∴=.
解得CE=.
∴CE的长是2或.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠B=∠ECF,∠DAE=∠AEB.
又∵∠DAE=∠F,
∴∠AEB=∠F.
∴△ABE∽△ECF;
(2)解:∵△ABE∽△ECF,
∴=,
∵四边形ABCD是平行四边形,
∴BC=AD=8.CD=AB=5,
∴EC=BC﹣BE=8﹣2=6.
∴=.
∴CF=,
∴FD=CD+CF=
22.(1)证明:∵AD平分∠BAC,
∴∠BAD=∠EDA,
∵∠EAD=∠ADE,
∴∠BAD=∠ADE,
∴AB∥DE,
∴△DCE∽△BCA;
(2)解:∵∠EAD=∠ADE,
∴AE=DE,
设DE=x,
∴CE=AC﹣AE=AC﹣DE=4﹣x,
∵△DCE∽△BCA,
∴DE:AB=CE:AC,
即x:3=(4﹣x):4,
解得:x=,
∴DE的长是.
23.解:如图,△ACF即为所求.
24.解:∵OA=2,AD=9,
∴OD=9﹣2=7,
∵AB∥CD,
∴△AOB∽△DOC,
∴==,
∵OA=2,OB=5,DC=12,
∴==,
解得OC=,AB=,
∵△AOB∽△DOC,
∴∠D=∠A=58°.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
