九年级数学相似三角形的性质
图片预览




文档简介
(共25张PPT)
24.3.3相似三角形的性质
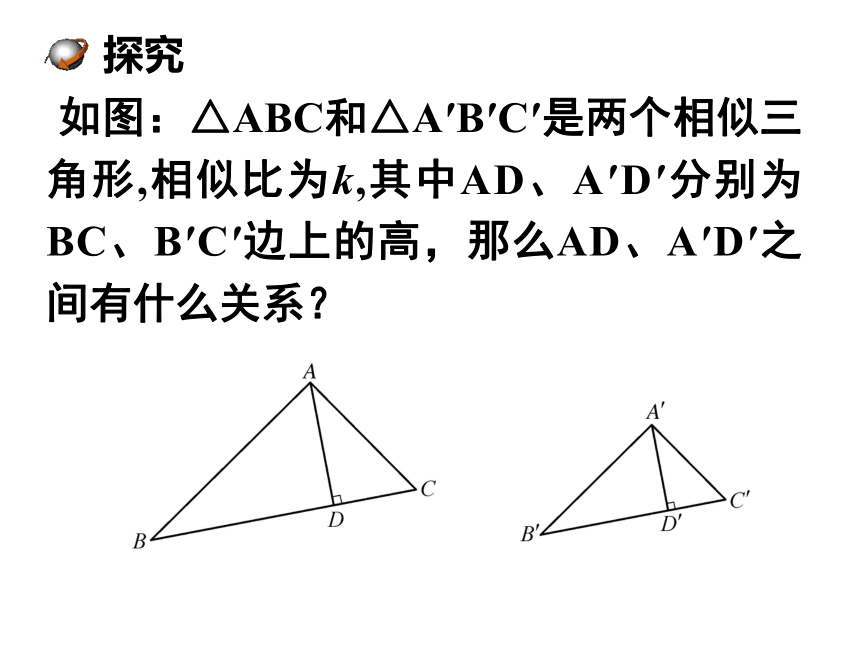
如图:△ABC和△A′B′C′是两个相似三角形,相似比为k,其中AD、A′D′分别为BC、B′C′边上的高,那么AD、A′D′之间有什么关系?
探究
∴
A’
B’
D’
C’
B
C
D
A
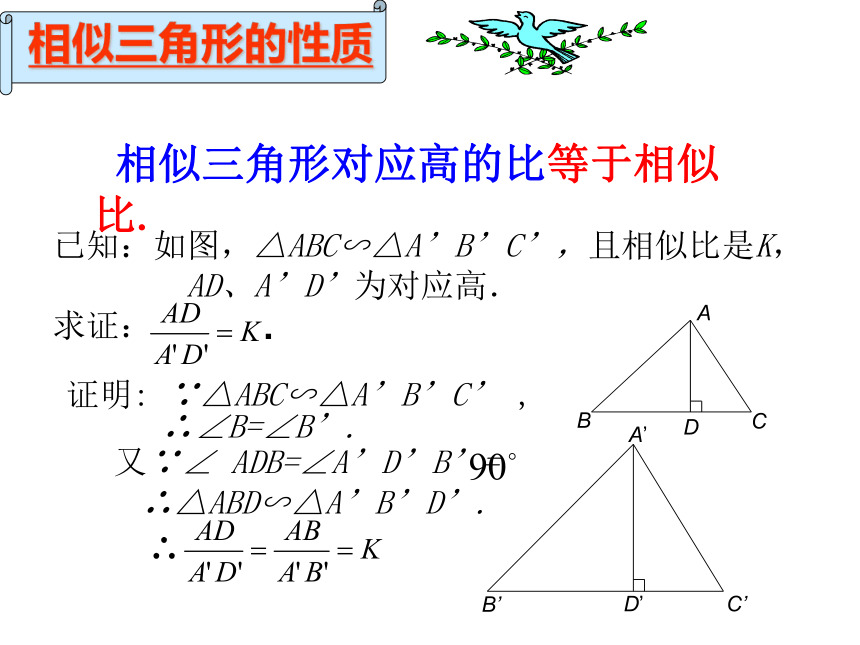
相似三角形对应高的比等于相似比.
证明: ∵△ABC∽△A’B’C’ ,
∴∠B=∠B’.
又∵∠ ADB=∠A’D’B’=
∴△ABD∽△A’B’D’.
相似三角形的性质
已知:如图,△ABC∽△A’B’C’,且相似比是K,
AD、A’D’为对应高.
求证:
.
思考:如图,△ABC和△A′B′C′相似,AD、A′D′分别为对应边上的中线,BE、B′E′分别为对应角的角平分线,那么它们之间有什么关系呢?
相似三角形的对应中线的比等于相似比.
相似三角形的对应角平分线的比等于相似比.
理论
相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.
性质1
相似三角形的性质
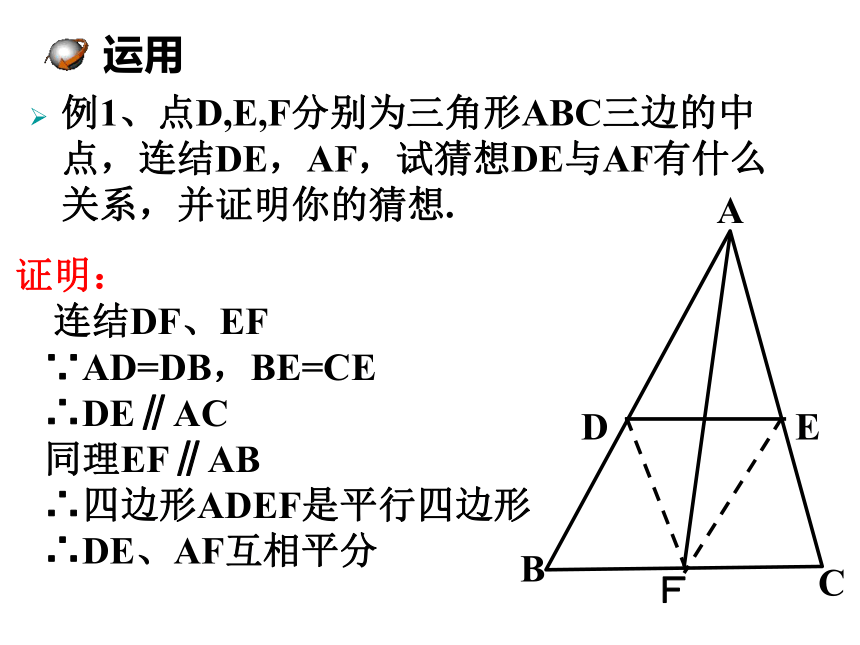
例1、点D,E,F分别为三角形ABC三边的中点,连结DE,AF,试猜想DE与AF有什么关系,并证明你的猜想.
A
B
C
D
E
F
证明:
连结DF、EF
∵AD=DB,BE=CE
∴DE∥AC
同理EF∥AB
∴四边形ADEF是平行四边形
∴DE、AF互相平分
运用
A
B
C
D
E
F
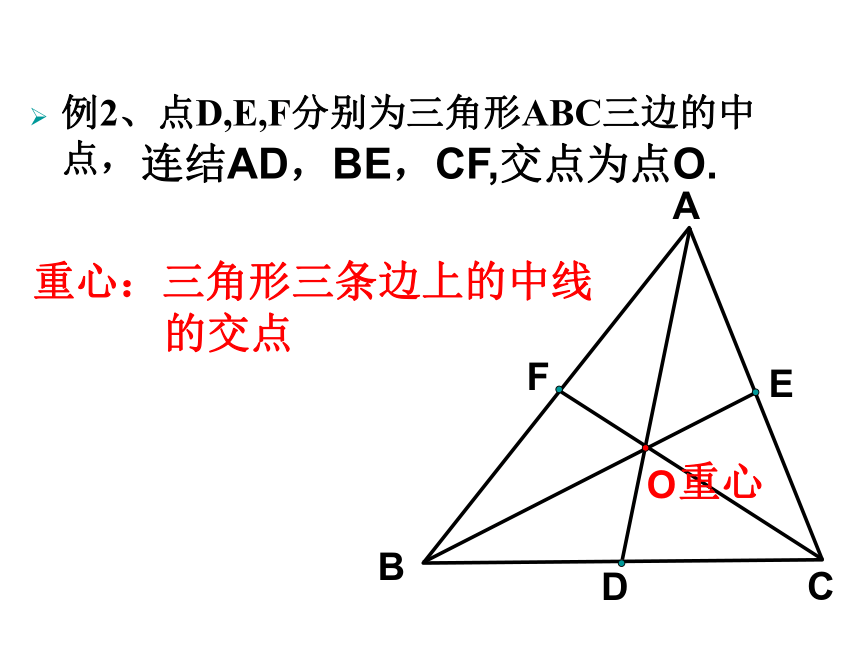
例2、点D,E,F分别为三角形ABC三边的中点,
O
重心
重心:三角形三条边上的中线
的交点
连结AD,BE,CF,交点为点O.
运用
结论1:三角形的重心与一边中点的连线
的长是对应中线长的三分之一
A
B
C
D
E
F
O
例4. 如图,点O为三角形ABC的重心,
猜想△AOB、 △ AOC、 △ BOC的
面积有怎样的关系?说明理由.
A
B
C
D
E
F
O
P
Q
结论2:三角形的重心与三角形三个顶点
组成的三个三角形的面积相等.
A
B
C
D
E
F
O
从而由等比性质有
相似三角形周长的比等于
相似比.
性质2
相似三角形的性质
性质证明
图中(1)、(2)、(3)分别是边长为1、2、3的等边三角形,它们都相似.
(2)与(1)的相似比=__________,
(2)与(1)的面积比=__________;
(3)与(1)的相似比=__________,
(3)与(1)的面积比=__________.
2:1
4:1
3:1
9:1
探究
已知:△ABC∽△A′B′C′,且相似比为k,AD、 A′D′分别是△ABC、△A′B′C′对应边BC、 B′C′上的高.
求证: .
证明:
∴
∴
∵ △ABC∽△A′B′C′,
性质3:相似三角形的面积比等于相似比的平方.
1.相似三角形对应边的比为0.4,那么相似比为______,对应角的角平分线的比为______,周长的比为______,面积的比为______.
2:5
2:5
2:5
4:25
演练
2. 已知△ABC∽△A’B’C’,且A’C’=3, BC=5,
AC=4,AB=7,则△A’B’C’的周长是 .
12
3. 已知△ABC∽△A’B’C’,
S△ABC:S△A’B’C’ =9:25, △ ABC的周长
是36,则△ ABC的周长是 .
60
4. 如图,在△ABC中,点D,E分别在AB,AC上,DE平行于BC,AD:DB=3:2,求四边形DBCE与△ADE的面积比.
解:∵DE∥BC
∴∠ADE=∠B ∠AED=∠C
∴△ADE∽△ABC
S△ADE:S△ABC=(AD:AB)2
∵AD:DB=3:2
∴AD:AB=3:5
∴S△ADE:S△ABC=9:25
∴S△ADE:S四边形DBCE=9:16
所以四边形DBCE与△ADE的面积比为16:9
5.如图,△ABC的边BC=12cm,高AD=6cm,边长为x
的正方形PQMN的一边在BC上,其余两个顶点
分别在AB、AC上.
(1)求x的值;
(2)求△APN与 △ABC
的面积比
B
Q
D
M
C
A
P
N
E
6. 如图,在梯形ABCD中,AB∥CD,
AC,BD相交于点E, S△DEC:S△CEB =1:2,
则S△DEC:S△BEA 等于 .
A
D
C
B
E
1:4
O
A1
A2
A3
A4
A
B
B1
B2
B3
1
4
7.如图,点
在射线
上,点
在射线
上,且
,
若
、
的面积分别为1,4,
则图中三个阴影三角形面积之和为 .
O
A1
A2
A3
A4
A
B
B1
B2
B3
1
4
10.5
课堂小结:
今天我们学习相似三角形哪些性质?
1、相似三角形对应高的比等于相似比,
相似三角形对应中线的比等于相似比,
相似三角形对应角平分线的比等于相似比。
2、相似三角形周长的比等于相似比,
相似三角形面积的比等于相似比的平方。
例:△ABC中,点D,E,F分别在边AB,AC,BC上, DE∥BC,EF∥AB, ,
求:
A
B
C
D
E
F
延伸:若DE∥BC,EF∥AB, ,
, .
(1)求y关于x的关系式。
(2)当x为何值时,y有最大值,
并求最大值。
(3)你认为 成立吗?为什么?
24.3.3相似三角形的性质
如图:△ABC和△A′B′C′是两个相似三角形,相似比为k,其中AD、A′D′分别为BC、B′C′边上的高,那么AD、A′D′之间有什么关系?
探究
∴
A’
B’
D’
C’
B
C
D
A
相似三角形对应高的比等于相似比.
证明: ∵△ABC∽△A’B’C’ ,
∴∠B=∠B’.
又∵∠ ADB=∠A’D’B’=
∴△ABD∽△A’B’D’.
相似三角形的性质
已知:如图,△ABC∽△A’B’C’,且相似比是K,
AD、A’D’为对应高.
求证:
.
思考:如图,△ABC和△A′B′C′相似,AD、A′D′分别为对应边上的中线,BE、B′E′分别为对应角的角平分线,那么它们之间有什么关系呢?
相似三角形的对应中线的比等于相似比.
相似三角形的对应角平分线的比等于相似比.
理论
相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.
性质1
相似三角形的性质
例1、点D,E,F分别为三角形ABC三边的中点,连结DE,AF,试猜想DE与AF有什么关系,并证明你的猜想.
A
B
C
D
E
F
证明:
连结DF、EF
∵AD=DB,BE=CE
∴DE∥AC
同理EF∥AB
∴四边形ADEF是平行四边形
∴DE、AF互相平分
运用
A
B
C
D
E
F
例2、点D,E,F分别为三角形ABC三边的中点,
O
重心
重心:三角形三条边上的中线
的交点
连结AD,BE,CF,交点为点O.
运用
结论1:三角形的重心与一边中点的连线
的长是对应中线长的三分之一
A
B
C
D
E
F
O
例4. 如图,点O为三角形ABC的重心,
猜想△AOB、 △ AOC、 △ BOC的
面积有怎样的关系?说明理由.
A
B
C
D
E
F
O
P
Q
结论2:三角形的重心与三角形三个顶点
组成的三个三角形的面积相等.
A
B
C
D
E
F
O
从而由等比性质有
相似三角形周长的比等于
相似比.
性质2
相似三角形的性质
性质证明
图中(1)、(2)、(3)分别是边长为1、2、3的等边三角形,它们都相似.
(2)与(1)的相似比=__________,
(2)与(1)的面积比=__________;
(3)与(1)的相似比=__________,
(3)与(1)的面积比=__________.
2:1
4:1
3:1
9:1
探究
已知:△ABC∽△A′B′C′,且相似比为k,AD、 A′D′分别是△ABC、△A′B′C′对应边BC、 B′C′上的高.
求证: .
证明:
∴
∴
∵ △ABC∽△A′B′C′,
性质3:相似三角形的面积比等于相似比的平方.
1.相似三角形对应边的比为0.4,那么相似比为______,对应角的角平分线的比为______,周长的比为______,面积的比为______.
2:5
2:5
2:5
4:25
演练
2. 已知△ABC∽△A’B’C’,且A’C’=3, BC=5,
AC=4,AB=7,则△A’B’C’的周长是 .
12
3. 已知△ABC∽△A’B’C’,
S△ABC:S△A’B’C’ =9:25, △ ABC的周长
是36,则△ ABC的周长是 .
60
4. 如图,在△ABC中,点D,E分别在AB,AC上,DE平行于BC,AD:DB=3:2,求四边形DBCE与△ADE的面积比.
解:∵DE∥BC
∴∠ADE=∠B ∠AED=∠C
∴△ADE∽△ABC
S△ADE:S△ABC=(AD:AB)2
∵AD:DB=3:2
∴AD:AB=3:5
∴S△ADE:S△ABC=9:25
∴S△ADE:S四边形DBCE=9:16
所以四边形DBCE与△ADE的面积比为16:9
5.如图,△ABC的边BC=12cm,高AD=6cm,边长为x
的正方形PQMN的一边在BC上,其余两个顶点
分别在AB、AC上.
(1)求x的值;
(2)求△APN与 △ABC
的面积比
B
Q
D
M
C
A
P
N
E
6. 如图,在梯形ABCD中,AB∥CD,
AC,BD相交于点E, S△DEC:S△CEB =1:2,
则S△DEC:S△BEA 等于 .
A
D
C
B
E
1:4
O
A1
A2
A3
A4
A
B
B1
B2
B3
1
4
7.如图,点
在射线
上,点
在射线
上,且
,
若
、
的面积分别为1,4,
则图中三个阴影三角形面积之和为 .
O
A1
A2
A3
A4
A
B
B1
B2
B3
1
4
10.5
课堂小结:
今天我们学习相似三角形哪些性质?
1、相似三角形对应高的比等于相似比,
相似三角形对应中线的比等于相似比,
相似三角形对应角平分线的比等于相似比。
2、相似三角形周长的比等于相似比,
相似三角形面积的比等于相似比的平方。
例:△ABC中,点D,E,F分别在边AB,AC,BC上, DE∥BC,EF∥AB, ,
求:
A
B
C
D
E
F
延伸:若DE∥BC,EF∥AB, ,
, .
(1)求y关于x的关系式。
(2)当x为何值时,y有最大值,
并求最大值。
(3)你认为 成立吗?为什么?
